同步阀瞬态响应的累计误差分析

费 烨，霍东东，杨 妍

（沈阳建筑大学 机械工程学院，辽宁 沈阳 110168）

同步阀又称分流集流阀，在液压系统多执行元件同步开环控制中得到广泛应用[1～2]。文献[3]通过对同步阀分流工况建模求解，发现两执行元件偏载压差、过阀流量均影响其同步精度，文献[4]对同步阀的静态分析得到了相类似结论。文献[5]对同步阀同步精度影响因素进行了仿真分析，文献[6]以体积最小、同步速度误差最小为目标对同步阀结构参数进行了优化。但上述研究多关注同步阀动态响应后的流量稳态误差，即执行元件的速度差，而同步阀作为有内部反馈机制的流量分配阀，其响应过程中出口流量对时间积分产生动态误差，导致两执行元件无法保证位置同步。文献[7]、[8]注意到了这一点，但并未给出定量研究。这种流量累计误差导致两执行元件位移差，使执行元件产生附加的形变应力，高压长行程时会造成结构损伤。因此，同步阀瞬态响应产生的位移误差应作为其基本性能参数加以重视而深入研究。

1 同步阀结构及工作原理

图1是拆解FJL-B15H型同步阀搭建三维模型后剖切得到的结构图，其结构左右对称，两侧弹簧使阀芯处于阀体中间位置，分流工况时换向活塞在远离对称中心线的图示位置。当压力油液p0、q0由P口进入，经阀芯径向孔和左右两侧固定阻尼孔分别变为p1、q1和p2、q2进入阀左右两腔，再经左右两腔中的可变节流口分别以液流p3、q1和p4、q2流入各自的执行元件。

图1 同步阀结构图

图2 同步阀工作原理简图

如图2所示，当负载压力p3=p4时，p1=p2，阀芯两侧受力平衡，阀芯无移动，左右两侧可变节流孔开度不变，q1=q2；若p3＞p4，据小孔流量公式：q=CAΔpφ有：q1＜q2，p1＞p2，左侧弹簧腔压力大于右侧，阀芯右移使左侧可变节流孔开度增大，而右侧可变节流孔开度减小，导致q1变大、q2减小，直至q1=q2、p1=p2，阀芯重新恢复平衡，两执行元件运动速度同步。同理，若p1＜p2，阀芯左侧，调节流量相等。集流工况此相似，仅进油口与出油口相反。

2 同步阀建模

2.1 同步阀AMESim仿真模型

根据同步阀结构和工作原理，利用AMESim中HCD库的质量、固定阻尼孔、可变阻尼孔、容积及活塞等单元搭建出同步阀模型如图3所示。

图3 同步阀仿真模型

利用该阀Solidworks三维模型，测量和计算仿真模型中相关参数如表1所示。

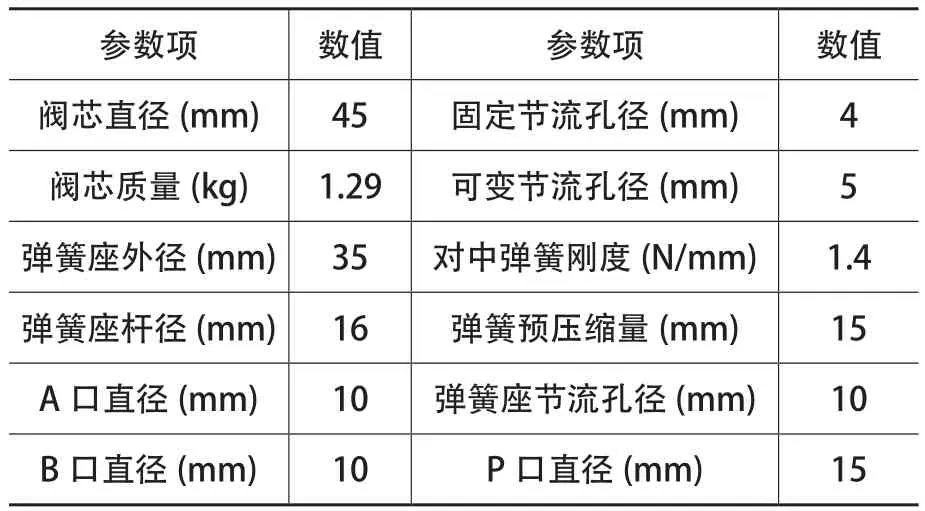
表1 同步阀结构参数

2.2 仿真模型验证

为验证所建同步阀模型，可将其置入双缸同步回路，通过两油缸所分配的流量进行验证。将同步阀模型与元件库中液压泵、液压缸和信号源等元件连接，搭建出双缸同步回路AMESim模型如图4所示，其中油缸内径160mm、活塞杆直径140mm。

该同步阀样本提供的性能参数见表2，即额定流量63L/min下进行分流，当双缸无杆腔压差分别为0MPa、6.3MPa、20MPa、30MPa时，其速度同步精度σR与偏载压差Δp应满足表2要求。

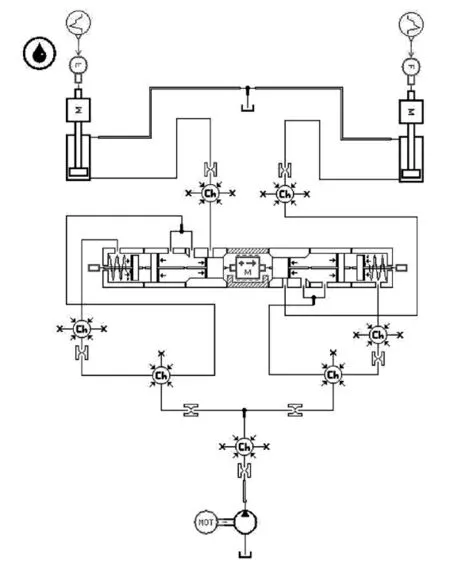
图4 同步阀分流工况AMESim仿真模型

表2 同步阀样本分流工况同步精度

设置验证工况为：泵输出同步阀额定流量63L/min，同步阀A、B口偏载压差在0～2s间保持为0，2s开始分别阶跃变为PA＞PB前提下的6.3MPa、20MPa、30MPa。

设置仿真时间5s，时间间隔0.01s，得到不同偏载工况下阀芯位移曲线，如图5所示。

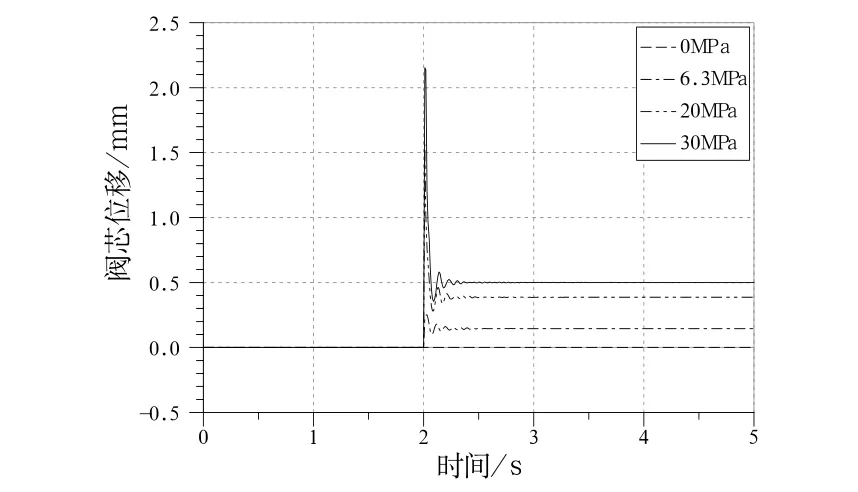
图5 不同偏载工况下阀芯位移曲线

图5的曲线族表明，同步阀阀芯位移对负载压差的响应为典型二阶系统，这与文献[8]的理论分析结果相一致；当偏载0MPa时阀芯不动，偏载增加阀芯位移随之变大表明阀芯右移，同步阀左侧可变节流孔开度增加而右侧可变节流孔开度减小。因此仿真模型响应曲线趋势正确。

图6是偏载30MPa时A、B口流量曲线，由此可得不同压差条件下，同步阀稳定工作时A、B口流量差（表3）。

图6 偏载30MPa工况下A、B口流量曲线

表3 样本工况下同步阀A、B分流口仿真流量差

表4 不同偏载差压下同步阀仿真同步精度

3 同步阀同步性能仿真分析

3.1 同步性能仿真

借助图4回路仿真模型，对该同步阀同步精度进行分析。

在前述模型验证工况仿真结果中提取偏载30MPa时的双缸位移曲线如图7所示。

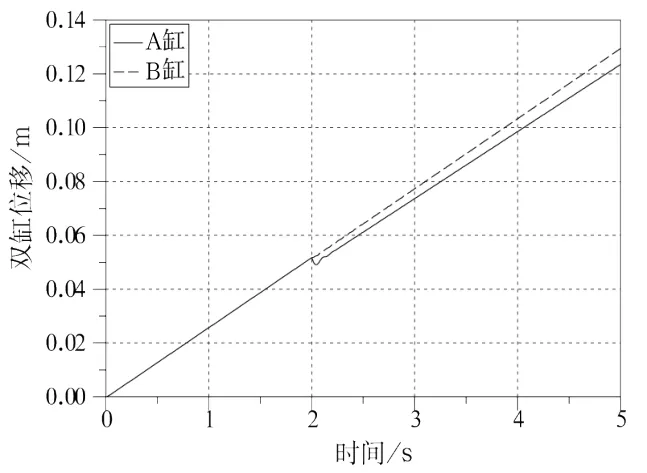
图7 偏载30MPa工况下双缸行程曲线

图7表明：2s前两缸负载相同，其速度、位移均同步，2s开始阶跃偏载经动态响应后两缸位移曲线不再重合也不平行但斜率偏差很小，说明偏载响应后双缸失去位置同步，也不再保持严格的速度同步。原因在于图6所示同步阀A、B两口流入两缸的流量差，在阶跃偏载后既存在瞬态误差也存在稳态误差。稳态误差对同步阀同步性影响已有相关文献研究，本文不再赘述。这里主要考虑瞬态响应过程中的流量误差对其同步精度的影响。考虑同步阀瞬态过程双缸流量的时变特性，本文提出时均瞬态累计误差概念对其进行研究。

3.2 时均瞬态累积误差

所谓时均瞬态累计误差是指同步阀瞬态响应过程中两分流口单位时间时变流量之差，可记为

式中，T为瞬态响应的调整时间。

由图6可知偏载30MPa时A、B口流量曲线瞬态响应调整时间TA＜TB，取B口稳定工作流量±5%，得TB=0.34s。对A、B口流量曲线作差得到流量差曲线，再利用AMESim中曲线积分求解功能对流量差积分，根据时均瞬态累计误差公式，计算30MPa偏载下同步阀时均瞬态累计误差。同理可得其他工况时均瞬态累计误差（表5）。

表5 不同偏载下同步阀A、B口时均瞬态累计误差

由表5可知，系统偏载30MPa时，瞬态响应导致的双缸位移差2.315mm，这对高精度控制应属很大的绝对误差。因此，瞬态响应过程对同步阀同步精度有明显影响，其瞬态累计误差应考虑在对同步阀同步性影响之内，不可忽略。

3.3 时均瞬态累计误差影响因素分析

选取同步阀独立的结构参数：固定节流孔直径、可变节流孔初始直径、弹簧刚度，以及使用参数：进口流量、偏载压差，通过仿真分析其变化时对同步阀时均瞬态累积误差的影响。

将固定节流孔直径以步长0.1mm从3.5mm离散至4.5mm、可变节流孔直径以步长0.1mm从4.5mm离散至5.5mm、弹簧刚度以步长0.5N/mm从0.4N/mm离散至3.4N/mm，P口流量以步长1L/min从55L/min离散至65L/min、双缸偏载压差以步长5MPa从5MPa离散至35MPa，其它未作说明的均取偏载30MPa时测试工况参数。分别经批处理得到时均瞬态累计误差随上述因素变化的曲线，这里给出较为典型的曲线，如图8～图10所示。

从所获仿真曲线看，时均瞬态累计误差随固定节流孔直径增加呈抛物线上升趋势，随可变节流孔初始直径和偏载压差的增加呈线性递增规律，随弹簧刚度和P口流量的增加呈线性递减变化。

因此，从降低时均瞬态累计误差的角度看，设计时同步阀应尽可能减小固定节流孔直径、可变节流孔初始直径，增加弹簧刚度；使用时则应减小偏载压差、增大同步阀进口流量。但减小固定节流孔和可变节流孔直径在大流量分流工况下会增大压力损失而降低系统效率，特别是加大弹簧刚度更与降低同步阀稳态误差的要求相矛盾[5]。

4 结 语

通过对同步阀控制的同步回路建模和仿真分析，发现同步阀输出流量的瞬态响应误差对同步回路的同步性影响明显。考虑到瞬态过程流量的时变性，提出同步阀时均瞬态累计误差的概念对这种影响加以研究，并得到如下结论：①在同步阀额定流量下，其时均瞬态累计误差随偏载压差的增加呈抛物线趋势递增，生产厂家应将其作为基本性能参数指标在样本中加以标示；②固定节流孔直径、可变节流孔初始直径和弹簧刚度等结构参数对同步阀时均瞬态累积误差有明显影响，设计时应综合考虑过阀压力损失和稳态误差优化确定；③从使用角度看，选用的同步阀实际流量应尽可能接近其额定值，且应尽可能减小偏载。

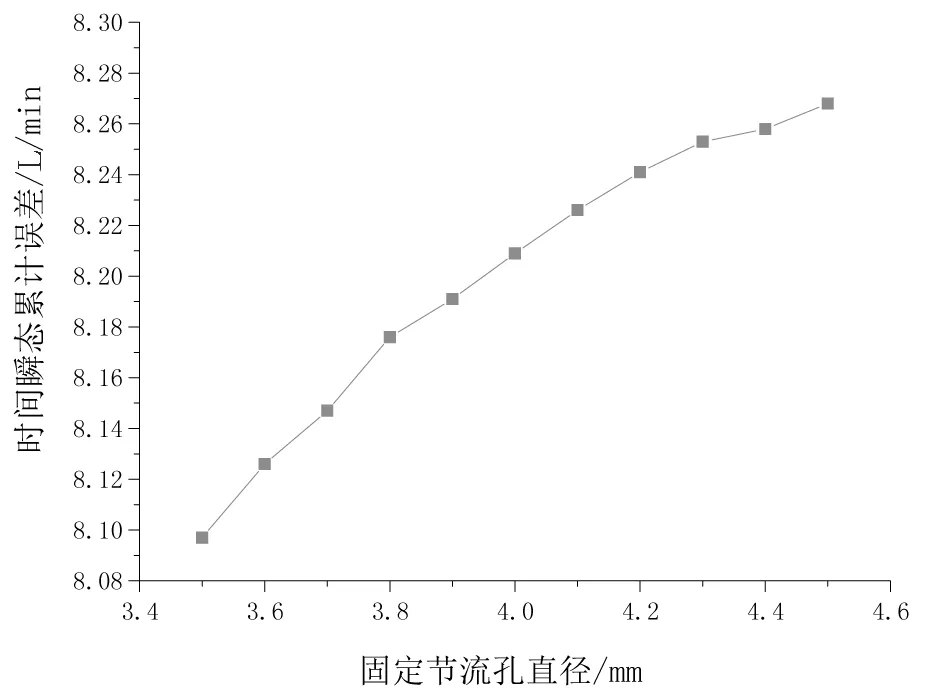
图8 固定节流孔直径对时均瞬态累计误差影响

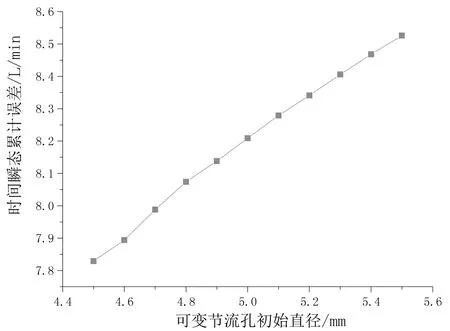
图9 可变节流孔初始直径对时均瞬态累计误差影响

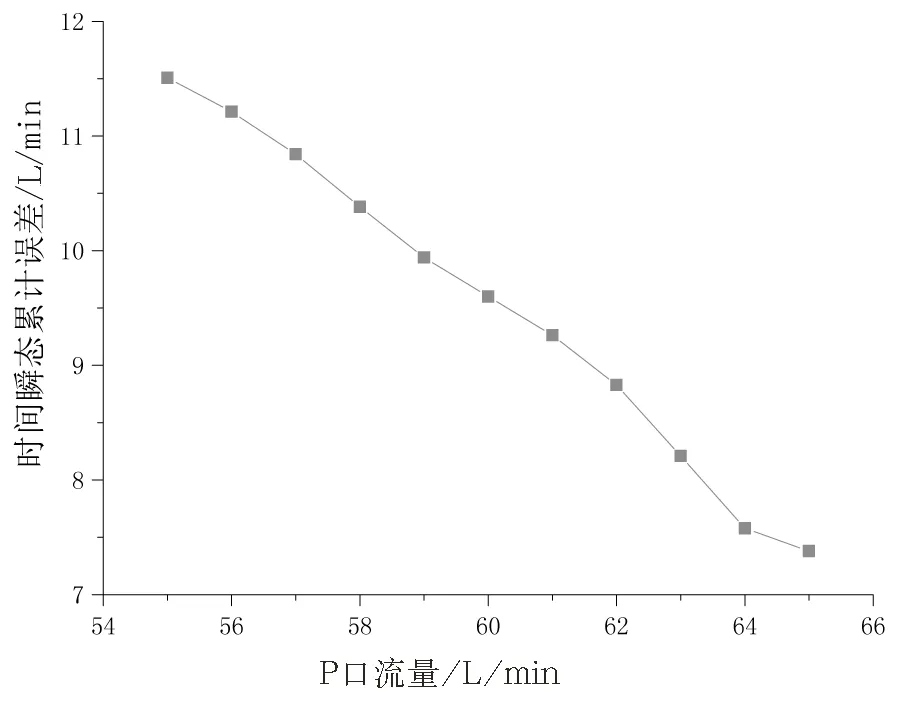
图10 P口流量对时均瞬态累计误差影响