宝鸡峡灌区农业供水效益C-D函数岭回归分析
2019-01-09高志玥李怀恩贾斌凯田若谷
高志玥,李怀恩,张 倩,成 波,贾斌凯,田若谷
(1.省部共建西北旱区生态水利国家重点实验室(西安理工大学),陕西 西安 710048; 2黄河水利委员会上游水文水资源局,甘肃 兰州 730000)
渭河是陕西省的主要水源之一,在承担沿河城市工、农业供水重要任务的同时,还具有泄洪纳污、保持生态平衡、提供宜居环境的生态功能,发挥河流的生态功能需要在社会经济发展的同时保障河道生态基流,协调区域经济用水与河道生态用水。农业作为流域的用水大户,现行的农业供水价格仅能体现农业供水的生产成本与管理经营费用[1],而难以体现水资源的真实效用,不能准确评价水资源作为国民经济可持续发展重要基础资源在自然生态系统、社会经济系统中所发挥的重要作用,使得区域水资源保护工作受到限制。
为了合理计算社会生产供水效益,相关研究借助C-D生产函数(the Cobb-Douglas production function),将社会生产中的“水量投入”列为生产函数变量之一,通过拟合水资源投入与资本、劳动力投入和产出之间的关系,求解水资源要素变动的边际产出效应,该方法符合社会生产实际,多年系列数据较容易获得,可为水资源合理配置提供更为合理的依据。目前,进行供水效益分析的C-D生产函数,多是在原函数“资本”和“劳动”变量基础之上加入“水资源”变量进行计算,例如龚园喜[2]以Solow改进的C-D生产函数为基础,计算浙江省GDP、工业、农业供水效益,分析了水资源的经济效益;胡金杰等[3]建立改进了的C-D生产函数模型,计算了太湖下游地区苏州市的GDP单位供水价值。为支持生物燃料发展的成本效益分析,2016年Kaenchan P等[4]采用边际效益原理对泰国的三种经济作物木薯、甘蔗和油棕榈进行供水效益分析,结果显示扣除了0.2泰铢的外部成本,它们的单方水净效益分别在1.5~6.7、0.9~4.8和0.6~2.6泰铢之间,首次以货币单位对木薯、甘蔗和油棕榈栽培中的用水效益与费用进行了研究。这种简单的包含水资源投入的C-D生产函数,可用来简单估算区域经济发展中水资源所做的贡献,但是以函数现有资本、劳动要素添加水资源要素分析,具体到某一生产领域(比如粮食生产或林业生产)估算供水效益内容不够充实,结果不够精确,因为各生产领域所投入的要素各具有其特殊性。近期,盖美等[5]基于边际效益理论选取除劳动力与农用机械总动力外的降水量、化肥使用量、有效灌溉面积以及政府影响力等指标作为C-D生产函数的解释变量,将农业用水边际效益作为被解释变量,采用双对数回归方程,逐步回归分析了辽宁沿海经济带生产用水的边际效益,在要素选择和回归方式上有所改进。回归分析方法在农业、经济等领域的应用最为广泛,以上研究所采用的模型多为一般的多元线性回归模型,因投入要素较少,要素间近似的线性关系有可能被忽视,当投入要素增加,自变量间严重的多重共线性会使得估计的稳定性变差、精确性降低,无法得到合理的经济解释,若仍采用一般最小二乘估计进行回归分析,会降低模型的应用价值。为了使所建立的模型更符合农业生产实际,本文拟采用岭回归分析,针对农业生产的特殊性扩充并修改索罗C-D生产函数:将灌溉用水作为投入要素之一,在传统要素基础上增加化肥与耕地投入丰富模型内容,同时为避免要素间重复核算,用农耕机械总动力代替固定资本投资作为生产函数解释变量,建立生产函数模型;为准确估算农业供水效益,选取代表农业生产最终劳动成果的“农业增加值”而非“农业总产值”作为生产函数被解释变量进行回归分析,避免了地区农业生产过程中消耗的各种物质产品价值的重复计算。
近年来随着国家生态文明建设工作的推进,关于河道生态基流量及其功能价值研究已取得了一定的研究成果,“绿水青山就是金山银山”的理念已深入人心,然而现阶段河道生态基流保障研究仍处于起步阶段,基流的合理保障水平需要明确的损益对比分析。宝鸡峡灌区地处渭河上游,引水灌溉直接影响渭河干流水量,上游水量不足使得中游水体自净能力受限,连带下游河道淤积;然而宝鸡峡灌区是关中最大灌区,对区域粮食安全、经济发展有重大贡献,枯水期农业用水与河道生态基流需水矛盾突出,减少农业供水保障河道生态基流会对农业生产造成直接的经济损失和间接的社会影响,在铁腕治污进入“新常态”的社会背景下,采用经济手段协调生产用水与生态用水,对农业缺水损失实施生态补偿是目前现实可行的办法,这使得合理评价农业供水的经济效益显得尤为重要。按照“谁受益、谁补偿”的补偿原则,首先需要对宝鸡峡灌区农业供水效益进行合理的分析计算,进而分析保障生态基流可能造成的直接经济损失,为渭河河道生态基流保障补偿研究提供科学依据,对缺水地区水资源配置与保护工作具有实际的指导意义。
1 研究区域和研究方法
1.1 宝鸡峡灌区简介
宝鸡峡灌区位于陕西省关中平原西部,西起宝鸡市以西的渭河峡谷,东至泾阳,南临渭水,北抵渭北高原腹地,灌溉着宝鸡、杨凌、咸阳、西安的14个县(市、区)、97个乡镇的近20万hm2农田,总控制面积2 355 km2,有效灌溉面积1 883 km2,是一个两处枢纽、引抽并举、渠库结合、长距输水、水工门类齐全的大型灌排体系,是陕西省目前最大的灌区。灌区以占全省1/18的耕地面积,生产了占全省总产量1/7的粮食和1/4的商品粮,被誉为“三秦第一大粮仓”[6]。灌区农作物以小麦、玉米为主,2015年农业增加值372亿元,占比超过整个关中地区的50%,占整个陕西省的31.6%;灌区渠首多年平均年引水量[7]为5.3亿m3,根据渭河林家村(合)站2015年实测流量,渭河天然来水量9.44亿m3,灌区引水后河道剩余水量4.7亿m3(林家村三站),年内仅有4个月能满足8m3/s的生态基础流量[8],基流缺水量达1.16亿m3,社会生产用水与生态基流需水间矛盾突出。
为了在保障河道生态基流的基础之上维持区域经济可持续发展,需要分析保障基流可能造成的各种经济损失与社会影响,进行基流保障的补偿研究,而这一切都建立在区域水资源供水效益合理计算的基础上。
1.2 研究方法
Cobb-Dauglas生产函数的基本形式如下:
Q=A·Kα·Lβ
(1)
其中,A为效率系数,独立于其它要素之外的不变参数;K,L为资本、劳动投入;α,β为资本、劳动力产出弹性,0≤α≤1,0≤β≤1,α+β大于1、等于1、小于1分别表示规模报酬递增、不变和递减。
然而在实际研究过程中,生产函数的应用经常以时间序列数据为样本,即在时间序列上取多个截面,在这些截面上同时选取多个样本观测值进行研究,而技术的发展恰恰与时间密不可分,这使得面板数据关于“技术进步的作用在所有样本点上都是相同的”基本假定与实际不符;更有人对α+β=1的函数形式提出异议,这些使得原始的生产函数在实际应用中受到限制。
1957年,Solow改进了C-D生产函数,假定技术进步未具体体现在固定资本和劳动中,引入了时间函数A(t)代替效率系数A,在生产函数中加入时间指数趋势以测定技术进步,将A(t)的形式假设为A0(1+λ)t,λ是技术进步系数;t表示年份系列,其形式如下:

(2)
Solow改进的C-D生产函数模型弥补了技术进步测定的遗憾,能够很好地描述资本、劳动投入等要素和技术进步对经济增长的贡献。结合本文的研究目的,在原函数基础上对农业生产投入要素加以扩充,以更加精确地计算农业供水效益。
农业生产是自然再生产与经济再生产的结合,生产过程必然受到自然条件、技术条件和各种经济因素的制约和影响[9-10],本文选取生产化肥投入(Fertilizer-F)、农耕劳动力投入(Labour-L)、耕地资源投入(Plowland-P)、农业机械投入(Machinery-M)以及水资源投入(Water-W),作为函数解释变量,改写生产函数形式如下:
Y=ft,F,L,P,M,W
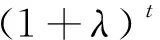
(3)
其中,Y为农业产出;A0为常数;t为年份序列;λ为技术进步系数;α为化肥产出弹性;β为劳动力产出弹性;ε为耕地产出弹性;θ为机械产出弹性;γ为水资源产出弹性。
这样就确立了包含水资源投入在内的多投入要素的农业C-D生产函数。弹性分析可以明确表示各种要素对国民产出的影响程度,所以可以利用弹性系数求得水资源对各产业的边际效益。将(3)式线性化后求W的偏导数就可以确定单位农业产出的边际效益BW[11]:
(4)
弹性是因变量的相对变化与自变量相对变化的比值[12],其绝对值大小可显示出经济因变量相对变动对经济自变量相对变动的反映程度,其符号的正负可反映出水资源投入量追加时对经济增长影响的趋势,计算效益时取其绝对值[13]。
多元线性回归模型多条经典假设中,最重要的一条是解释变量之间互不相关[14-16],即X1,X2,…,Xn不存在线性关系,因为普通最小二乘估计要求解释变量矩阵X为列满秩矩阵,即XTX为非奇异矩阵,此时回归系数向量β有唯一解:
(5)
然而在实际的统计数据中,由于解释变量之间本身存在着各种各样的联系,比如:耕地面积与灌溉水量、化肥使用量;劳动力与劳动对象等,因此要充分考虑解释变量可能存在的多重共线问题。当多重共线存在时,|XTX|≈0,(XTX)-1不存在,无法得到有效的估计系数,模型预测没有意义。
克服多重共线问题可采用岭回归分析[17],岭回归(ridge regression)即在|XTX|≈0时设想给矩阵XTX加上一个正常数矩阵KI(K>0,I为单位矩阵),使得矩阵XTX+KI较矩阵XTX接近奇异的程度大幅减小,其中K称为岭参数或岭参数,β的岭回归估计为:
(6)
关于岭参数K的选择学界一直有诸多讨论,以现在的科学水平来看主要采取岭迹图来分析[18-19]。由于岭回归是有偏估计,K的选择应遵循以下原则[20]:在各回归系数的岭估计基本趋于稳定的同时使K值尽量的小;所得的回归系数符号较最小二乘回归系数更为合理且没有不合乎经济意义的绝对值等。岭回归放弃了最小二乘法的无偏性,获得了比无偏估计更稳定、更加符合实际的回归系数,对病态数据的拟合要强于最小二乘法。
2 农业生产函数模型建立
2.1 数据说明
宝鸡峡灌区所辖区域,包括宝鸡、杨凌、咸阳、西安的14个县97个乡镇,但在西安市仅有高陵一个乡镇,有效灌溉面积约占全灌区的0.5%,相关统计数据不易获取;杨凌是中国第一个农业高新技术产业示范区,经济总量较小,新中国成立后行政隶属关系变化频繁,2008年8月国务院批准将宝鸡市扶风揉谷乡划归杨凌,为研究方便,将杨凌示范区相关数据与宝鸡市合并处理,统一分析。根据农业生产数据的易获取性,仅选取宝鸡市、咸阳市两市的农业生产数据进行回归分析,计算农业水资源弹性系数进而分析宝鸡峡灌区所在行政区(宝鸡市、咸阳市)农业供水效益,灌区总供水效益则根据灌区及灌区所在行政区有效灌溉面积之比计算。
用统计学的方法进行回归分析,为使估计值精确可信,希望统计数据系列尽量的长,但是随着时代变化,统计年鉴数据为适应社会需要会做出相应调整,比如“农林牧渔业产值”这一统计量在2004年以前的核算范围修改了五次之多,2004年至今其统计数据取消了农民家庭兼营性工业,同时把农林牧渔服务业纳入核算范围;“农业用水量”也是同样,2004年之前的统计数据没有区分农业用水与林牧渔业用水,因此为了数据间对应投入产出关系的一致性, 选取2004-2015年的农业生产数据进行多元回归分析,投入要素包括化肥施用折纯量Fertilizer(F,万t)、农业从业人员Labour(L,万人)、作物总播种面积Plowland(P,万m2)、农用机械总动力Machinery(M,万kW)以及农业灌溉水量Water(W,亿m3)。产出选择农业增加值Y,该值扣除了农业生产过程中物质产品的中间消耗,没有重复计算,可作为函数的被解释变量。以上数据均来自《陕西省统计年鉴》对各市(区)逐年的统计数据,用水量数据来自《陕西省水利统计年鉴》。
2.2 拟合结果
利用SPSS 19.0对宝鸡市、咸阳市的农业数据进行多元线性回归分析,模型拟合良好,但变量t检验不显著,方差扩大因子VIF≥10,经共线性诊断发现,各要素的条件指数都很大,且系数矩阵方差比例大多<0.5,自变量之间存在着严重的多重共线性。
采用岭回归分析进行修正,对包括时间变量在内的6个解释变量做岭回归分析,设置岭参数K在[0,1]之间变化,每次增加步长0.02,绘制的估计值绘制关于K的岭迹图,见图1。
如图1所示随着岭参数K的增大,宝鸡市的时间变量T迅速下降,农耕机械总动力M迅速上升,化肥折纯量F与耕地P在微小跳动后逐渐下降并较快趋于平稳,劳动力L未见较大变化,灌溉供水量W由负转正呈逐渐上升趋势,在K=0.4附近各变量趋于稳定;咸阳市的时间变量T迅速下降,化肥变量F没有大的变化,劳动力变量L迅速下降并由正转负,农耕机械变量M迅速上升并由负转正,耕地P、灌溉供水量W缓慢上升后趋于平稳,在K=0.2附近各变量趋于稳定。据此分别在K=0.4、K=0.2处建立农业生产函数模型:

(7)

(8)
两方程决定系数分别为0.968、0.979,F检验值分别为25.0、39.4,统计学意义概率P(sigF)均<0.05,回归效果良好,方程具有统计学意义,各解释变量的回归系数、偏回归系数显著性检验见表1。

图1 宝鸡市(a)、咸阳市(b)农业要素回归系数岭迹图Fig.1 Ridge trace of regression coefficient from agricultural input factors

农业变量Agricultural variables宝鸡市 Baoji Cityβ*P valueK=0K=0.40SE(B)K=0K=0.40咸阳市 Xianyang Cityβ*P valueK=0K=0.20SE(B)K=0K=0.20时间 Time0.2450.0100.0010.0310.0060.3080.0080.0010.0380.007化肥折纯量 Fertilizer0.2190.1900.0030.5280.1190.1950.0400.0310.1070.119劳动力 Labour-0.0630.3010.3330.7100.687-0.0760.2400.2081.4950.586耕地 Plowland-0.1140.9350.0631.0090.550-0.1140.1510.0962.0780.953机械总动力 Machinery0.2110.9410.00050.7370.0550.2610.3250.0030.5660.117灌溉供水 Water0.0980.3510.0720.7920.2380.0750.4870.2510.3200.361常数 Constant00.0100.00562.013.680.0000.0080.00773.518.4F值F25.0SigF0.00141F39.4SigF0.00047
注:*β-岭估计的标准化回归系数;K=0时即为最小二乘估计;SE(B)-回归系数标准误差。
Note: *β-The normalized regression coefficient of ridge regression analysis; SE(B)-Standard error of regression coefficient.
偏回归系数显著性检验显示,经岭回归分析修正后,模型概率P值明显减小,就灌溉用水变量W来看,宝鸡市由0.351降低为0.072;咸阳市由0.487降低为0.251,显著性水平均有不同程度的提高。
3 宝鸡峡灌区农业供水效益分析
3.1 农业供水效益计算
在模型建立的基础上,根据式(4)可计算宝鸡峡灌区各市的农业供水效益,从生产函数可以看出,宝鸡、咸阳的水资源产出弹性的绝对值分别为0.098、0.075,就经济意义而言,农业增加值每增长1%,水资源在其中的贡献率分别为0.098%、0.075%。以2015年为例,宝鸡市农业增加值104亿元,农业灌水量4.47亿m3,单方水产出率为23.2元·m-3,按水资源贡献占比9.8%计算,供水效益为2.29元·m-3;咸阳市农业增加值269亿元,农灌水量6.01亿m3,单方水产出率为44.7元·m-3,按水资源贡献占比7.5%计算,供水效益为3.34元·m-3,两市农业供水效益年际变化过程见图2,图中“平均值”曲线,即灌区所在行政区农业供水效益的均值变化过程。
从图2可以看出:两市农业供水效益均呈逐年递增趋势,从2004年的0.739元·m-3增加到2015年的2.89元·m-3,12年间增长了2.15元·m-3,其中宝鸡增长1.65元·m-3、咸阳增长2.53元·m-3。可见,农业供水效益随时间变化的同时,也存在空间差异。
图3所示为剥离技术进步影响的农业要素分摊比重,可见水作为纯粹的资源性投入,对农业生产最终成果的分摊比重宝鸡市(13.98%)大于咸阳市(10.36%),但其供水效益宝鸡市低于咸阳市,从供水效益分摊的对象来看,咸阳市的农业增加值均值是宝鸡市的2.64倍,农业单方水产出率均值是宝鸡的1.67倍,农业经济总量的巨大差异,奠定了农业供水效益的差异,而两市农业经济总量差异主要源自两地农耕灌溉技术水平与作物种植结构差异。
从农耕灌溉技术水平来看,咸阳市技术进步系数(0.36)λ大于宝鸡市(0.278),其技术的年进步速度要快于宝鸡市,对咸阳市农业增产贡献较大;12年来两市常用耕地面积(宝鸡3 091 km2、咸阳3 579 km2)差异不大,但宝鸡市内有效灌溉面积不到咸阳市的70%,仅1 601 km2,如图4所示宝鸡市作物历年最大产量为436万t,仅为咸阳的36%,有效灌溉面积差异造成作物产量的差距。
从作物种植结构来看,宝鸡峡灌区北部多为经济效益高、灌溉定额小的果园,且多分布于咸阳市礼泉县、乾县南部和兴平县北部;武功县以东至兴平市以西大面积种植菜地[21]。如图5所示,宝鸡市2015年的粮食作物产量占总产量的34.3%,而同年咸阳市仅占15.9%;粮经产量比宝鸡为23∶44、咸阳为7∶37,粮食作物的灌溉定额较高,经济效益却远不如果蔬类作物,可见无论是粮食作物总量比或是粮经比,咸阳市作物的种植结构都优于宝鸡市。

图3 农业投入要素弹性系数所占比重Fig.3 Proportion of elastic coefficient of agricultural input factor

图4 宝鸡峡灌区所在行政区农作物产量年际变化Fig.4 Annual changes of crop yields in the administrativeof the Baoji Gorge Irrigation District

图5 宝鸡峡灌区所在行政区粮食作物产量占比年际变化Fig.5 Annual changes of the percentage of cereal yields inadministrative of the Baoji Gorge Irrigation District
宝鸡峡灌区的农业供水总效益需要根据灌区及所在行政区有效灌溉面积,按面积比拟法计算。
灌区农业供水总效益=ω·∑行政区农业供水总效益
(9)
(10)
宝鸡峡灌区有效灌溉面积1 883 km2;根据《陕西省统计年鉴》2010-2015年统计数据,宝鸡、咸阳两市有效灌溉面积多年均值分别为1 601 km2、2 295 km2,合计3 897 km2,经计算ω=0.483。供水效益历年情况如表2所示,农业供水总效益逐年递增。分析原因,一方面由于全球气候变暖,使得降水量减少、蒸发量增加,主要作物冬小麦、夏玉米、果树、油菜、棉花等的需水量显著增多[22],使得12年间农业供水总量有所增加;另一方面由于技术进步、政策机制保障、农田水利建设投入、农业生产投入等人为因素作用,在一定程度上缓解了气候变暖对农业供水和农业生产带来的负面影响,作物种植面积的减少与“粮经比”的降低在农业需水量逐年递增的背景下,取得了显著的节水增产效益[23]。
3.2 合理性分析
方法内对比:王珍[24]等采用陕西省2005-2010年统计数据,选取劳动力、资本、水资源作为C-D生产函数的投入要素对渭河陕西段河道供水价值进行了分析,其GDP用水弹性为0.313,不考虑地域差异,研究内容具体到农业并增加与之相关的投入要素,水资源弹性系数明显减少,更能真实体现灌溉对农业生产的贡献;由于模型的建立过程实质上是抽取样本对总体进行估计,在保证要素间投入产出关系对应的同时,应尽量延长样本系列年限以增加模型精度。
方法间对比:成波[25]等采用能值法研究了渭河关中段的农业供水效益,该方法是以太阳能值为统一度量标准,在明确农业生产过程的能量、物质投入后,按要素能值占总能值的比例计算其效益分摊系数,进而对供水效益进行分摊计算,结果显示由于农机、化肥等人为投入元素能值占总能值比例逐年递增,使得水资源投入在农业生产过程中的地位有所下降,关中各市农业供水效益分摊系数呈逐年递减趋势,但供水效益逐年递增。若将本文所用农业要素与农业增加值数据进行归一化处理,消除原始数据量纲和数量级差异,即Xij用Xij/Xmax-ij代替,其中Xmax-ij为j要素历年最大值,我们可以在同一坐标轴上得到各要素投入与农业增加值历年变化情况(见图6)。
从图中可见,两市的规模指数(∑Xj)在逐年增大,这表示两市农业生产规模在逐年递增;化肥F和农耕机械M投入与农业增加值有明显的同增长趋势;耕地P与劳动力L投入历年均相对稳定;宝鸡市的农业灌溉供水量W随生产规模逐年增长,而咸阳市则是先增长后下降,呈现出明显的节水增产效果。正如本文图3所示,化肥F与M投入对农业生产成果的分摊比重最大,两市合计均超过60%,对灌区农业增产增收影响显著,而灌溉供水量W、耕地P与劳动力L投入次之。即农业供水单方水产出率(Y/W)逐年递增是农耕技术改进、种植结构优化的结果,这正是农业供水效益逐年递增的基础。
与现行水价对比:水利工程供水价格由供水生产成本、费用、利润和税金构成,农业用水价格按补偿供水生产成本、费用的原则核定,不计利润和税金,关中地区现行农业水价大部分是2004年进行的水价调整[1],宝鸡峡灌区终端水价约0.245元·m-3,2009年经省物价局、水利厅核算,灌区合理水价[26]应为1.32元·m-3,与本文计算成果1.23元·m-3相差不大,计算结果合理。
4 结论与展望
隶属于计量经济学领域的C-D生产函数是以社会生产的投入产出关系为基础,利用统计学原理找寻社会生产的内在规律,本文根据宝鸡峡灌区所在行政区的农业经济数据,采用有偏估计的岭回归分析消除多重共线影响,建立农业C-D生产函数,计算了灌区农业供水效益,结果显示12年间宝鸡峡灌区的农业供水呈逐年递增趋势,主要原因在于农耕灌溉技术水平进步和灌区作物种植结构优化。改革开放以来,农耕机械替代手工劳动力成为农业生产的主要力量,先进的节水灌溉技术逐步替代了土渠输水、大水漫灌的传统灌溉方式,农耕技术进步使得单位面积灌溉定额逐年减小,有效灌溉面积却逐年递增;在粮食作物产量稳定的前提下,“粮经比”逐年递减使得灌区农业经济总量逐年递增。这就使得以农业增加值为效益分摊对象的农业供水效益逐年递增,供水效益从0.739元·m-3增加到2.89元·m-3,总供水效益从3.09亿元增加到14.6亿元。

表2 宝鸡峡灌区2004-2015年农业灌溉供水效益与总效益
注:*由于缺少宝鸡峡灌区历年农业供水数据,灌区农业供水效益仅以宝鸡、咸阳两市均值代表。
Note: *For the lack of irrigation water data in Baoji Gorge Irrigation District, the benefits of water supply in the irrigation area is represented by the mean of Baoji and Xianyang.

图6 农业生产数据年际变化趋势图Fig.6 Annual strend of agricultural production data
农业是人民生活的保障,是社会生产的用水大户,具有极大的节水潜力,仅以现行水价评价农业供水效益显然有失合理性。本文仅选取农业相关要素进行回归分析,排除了林牧渔业干扰,充分考虑到保障河道生态基流取水的生态性、现实性和可行性,为基流保障直接经济损失计算提供了可靠依据。另外,在河道生态基流保障损失分析的基础之上,结合前人对基流价值的研究成果,可分析生态基流不同保障水平下“价值”与“损失”的关系,进一步研究不同条件下生态基流的合理保障水平,为渭河河道生态基流保障工作提供科学依据,同时可为缺水地区水资源配置研究提供参考。
