基于SFA的我国农业生产效率测算及区域性差异分析

韩振兴， 刘东辉， 常向阳

(1.山西农业大学经济管理学院，山西太谷 030801； 2.南京农业大学经济管理学院，江苏南京 210095)

改革开放以来，我国农业生产表现出快速增长态势，但是随着生产要素价格的上升和资源约束问题的日益凸显，农业生产依靠增加要素投入来增进产量的方式不再能持续为继，新的农业发展方式必须依靠促进农业技术进步、提高效率来实现。

经济增长的2个来源是要素投入和全要素生产率(total factor productivity，简称TFP)增进，而TFP增进的途径又有2个：一是微观主体自身TFP的增长，二是资源配置效应。微观主体的TFP增进主要依靠技术进步和技术效率的提高，其中：技术进步主要表现为生产前沿面的移动，是农业生产长期进步的主要动力来源；技术效率表示实际产出和生产前沿面上可能的最大产出的距离，反映的是农业生产短期进步的主要来源。资源的配置效率是反映现有配置方式对资源的利用程度及改进空间，其计算需要要素价格指标，因为价格数据的不完整，本研究暂不分析配置效率，在后续的研究中会弥补这一部分的不足。在实际中，技术进步主要通过技术发明、技术创新等方式来实现，技术效率主要通过制度创新、技术扩散等方式来消除或降低技术效率提高的限制因素。

本研究选取1990—2012年我国主要农业生产大省13个省的面板数据，利用随机前沿生产函数(stochastic frontier aproach，简称SFA)来测算我国农业生产效率，并分析23年间13个省农业增长的动力及其影响因素，同时分析了技术进步和技术效率在我国农业增长中的区域性差异，针对性地提出了发展措施和政策建议。

1 相关研究述评

农业增长的源泉主要有增加要素投入和TFP增进，TFP增进又可分解为技术角度和要素配置角度，技术角度主要是指技术进步和技术效率2个方面。从技术角度来看，造成TFP差异的主要原因是研究主体吸收先进技术的速度差异和使用先进技术的效率不同，Nelson等认为是吸收先进技术的速度不同[1-3]：Fare等认为是使用先进技术的效率不同[4-8]。

在研究我国农业全要素生产率增长变化的文献中，陈卫平等认为我国农业TFP增长主要来自技术进步[9-13]；车维汉等认为技术效率的作用更为显著[14-15]；匡远凤认为技术效率阻碍了我国农业增长，除此之外的因素均促进了我国农业TFP的增长[16]；黄金波等认为TFP对我国粮食生产增加的作用和贡献有限，其主要动力在于要素投入的增加，但技术效率的正向增长，对TFP起到了正向作用[17]。上述学者的一致观点在于我国农业增长同时存在技术进步和技术效率损失2种情况，分歧在于二者的作用大小不同。

分析我国农业增长区域性差异的文献主要有李谷成认为我国各省农业TFP的增长具有明显的阶段性特征和较大的差异[18]。郑循刚认为我国农业生产技术效率存在显著的区域性差异，且东部地区高于中西部地区[19]。曹跃群等认为在1997—2005年我国东部地区的农业技术效率显著高于中西部地区[20]；田伟等认为我国农业生产的技术效率存在明显的地区差异且差距在不断扩大，同时呈现出不同的收敛特征[21]。

通过对现有文献的梳理发现，我国农业生产技术效率研究内容不断细化，研究方法不断改进，但在取得了一定成效的同时也存在一些争议：一是因为学者们选取的研究时间段不一样，得出的技术进步和技术效率对农业增长的贡献方向虽大体一致，但贡献大小差异较大；二是在对区域性差异的分析上，部分学者认为技术进步和技术效率均按东中西次序依次高低排列，这与本研究相悖，这可能与选取的样本省份有关。在尽可能扩展研究时间段范围和详尽讨论区域性差异的基础上，本研究还探讨了受灾面积和有效灌溉面积对技术效率变化的影响。

2 随机前沿生产函数模型的构建与设定

本研究采用Battese和Coelli随机前沿生产函数模型，基本函数形式设定如下：

Yit=F(Xit，t) exp(vit-uit)；

uit={exp[-η(t-T)]}ui。

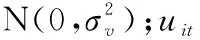
根据Battese和Coelli的设定，技术效率损失函数表示为mit=zitδ，其中，zit表示影响生产决策单元技术效率的p维向量，δ为须要估计的参数向量。

本研究生产函数的设定，采用非中性技术进步的扩展型C-D生产函数，因为在多数文献中资本与劳动的替代弹性接近于1，具有常替代弹性性质，同时因为样本容量的限制不适合采用超越对数生产函数，否则会由于要素交互项的引入而引起多重共线性问题。生产函数设定如下：

将技术效率定义为

TEit=exp(-uit)。

式中：uit表示非负的技术无效率项。当uit=0时，TEit值为1，不存在效率损失(生产单元处于生产前沿面上)；当uit趋于无穷大时，TEit值为0，则存在完全的技术效率损失。

技术效率损失函数定义为

mit=δ0+δ1are+δ2irr。

式中：δ0表示常数项；δ1表示由受灾率变化引起的技术效率损失的变化情况；δ2表示由有效灌溉面积率变化引起技术效率损失的变化情况；are表示受灾率，即受灾面积占其总播种面积的比例；irr表示有效灌溉面积率，即有效灌溉面积占其播种面积的比重。

3 实证分析

3.1 变量及数据说明

本研究选取1990—2012年全国13个农业大省的农业投入和产出数据(因2013年起所选样本省份对农业劳动力的统计指标，部分为“农林牧渔劳动力总人口”，部分为“第一产业劳动力总人口”，为保证统计口径一致，数据选取至2012年)，所有数据均来自于《中国统计年鉴》。各变量定义见表1。

各主要变量的描述性统计结果见表2。

3.2 随机前沿生产函数及无效率方程估计

3.2.1 随机前沿生产函数估计结果 本研究使用Frontier 4.1软件，采用3步法对随机前沿生产函数进行回归，回归结果见表3。

从回归结果来看，首先对数似然值和对数似然比通过检验；γ值为0.999 0，说明生产的无效率主要是由技术无效率引起的，而来自于统计误差、天气、自然灾害等随机因素的外部影响作用只有0.1%，说明该模型具有较强的解释力。

其次，Labor、Land、Fer、Mac都通过了显著性检验，表明这些要素投入对农业生产均产生了显著的影响。其中，Labor通过0.1显著性检验，影响显著为负，这主要是由于农村存在剩余劳动力造成的；Mac通过0.01显著性检验，影响为负，表明农村在使用机械化操作时可能存在效率较低的粗放的投入，进而资源被浪费；Land通过0.05显著性检验，Fer通过0.01的显著性检验，均对农业生产产生了正向作用，这与传统研究和实际认识相一致。

表1 变量定义及说明

表2 主要变量的描述性统计分析

表3 随机前沿生产函数估计结果

注：*、**、***分别表示在0.1、0.05、0.01水平上显著。表4同。

最后，t通过0.01显著性检验，说明13个省份的农业生产均存在技术进步。Fer与t的交叉项的系数、Land与t的交叉项的系数均通过了0.01显著性检验，说明技术进步是非中性的；Labor和t交叉项的系数、Mac和t交叉项的系数均不显著，表明在研究期内劳动投入、农业机械投入的变化并没有随技术进步表现出明显的变化趋势。Fer与t的交叉项的系数显著为正，表明在研究期内随着技术不断进步，化肥投入的贡献率在增加，化肥的施用对农业生产依然有着正向的推动作用；Land与t交叉项的系数显著为负，表明在研究期内随着技术不断进步，播种面积投入的贡献率在减少，这表明随着技术进步依靠扩大播种面积来促进农业生产的方式并不能长时间为继。

3.2.2 生产无效率方程估计 由表4可知，受灾面积比例are对农业生产技术无效率有显著的正向影响，即随着受灾程度增加，效率损失会增加，技术效率会降低，这与我国的农业生产实际情况相符，目前我国农业发展仍然较易受气候、自然灾害的影响，应当引导农民积极做好防范和预警措施。有效灌溉面积比例irr对农业生产技术无效率具有显著的负效应，即随着有效灌溉面积的增加，效率损失减少，技术效率增加，所以应当加强灌溉基础设施建设、做好农业水资源调控。

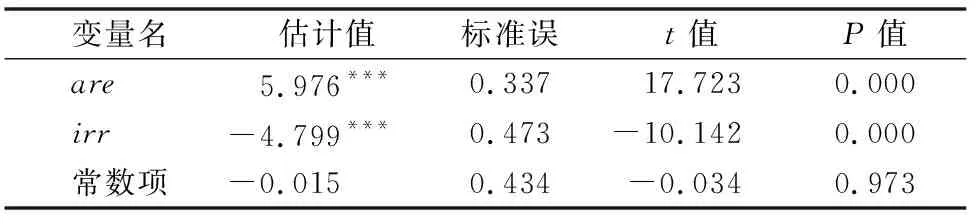
表4 生产无效率方程估计结果

3.3 技术效率分析

技术效率表示生产决策单元的实际产出和最大潜在产出之间的差距，反映的是决策单元对现有资源的利用能力。样本省份各年技术效率值如表5所示。

所有样本省份1990—2012年的平均技术效率见图1，总体来看，呈现上下无规律波动趋势，没有明显的单调上升或下降趋势。但是最高的也只是1995年的0.79，都没有超过 0.80，距离1.00还是有一定的差距，最低的为1993年的0.58，整体范围在0.60～0.70之间波动。

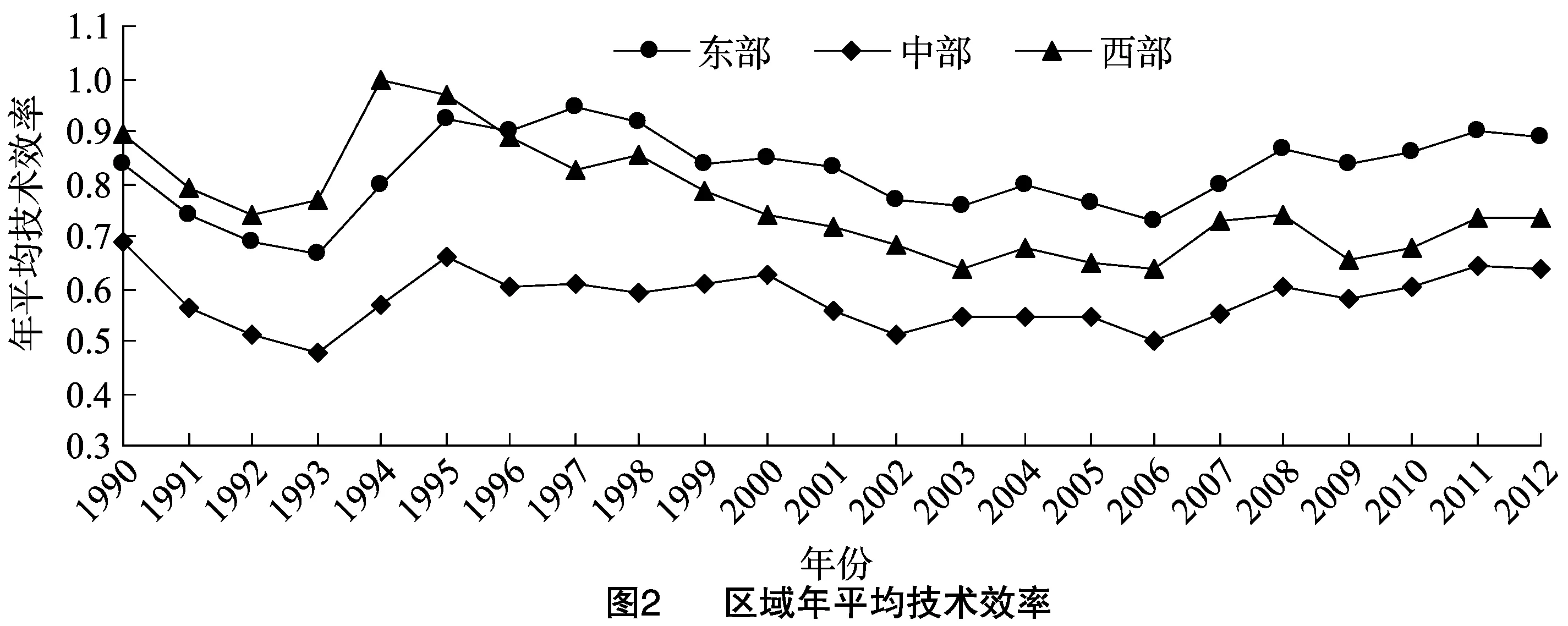
为了分析技术效率的区域性差异，将13个样本省份按地理位置分为东、中、西部3个区域，3个区域的平均技术效率变化见图2。东部和西部的平均技术效率要远高于中部，说明对现有资源的利用能力，东部和西部远高于中部。可能的原因：劳动力方面，东部具有先进的生产技术条件，再加上具有非农就业的良好优势和条件，所以技术效率较高；西部地区虽然生产条件不先进，地形地貌等也不利于现代化农业生产，但不代表对现有资源利用率低，这可能是因为西部地区剩余劳动力大规模流向东部沿海等地区，并且在现有的不先进的生产条件下能尽可能地利用现有资源和条件；中部地区可能因为经济条件较为发达，程度介于东部和西部之间，其没有东部良好的非农就业条件， 也没有像西部一样大规模转移剩余劳动力，但有其自身特征，比如兼业化和就地转移，如果将这部分劳动力算作农业劳动力，势必会降低农业产出效率，但如果将其剥离出农业劳动力，又忽略了其作为农业生产投入的作用。机械投入方面，东部地区不仅采用先进的机械设备，同时具有发达的外包服务市场，所以技术效率较高，西部地区虽然不具有先进的农机设备和发达的外包市场，但是其能在现有机械装备条件下尽可能地利用现有设备；中部地区虽然具有比西部地区先进的农机设备，但是可能因为土地流转制度落后和外包服务市场滞后等，没能让现有机械设备发挥较高的利用效率。

表5 样本省份各年技术效率值

3.4 技术进步率变化分析

从图3中可以看出，3个区域的技术进步率从高到低依次是东部、中部、西部；同时，3个地区的技术进步率整体都呈上升趋势，东部、西部呈稳定上升趋势，中部上下波动明显。根据速水-拉坦的诱致性技术变迁理论可知，农业生产非优势地区多数经济发达，产品市场和要素市场都比较发达，要素价格也相对较高，这就使得该地区会率先寻求和使用新技术，比如机械、生物化学技术等替代价格更高的土地和劳动力，进而技术进步率加快。

4 结论与建议

本研究利用1990—2012年我国13个农业大省的投入产出数据，通过构建随机前沿生产函数模型，对我国农业生产效率及其区域性差异进行测定和分析，得出以下结论。

我国农业增长呈现农业技术进步较快与农业技术效率不高并存的特征。生产前沿面的不断上移说明我国的农业生产存在明显的技术进步，较低的技术效率水平说明我国农业生产对现有资源的利用能力较低，技术推广和技术扩散作用不明显，须要继续加大技术推广力度。

我国的农业增长方式存在明显的区域差异。经济发达的地区，如东部，农业技术进步率较高、增速较快，技术效率水平也较高但增速较慢且波动明显，表明该地区的农业增长进程为技术和效率双重驱动特征；经济较发达地区，如中部，技术进步率偏高，技术效率偏低，甚至低于西部，说明中部地区农业增长的驱动力主要是技术进步，同时其对现有资源的利用能力有很大的提升空间；经济欠发达地区，如西部，技术进步率偏低、技术效率偏高，说明该地区对现有资源的利用能力较高，但经济不发达是其技术进步受阻的主要原因。

因此，未来我国农业增长在促进技术进步的同时，更须重视对现有资源利用能力的提升及技术效率的提升，进而实现技术和效率双重驱动型的增长方式。分区域来看，东部地区须要同时保持并提高技术进步率和技术效率，进而持续为技术和效率双重推进模式；中部地区须要优先提升技术效率、提高现有资源的利用能力，诸如提高要素的投入产出效率、加大农业科技成果的示范推广及应用等，次之考虑技术进步；西部地区当下须要解决的问题是提高技术进步，即加大该地区农业科研资金的投入和政策制定，注重新品种研发、技术创新和研发制度的创新。