水下多目标跟踪技术现状与展望
2019-01-09张思宇何心怡
张思宇, 何心怡, 张 驰, 祝 琳, 陈 双
水下多目标跟踪技术现状与展望
张思宇, 何心怡, 张 驰, 祝 琳, 陈 双
(海军研究院, 北京, 100161)
水下多目标跟踪技术在军事和民用方面均有重要作用, 是军民融合发展中的重点技术。针对水下水文条件复杂、作用距离相对较小等不利因素, 文中根据跟踪滤波算法原理的不同, 分别论述了基于数据关联的水下多目标跟踪技术和基于随机有限集的水下多目标跟踪技术, 详细阐述了其目标运动模型、跟踪滤波方法和应用现状, 梳理了在水下实现多目标跟踪关键的数据关联技术和随机有限集技术的性能, 分析了由于漏报和虚警导致观测信息的不确定、跟踪过程中目标数量不确定和运动状态以及跟踪算法实时性差等3类技术瓶颈, 突显了建立统一的随机有限集框架描述跟踪问题解决该类瓶颈的优势。在此基础上, 根据作战使用和海洋开发的要求, 展望了水下多目标跟踪技术发展方向, 供相关研究人员参考。
水下多目标跟踪; 数据关联; 随机有限集
0 引言
水下目标跟踪技术在海洋资源勘探、水下工程作业、海战场监视及水中兵器精确自导等方面用途广泛, 有着广阔的军民融合发展前景。该技术通过对量测的目标数量和状态信息实时处理, 维持对目标数量和运动状态准确估计的过程。根据探测器的数量和被跟踪目标数量的不同可分单个探测器跟踪单个目标(one-to-one, OTO)、单个探测器跟踪多个目标(one-to-multiple, OTM)、多个探测器跟踪单个目标(multiple-to-one, MTO)及多个探测器跟踪多个目标(multiple-to-multiple, MTM)等4类情形, 其中OTM、MTO、MTM等3类情形要通过多个探测器之间的数据传输、数据融合和对多个目标的量测信息进行数据关联, 技术实现较为复杂。与雷达系统目标跟踪应用场景相比, 声呐系统由于应用场景的水文条件复杂、作用距离相对较小、量测信息误差大, 同时又存在和电磁波相比声速很慢、系统数据刷新率低、能观性差以及滤波收敛慢等问题, 使得跟踪实现难度更大。
经过50多年的研究发展, 多目标跟踪理论在实际工程应用中取得重大突破, 部分最新服役的鱼雷等精确制导水中兵器具有多目标跟踪能力[1]。如美国的MK54鱼雷、法意联合研制的MU90鱼雷及意大利研制的“黑鲨”鱼雷等均具备定位且同时对多个目标进行跟踪的能力, 可自动判断最具威胁的目标并辨识出真假目标。
多目标跟踪问题最早由Wax[1]于1955年提出, 到上世纪70年代, 随着计算机技术的发展, 逐步受到学者的广泛重视和研究。Singer等[2]提出了最近邻算法, 以目标统计距离最小值作为目标跟踪门限, 实现多目标跟踪, 但仅适用于高信噪比的跟踪背景。Fortmann等[3]于1983年提出了联合概率数据关联算法, 通过计算每个量测信息和所有可能目标的相关概率, 筛选出最佳关联概率, 进行多目标跟踪, 但存在计算量巨大的缺陷。Reid[4]基于Singer和Fortmann等的贡献提出了多假设跟踪算法, 通过时延逻辑, 实现有效的多目标航迹保持, 该算法计算量小, 但存在对多目标的先验信息依赖程度高的缺陷。2003年, Mahler[5]首次提出了基于随机有限集的多目标跟踪算法, 受到学界的广泛关注。Vo等[6]对相关算法进行改进, 使基于随机有限集的多目标跟踪算法取得了长足的进步。
文中系统梳理了水下多目标跟踪技术相关文献, 总结评述了传统基于数据关联的多目标跟踪技术和新兴的基于随机有限集的多目标跟踪技术的目标运动模型、跟踪算法、应用现状及当前的技术瓶颈, 并展望了技术发展方向, 以期为相关研究提供参考。
1 基于数据关联的多目标跟踪
该跟踪方法除了涵盖单目标跟踪理论的建立目标运动模型、选取合适的跟踪坐标系、跟踪滤波与状态预测等关键环节外, 还产生了跟踪门、数据关联与维持、跟踪的起始与终结、虚警与漏报等主要处理步骤, 其核心是确定探测器接收到量测信息和目标源对应关系的数据关联[7]。多目标跟踪利用贝叶斯方法将多目标跟踪问题转化为单目标跟踪问题, 进而递推处理, 其基本原理如图1所示。
首先, 利用目标的数量和状态的量测信息更新已有轨迹, 通过设定的跟踪门判定量测信息和已有轨迹的配对情况, 进而用数据关联确定量测数据与已有轨迹的最佳配对, 通过机动辨识和跟踪滤波保证整个跟踪过程的维持。来自新目标或杂波的量测信息和已有轨迹是互不相关的, 通过跟踪起始的方法进行判别新目标的真假, 对真目标建立新的轨迹档案。当目标离开跟踪区域, 通常及时结束跟踪, 并删除目标轨迹档案, 避免无效计算。在整个过程中, 跟踪门的大小和中心位置要根据目标状态估计实时调整, 确保跟踪精度。以下对多目标跟踪的关键环节进行逐一概述。
1.1 目标运动模型的建立
建立合适的目标运动模型要从两方面考虑, 一是模型要准确地描述目标的运动状态, 即尽可能涵盖运动的全面特性, 如目标位置、速度、加速度和描述外界引起的不可预知现象的状态噪声等; 二是建立的模型数学处理简单, 要求状态向量的维数尽可能少, 对一些变量进行近似和简化, 保证计算效率和跟踪的实时性。因此, 如何建立合理的模型经历了由简单模糊到复杂精准的过程, 主要有匀速运动(constant velocity, CV)和匀加速运动(constant aceleration, CA)模型[8]、辛格(singer)模型[9]、半马尔科夫过程模型[10-11]、目标运动“当前”统计模型和交互式多模型(interacting multiple model, IMM)[12]等描述目标运动的模型。
1) CV和CA模型
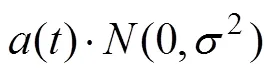


2) Singer模型
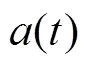
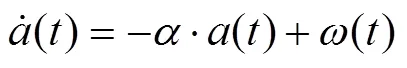

Singer模型采取有色的噪声分布描述机动加速度, 更贴近目标的实际运动状态, 故跟踪效果较好, 应用广泛; 但是潜艇等水下目标发现受到攻击, 一般会采取大机动规避动作。此时, Singer模型与实际偏差较大, 很难准确跟踪目标, 甚至会失跟。
3) 半马尔科夫模型
为了克服Singer模型在做目标大机动规避时, 估计误差较大的局限, Moose[11]提出了应用半马尔可夫过程描述目标机动过程。
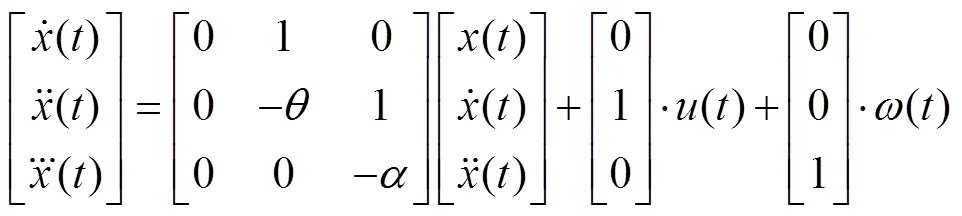
4) 目标运动“当前”统计模型
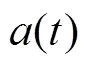
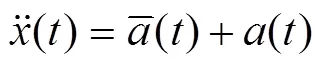
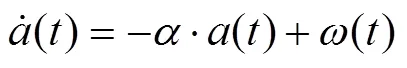

由于该模型的“当前”加速度是基于机动加速度统计量均值的预测值, 且服从修正瑞利分布的时间相关模型, 故对目标运动状态描述更符合实际。
5) IMM模型
由于机动目标的运动状态的不确定性, 单一目标运动模型难以准确描述目标实际运动, 故Blom等[12]提出用不同的机动目标运动模型来描述不同的运动状态, 以马尔可夫过程来描述不同机动模型之间的转移概率, 用卡尔曼滤波实现机动模型和目标运动状态估计。从模型理论上讲, 如果构建所有运动模型则可实现对机动目标状态的最佳估计。但是, 目标机动存在不确定性, 工程实践中通常运用以上几个典型的机动目标模型近似描述机动目标实际运动状态。该模型不需要对机动目标进行检测, 可以实现全面自适应选择, 是一种能够较好描述大机动目标的机动目标模型, 故可被广泛应用[14]。
1.2 跟踪滤波与状态预测的确定

1.2.1 线性滤波

机动目标的运动过程一般可以用稳态过程和暂态过程来描述, 而上述滤波算法都有其对应的合适的运动过程, 需要依据实际情况选择。另外, 根据滤波算法的实现精度和目标轨迹的实时性来鉴定系统整体性能, 从跟踪精度来评价, 精度最高的是卡尔曼滤波, 但是计算时间最长; 从跟踪实时性来评价, 两点外推算法计算时间最短, 实时性强, 但是精度较低。随着现代微型计算机性能大幅提升, 系统能够满足卡尔曼滤波的运算要求, 在线性高斯白噪声模型中, 卡尔曼滤波是最佳选择。
1.2.2 非线性滤波
非线性运动模型更符合目标的实际运动, 故非线性滤波方法有较高的精度。根据估计方法不同, 可将非线性滤波分为点估计和概率密度估计两大类。其中, 点估计根据逼近方法不同可分为: 函数逼近类, 如扩展卡尔曼滤波; 统计逼近类, 如无迹滤波; 随机模型逼近类, 如中心差分滤波。而概率密度估计应用最多的是粒子滤波。文中主要评述以下3种最常见的非线性滤波方法。
1) 扩展卡尔曼滤波(extended Kalman filter, EKF)算法是卡尔曼滤波在处理非线性跟踪滤波问题的扩展, 一般用Taylor级数展开法对非线性的目标运动状态方程或量测状态方程线性近似[14]。该算法的优点在于Taylor级数展开将非线性问题线性近似, 算法较简单, 能以较小的计算量取得较好的跟踪滤波效果, 工程实现性好, 应用广泛。其局限是由于该算法只是一种有限的线性化近似, 处理非线性度较高的系统时, 其模型的线性化误差较大, 滤波精度低, 甚至可能出现滤波发散。
2) 无迹卡尔曼滤波(unscented Kalman filter, UKF)算法是利用机动目标模型初始分布的均值和协方差确定一系列sigma采样点, 将采样点通过非线性转移, 进而估计出目标的均值和协方差[18]。该算法直接求出目标的均值和协方差, 不会产生非线性系统线性化的近似误差, 故跟踪精度要高于EKF。但是, 处理4维以上系统会出现非正定协方差, 导致滤波信息输出不稳定, 甚至发生滤波发散, 所以难以应用到高维系统处理。
3) 粒子滤波(particle filter, PF)算法是利用序贯蒙特卡洛(sequential Monte Carlo, SMC)方法直接逼近非线性系统概率密度函数, 再加权求和估计出目标运动状态的一种滤波算法[22]。该算法的优点是不受机动目标模型限制, 能够处理在非线性非高斯动态过程中的机动目标跟踪问题, 可减少计算量, 在未知目标数量的条件下, 实现有效估计。但该算法的粒子退化问题是序贯重要性采样难以消除的, 在多次迭代计算后, 除少数粒子权值有效外, 绝大多数粒子权值趋零, 造成大量无效加权求和。且跟踪精度和滤波收敛性只能依靠大量粒子, 计算量大, 难以保证跟踪实时性。
综合以上各种滤波算法的实质就是求取最大后验概率的最优估计问题。卡尔曼滤波是线性高斯白噪声条件下的最优滤波器, EKF是非线性非高斯有色噪声条件下的次优滤波器, 以上在未知目标数量的条件下, 滤波性能较差。基于SMC方法的PF能有效破解上述难点, 但目前计算量大和粒子衰退问题是需攻克的难点。从工程实际出发, 采用基于点估计的滤波算法, 可以以较高的精度估计目标状态, 计算量小, 跟踪实时性好, 系统成本较低。
1.3 多目标跟踪的基本要素
1.3.1 跟踪门的形成
跟踪门作为跟踪空间的一个子空间, 其大小取决于接收正确量测信息的概率大小, 以目标估计的运动状态作为中心。跟踪门是将观测信息与已有目标轨迹或新建目标轨迹配对的一种预先粗检手段, 如果探测器接收到的量测信息符合已设定的跟踪门, 则将该量测信息作为已有目标的回波, 估计并更新目标状态; 如果量测信息没有落在跟踪门内, 则将该信息视为虚警或者有新目标进入, 再进一步判断采取摒弃该信息还是建立新的候选目标轨迹。
1.3.2 跟踪起始与跟踪终结
跟踪起始是通过形成假设目标轨迹、初始化目标轨迹和确定目标轨迹等3个步骤, 对新进入监视区域的目标, 建立轨迹档案的决策方法。跟踪起始在量测信息与已有目标轨迹不能配对时发起, 通常采用次扫描中出现次相关的方法降低虚警概率, 保证跟踪起始的有效性。
跟踪终结是发现目标离开监视区域后, 删除其轨迹档案的决策方法, 可增加有效存储, 提高计算速度, 增强跟踪的实时性。
1.4 数据关联算法
数据关联是处理目标不确定性和量测不确定性的关键方法, 也是该跟踪方法的最核心环节[23]。一般从面向目标、面向量测及面向航迹这3个方向设计数据关联算法, 分别是基于观测值是来自已知目标还是杂波、量测信息是来自已知目标还是新目标或杂波和目标轨迹是跟踪起始、跟踪维持还是跟踪终结等3类情况考虑的。
1)“最近邻”数据关联算法
该算法是根据目标状态估计值设计跟踪门初步筛选所接收的量测信息作为初步候选回波, 进一步筛选出和目标状态估计值的统计距离最小的量测信息作为候选回波, 然后将候选回波应用上述的单目标跟踪滤波算法估计出目标运动状态。该算法优点是能在高信噪比和目标稀疏的条件下, 以较小的运算量实现较高精度的跟踪, 工程实现较简单; 但是由于舰艇编队密集或水文环境不佳时, 密集的量测信息回落于同一跟踪门内, 则统计距离最小的候选回波不一定是目标回波, 容易出现虚警, 易产生误跟或失跟的现象。
2) 联合概率数据关联(joint probability data association, JPDA)算法
由于利用概率进行关联的算法只能用于多目标跟踪门不重叠或者没有多个目标回波落在同一跟踪门的条件下, 通过对所有可能的量测信息加权平均估计出目标运动状态的局限, 推广出了JPDA算法。该算法通过计算每个量测信息和所有可能目标的相关概率, 筛选出最佳关联概率, 进一步估计出目标运动状态。该算法历遍所有量测信息和所有可能目标, 在密集多目标和多杂波的情况下, 有较好的跟踪效果; 但也存在目标数量较多时, 计算量太大导致组合爆炸的问题。
3) 轨迹分裂数据关联算法
轨迹分裂数据关联算法的基本原理是在接收到多余目标回波时, 按照现有新的目标轨迹数分裂原有轨迹与之对应, 进而求出每一条轨迹的似然函数, 仅保留高于门限的回波, 舍弃低于门限的回波。其优点是可以有效发现并舍弃虚警轨迹; 但是在密集多目标和多杂波情况下, 系统计算和存储压力很大, 有组合爆炸的可能。
在现有计算能力下, 由于目标不确定性和量测不确定性的限制, 数据关联算法存在计算量小则跟踪精度低, 跟踪精度高则计算量大的矛盾。故可将模糊推理、模糊聚类、模糊数学结合神经网络和目标属性与状态识别等新技术应用于数据关联算法, 以期解决复杂水下环境背景的密集多目标跟踪难题。
2 基于随机有限集的多目标跟踪
传统基于数据关联的多目标跟踪算法, 实质仍是通过数据关联将多目标跟踪转换化为单目标跟踪, 难以实现多源多目标数据融合和突破计算量大的瓶颈。Mahler[24]于2007年首次提出了基于随机有限集(random finite set, RFS)的多目标跟踪算法, 将每一个目标状态和量测信息视为随机有限集结, 进而通过贝叶斯滤波算法直接估计出目标数量和运动状态, 给出了相关近似算法, 有力地推动了该技术的发展。该算法能够将5级的信息融合均统一于RFS的框架下, 较好实现数据关联困难的复杂环境下密集多目标跟踪问题, 受到业界的广泛关注[15-28]。目前, 美国在该方法的研究取得了很大的理论进展和应用成果, 如洛马公司的反潜多目标跟踪识别系统[5, 24]、海军研究办公室的被动声呐反潜信息融合和目标识别系统[6, 26]。国内也有许多研究机构开展了大量的探索工作, 取得了一些初步的研究成果, 但离实际应用仍有差距[29-36]。
该算法也是利用贝叶斯滤波递推计算, 区别在于其是对随机有限集进行积分, 如式(9)和式(10)所示[17]。

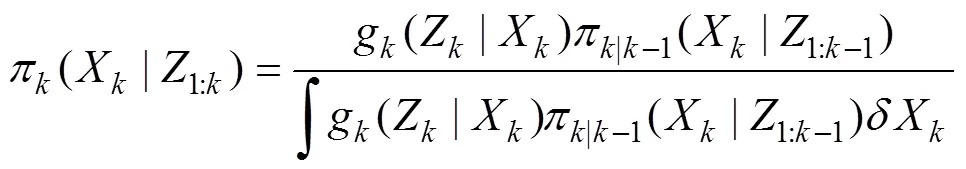
由上式可见, 对随机有限集积分很难求解, 故Mahler等提出了许多近似的多目标滤波算法, 如: 概率假设密度(probability hypothesis density, PHD)滤波算法[26]、势概率假设密度(cardinalized probability hypothesis density, CPHD)滤波算法[30]和多伯努利(multi-Bernoulli, MB)滤波算法[27]等。
2.1 基于RFS的跟踪系统模型


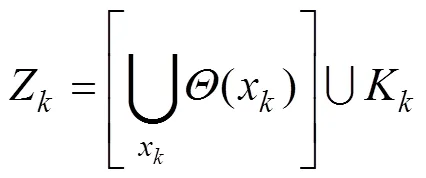
一般情况下, 各集合之间相互独立, 其模型如图2所示。
2.2 基于RFS的跟踪滤波算法
Mahler[24, 26-27, 30]首先给出了单传感器探测多目标背景下的最优贝叶斯滤波器-多目标联合跟踪滤波器(joint target-detection and tracking, JoTT), 并针对目标数未知、最优贝叶斯滤波器无法实现的问题, 进一步推导出概率假设密度滤波器、势概率假设密度滤波及多目标多伯努利滤波器。Vo[31]针对多目标多伯努利滤波器的目标数有偏估计问题, 推导了势平衡多目标多伯努利滤波器, 提高了估计目标数的能力。
1) PHD滤波算法。该算法是将多目标状态空间利用假设的后验概率密度转换到单目标状态空间, 避免了计算复杂的数据关联过程[15]。其核心是通过多目标状态概率假设密度函数的1阶矩求得后验概率密度, 进而估计多目标状态。对于任一监视区域, 其集值积分为
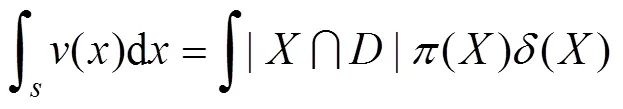
2) CPHD滤波算法。鉴于PHD算法的不足, Malher[39]提出了以递推的形式同时传播目标状态概率假设密度函数和目标数的后验概率分布, 且只需利用目标数分布函数即可估计出目标个数的算法, 即CPHD跟踪滤波算法。该算法也是通过GM和SMC[41-42]方法来实现线性和非线性条件下多目标跟踪, 并在具体问题有对应的改进算法, 如可通过EKF的思想, 将非线性函数近似线性化, 利用GM-CPHD滤波器在线性系统下处理; 也可运用粒子滤波的思想, 对SMC-CPHD滤波器进行优化, 提高滤波性能。总的来说, 运用CPHD滤波算法可以提高滤波和跟踪的精度, 但随着计算复杂程度和计算量的增加, 增大了工程的实现难度。
3) MB滤波算法[43-46]是通过传播一个多伯努利随机有限集参数来近似多目标后验概率密度, 进而估计目标个数和状态信息。但是Beard[43]和Schuhmacher[45]指出, MB滤波算法是一种有偏估计, 因而改进为势平衡多伯努利滤波(cardinality balanced multi-target multi-Bernoulli, CBMeMBer)算法, 并提出了线性条件下GM实现和非线性非高斯条件下SMC实现方法。由于CBMeMBer算法提出时间不长, 仍有许多问题有待解决, 是当前的研究热点之一。
综上, 基于随机有限集的多目标跟踪滤波器, 根据目前公开发表的文献来看, GM-CPHD在线性高斯条件下性能最好, 是最优贝叶斯滤波器; 在非线性非高斯程度很高的环境中, CBMeMBer滤波器能够改进目标数的有偏估计, 且计算量较小, 跟踪精度高和并可直接获取目标状态。故建议根据具体问题, 如在线性高斯条件下, 选择基于GM-CPHD改进的滤波器; 在非线性非高斯条件下, 选择基于SMC-CBMeMBer的次优贝叶斯滤波器。在水下多目标跟踪实现上, Peter团队[40]已有初步应用, 采用GM-PHD滤波器取得了较好的多传感器的多目标跟踪效果; 刘姝琴等[14]初步探索了如何利用水下无线传感器网络(underwater wireless sensor network, UWSN)实现多目标跟踪。
2.3 基于RFS的跟踪滤波性能评价指标
该跟踪滤波方法没有采用数据关联过程, 故传统将多目标跟踪转化为多个单目标跟踪的评价方法不再适用。基于此, 有学者提出以合理量测2个随机有限集之间的距离作为新的评价指标。主要有Hausdorff距离[45]、Wasserstein距离[46]和OPSA(optimal subpattern assignment)距离[47]等3种评价指标。
Schuhmacher等[45]提出了Hausdorff距离是度量RFS的性能的最初标准, 能够表现出目标状态和数目估计的局部性能。但是, 该度量方法没有定义出现空集时Hausdorff距离的意义, 且对RFS之间的势差异不敏感, 无法给出跟踪性能的准确评价。Nagappa等[46]提出了Wasserstein距离是统计学中度量非空集合之间距离的方法, 其比Hausdorff距离对RFS的势差更敏感, 当2个RFS的势大小相同时, 是最优关联下的距离; 但是也存在出现空集时, 距离无意义, 且对RFS的势差敏感, 目标数量估计可能出现错误惩罚。Ristic等[47]提出了OPSA距离是对Wasserstein距离的一种改进度量方法, 其优点是在出现空集情况, OPSA距离都具有一定物理意义。Ristic等[47]和He等[48]在RFS的势误差和状态估计误差的基础上, 并入估计质量信息, 提出了更高估计精度的Q-OPSA距离, 提高了度量多目标跟踪精度。
综述以上的度量方法, 由于目标估计质量信息一般很难保证, 故目前OPSA距离是认可度较高的基于随机有限集多目标滤波评价指标。
3 水下目标跟踪技术展望
攻防装备发展是一个此消彼长、螺旋上升的发展过程, 随着装备的隐蔽性和机动性能的提高, 海区监视、鱼雷打击目标和反鱼雷作战的难度也不断增大, 从当前和未来一个时期作战使用需求来看, 水下跟踪技术应重点朝以下几个方向发展。
1) 随着敌方舰艇战场感知能力增强和海战场大范围监控的任务需要, 对隐蔽、大范围跟踪监视系统的需求也日益加强。因此, 应大力发展多基地声呐监视系统, 发挥其跟踪监视范围大、可靠性高和己方舰艇隐蔽性强的优势, 提高我国重点海区的水下跟踪监视能力, 保证国家海洋安全。
2) 鉴于鱼雷攻击距离的增大, 对自身隐蔽性要求的提高, 以及打击舰艇编队和具备水声对抗能力的单艇目标, 需要具备真假目标识别和多目标跟踪的能力。因此, 因重点提高鱼雷自导系统的测量精度, 克服水下可观测性差, 跟踪收敛慢的困难。同时, 应在自导系统引入目标识别功能, 有效提高鱼雷发现并攻击真目标和高价值目标的能力。
3) 随着海洋开发的日益深入和海军走向远海大洋, 存在着许多不适合布放声呐阵列的海域海况环境。因而, 应重点关注和发展UWSN, 发挥其布放简单、成本低廉、容错和抗毁伤能力强的特点, 拓展水下跟踪监视的范围。
4) 随着多源多目标跟踪技术的不断发展, 传统基于数据关联的滤波算法难以适应信息融合的需要。因此, 要重点研究基于RFS的跟踪滤波算法, 突破计算复杂度高和多目标状态提取困难的限制, 追赶国际先进水平, 加快其工程应用进度。
5) 高实时性多功能目标跟踪系统。随着各方面技术的发展和作战需求牵引, 水下目标跟踪系统呈现向集成目标探测识别、预警跟踪和水下通信等综合系统的方向发展。应加强DSP和现场可编程门阵列(field-programmable gate array, FPGA)等专用高速处理器的使用, 进行相应的高速计算语言和算法的关注, 以突破水下目标跟踪数据量巨大, 跟踪实时性差的瓶颈。
4 结束语
现代海战是体系与体系的对抗, 准确感知战场环境, 精准毁伤目标是决定战争胜败的关键因素之一, 而水下目标跟踪技术是其关键环节。文中根据跟踪滤波算法原理的不同, 分别论述了基于数据关联的水下多目标跟踪技术和基于随机有限集的水下多目标跟踪技术, 详细阐述了其目标运动模型、跟踪滤波方法和应用现状及其技术性能, 分析了存在的技术瓶颈。并根据作战使用和海洋开发的要求, 展望了水下多目标跟踪技术发展方向。同时可以看出, 基于随机有限集的多目标跟踪技术能够较有效克服传统多目标跟踪算法的3类瓶颈问题, 仍处在理论向工程实践转化的关键阶段, 应为技术人员着力重点突破的方向。
[1] Wax N.Signal-to-noise Improvement and the Statistics of Track Populations[J].Journal of Applied Physics, 1955, 26(5): 586-595.
[2] Singer R, Stein, J.An Optimal Tracking Filter for Proces- sing Sensor Data of Imprecisely Determined Origin in Surveillance Systems[C]//IEEE Conference on Decision and Control, Miami Beach: IEEE, 1971: 171-175.
[3] Fortmann T E, Bar-Shalom Y, Scheffe M.Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J].IEEE Journal of Oceanic Engineering, 1983, 8(3): 173-184.
[4] Reid D B.An Algorithm for Tracking Multiple Targets [J].IEEE Transactions on Automatic Control, 1979, 24(6): 843-854.
[5] Mahler R.Multi-target Bayes Filtering Via First-order Multi-target Moments[J].IEEE Transactions on Aerosp- ace and Electronic Systems, 2003, 39(4): 1152-1178.
[6] Vo B-N, Singh S, Doucet A.Sequential Monte Carlo Methods for Multi-target Filtering with Random Finite sets[J].IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.
[7] 刘妹琴, 兰剑.目标跟踪前沿理论与应用[M].北京: 科学出版社, 2015.
[8] 周宏仁, 敬忠良, 王培德.机动目标跟踪[M].北京: 国防工业出版社, 1991.
[9] Singer R A.Estimating Optimal Tracking Filter Performance for Manned Maneuvering Target[J].IEEE Transactions on Aerospace and Electronic Systems, 1970, 6(4): 473-483.
[10] 党建武.水下多目标跟踪理论[M].西安: 西北工业大学出版社, 2009.
[11] Moose R L.An adaptive state estimation solution to the maneuvering target problem .IEEE Transactions on Automatic Control, 1975, 20(6): 359-362.
[12] Blom H A P, Bar-Shalom Y.The IMM Algorithm for Syst- em with Markovian Switching Coefficients[J].IEEE Tr- ansactions on Automatic Control, 1988, 33(8): 780-783.
[13] 周宏仁.机动目标当前统计模型与自适应跟踪算法[J].航空学报, 1983, 4(1): 73-86.Zhou Hong-ren.Current Statistical Model and Adaptive Tracking Algorithm for Maneuvering Targets[J].Acta Aeronautica et Astronautica Sinica, 1983, 4(1): 73-86.
[14] Song T L.Observability of Target Tracking with Bearing- only Measurements[J].IEEE Transactions On Aerospace & Electronis Systems, 1996, 32(4): 1468-1471.
[15] 严卫生, 高磊, 张礴, 等.水下目标跟踪技术[J].火力与指挥控制, 2000, 25(2): 2-6.Yan Wei-sheng, Gao Lei, Zhang Bo, et al.Underwater Target Tracking Technology[J].Fire Control & Command Control, 2000, 25(2): 2-6.
[16] Bar-Shalom Y, Tse E.Tracking in a Cluttered Environment with Probabilistic Data Association[J].Automatica , 1975, 11(5): 451-460.
[17] Ristic B, Arulampalam S, Gordon N.Beyond the Kalman Filter: Particle Filters for Tracking Application[M].Bos ton London: Artech House, 2004.
[18] 高剑, 徐德民, 严卫生, 等.无迹卡尔曼滤波及其在三维水下目标跟踪系统中的应用[J].船舶工程, 2005, 27 (3): 24-28.Gao Jian, Xu De-min, Yan Wei-sheng, et al.Unscented Kalman Filter and Its Application in 3D Underwater Target Tracking System[J].Marine Engineering, 2005, 27(3): 24- 28.
[19] 吴盘龙, 孔建寿.基于平方根UKF的水下纯方位目标跟踪[J].南京理大学学报(自然科学版), 2009, 33(6): 751-755.Wu Pan-long, Kong Jian-shou.Underwater Pure Azimuth Target Tracking Based on Square Toot UKF[J].Journal of Nanjing Institute of Science Natural Sciences, 2009, 33(6): 751-755.
[20] Popp R L, Pattipati K R, Bar-Shalom Y.M-Best S-D Assignment Algorithm with Application to Multitarget Trac- king[J].IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(1): 22-39.
[21] Bar-Shalom Y.Update without of Sequence Measureme- nts in Tracking: Exact Solution[J].IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(3): 769-778.
[22] Li T, Bolic M, Djuric P D.Resampling Methods for Particle Filtering[J].IEEE Signal Processing Magazine, 2015, 32(3): 70-86.
[23] Li X R, Jilkov V P.Survey of Maneuvering Target Tracking.Part I: Dynamic Models[J].IEEE Transactions on Ae- rospace and Electronic Systems, 2003, 39(4): 1333-1364.
[24] Mahler R.Statistical Multi-source Multi-target Informat- ion Fusion[M].Norwood, MA: Artech House, 2007.
[25] Mahler R.PHD Filters of Higher Order in Target Number[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.
[26] Vo B N, Ma W K.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Transactions on Signal Processing, 2006, 54(11): 4091-4104.
[27] Vo B, Cantoni A.The Cardinality Balanced Multi-Target Multi-Bernoulli Filter and Its Implementations[J].IEEE Trans.on Signal Processing, 2009, 57(2): 409-423.
[28] Mahler R.CPHD and PHD Filters for Unknown Backgrounds, II: Multitarget Filtering in Dynamic Clutter[C]// Proceedings of SPIE Sensors and Systems for Space Applications III, Orlando, FL, USA: SPIE, 2009.
[29] Vo B, Ma W.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Transactions on Signal Pro- cessing, 2006, 54(11): 4091-4104.
[30] Clark D, Vo B, Bell J.GM-PHD Filter Multi-target Trac- king in Sonar Images[C]//Processings of Signal Process- ing, Sensor Fusion , and Target Recognition XV, Orlando (Kissimmee), FL, USA: SPIE, 2006.
[31] 陈里铭.基于随机有限集的多目标跟踪方法研究[D].大连: 大连理工大学, 2013.
[32] 连峰.基于随机有限集的多目标跟踪方法研究[D].西安: 西安交通大学, 2009.
[33] 秦永.基于随机有限集目标跟踪算法研究[D].武汉: 华中科技大学, 2013.
[34] 李翠芸, 王荣, 姬红兵.基于变分贝叶斯势均衡多目标多伯努利滤波的多扩展目标跟踪算法[J].控制理论与应用, 2015, 32(2): 187-195.Li Cui-yun, Wang Rong, Ji Hong-bing.Based on Variable Decibel Equilibrium Multi-objective Bernoulli Filter, Multi Extended Target Tracking Algorithm[J].Control Theory and Application, 2015, 32 (2): 187-195.
[35] Vo B T, Vo B N, Hoseinnezhad R, et al.Multi-Bernoulli Filtering with Unknown Clutter Intensity and Sensor Fi- eld-of-view[C]//Proceedings of IEEE 45th Annual Conference on Information Sciences and Systems, Baltimore, America: IEEE, 2011.
[36] Vo B T, Vo B N, Hoseinnezhad R.Robust Multi-Bernoulli Filtering[J].IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 399-409.
[37] Mahler R, Vo B T.An Improved CPHD Filter for Unknown Clutter Backgrounds[C]//Proceedings of SPIE Signal Proce- ssing, Sensor/Information Fusion, and Target Recognition XXIII.Baltimore, Maryland, USA: SPIE, 2014.
[38] Georgescu R.Willett P.The GM-CPHD Tracker Applied to Real and Realistic Multistatic Sonar Data Sets[J].IEEE Journal of Oceanic Engineering, 2012, 37(2): 220-235.
[39] Beard M, Vo B-T, Vo B-N, et al.Arulampalam, A Partially Uniform Target Birth Model for Gaussian Mixture PHD/ CPHD Filtering[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2835-2844.
[40] Mahler R.Proceedings CPHD Filters for Unknown Clutter and Target-birth Processes[C]//Signal Processing, Sensor/In- formation Fusion, and Target Recognition XXIII.Baltimore, Maryland, USA: SPIE, 2014.
[41] Vo B N, Vo B T.Random Finite Set Multi-target Trackers: Stochastic Geometry for Space Situational Awareness[C]// Proceedings of Signal Processing, Sensor/Information Fusion, and Target Recognition XXIV: SPIE, 2015.
[42] Beard M, Vo B T, Vo B N.Bayesian Measurements Using Labelled Random Finite Multi-target Tracking with Sets [J].IEEE Transactions on Merged Signal Processing, 2015, 63(6): 1433-1447.
[43] Beard M, Vo B-T, Vo B-N.Bayesian Measurements Using Labelled Random Finitemulti-target Tracking with Sets [J].IEEE Transactions on merged Signal Processing, 2015, 63(6): 1433-1447.
[44] Hoffman J, Mahler R.Multitarget Miss Distance Via Optimal Assignment IEEE Transactions on Systems[J].Man and Cybernetic, 2004, 34(3): 327-336.
[45] Schuhmacher D, Vo B T, Vo B N.A Consistent Me-tric for Performance Evaluation of Multi-object Filters[J].IEEE Transactions on Signal Processing, 2008, 56(8): 3447- 3457.
[46] Nagappa S, Clark D E, Mahler R.Incorporating Track Uncertainty into the OSPA Metric[C]//14th International Conference on Information Fusion, Chicago IL, USA: IEEE, 2011: 1-8.
[47] Ristic B, Vo B N, Clark D, et al.A Metric for Performa- nce Evaluation of Multi-target Tracking Algorithms[J].IEEE Transactions on Signal Processing, 2011, 59(7): 3452-3457.
[48] He X, Tharmarasa R, Kirubarajan, et al.A Track Quality Based Metric for Evaluating Performance of Multi-target Filters[J].IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 610-616.
Present Situation and Prospect of Underwater Multi-Target Tracking Technologies
ZHANG Si-yu, HE Xin-yi, ZHANG Chi, ZHU Lin, CHEN Shuang
(Naval Research Academy, Beijing 100161, China)
Aiming at the unfavorable factors, such as the complexity of underwater hydrological conditions and the relatively small action distance, the key underwater multi-target tracking technologies based on respective data association and random finite set are discussed according to different principles of tracking filtering algorithms.The target motion models, tracking filtering algorithms and its applications status are expounded.The performances of two multi-target tracking technologies are analyzed.Three kinds of technical bottlenecks are analyzed, including the uncertainty of observation information due to failing to report and false alarm, the uncertainty of target number and motion state change in tracking process, and the poor real-time performance of tracking algorithm.The advantages of establishing a unified random finite set framework to describe the tracking problem and solve these bottlenecks are emphasized.Further, according to the requirements of operational application and ocean development, the development direction of underwater multi-target tracking technology is prospected to provide a reference for relevant researchers.
underwater multi-target tracking; data association; random finite set
TJ630.34; TN953
R
2096-3920(2018)06-0511-10
10.11993/j.issn.2096-3920.2018.06.001
2018-05-28;
2018-12-07.
张思宇(1992-), 男, 在读硕士, 主要研究方向为鱼雷自导与水声信号处理.
张思宇, 何心怡, 张驰, 等.水下多目标跟踪技术现状与展望[J].水下无人系统学报, 2018, 26(6): 511-520.
(责任编辑: 杨力军)
