基于互信息的大坝安全分析因子提取方法

高 磊，花胜强，陈 意，郑健兵

（南瑞集团公司（国网电力科学研究院），江苏 南京 211106）

基于回归建模的统计方法是目前大坝变形监测分析的主要手段之一，而因子空间和样本质量决定了回归统计的精度上限，选用合适的回归模型和算法只能逼近该上限。通常，在对大坝变形进行分析时会选取多个回归因子，如多个承前时段内水头的1—4次方值及温度值，多个周期的温度谐波因子，以及多种函数的时效因子。但是由此也衍生了一系列问题，首先，高维度下数据处理的时空复杂度剧增；其次，非相关因子及因子间互相关性会严重干扰回归分析的精度，降低模型的泛化能力和可解释性；最后，不同因子的采样周期差异、数据的非标准化表示等都会影响模型的可信度。因此，如何处理和抽取合理的回归因子，对基于统计方法的大坝变形监测分析具有决定性的意义[1-3]。

1 行业现状

目前业界内变形分析的因子抽取，普遍是基于主成分分析、独立成分分析、典型相关性分析及偏最小二乘回归分析的原理进行抽取和变换的，其主要缺点包括[4-7]：主成分分析、独立成分分析侧重于因子侧的最大化信息表述和抽取，典型相关性分析侧重于效应量和因子的相关性最大化，都不够全面；典型相关性分析和偏最小二乘回归分析都只能考察变量的线性相关性，对于非线性系统则容易失真；数据的预处理也极为重要，如果对未经降噪、去量纲、时序对齐等预处理的因子样本直接进行统计分析，那分析结论的精度通常是不可接受的。

通过以上可以看出，行业内目前普遍采用的因子抽取和变换方法都存在着一定的不足和缺陷，影响了大坝安全分析后续工作的进一步展开。

2 技术方案

为克服以上这些问题，首先通过降噪、归一化和测次对其进行数据预处理，为后续的因子抽取提供可信的样本基础；其次，通过综合最大化因子的方差及变形效应量和因子的相关性，而不是单纯的因子主成分分析，使得因子的抽取更为合理；最后，使用基于互信息而非协方差的相关性检验，避免了仅能衡量线性相关的局限性，进一步提高因子抽取的精度，为后续大坝安全监测的成因分析和回归预测，提供了更为全面和精密的基础，详细技术方案流程如下：

2.1 基于3σ准则的降噪和归一法的去量纲处理[8-11]

原始观察样本中的粗差对于后续的统计分析可能会有极大的影响，甚至使得分析失效，例如因子归一化、某些分类和回归算法对于离群点类的粗差比较敏感，因此应首先去除离群点，本方法采用3σ准则过滤离群点。

根据每个因子的原始样本序列，计算出其均值μ和标准差σ，然后遍历序列的每一个原始测值V，如果满足：|V-μ|≥3σ，即判定该值为离群点，予以剔除。

接下来对每个因子进行归一化以去掉量纲。对于某因子的测值序列，进行变换如下：V’=（V-Vmin）/（Vmax-Vmin），其中，V’为变换后的新测值，V为原始测值，Vmin为本序列中原始测值中的最小值，Vmax为本序列中原始测值中的最大值。

2.2 基于时效的测次对齐

实际大坝安全监测中，变形效应量和各个环境因子难以保证完全同步测量，存在测量时序错位的问题。因此，寻找并匹配变形效应量和各个因子的测值，从而组成一个完整的测次，使得该测次内所有变量的时间差都在有效的时间间隔内，并使得总时间跨度最小，这样可以得到较佳的样本质量。

2.3 基于主成分和互相关最优的因子抽取[12-18]

互信息是两个变量间相关性的度量，表示两个变量间共有信息量的程度，不同于协方差，互信息可以衡量各种关系的相关性。两个变量X和Y的互信息I（X；Y）如下：

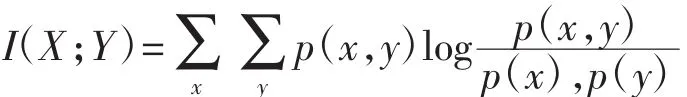
其中，p（x，y）是X和Y的联合概率分布函数，而p（x）和p（y）分别是X和Y的边缘概率分布函数。

令单位向量u为因子矩阵X的第一主成分的转换系数，则目标是要主成分Xu的方差Var（Xu）、变形效应量Y与主成分Xu的相关性综合最大，考虑二者的协方差Cov（Y，Xu）：

即转化为求二者的协方差最大，其中Corr（Y，Xu）为二者的皮尔逊相关系数。此外，协方差计算的是两个变量的线性相关程度，非线性的相关性通过协方差难以挖掘出来。考虑到互信息系数能表征两个变量间的非线性相关性，本文使用互信息I来表征其相关性，所以目标函数形式化表述为：

引入拉格朗日乘子，得到Γ=I（Y，Xu）-λ（uTu-1）/2，两边对u做偏导，即可转为对互信息矩阵的本征值和本征向量的求解问题，根据本征值的降序排列，可得到对应的本征向量集合，此即为因子的各个主成分转换向量。

2.4 降维并形成最终因子抽取的系数转换矩阵

对于第k个主成分转换向量，定义其主成分贡献率为δk：

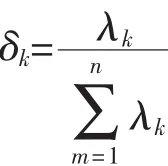
式中，λk为第k个主成分转换向量对应的本征值，n为因子的总数，也是主成分转换向量的总数。

根据λk由高到低的顺序，依次累加其对应的δk，当总和占全部δk总和的98%以上时候，即停止选择，则之前所有入选的对应的δk主成分转换向量集合，即为最终的因子抽取的转换矩阵。

3 算例

以澜沧江某混凝土坝2000—2015年自动化沉降观测资料为例，分别建立原始全回归模型，偏最小二乘回归模型和基于本方法改进的全回归模型。影响沉降的因子包括库水位H、气温T、时效t等，本次实例选取因子为当日、前两日、前3～5日、前5～10日的平均水位H、平均水位的平方值H2、平均水位的立方值H3、平均水位的四次方值H4、气温T、时效的自然对数值ln（t），来组成原始因子矩阵，以matlab程序作为开发环境和宿主程序，拟合结果如下：运行全回归拟合，得复相关系数为0.923 3，剩余标准差为0.613 3；运行偏最小二乘回归拟合，得复相关系数为0.798 1，剩余标准差为0.702 4。运行基于本方法改进的全回归模型，得复相关系数为0.808 3，剩余标准差为0.673 4。

进一步分析模型可以发现，全回归分析虽然针对样本的拟合精度最高，但是从物理成因上无法解释，如水位因子的系数出现负数，常数项值过大，这些都违反了大坝性状分析基础成因理论，纯粹为拟合方程，不能用于实际分析和预测；偏最小二乘回归和本方法改进的回归模型都较好的克服了上述缺陷，模型系数相对合理，也符合实际，但是本模型无论是在拟合阶段，还是在后续的验证阶段，都能取得相对偏最小二乘回归较优的拟合精度，体现出了其稳健性好，鲁棒性强，对客观实际描述更为恰当。

虽然本实例采用的验证方法比较简单，因子的选择和建模结果的理论分析也有较大的改善空间，但也能从某个方面显示出本方法的实用性，随着分析研究的不断深入，希望本方法能对研究和分析水工建筑物实际性态状况起到良好的辅助作用。

4 总结

本文提出了一种大坝变形分析中因子抽取和转换的方法。首先，基于3σ准则和归一法对因子进行降噪和去量纲处理；其次，基于指定的有效时间间隔进行各个因子的测次对齐；再次，基于变形效应量和因子的主成分的互信息最大原则，依次抽取因子的主成分向量；最后，按照主成分贡献率从大到小的规则对主成分向量排序，并按照98%的主成分贡献率总和标准抽取并组合得到最终的因子转换矩阵。通过算例验证表明，本方法提取后的因子空间对于后续大坝安全监测的成因分析和回归预测，提供了更为全面和精密的基础。