基于充电电压均值的锂离子电池RUL估算方法
2019-01-08孙晓艳
孙晓艳, 彭 力
(1. 无锡职业技术学院 控制技术学院, 江苏 无锡 214121; 2. 江南大学 物联网工程学院, 江苏 无锡 214121)
0 引 言
锂离子电池由于具有较高的能量密度、 超长使用寿命和高电压输出等诸多优点而越来越受到市场的青睐[1]. 同时, 锂离子电池的特点也包括具有非常复杂的电化学特性和非线性特点, 在不断地充放电循环使用后, 电池的容量会表现出衰减特性, 同时端电压输出也会降低, 这个现象可以描述为电池老化. 当电池老化到一定程度, 就不能再对相关设备可靠供电, 如果处理不及时, 将会对设备和企业造成严重的不良后果, 因此, 如何精确地预测剩余寿命(Remaining Useful Life,RUL)问题成为锂离子电池应用中的重要研究方向.
锂离子电池的RUL预测方向主要包括基于数据驱动和基于模型驱动的预测方法[2]. 基于数据驱动方向的RUL预测的主要问题在于如何选择具有良好代表性的特征变量, 这些变量来自于直接获得的物理量或者经过处理的物理量, 包括:端电压、 回路电流、 电池表面温度、 电池内阻等, 然后找出相应算法以其中的一些特征变量来预测容量. 基于数据驱动的预测算法中包括神经网络模型(Artificial Neural Network)、 支持向量机(Support Vector Machine)、 相关向量机(Relevance Vector Machine)和粒子滤波(Particle Filter)等等. 而基于模型驱动方向的RUL预测的主要问题在于怎样根据锂离子电池的一些外部特征数据建立较为精确的退化模型来描述电池的老化过程, 主要包括物理化学模型和数学模型. 基于模型驱动的预测方法中的数学模型主要包括多项式模型和指数模型等, 然后以相关算法辨识模型中的参数来表示电池的退化模型, 从而预测RUL. 文献[3]中用自适应神经网络作为预测模型, 选取电池的阻抗作为输入变量, 选取训练数据训练模型, 最后用训练好的模型预测RUL. 文献[4]中用最小二乘支持向量机作为预测模型, 选取电池温度以及充放电倍率作为输入变量, 取得了较好的预测效果. 文献[5]中选用RVM作为预测模型, 输入变量的选择上同样使用了等压降时间序列, 有效提高了RUL的预测精度. 文献[6]中用粒子滤波结合支持向量机来预测RUL, 有效提高了RUL的估计和预测能力. 文献[7]中考虑了两个电阻和温度因素, 并且使用了两个RC回路, 建立锂离子电池的容量退化模型, 获得了较好地RUL估计结果. 文献[8]中使用了一个阻抗值和一个RC网络组成的串联模型并考虑温度因素的影响来构建电池的容量退化模型, 也能够较好地描述电池的容量衰减. 相对于数学模型, 前面提到的物理化学模型结构较为复杂. 文献[9]中采用了指数模型描述锂离子电池的容量衰退过程, 最后预测失效阈值并计算RUL. 文献[10]中采用了锂离子电池放电过程中的温度数据, 联合充放电循环次数N建立了一阶电池容量退化模型, 估计的结果表明, 获得了较高的估计精度.
基于数据驱动的预测方向中, 挖掘电池数据之间的隐含关系容易受到实验数据的不完整性的影响, 并且由于电池个体间差异, 该方法的鲁棒性和适应性也较差. 而基于模型驱动的方向中, 物理化学模型虽然能更精确地描述电池的内外部特性, 但是结构非常复杂. 数学模型具有较为简单的结构, 选择好相应的特征量, 建立好适当结构模型, 能够较为精确地预测RUL. 文献[10]中选用了放电温度速率来预测RUL, 获得了较高的精度, 但是放电过程容易受到负载的影响, 数据变化具有多样性, 所以这种方法并不适合其他放电状况下的锂离子电池.
本文提取了数据具有较好稳定性的锂离子电池充电数据中的电压数据, 对充电电压数据进行处理, 获得了每个充电过程中的电压平均值, 以充电电压平均值作为特征量, 和充放电循环次数N构成二元模型, 最终构建锂离子电池的二阶多项式退化模型.
1 锂离子电池退化过程及数据处理分析
锂离子电池数据来自于美国宇航局(NASA)中的实验数据, 包括锂离子电池的充电数据、 放电数据和阻抗实验数据. 考虑到不同放电过程数据不一致性对预测的影响, 所以选用数据均采用充电过程中的数据. 充电过程的实验数据包含了充电电压数据、 充电电流数据、 电池温度数据、 时间序列以及阻抗数据.
锂离子电池的外部可直接测量的物理量包含端电压、 回路电流和电池温度. 而电池在经过不断充放电循环后, 电池表现为逐渐衰老的特性, 直接表现为电池内部阻抗的变化和电池满容量的衰减. 在导致这些直接量阻抗和容量变化的同时, 也对外部的可直接测量物理量产生影响, 如在相同倍率的充电模式下, 电池的电压变化曲线随着充放电次数N的增大会在恒流充电阶段相应上移, 温度曲线也有变化. 随着充放电过程的不断循环, 电池外部的温度曲线和电压曲线都有明显的变化. 从温度变化曲线可以选择可能的输入变量, 它们分别是充电过程最高最低温差Tem_diff, 充电过程温度均值Tem_mean, 充电过程温度上升的最大斜率Tem_slope. 而从电压曲线中可以选择可能的输入变量有充电过程电压均值V_mean和充电过程点压上升最大斜率V_slope.
从NASA获得的原始数据中, 对充电数据进行相关处理.
其中,Tem_diff的定义如式(1). 其中charge_T是充电过程温度数据集, max为求最大值函数, min为求最小值函数.
Tem_diff=max(charge_T)-
min(charge_T).(1)
Tem_mean的定义如式(2). 其中mean为求平均值函数.
Tem_mean=mean(charge_T).(2)
Tem_slope的定义如式(3). 其中diff为求斜率函数. Matlab中的diff函数的求解过程如式(4), 表示当前时刻的采样点减去上一时刻的采样点, 而对于数据集来说, 就是所有后一个采样点减去前一个采样点获得的数据组成的集合.
Tem_slope=max(diff(charge_T)),(3)
diff(charge_T)k=(charge_T)k-
(charge_T)k-1.(4)
V_mean的定义如式(5). 其中charge_V是充电过程电压数据集.
V_mean=mean(charge_V).(5)
V_slope定义为如式(6).
V_clope=max(diff(charge_V)).(6)
除了上述五个变量外, 还有和容量衰减相关的欧姆内阻Re和电化学反应阻抗Rct.
2 锂离子电池退化模型构建
2.1 Pearson相关系数
为了分析上节内容获得的7个变量与容量C之间的相关程度, 采用Pearson相关系数求它们之间的相关性.
设两个变量X和Y, 那么两个变量之间的Pearson相关系数可以用式(7)表示, 式中的N表示变量取值的个数.
(7)
求得的Pearson相关系数值在-1到1之间, 绝对值越大, 表明相关性越强. 其中正值表示正相关性, 负值表示负相关性. 绝对值在0.8~1之间表示两个变量之间具有极强相关性, 而零表示无相关性.
2.2 特征值的选取
为了能够选择合适的特征量来表征电池的容量老化过程, 对上节中的7个可能变量分别和容量C求Pearson相关系数, 其值如表 1 所示.
从表格中筛选出具有极强Pearson相关系数的变量, 舍弃较小Pearson相关系数的变量, 此时保留的变量有:Tem_diff,V_mean,Re和Rct共四个变量. 但由于Re和Rct是两个非直接获得量, 是通过相关辨识方式进行辨识获得的参数, 而辨识获得的参数存在辨识值准确性低和非直接性等缺点, 所以舍弃, 选择具有容易获得的直接变量Tem_diff和V_mean.
在两个变量Tem_diff和V_mean中, 经过搭建基于容量的退化模型进行仿真验证, 虽然两个变量都和容量C之间有着接近的极强负相关性, 但是基于V_mean的退化模型有着较好的拟合效果, 因此, 特征值最终选择V_mean, 即充电过程中的电压平均值.
2.3 锂离子退化模型构建
由于V_mean值能够从间接测量的电压值处理中得到, 并且和电池的容量之间具有极强的线性相关性, 因此作为特征值使用. 同时, 为了描述基于模型的容量退化模型, 估计电池的RUL, 将充放电循环次数N考虑进去, 同变量V_mean构成二元容量退化模型. 显然, 建立基于变量V_mean的多项式模型更为恰当. 这里以V_mean的最高次幂作为容量退化模型的阶数, 结合充放电循环次数N构建一阶, 二阶,…,n阶容量退化模型, 分别如式(8)~式(10)
C=X1*V_mean+X2*N+X3,(8)
C=X1*V_mean2+X2*V_mean+
X3*N+X4,(9)
C=X1*V_meann+X2*V_meann-1+…+
Xn*V_mean+Xn+1*N+Xn+2.(10)
不同阶次的容量退化模型的回归精度不一样, 为了确定具有最高回归精度的容量退化模型的阶数, 这里以NASA中的B0005#电池数据进行仿真测试. 容量退化模型的中相关参数采用最小二乘拟合函数进行确定. 拟合的精度效果采用均方根误差RMSE进行进行评定, 均方根误差公式如式(11)所示. 均方根误差越小, 越接近于零, 说明拟合的效果越好.
(11)
分别对一阶容量退化模型、 二阶容量退化模型、 三阶容量退化模型和四阶容量退化模型进行拟合, 拟合结果图如图 1 所示, 求得的RMSE值如表 2 所示.

表 2 不同阶退化模型的RMSE

图 1 不同阶退化模型拟合结果Fig.1 Fitting results of different order degenerate models
从图 1 可以直观地看出, 除了一阶容量退化模型无法跟踪真实容量的变化过程外, 其他三种阶数的容量退化模型都能比较好地跟踪容量退化趋势, 且能够跟踪容量的自充电现象. 从表 2 的RMSE误差可以看出, 基于一阶容量退化模型的误差较大, 不宜采用, 从二阶模型开始, 误差基本相同, 为了不增加容量退化模型的复杂度, 又能保证退化模型的精度, 显然退化模型的阶数选择二阶最为合适.
从前面的分析可以得出, 最终选择如式(9)所示的容量退化模型作为预测模型.
图 2 为RUL预测流程图.
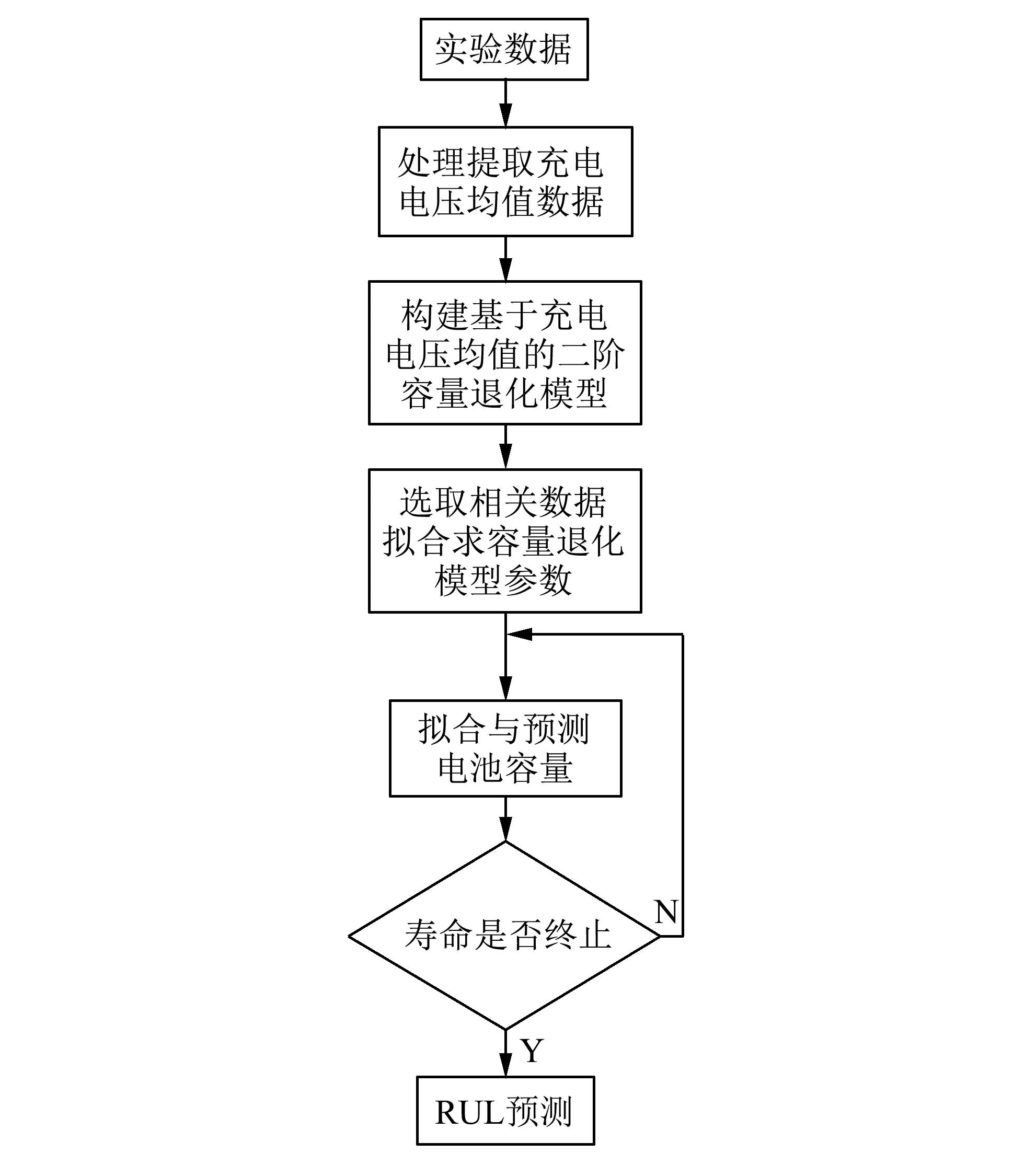
图 2 RUL预测流程图Fig.2 RUL prediction flow chart
3 仿真测试与结果分析
为了验证基于充电电压均值的二阶容量退化模型估算RUL的精度和预测能力, 对其在MATLAB中进行仿真验证. 为了能够更好地证明基于充电电压均值的二阶容量退化模型对锂离子电池具有普遍的适用性, 分别选取了NASA中的B0005#, B0006#和B0018#共三个电池进行验证. 针对不同应用场合下的锂离子电池, 其失效阈值也不尽相同, 国际标准规定为锂离子电池的SOH为80%时, 表示该电池已经寿命终止(End of Life,EOL), 不再使用. 如图 3 所示, 不同电池的失效阈值不同, 根据NASA中给出的实验数据, 这里B0005#电池的失效阈值定义为70%; B0007#电池的失效阈值定义为75%; B0018#电池的失效阈值定义为74%. 对于RUL的预测, 对B0005#, B0006#具有166次充放电循环次数的三个电池的前70个充放电循环进行拟合求参数, 并对后面的数据进行预测输出, 而对于B0018#共有130次充放电循环次数的锂离子电池, 选取前50次充放电循环次数的数据进行拟合求参数, 对剩余的数据进行预测输出.

图 3 不同电池的容量退化曲线Fig.3 Capacity degradation curve of different batteries
如图 4 为B0005#, B0007#和B0018#三个电池在第70个充放电循环次数时的预测曲线, 分别对应图4(a)~图4(c). 从图4(a)中可以看出, B0005#电池在拟合阶段具有较好的拟合效果, 能够拟合锂离子电池的自充电过程. 在70个充放电循环次数后的预测阶段, 也显示出了较好的预测能力, 其失效容量阈值为1.320 Ah, 且在预测RUL时, 基于充电电压均值的二阶退化模型的实际寿命终止点和预测寿命终止点基本重合; 从图4(b) 中可以看出, B0007#电池在拟合阶段有着较高的精度, 在70个充放电循环次数后的预测阶段也有着较好的预测效果, 在预测的寿命终点时偏差和B0005#电池比较有所变大. 从图4(c)中可以看出, B0018#电池的拟合状况和预测状况同图4(b)相比有着类似的过程.
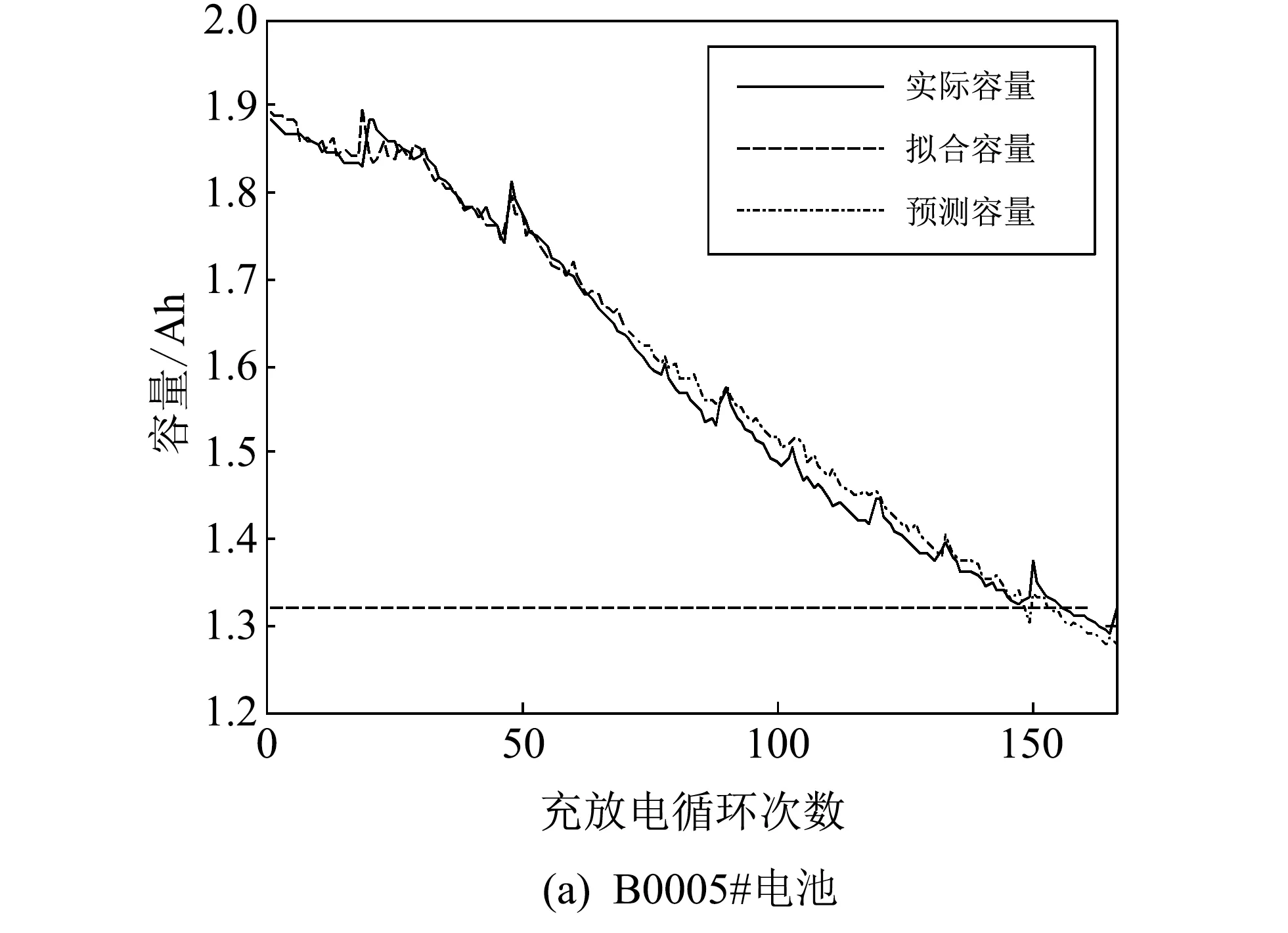


图 4 三个电池70个充放电循环次数预测曲线Fig.4 Prediction curves of three batteries in 70 cycles of charge and discharge cycles
如图 5 所示为B0005#, B0007#和B0018#电池在70次充放电循环次数时的预测误差曲线. 从图5(a) 可以看出, B0005#电池在拟合阶段和预测阶段表现为较稳定的趋势, 整个过程的误差都较小. 从图5(b)中可以看出, B0007#电池在拟合阶段误差都在±2%以内, 但在预测阶段, 误差有所增大, 但最高不超过4%. 从图5(c)中可以看出, B0018#电池的拟合误差都在±2%以内, 预测阶段的误差最大不超过5%, 同样取得了较好的预测结果.
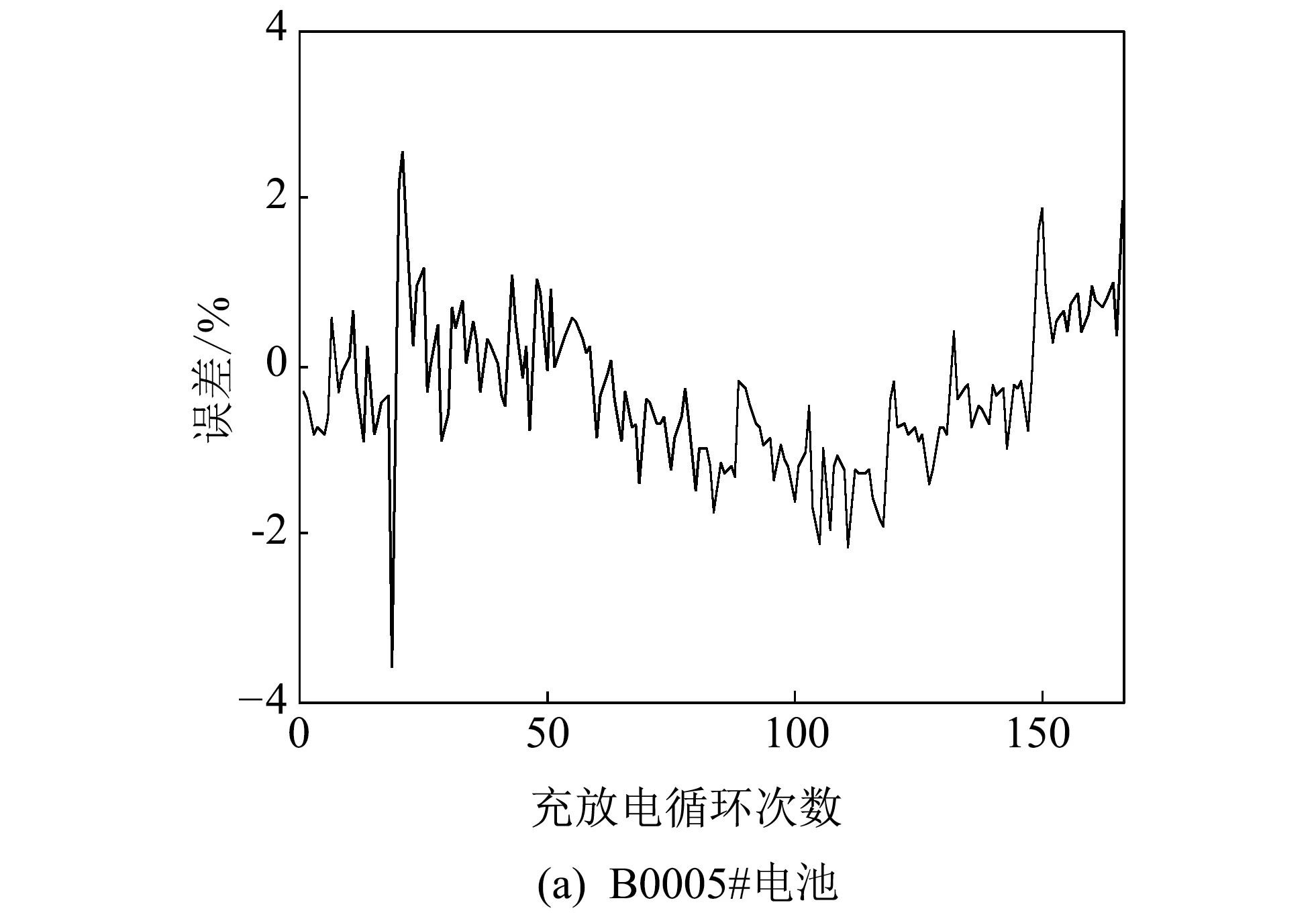


图 5 三个电池70次充放电循环次数预测误差曲线
表 3 为B0005#电池, B0007#电池和B0018#电池的EOL和RUL预测结果对比. 相比较而言, 所提方法和文献[10]中的方法对电池B0005#的预测结果基本一致, 两种方法对B0007#电池的预测都比B0005#电池的预测结果要差, 误差都是16次. 但是本文的方法的优点在于:文献[10]中的方法基于模型的RUL预测用到的是放电过程的温度数据, 放电过程受放电条件的影响, 具有不稳定性, 而本文所提方法中用到的是基于充电过程中的电压平均值, 充电过程电压具有较好的一致性, 并且同样能够达到文献[10]的预测精度.
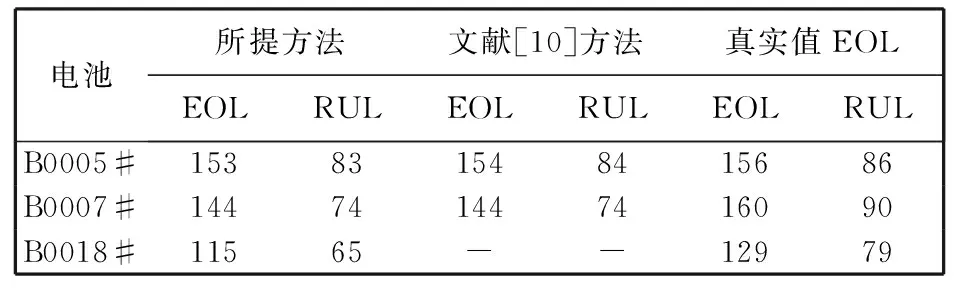
表 3 EOL和RUL预测结果对比
4 结 论
本文以充电过程中的电压为原始数据, 对充电过程电压求均值, 并建立以V_mean和充放电循环次数二元容量模型, 以V_mean的最高次幂作为电池容量退化模型的阶数, 建立了锂离子电池的二阶容量退化模型, 并进行了仿真分析, 得出如下结论:
1) 基于充电电压均值的二阶容量退化模型对锂离子电池的RUL预测具有较好的精度; 为锂离子电池的RUL预测提供了一种新思路.
2) 实际锂离子电池即使是同一批次生产的, 也会存在个体差异, 而基于充电电压均值的二阶容量退化模型对不同锂离子电池的RUL预测均具有较好的适应性; 这为改模型能应用到实际中提供了保障.
