基于负荷变化的主动配电网动态电压协调控制
2019-01-08李红娟
李红娟, 徐 敏, 张 皓
(1.南昌大学 信息工程学院, 江西 南昌 330031; 2. 国网江西省电力公司上饶供电分公司, 江西 上饶 334000)
随着分布式电源的大量接入, 传统配电网的可控性逐渐增加[1], 同时给配电网运行带来巨大挑战[2], 主动配电网成为发展的必然趋势, 与传统配电网相比, 主动配电网具有一定的可控性和随机性[3]. 分布式电源无功出力的调节可以提高主动配电网的电压质量[4], 有助于促进可再生能源的消纳, 但也给电压控制带来一定困难. 目前已有主动配电网电压控制的相关研究, 文献[5]把系统的控制区域分为自治控制区域和协调控制区域两部分进行电压分层协调控制; 文献[6]利用局部测量数据和通信, 通过分布式计算实现对全局电压的控制; 文献[7-8]建立高维多目标无功电压控制模型, 运用智能算法求解帕累托解集, 提出具体的控制策略. 上述研究没有考虑负荷变化, 是对主动配电网的静态电压控制, 并且对于建立的多目标模型, 在得到Pareto解后, 根据决策者的经验选择决策方案, 没有提供相关依据.
针对上述问题, 本文在考虑负荷变化的基础上, 以电压偏差、 网损、 系统最低电压作为目标函数, 采用灰狼算法对动态电压控制模型求出Pareto解集. 采用几何上“重心”的思想选择目标函数的公共区域解, 优先考虑系统最低电压, 在Pareto解集中选出电压控制策略, 提高主动配电网的运行水平和经济性.
1 配电网负荷
1.1 负荷介绍
系统中所有电力用户的用电设备消耗的电功率总和是电力系统的负荷. 配电网的负荷按用途分三类: 工业负荷、 商业负荷、 民用负荷[9]. 配电网的各类用电设备在运行时负荷变化很大, 因此在进行主动配电网电压控制时, 必须考虑负荷变化. 但是负荷的划分段数越多, 数据越多, 负荷模型[10]的计算时间越多, 电压控制的效果也会受到影响, 因此本文提出根据负荷曲线[11]对负荷进行数据处理.
本文采用日负荷曲线, 根据工业负荷曲线、 商业负荷曲线、 民用负荷曲线各自的特点, 将负荷分为最大负荷、 最小负荷、 一般负荷. 最大负荷定义为一天24 h节点最大负荷时间段内的平均值, 最小负荷定义为一天24 h节点最小负荷时间段内的平均值, 一般负荷定义为剩余时间段内负荷的平均值. 在计算目标函数时, 根据三种负荷方式分别占整天(24 h)负荷的百分比进行综合计算.
1.2 动态负荷处理
动态电压控制是根据实际配电网的负荷变化进行优化提出控制策略, 用于静态电压控制的方法已经不适用于动态控制. 如果根据每时刻的负荷进行电压控制, 不仅操作频繁而且会减小设备寿命, 因此本文考虑对负荷进行动态处理.
首先需要明确负荷类型以及相应类型的典型日负荷曲线, 然后根据该节点的最大负荷进行负荷处理, 每种类型的每个节点的每个时刻的负荷计算公式如下
S1=Pmax,(1)
S2=Qmax,(2)



2 主动配电网动态电压控制模型
2.1 数学模型
本文以电压偏差、 网损、 系统最低电压为目标函数的数学模型, 分布式电源和传统无功补偿装置出力作为控制变量, 提出电压控制策略.
2.1.1 目标函数
1) 目标函数1: ADN电压偏差和最小
(5)
式中: ΔVt为第t个时刻的电压偏差和;i=1,2,3,…,T,T为配电网节点总数;VN为额定电压;i,j分别为支路的首端和末端节点; ΔVij为支路ij电压降落纵分量;δVij为支路ij电压降落横分量;x为控制变量.
a*ΔVLmax+b*ΔVLmin+c*ΔVlav,(6)
式中:k为三种负荷方式, 最大负荷、 最小负荷、 一般负荷;a,b,c为三种负荷方式占整天负荷的比例, ΔVLmax, ΔVLmin, ΔVlav为三种负荷方式的电压偏差和.
2) 目标函数2: ADN网损最小
(7)
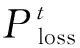
a*PLmax+b*PLmin+c*Plav,(8)
式中:PLmax,PLmin,plav为三种负荷方式的网损.
3) 目标函数3: 最低点电压最高
(9)

a*VLmax+b*VLmin+c*Vlav,(10)
式中:VLmax,VLmin,Vlav为三种负荷方式的系统最低电压.
2.1.2 约束条件
1) 含DG的潮流等式约束条件
(11)
式中:Pi,Qi为输入第i节点的有功和无功功率;PDGi,QDGi为DG向节点i注入的有功、 无功功率;PDi,QDi为节点i处负荷有功、 无功功率;Vi,Vj为节点i,j电压;Gij,Bij和δij、θij为节点i,j电导、 电纳和相角差.
2) 不等式约束条件
Qimin≤Qi≤Qimax,(12)
Vimin≤Vi≤Vimax,(13)
式中:Qimax,Qimin为电容器i最大、 最小无功出力;Vimax,Vimin为节点i电压上下限.
2.2 求解算法——灰狼算法
灰狼算法(Grey Wolf Optimization, GWO)是模拟狼群狩猎行为的一种智能算法. 灰狼群体有严格的社会等级, 将狼群适应度最优的、 次最优的和第三优的记为α,β,δ狼[12], 介绍如下:
1)α,β,δ狼选择机制.α,β,δ狼来自于Pareto解集, Pareto解集用来存放迭代中产生的新Pareto解, 解集大小为N. 当存入的Pareto解的个数大于N时, 由拥挤距离进行选择, 保证Pareto中的解的个数不大于N. 单目标优化利用适应度选择, 适应度最优为α狼, 适应度次最优为β狼, 第三优为δ狼, 多目标优化则根据非支配关系进行分层, 根据拥挤距离进行排序[13], 根据分层排序的结果选择α,β,δ狼.
2) 包围猎物[14]. 包围猎物是狼群捕食的重要过程, 数学模型如下
D=|C·Xp(t)-X(t)|,(14)
X(t+1)=Xp(t)-A·D,(15)
A=2a·r1-a,(16)
C=2·r2,(17)
式中:D为灰狼与猎物之间的距离;t为当前迭代次数;A和C是协同系数的向量;Xp为猎物的位置向量;X为灰狼的位置向量;a在迭代过程中线性变化;r1和r2为[0,1]之间的随机数.
3) 攻击猎物. 猎物的位置是不停变化的, 为了捕捉到猎物, 由适应度较好的三只狼的位置对猎物进行定位, 本文引入动态权重加快算法收敛速度, 具体公式如下
Dα=|C1·Xα(t)-X(t)|,(18)
Dβ=|C2·Xβ(t)-X(t)|,(19)
Dδ=|C3·Xδ(t)-X(t)|,(20)
X1=Xα-A1·Dα,(21)
X2=Xβ-A2·Dβ,(22)
X3=Xδ-A3·Dδ,(23)
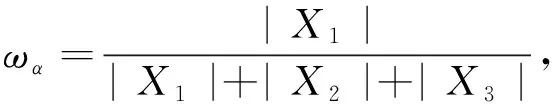


X(t+1)=(ωaX1+ωbX2+ωcX3)/3,(27)
式中:ωa,ωb,ωc为α狼、β狼、δ狼所占的权重.
2.3 基于灰狼算法的计算流程
灰狼算法对数学模型求解得到Pareto解集, 流程如下:
1) 初始化灰狼个体. 对灰狼个体的每一维进行初始化, 每一维变量在其上下限内随机产生.
2) Pareto存档. 对于初始化后的灰狼个体进行分层排序以完成Pareto存档. 具体操作为:对种群中的所有个体根据非支配关系进行分层, 将非支配个体分配为第1层, 并将其从种群中移出; 然后在剩下的种群个体中选出所有的非支配个体分配为第2层, 以此类推直到每一个个体都设定了相应的层级. 然后对每一层的个体依据拥挤度距离进行排序, 处于每一层边界解的拥挤距离为无穷大, 拥挤距离的计算式为
(28)
式中:k为目标函数的个数;Dn为第n个个体的拥挤度距离;Fm,n为第n个个体的第m个目标函数的值;Fm,max,Fm,min分别为第m个目标函数的最大值和最小值.
3) 在Pareto解集中选择狼. 按照Pareto等级选择3个优秀的个体作为狼.
4) 狩猎行为, 每只狼改变一次位置. 根据式(18)~(27)改变狼的位置.
5) 更新Pareto存档. 将得到的新Pareto解添加到Pareto存档重新进行分层排序, 并删除存档中被新解支配的解.
6) 终止条件判断. 判断是否满足终止条件, 不满足的条件下重复第三步, 直到迭代结束得到Pareto解集, 供决策者根据实际情况选择最佳的电压控制策略.
2.4 控制策略
大量研究得到优化解集后, 根据决策者的经验选择决策方案, 针对上述问题, 本文采用几何“重心”的思想. 本文有三个目标函数, 采用三角形重心, 即三角形三边中线的交点. 三角形三边分别代表电压偏差和、 网损、 系统最低点电压, 三条中线分别代表国家标准对电压偏差、 网损、 节点电压规范的合理区间, 重心代表电压控制策略. 选择Pareto解集落在上述三个指标的合理区间内的公共区域解, 同时在出现多个解时, 因电压控制的目的为提高系统电压运行水平, 优先考虑系统最低电压, 该方法避免决策的经验性, 提高决策的合理性和准确性, 具体介绍如下:
1) 首先确定电压偏差、 网损、 系统节点电压的合理范围. 其合理区间根据国家标准和现场实际要求确定.
2) 出现公共区域含有多个解时, 优先考虑系统最低电压, 将系统最低电压最大的一组解作为电压控制策略, 有助于提高系统的电压运行水平.
对多目标决策问题常采用Topsis[15]排序决策法, 但其在构造加权标准化矩阵时, 改变了原评价数据间的关系结构, 不符合权重的使用意义, 会造成不合理的方案选择, 而本文提出的策略避免了权重确定的主观性, 使得评价结果更贴近实际.
综上所述, 灰狼算法运用于主动配电网动态电压控制流程图, 如图 1 所示.

图 1 主动配电网动态电压控制流程图Fig.1 Dynamic voltage control flow chart of active distribution network
3 算例分析
本文采用算例在标准IEEE33节点基础上进行修改, 首端基准电压12.66kV, 18节点接入光伏发电, 最大有功功率120 kW, 功率因数0.999, 该光伏为功率因素不变, 有功无功可调节型; 节点6, 11, 25, 33接入电容器组1,2,3,4, 均有30台, 每台容量40 kvar. 参数设置如下: 最大迭代次数为100, 初始灰狼种群数为20, 依据GB/T12325-2008规定20 kV及以下三相供电, 电压允许偏差为额定电压的±7%. 在进行相关运算时均采用标幺值, 以电压12.66 kV, 功率10 MVA为基值,平衡节点为1, 电压为1.0 pu. 表 1 为IEEE33节点的负荷类型.
根据式(1)~(4)计算各节点负荷值, 然后给出各节点的最大负荷、 最小负荷和一般负荷运行方式下的有功功率和无功功率, 运用灰狼算法求解电压控制模型, 得到Pareto解集, 结果如表 2 所示, 根据上文提出的选择三个目标函数的公共区域解, 优先考虑最低电压的控制策略, 上述系统提出的电压协调控制策略为: 光伏出力为120 kW, 节点6, 11, 25, 33分别投入11, 13, 4, 10台电容器. 以最大负荷方式运行状态验证控制策略, 采用该策略各节点的电压如表 3 所示.

表 1 IEEE33节点的负荷
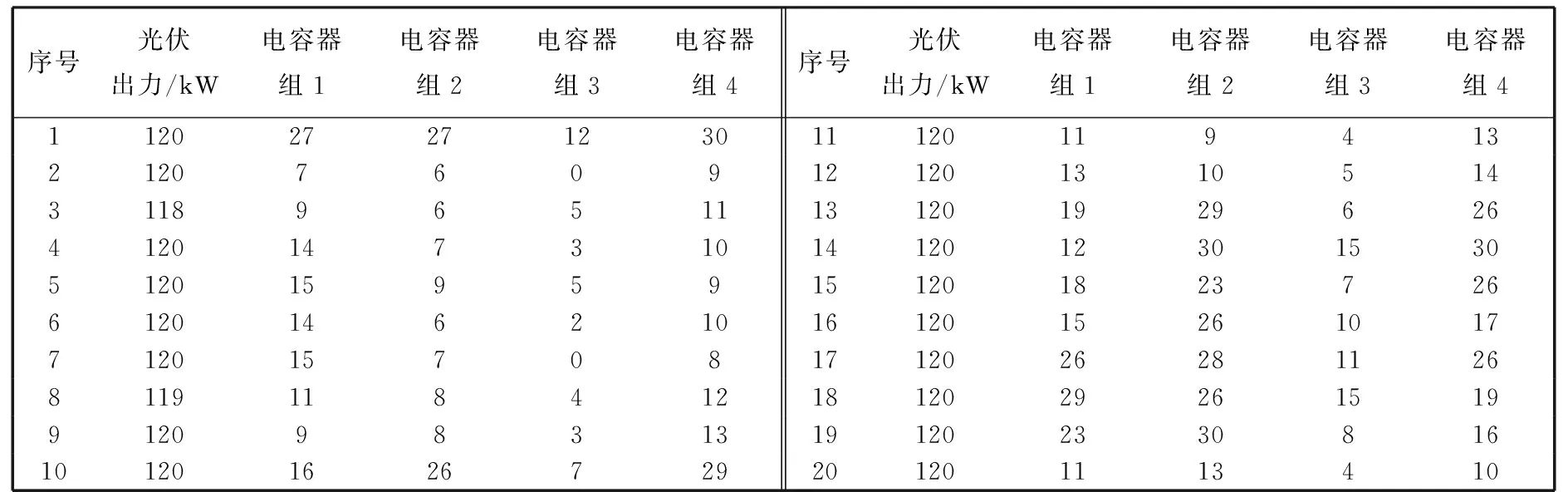
表 2 各组无功补偿装置投入

表 3 优化策略对应的节点电压
由表 2 知, 与文献[14]的多目标粒子群算法(MOPSO)相比, 运用灰狼算法对多目标优化函数搜索得到Pareto解集, 可以保持较好的搜索能力, 得到比较理想的Pareto解集, 并且各分布式光伏出力均接近消纳最大化状态, 与文献[16]提出的电压控制策略中光伏出力相比, 有助于促进和解决分布式电源的消纳问题.
由表 3 知, 在最大负荷运行方式下, 该优化策略使得各节点电压均得到提高, 且各节点电压均满足GB/T12325-2008对电压偏差的要求, 最低点电压由0.921提高到0.944, 具有较好的调压效果.
采用上述调控策略, 在最大负荷运行方式下, 优化前初始状态系统网损为191kW, 优化后系统网损变为138kW, 网损得到了明显的降低, 满足配电网经济运行的要求. 在最大负荷方式下, 其功率需求较大, 上述提出的电压控制策略能够满足要求, 则其他负荷方式下亦能满足要求, 实现配电网经济可靠运行.
4 结 论
从安全可靠性角度出发, 在考虑动态负荷的基础上, 建立以电压偏差最小、 网损最低、 系统最低电压为目标函数的主动配电网动态电压控制模型, 应用灰狼算法协调分布式电源与传统无功补偿装置得到Pareto解集, 选取三个目标函数公共区间, 优先考虑系统最低电压, 在解集中得到最优策略. 结果表明, 提出的优化策略可以实现动态电压协调控制, 避免了负荷变化带来的频繁操作的缺点, 提高了主动配电网运行水平, 同时满足了经济性的要求.
