四极-十六极分区式线型阱中汞离子囚禁仿真研究
2019-01-08王朝全涂建辉崔敬忠
王朝全 涂建辉 崔敬忠
(兰州空间技术物理研究所,真空技术与物理重点实验室,空间量子频标技术核心专业实验室, 兰州 730000)
1 引 言
近年来,随着激光冷却和原子、离子囚禁等各类新技术的成熟和广泛应用,基于新物理原理、新方法的原子钟技术得到了迅速发展。其中,离子阱微波钟是通过加在特定构型电极上的静电、磁场或射频场构成离子阱的作用,将离子囚禁在超高真空的甚小尺度范围内,使离子处于几乎孤立的不受“干扰”的环境,从而增加离子与辐射场的相互作用时间,并且减小多普勒效应的一种新型原子钟。世界上第一台离子阱微波频标是1981年法国LHA实验室的M.Jardion 和C.Audion 在双曲面Paul离子阱中研制成功的。1989年,美国喷汽推进实验室(JPL)首次提出用线型阱代替双曲面阱的方案,开发出了检测区和共振区合一的单区式线型阱,并实现了汞离子的微波钟[1,2]。线型离子阱中汞离子囚禁可以增加囚禁离子的数目,提高信噪比和抑制二级多普勒频移。理论分析表明,对于相同量级的二阶多普勒效应,线型阱可以比双曲面阱多囚禁20倍的离子[3]。1996年JPL又研制出检测区和共振区分离的分区式汞离子微波钟[4]。1999 年JPL首次将多极线型阱应用到了汞离子微波频标中[5]。与四极阱相比,多级阱等效囚禁势相对较宽并且在很大范围内势场平缓,离子云密度较低,离子的相互作用较小,二级多普勒频移将更小。近年来,JPL公司一直致力于研究基于四极-多极分区式线型阱的汞离子星载微波钟[6,7]。根据四极和多极线型阱中离子囚禁的特点可以将微波钟设计为分区式结构,这种设计有两个方面优点:其一,在粒子分布相对集中的四极阱中对离子进行光抽运和信号检测,这将提高光抽运和信号检测效率,在粒子数分布比较稀疏的多极阱中对离子进行微波作用,这将减小离子间的碰撞以及斥力相互作用,从而减小微波钟的二阶多普勒频移,提高其稳定度;其二,单区式的线型阱中,由于光路等装置的存在不利于较好地进行磁屏蔽,而在分区式线型阱中可以对独立的微波共振区较好地进行封闭式电磁屏蔽,以减小外部杂散磁场的影响。另外,基于汞离子囚禁的微波钟由于不依赖于庞大、笨重的激光系统使得它具有重量轻、体积小的特点,非常适合作为下一代星载原子钟,可用于新一代导航系统、深空探测等项目。综上可知,应用于汞离子微波钟的四极-多极分区式线型离子阱具有很高的研究价值。
2 离子阱模型
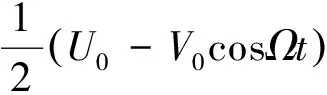
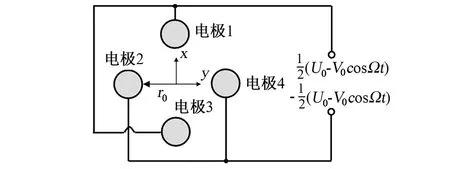
图2 杆电极连接及电压施加方式Fig.2 Arrangement of electrode rods and applying its voltage
3 基本问题模拟
对于四极-十六极分区式离子阱,离子的稳定囚禁参数在四极阱和十六极阱中是不同的。文中首先研究了汞离子在不同囚禁区域时的第一稳定区。在四极阱中分别模拟了Ω1=4.5MHz、Ω2=5.0MHz、Ω3=5.5MHz、Ω4=6.0MHz四种不同射频频率下的第一稳定区,如图3所示。在十六极阱中分别模拟了ΩΙ=11.0MHz、ΩΠ=14.0MHz两种射频频率下的第一稳定区,如图4所示。在图3中可以发现,四极阱中离子的稳定区区域形状均为四边形,且关于直流电压为零对称。稳定区的边界表现为首先随着射频电压幅度增大,直流电压的幅度正负值对称地慢慢变大,当射频电压增大到某个值时直流电压的幅度正负值对称地达到最大值,进而继续增大射频电压,则直流电压的幅度正负值对称地迅速减小。不同杆电极的射频频率下离子稳定区的区域大小也不同,频率越低离子稳定区区域越小,主要表现在杆电极频率越低,稳定区内的最大射频电压越小。尽管如此,比较Ω2=5.0MHz、Ω3=5.5MHz时的稳定区可以发现,对于某个不太大的杆电极射频电压如Vr=200V,频率较低时有更大幅度的直流电压存在于稳定区,而对于某个较大的杆电极射频电压如Vr=300V,频率较高时有更大幅度的直流电压存在于稳定区。我们仿真模拟的四极阱稳定区的这些特征与理论结果相一致。另外,从图4可见十六极阱中离子稳定区有和四极阱稳定区相同的特征,只不过相同结构参数(即杆电极半径、杆电极长度、杆电极到阱中心的距离均相同)下十六极阱中稳定区所要求的杆电极频率更高,例如经验证此时在十六极阱中频率Ω<8MHz情况下基本得不到区域连续的稳定区。另外,稳定区的区域更大,尤其表现为最大的稳定射频电压幅度将变大,例如在图4中射频电压加到500V时,仅仅能模拟出稳定区的一部分。这也说明,相同结构参数下在十六极阱中杆电极电压调节范围更大,而且能够实现更大的势阱深度。
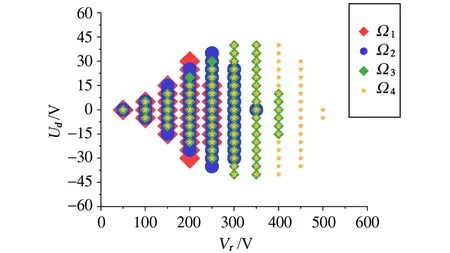
图3 四极阱中汞离子囚禁稳定区Fig.3 Stable region in a quadrupole trap
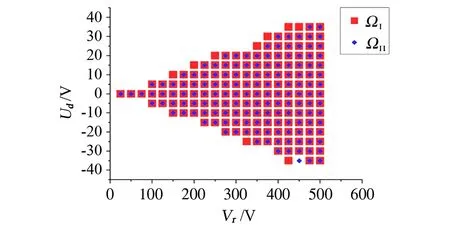
图4 十六极阱中汞离子囚禁稳定区Fig.4 Stable region in a sixteen-pole trap
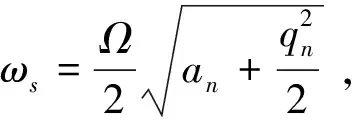

图5 稳定区内离子运动Fig.5 Ion motion in a stable region

图6 杆电极直流电压对离子运动影响Fig.6 Effect of dc voltage on ion motion
然后分别模拟验证了十六极阱中ΩΠ=14.0MHz对应的稳定区内稳定电压Ud=0V、Vr=120V和Ud=-2V、Vr=80V时的离子运动,分别如图7和图8所示。模拟发现,稳定区内的不同稳定电压下虽然离子均能被稳定囚禁,但其运动特征有较大差别,例如图8情况下离子的微运动效应要比图7时大很多。因此在稳定区内寻找优化电压,使得离子微运动效应降低是一项必要的工作。当然,稳定电压的选择除了考虑离子微运动,还要考虑射频加热、功率等问题,因此整体优化稳定电压是一个综合性问题。
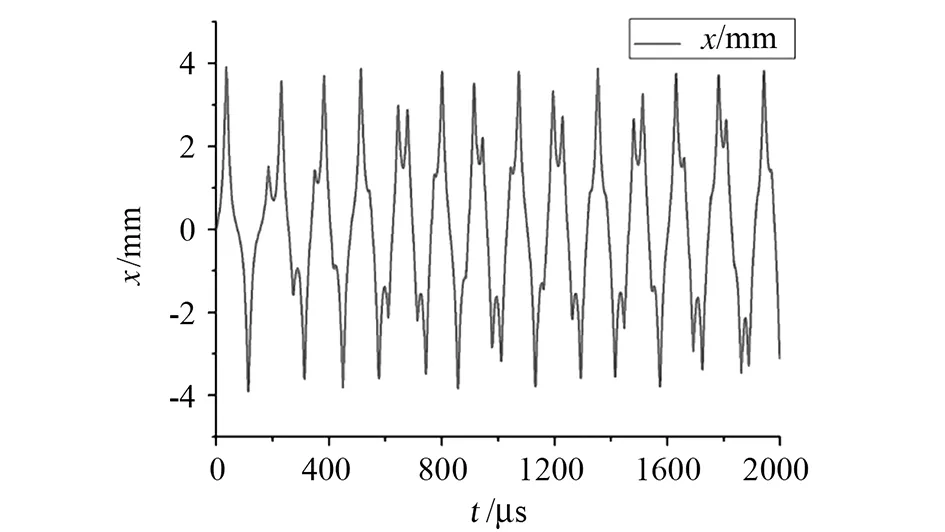
图7 Ud=0V,Vr=120V时离子运动Fig.7 Ion motion for Ud=0V,Vr=120V
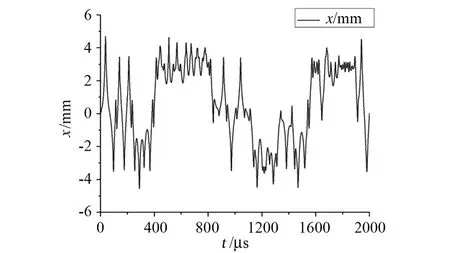
图8 Ud=-2V,Vr=80V时离子运动图8 Ion motion for Ud=-2V,Vr=80V
在相同离子阱几何和电气参数下,由于离子间库伦斥力的存在,囚禁离子的数目不同将产生不同的离子云囚禁体积以及粒子数密度,这将会造成离子的运动速度不同。为了验证这一点,在十六极阱中分别模拟了汞离子数N1=2×107和N2=2×105两种情况下离子在x和z方向的运动轨迹以及速率,如图9所示。模拟发现,在相同囚禁条件下囚禁的离子数目越多,稳态条件下离子的运动范围越大即离子云的囚禁体积越大,例如离子数为N1时,在x方向的平均囚禁范围大约3mm,在z方向4mm(如图中红点),而离子数为N2时在x方向的平均囚禁范围大约是1mm,在z方向是1mm(如图中蓝点)。假定y方向和x方向是对称的,那么前者的囚禁体积大约是后者的40倍,而粒子数前者是后者的100倍,因此前者的粒子数密度大约是后者的2.5倍。从图9(c)中也可以看到离子数为N1时离子平均速率大于1.5mm/μs(如图中红点),而离子数为N2时离子平均速率小于0.5mm/μs(如图中蓝点),因此离子的平均速率前者是后者的3倍以上。由以上分析可见这里模拟得到了和理论分析相同的结论。
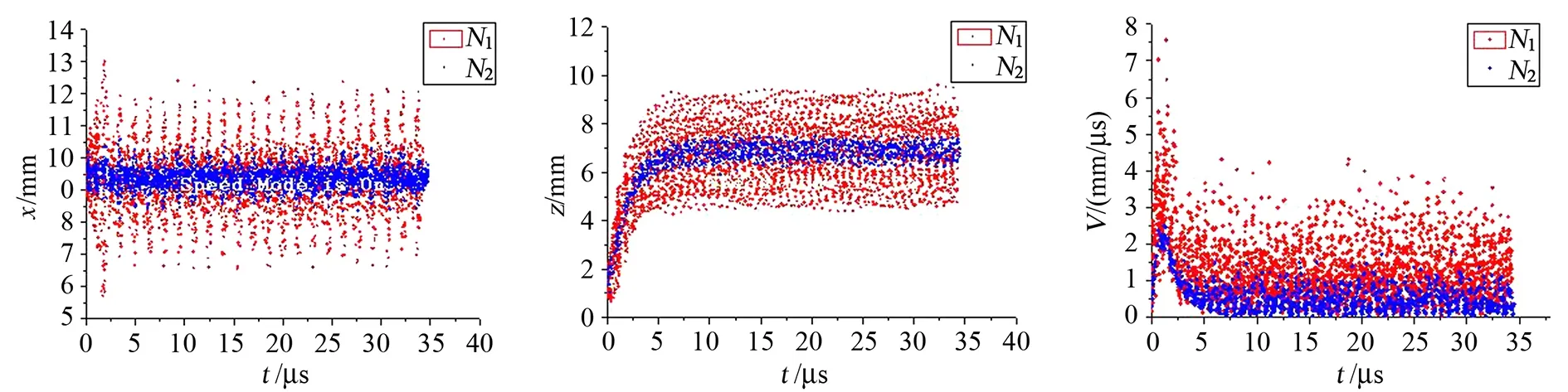
(a) x方向运动 (b) z方向运动 (c) 运动速率(a) Ion motion in x orientation (b) Ion motion in z orientation (c) Speed of ion motion图9 囚禁不同离子数目时离子的运动轨迹及速率变化Fig.9 Trajectory of ion motion and variation of its speed when the number of ions trapped is changing
由以上分析可知,囚禁的粒子数目不同时,阱中囚禁的离子密度也不同。除此之外,研究不同极数的离子阱内稳定囚禁时离子的分布及粒子数密度的不同也是一个重要问题。以下分别模拟了相同的阱结构参数及囚禁参数下四极阱和十六极阱中稳定囚禁时离子数密度的分布,分别考察了径向和轴向两个角度的粒子数密度分布特征,分别如图10和图11所示。模拟发现,四极阱中离子分布范围要比十六极阱中小很多,例如此时四极阱中离子径向分布范围的半径约为1mm,轴向宽度约为1.5mm,而十六极阱中离子径向分布范围的半径有3.5mm,轴向宽度有3mm。四极阱中离子分布在径向阱中心附近,且越靠近阱中心粒子数密度越大,而十六极阱中离子分布从径向阱中心几乎一直到杆电极的整个阱,且主要分布在径向的阱中间部位。 重要的是,四极阱中的粒子数密度要比十六极阱中粒子数密度大许多,尤其在径向方向,例如最大值处前者甚至可达后者的40倍,模拟结果和理论分析相一致。分析四极阱和十六极阱中粒子数密度分布出现如此差别的主要原因是两种离子阱中的势场分布不同引起的,例如比较四极阱,十六极阱中势场更加平坦,较低电场的范围更广等。

图10 四极阱和十六极阱中径向粒子数密度分布Fig.10 Radial ion density in separated ion trap
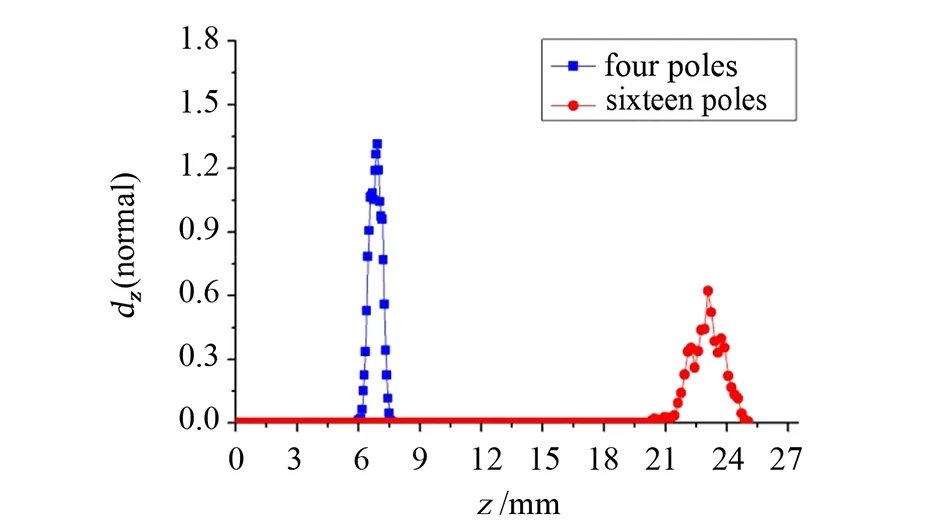
图11 四极阱和十六极阱中轴向粒子数密度分布Fig.11 Axial ion density in separated ion trap
4 离子囚禁、穿梭模拟
本节模拟研究了四极-十六极分区式离子阱中汞离子的囚禁、穿梭全过程。在分区式离子阱几何结构、尺寸及电气参数、囚禁条件优化的情况下,我们模拟了汞离子数目为2×106的离子云,初始在四极阱中产生,离子云初始在径向阱中心以半径为0.5mm的实心球分布,在四极阱和十六极阱内的囚禁时间分别设置为0.1ms,穿梭时间为10μs,离子云连续地周期性囚禁、穿梭。首先模拟了离子云在囚禁、穿梭过程中在x、y、z三个方向上的运动范围即离子云体积以及运动轨迹随时间的变化,模拟的总时长为1.2ms,约5个周期,如图12所示。图中黑线、红线和蓝线分别代表离子云在x、y、z方向上的运动轨迹。从图中看到,离子云能够被稳定囚禁、穿梭,且在十六极阱中离子云在三个运动方向上的运动范围都要比在四极阱中的大,在x、y方向均大约是四极阱中的3倍,在z方向约是四极阱中的2~3倍。单个周期内的离子云囚禁、穿梭过程如图13所示。从图中能更加详细地观察到,在四极阱中离子云达到稳态后在径向(即x和y方向)分布比较集中且离子密度分布较为均匀,而在十六极阱中径向离子密度分布并不均匀,离子集中分布在某些径向位置上,这和第2节中十六极阱中粒子数密度分布相吻合。穿梭过程中离子云从十六极阱穿梭到四极阱后很快能够达到稳态的分布平衡,而从四极阱穿梭到十六极阱后需要有一个弛豫到稳态重新分布的过程,这个过程大约需要10μm~20μs的时间。另外,在z方向离子云到达四极阱中有一个很短暂的弛豫时间才能达到稳态,这是由于端电极和穿梭时序造成的,并不能反映离子阱的物理特性。
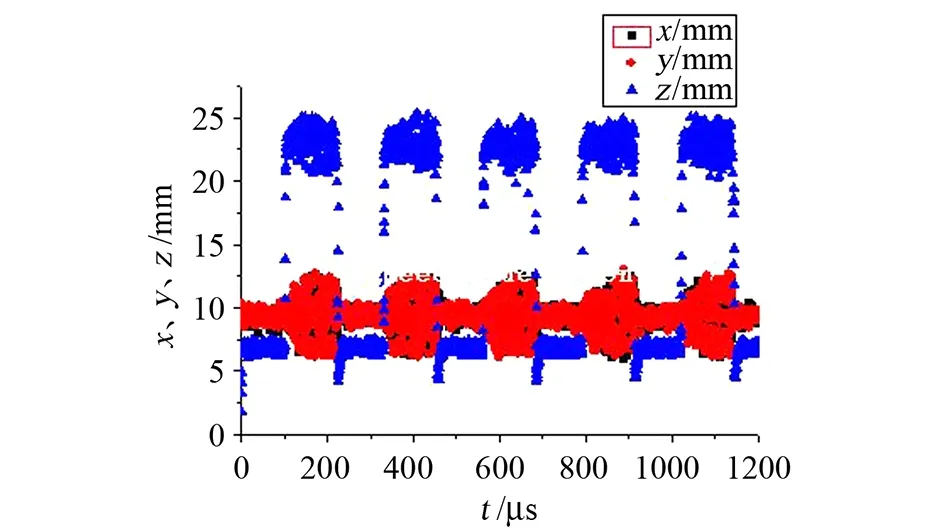
图12 分区式阱中离子云周期性囚禁、穿梭运动范围Fig.12 Movement range of ion clouds being trapped and shuttled in cycles

图13 分区式阱中离子云单周期囚禁、穿梭运动范围Fig.13 Movement range of ion clouds being trapped and shuttled over a period of time
在以上模拟过程中离子云在两阱之间穿梭过程也不相同,从四极阱穿梭到十六极阱时全部离子基本是同步穿梭,且穿梭所用时间也比较少,大约为2μs,如图14所示。然而离子云从十六极阱穿梭到四极阱时离子的穿梭有先后顺序,或者说是比较分散并不同步,每一个离子穿梭所用时间和四极阱穿梭到十六极阱时基本相同,但是由于全部离子的穿梭过程并不同步,所以全部离子都穿梭过去所用的时间就比较长,大约5μs,如图15所示。我们分析出现这种情况的原因是由于四极阱和十六极阱中势场不同,从而引起在两阱中稳定囚禁时离子的分布、在不同位置的离子所具有的电势能以及离子的速度和加速度等参数不同,最终造成离子云在不同方向的穿梭过程不同。
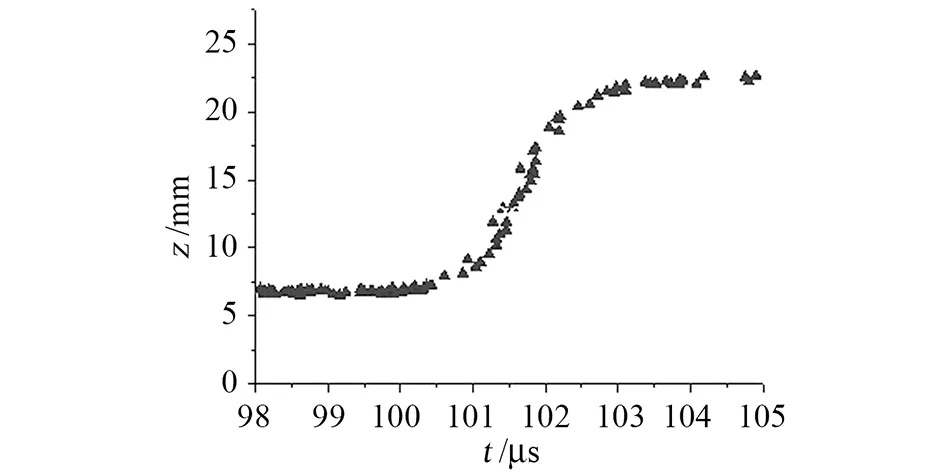
图14 离子云从四极阱到十六极阱穿梭过程Fig.14 Process of ion clouds shuttling from quadrupole trap to sixteen-pole trap

图15 离子云从十六极阱到四极阱穿梭过程Fig.15 Process of ion clouds shuttling from sixteen-pole trap to quadrupole trap

图16 不同囚禁区域离子云的运动速率Fig.16 Movement speed of ion clouds trapped in different trapping regions

图17 穿梭过程中离子云的运动速率Fig.17 Movement speed of ion clouds shuttling from quadrupole trap to sixteen-pole trap
在离子云穿梭过程中,除了研究其运动范围或者体积变化以外,更重要的是研究不同囚禁区域和穿梭过程中离子云的运动速度或速率的变化。基于设计建立的分区式离子阱系统模拟了汞离子云在其中囚禁、穿梭过程中的速率变化,模拟时间为0.7ms,大约三个周期,模拟过程中离子云始终为稳定囚禁,无粒子数衰减,如图16所示。从图中看到,在四极阱中离子云运动速率的分布范围比较大,大约是十六极阱中的2~3倍,平均速率也比较大,大约是十六极阱中的2倍,且速率比较大的粒子数密度分布比较低。离子云由四极阱向十六极阱中穿梭时的速率分布如图17所示。从图中可见,当离子云在两个势阱之间穿梭时,离子云的速率迅速增加至四极阱中囚禁速率的将近10倍(其中主要是z方向的速度分量),然后在端电极静电场的作用下离子云速率迅速减小,直至穿梭到十六极阱后达到稳态,整个穿梭过程大约需2μs,然而到达稳态则需约5μs。另外,在四极阱中还可以观察到离子云的速率随时间有周期性峰值出现,这与离子云周期性宏运动有关。
下面模拟研究了分区式离子阱中离子云周期性囚禁、穿梭过程中粒子数衰减。设置初始粒子数目Nr为1×105,总的囚禁、穿梭周期数St约90次,时长t约20ms,模拟的结果如图18所示。其中图18(a)中虚线为基本优化下粒子数随时间衰减情况,基本优化包括杆电极结构尺寸、稳定电压优化和缓冲气体参数优化,图18(a)中实线为完全优化后粒子数衰减情况,完全优化是在基本优化的基础上进一步优化端电极结构及电压、离子穿梭时间以及中间电极电压等因素。模拟研究发现基本优化下粒子数衰减非常快,离子云囚禁、穿梭20ms后粒子数衰减了近90%,而在完全优化条件下,粒子数衰减速率大大减小。其中优化了端电极结构及其电压之后离子云囚禁、穿梭将近90个周期(如图18(b)中虚线所示),约20ms后,总的粒子数衰减降低到50%,如图18(b)中实线所示。在此基础上,进一步优化离子穿梭时间及阱间电极电压,模拟发现在离子云囚禁、穿梭将近90个周期后仍能够被稳定囚禁的剩余粒子数可达95%,如图18(a)中红线所示。
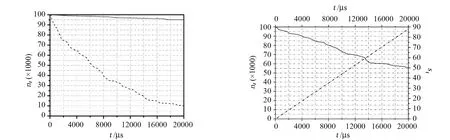
(a) 基本优化和完全优化下粒子数衰减 (b) 端电极优化下粒子数衰减 (a) Losing of ions after both basic optimization and full (b) Losing of ions after the electrode structure at both optimization have been accomplished ends has been optimized图18 离子数衰减 Fig.18 Decay of the ion number
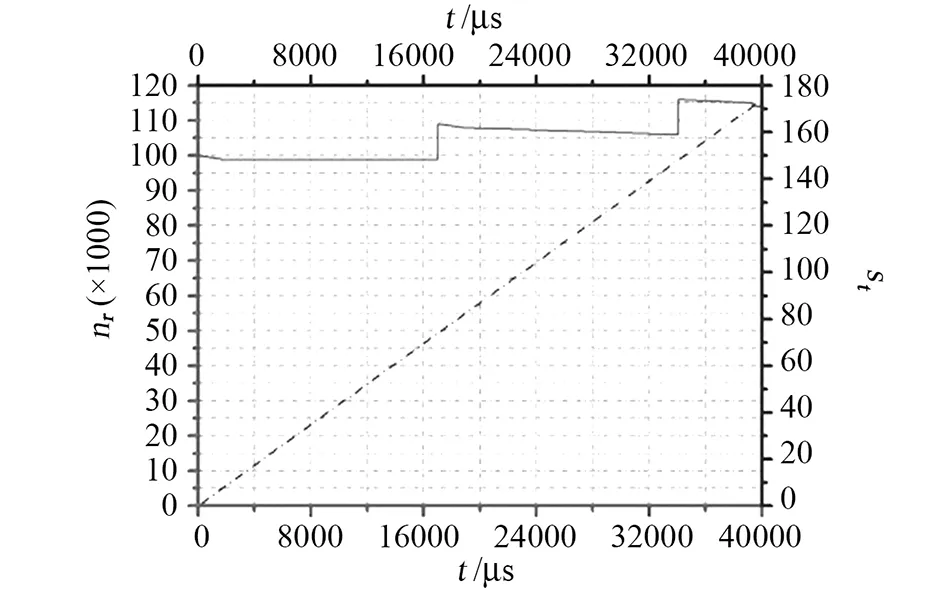
图19 完全优化下粒子数补充Fig.19 Ion compensation under the condition of full optimization
为了保持参与物理作用的粒子数有较高的信噪比和稳定性,进而减小粒子数涨落对微波钟频率稳定度的影响,本文模拟研究了粒子数周期性补充。设置初始粒子数目为1×105,离子囚禁、穿梭约80个周期(时间大约18ms)后进行一次粒子数补充,每次补充粒子数目为1×104,所补充粒子的初始条件包括粒子初始分布、粒子初始速度等均与首次产生粒子时相同。为了简单说明问题,在图19中仅模拟例证了囚禁、穿梭时间为40ms,大约170个周期时长的离子囚禁、穿梭和粒子数补偿情况。研究发现,为了保证信号强度稳定,粒子数涨落不宜过大,因此补充的粒子数要取合适值,例如本模拟中每次补充的粒子数为初始粒子数的2%~3%较为合适。
5 数据分析及讨论
模拟过程中,在十六极阱中杆电极所加的直流电压U0=0V,射频电压V0=100V,射频频率Ω=9.0MHz,离子阱中心到杆电极表面距离r0=5.2mm,汞离子质量m=199amu,带电量qe=1.602×10-19C,有公式(1)
(1)
可以得出十六极阱中离子囚禁稳定参量a、q值。将其带入离子在十六极阱中运动的宏运动频率公式(2)
(2)
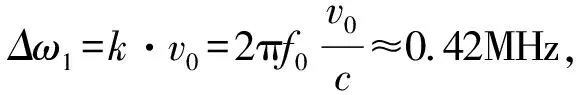
6 结束语
本文利用SIMION软件建立了分区式离子阱模型,模拟研究了离子阱不同囚禁区域中离子囚禁的一些基本问题,包括四极、十六极线型阱中的汞离子囚禁稳定区、离子运动特征、囚禁不同离子数目时的离子云速度以及不同极数的离子阱中各自的粒子数密度分布特征等。另外,进一步模拟研究了离子在分区式阱中周期性囚禁、穿梭过程中离子云的运动尺度、穿梭特性以及离子云的速度分布等在不同囚禁区域离子云所表现出来的不同特性,同时还模拟了优化条件下离子云多周期囚禁、穿梭过程中粒子数衰减和粒子数补充。最后,基于以上问题的模拟和研究,还估算了所建立的分区式离子阱中汞离子囚禁的多普勒效应和粒子数密度。
