基于灰色系统理论对城市年需水量预测的模型探究

郭 华，褚金鹏

(深圳市东深电子股份有限公司，广东 深圳 518057)

随着城市化进程的加快及水资源的相对短缺，对水资源进行合理管控和调度成为水资源管理部门关注的重点，需水量预测作为供水管理的前提和基础，在此阶段发挥出重要的作用。城市需水量预测的定量化和合理性能够为城市供水规划、经济发展和水资源的可持续利用提供基础的指导意义[1]。

国内外学者对需水量进行了大量的研究工作，并构建了多种不同的预测方法及模型，为后期需水量的预测方法的选取创建了条件。预测方法主要分为三大类，分别为时间序列法、结构分析法、系统方法。研究学者发现，每种模型的选取涉及的要素繁杂。为使建立的模型更加符合实际，本研究在考虑区域实际情况的基础上，选取灰色系统理论进行需水量预测。灰色预测模型将观测或统计得到的时间序列数据累加生成后再转化成微分方程，使模型更加规范及合理[2]。灰色预测模型以GM(1,1)模型作为预测模型，对城市的需水量预测具有较高的可靠性。

1 研究区概况

研究区属半湿润半干旱气候，全年平均气温在5℃～9℃，降雨量南多北少，年降雨量在300 mm左右，年平均蒸发量为1 250 mm，全区多年平均径流量9.493×108m3。区域常住人口数为6 301 350人，全区人均用水量为961 m3。本文以研究区在2005-2016年的《水资源公报》中的数据为依据，建立灰色模型，进而分析与预测未来城市年需水量。

2 城市年需水量灰色模型建模

2.1 模型建立的依据

将已知的信息看作白色系统，未知的信息看作黑色系统，将已知信息与未知信息看作一个系统，即为灰色系统[3]。对灰色系统的建模、预测、决策、优化等系列问题的理论成为灰色系统理论。将灰色系统用于预测城市年需水量，就是利用历年的城市年供水量为数据基础，建立城市年供水量与城市年需水量的微分方程，利用已知的数据计算未知年需水量[4]。将无明显关系的时间序列，通过建立相应的联系，变成有规律的时间序列。GM(1,1)被广泛用于科学研究中，为各种领域的发展起到积极的指引作用[5]。本文以研究区在2005-2016年历年城市供水量为基础数据，通过建立灰色模型，对城市需水量进行预测。

2.2 模型建立的方法

(1)

(2)

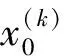
利用上述公式进行计算，结果见表1。

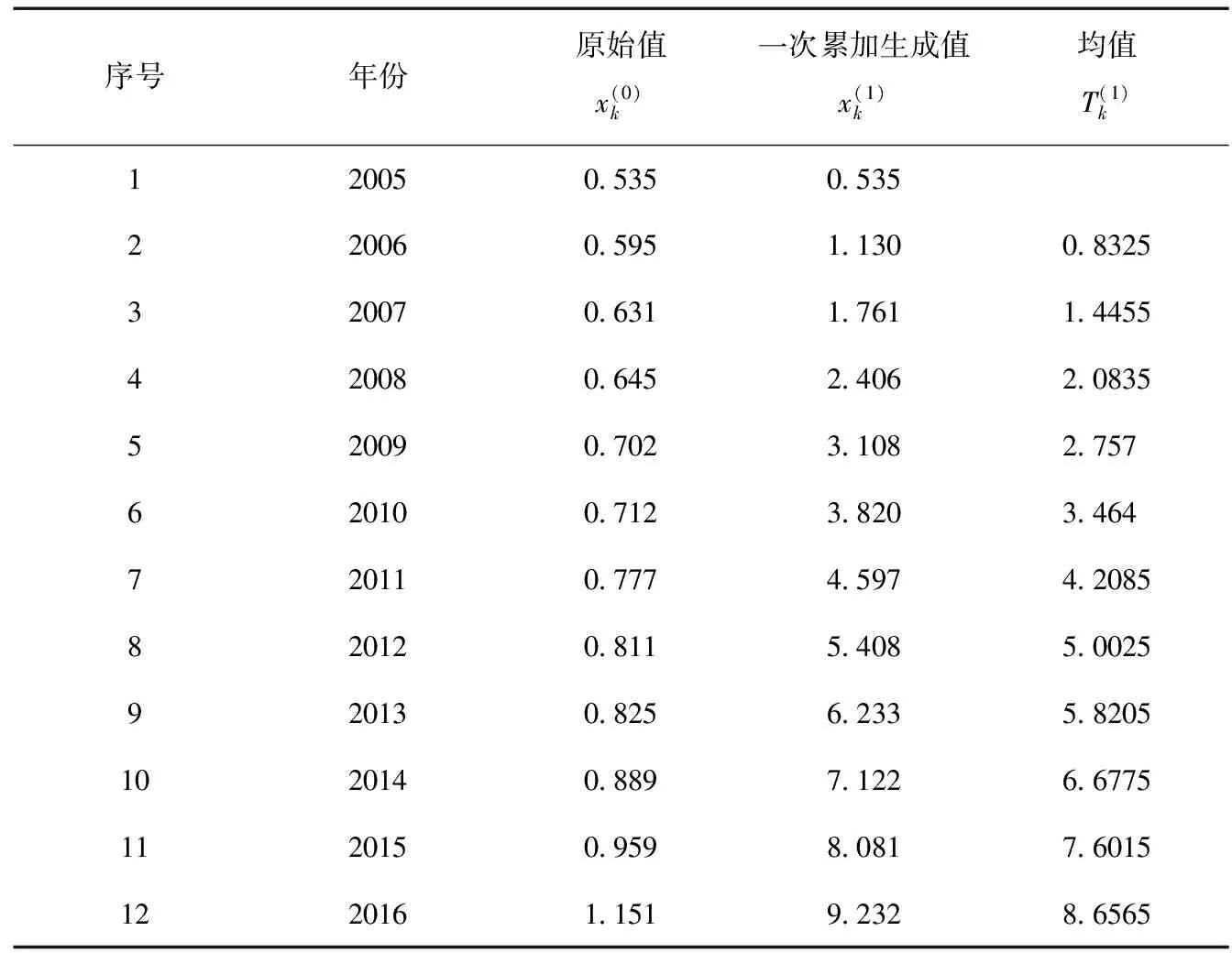
表1 研究区城市供水量、累加生成值及均值 /108m3

对累加生成的数列进行曲线拟合，函数表达式为：

(3)

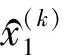
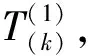
A=(BTB)-1BTY

则：

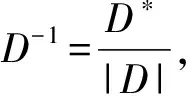
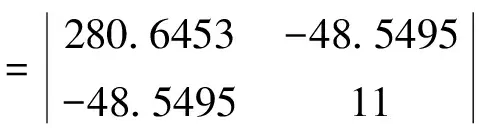
=730.04435

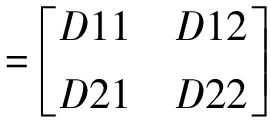
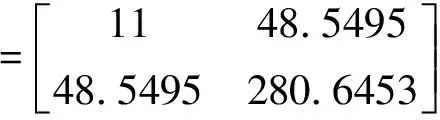
故

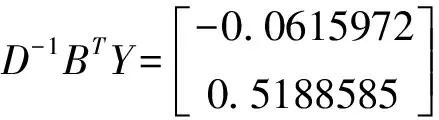
由上述计算可知：

a=-0.0615972

b=0.5188585

将a、b的值代入式(3)，计算得到需水量模型为：

则第k年的需水量为：

3 城市年需水量模型校核

为验证预测结果的准确性，根据灰色模型，计算研究区在2005-2016年的需水量，运用残差理论进行分析。将计算值与实际用水量进行比较，计算相对误差。公式如下：

(4)

(5)

式中：ε为残差值；η为相对误差。

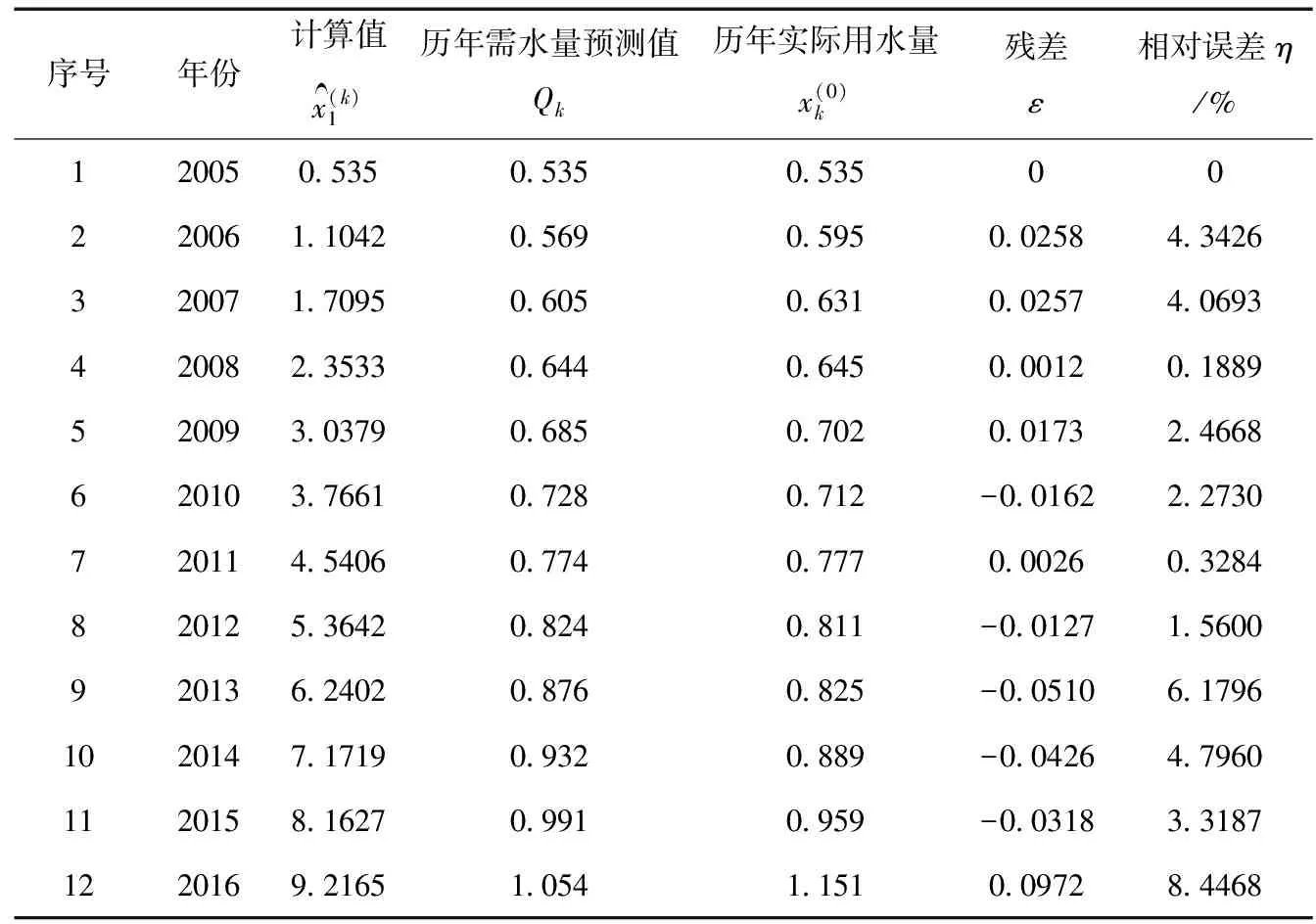
表2 城市需水量预测模型残差检验 /108 m3

由表2可知，城市年需水量模型的平均相对误差为3.16%，最大相对误差为8.446 8%，最小相对误差为0.188 9%，小于允许值20%。计算结果说明，模型可以用来预测研究区的年需水量，并且预测值相对较为准确。

4 灰色模型进行预测

根据建立的城市需水量模型，对研究区在2017-2030年的需水量进行预测，预测结果见图1。

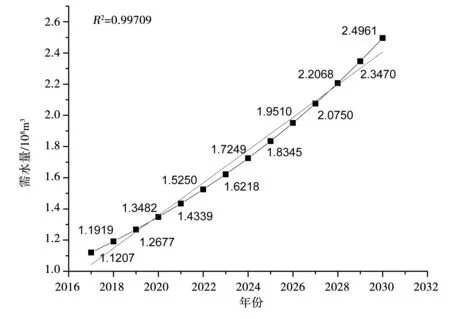
图1 研究区2017-2030年预测水量

通过对预测水量的图形进行分析发现,拟合曲线的系数超过0.99 ，说明对研究区需水量建立的模型是满足建模要求的。根据GM(1,1)适用于数列呈指数变化的情况，在历年水量变化形式上并非完全满足指数变化的前提条件下，还具有较高的可靠性，说明用GM(1,1)建模，预测城市需水量对城市后期的供水体系可以起到指导作用。

5 结 论

本文以研究区在2005-2016年的城市用水量为数据基础，运用灰色理论建立需水量模型，并利用残差理论分析计算数据的准确性，同时预测2017-2030年的城市用水量。此方法建立的模型较为准确，可将本文中的建模思想运用到实际的生产运行管理中，对水资源的评价、水量预测、水资源的合理利用具有重要的参考意义，可为后期水资源的调度提供数据支撑。