含纵向裂纹斜接弯管在内压作用下极限载荷的研究
2019-01-07王冉康志远漆向东徐浪苑鸿志
王冉,康志远,漆向东,徐浪,苑鸿志
(1.中国航天空气技术研究院,北京 100074;2.北京航天试验技术研究所,北京 100074)
0 引言
现代工业生产的高速发展使得压力管道趋向复杂化,操作运行条件更加苛刻,压力管道系统停用维修会带来严重的经济损失。而多种多样的压力管道缺陷表现为裂纹、未熔合、未焊透、气孔、夹渣等形式,其中裂纹对压力管道性能影响最为严重。
裂纹在一定条件下会造成压力管道失效,形式主要有:脆性断裂、韧性撕裂及塑性失效。其中,脆性断裂常发生在低温或材料性能严重裂化的情况下,会造成严重后果,但由于压力管道一般以钢铁材料制作而成,韧性较好,在发生脆性断裂前会先破坏塑性极限强度,因此纯粹的脆性断裂一般发生的可能性较小。
斜接弯管是一种较常见的压力管道非标元件,航天航空一些非标设备系统中可能会用到,且通常为现场焊制,而裂纹通常就集中在这种焊接接头部位(包括热影响区)。在用压力管道缺陷的安全评定技术因为其出故障时损失较严重而得到了极大的发展,但斜接弯管国内外研究相对较少。2007年J.Wood作过一篇有关安全评价技术的综述[1];大连理工大学应用数值方法分析过无缺陷斜接弯管的整体应力[2],及斜接弯管一些裂纹形式的线弹性计算[3-5]。本文主要分析含纵向裂纹斜接弯管的极限载荷。
无缺陷的低碳钢可视为理想弹塑性材料,计算极限承载能力可采用一定的简化力学模型。但缺陷极大的影响了材料及结构整体的应力应变场,含缺陷结构的极限载荷用力学理论模型难以精确的描述,而通过试验模拟要求条件较苛刻周期较长。所以本文采用3D有限元软件进行建模计算。
1 形状参数
斜接弯管为四节90°,壁厚为t,外直径为Do,公称直径为DN,管弯曲半径为R,直管段长度为L。裂纹形状简化为矩形(计算结果偏保守),如图1,裂纹深度为a,裂纹长度为b,裂纹位置为φ,φ=0°,90°,180°分别对应裂纹位于弯管的外弧线、中弧线和内弧线。用1个无量纲参数定义裂纹在弯管中的位置:a/t裂纹相对深度定义为α,用1个无量纲参数定义裂纹的几何形状特征:b/a裂纹相对形状定义为β。
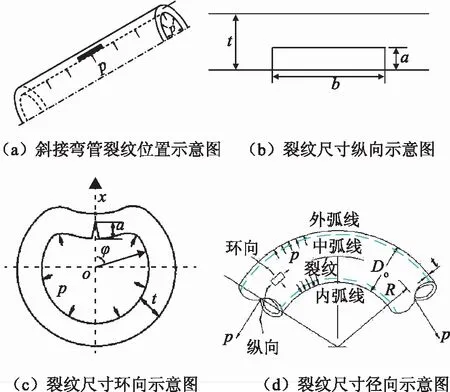
图1 斜接弯管裂纹尺寸及位置
R/DN=1.5,Do=377 mm,R=525 mm,L=500 mm,裂纹具体位置如图2所示。用1个无量纲参数定义斜接弯管的几何形状特征:Do/t管壁相对厚度定义为γ。斜接弯管的极限载荷为PL,弯管内压为Pi。
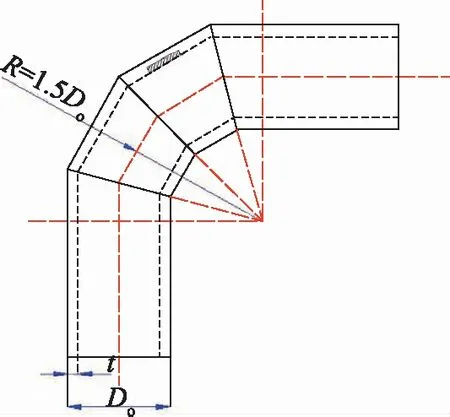
图2 斜接弯管及裂纹
2 建立模型
在3D有限元软件ANSYS中建立斜接弯管及裂纹的模型,如图3所示。在裂纹尖端选用了与斜接弯管实体不同的三维单元退化等参奇异元Solid95,并加密了尖端及附近的网格,以更加精确的模拟裂纹尖端极度变化的应力应变场。斜接弯管材料取普通碳钢材料,对弯管内壁面施加载荷内压,两端进行全约束。通过ANYSY自带语言完成编程、建模和计算。
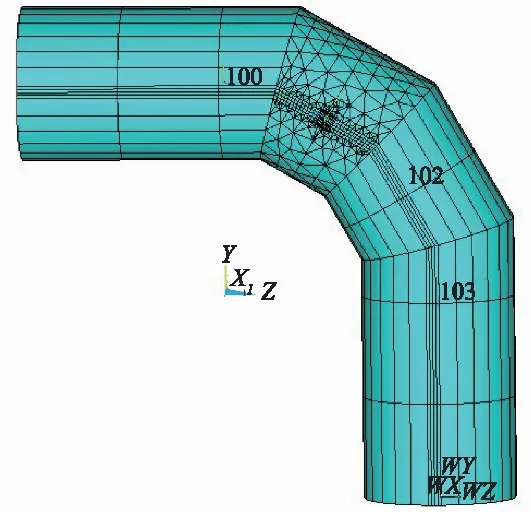
图3 斜接弯管及裂纹结构网格划分
3 结果分析
分别计算斜接弯管在半穿透纵向裂纹和穿透裂纹在内压作用及不同几何参数下的极限载荷,然后分析各几何形状参数α,β和γ对含裂纹结构极限载荷的影响。
3.1 斜接弯管含半穿透纵向裂纹
3.1.1形状参数α对极限载荷的影响
取裂纹位置角度φ为90°,固定裂纹相对长度β,分析结构的极限载荷PL随裂纹相对深度α的变化规律,变化固定值β可以得到PL-α曲线族。Pi=50 MPa,Do/t=18时,PL-α曲线族如图4(a)所示;Pi=100 MPa,Do/t=12时,PL-α曲线族的变化规律如图4(b)所示。
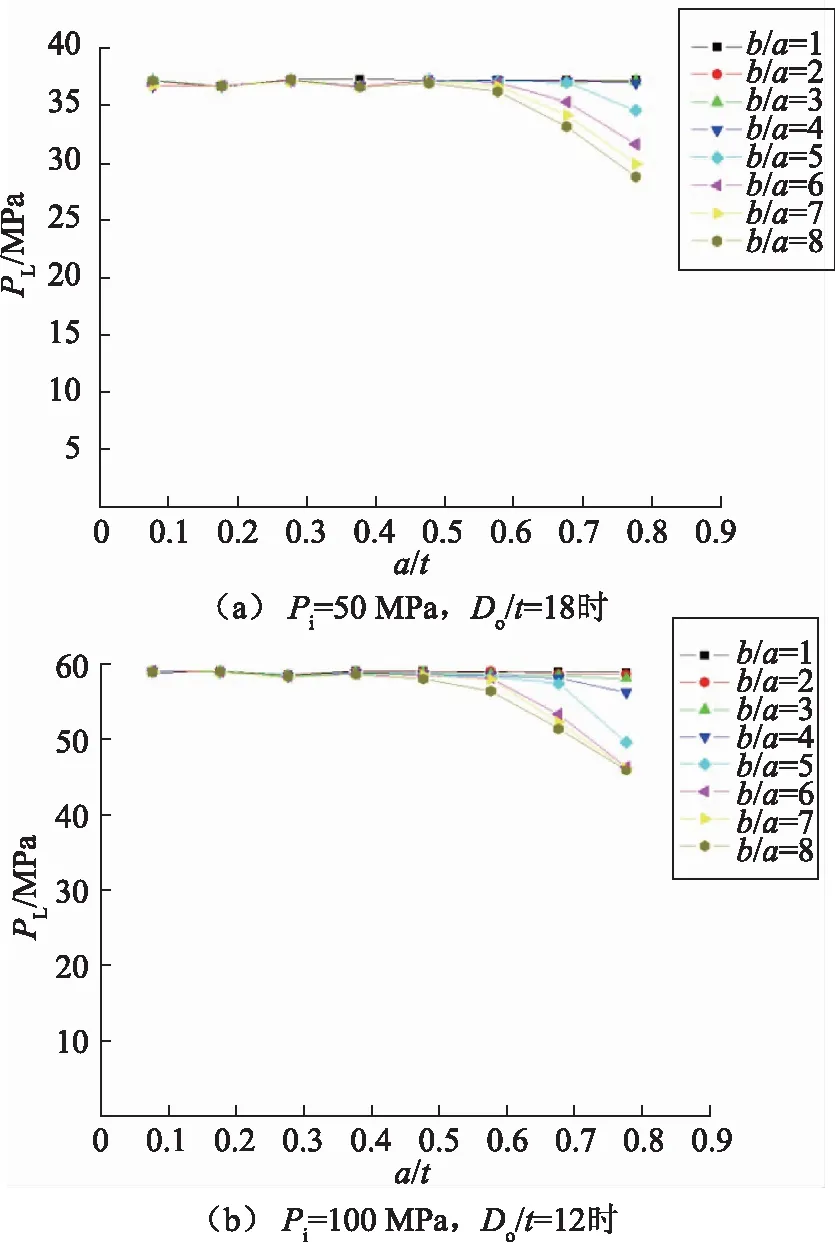
图4 极限载荷-相对深度(PL-α)曲线族
观察曲线族可以发现,内压作用下斜接弯管的极限载荷PL随形状参数α的变化有两种情况。开始随着α的变大,结构的极限载荷PL无明显波动,基本保持不变;随着α逐渐增大至一定值(α=0.4~0.5),极限载荷曲线PL-α由平直的直线开始下降,下降趋势近似线性。我们将曲线的拐点定义为结构极限载荷下降的临界形状参数α0。这个临界值α0随裂纹相对长度β而变,α0-β变化曲线也存在一段直线区。开始时β变大,临界值α0基本保持不变;但当β增大至一定值(0.4左右)后,临界值α0开始变小,结构更早出现极限载荷PL下降的情况。
3.1.2形状参数β对极限载荷的影响
取裂纹位置角度φ为90°,固定裂纹相对深度α,分析结构的极限载荷PL随裂纹相对长度β的变化规律,变化固定值α可以得到PL-β曲线族。Pi=50 MPa,Do/t=20时,PL-β曲线族如图5(a)所示;Pi=50 MPa,Do/t=16时,PL-β曲线族如图5(b)所示。
观察曲线族可以发现,内压作用下斜接弯管的极限载荷PL随形状参数β的变化也有不同情况。当α比较小的时候(α≤0.5),PL-β曲线基本成直线,随着β的增大,PL保持基本不变;α增大至一定值(α>0.5)后,PL-β曲线的变化规律与PL-α曲线类似,开始随着β的变大,结构的极限载荷PL无明显波动,基本保持不变;β逐渐增大至一定值后(β=3~5),极限载荷曲线PL开始下降,下降趋势也成基本线性。同样也存在极限载荷曲线的拐点和引起结构极限载荷下降的临界形状参数β0。这个临界值β0也随裂纹相对深度α而变化。β0-α变化规律与α0-β类似,刚开始随着α的变大,临界值β0基本保持不变;但当α增大至一定值(0.5左右)后,临界值β0开始变小,结构更早的开始出现极限载荷PL下降趋势。β0-α的变化更剧烈。
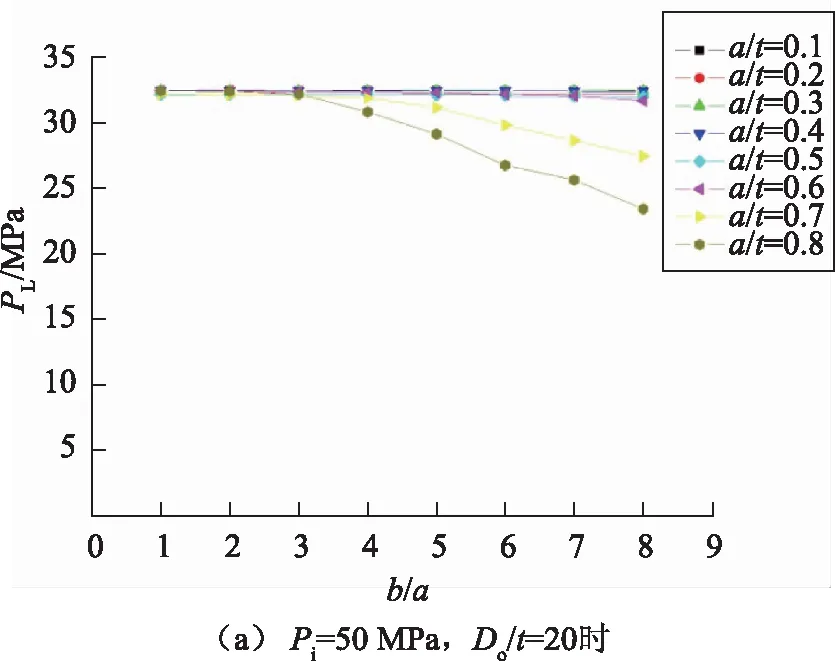
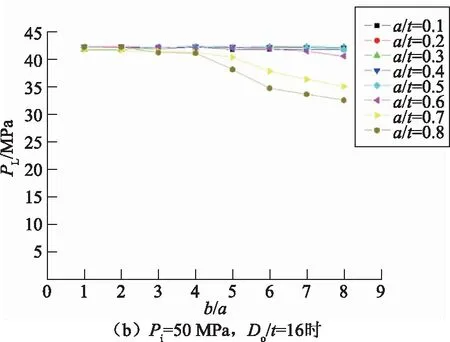
图5 极限载荷-相对长度(PL-β)曲线族
3.1.3形状参数γ对极限载荷PL的影响
取裂纹位置角度φ为90°,固定裂纹相对深度α,固定裂纹相对长度β,分析结构的极限载荷PL随形状参数管壁相对厚度γ的变化规律。Pi=100 MPa时,PL-γ在不同的裂纹相对深度α和相对长度β下的变化曲线如图6所示。
可以看到,结构的极限载荷PL随γ的增大成非线性的减小,且极限载荷PL的下降梯度逐渐变小,表示结构的削弱趋势稍放缓;其他形状参数α和β的变化对PL-γ变化趋势没有很明显的影响。
Pi=100 MPa,β=6时,变化α得到PL-γ曲线族如图7所示;Pi=100 MPa,α=0.7时,变化β得到PL-γ曲线族如图8所示。
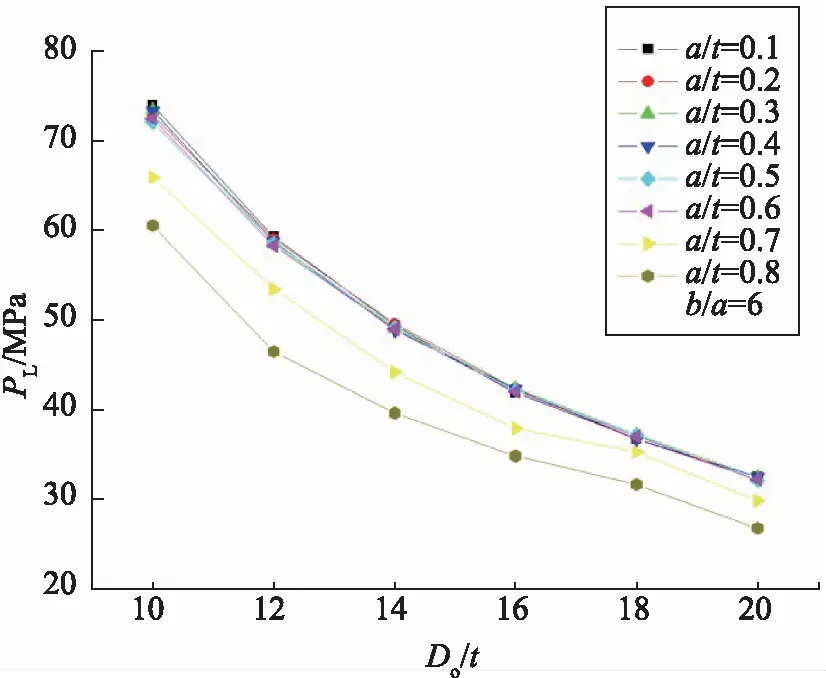
图7 Pi=100 MPa,β=6时,PL-γ(Do/t)曲线族
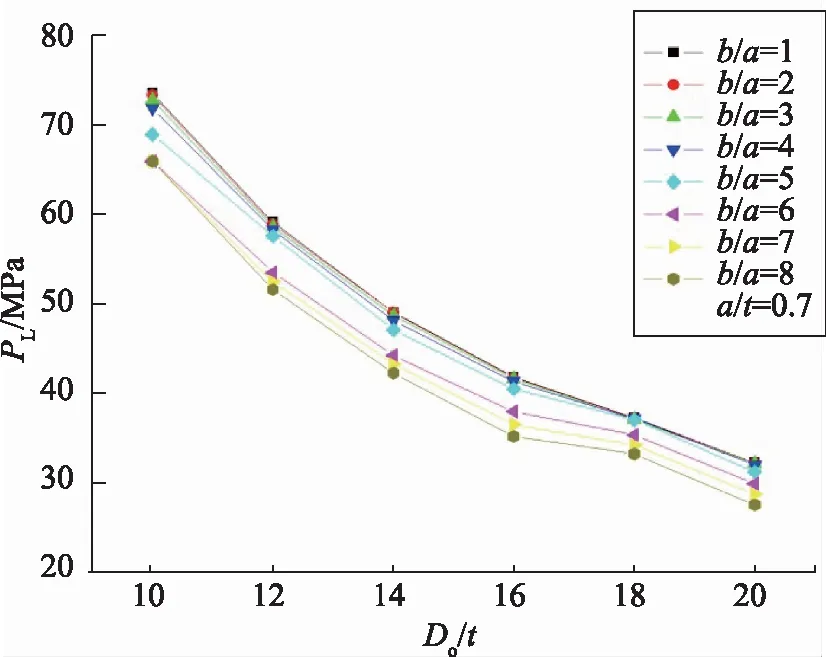
图8 Pi=100MPa,α=0.7时,PL-γ(Do/t)曲线族
3.2 斜接弯管含穿透裂纹
斜接弯管穿透裂纹的3D有限元模型需重新建立,如图9所示。模型建立方法与半穿透裂纹类似。对于穿透裂纹,形状参数α=1(a=t),β=b/t。
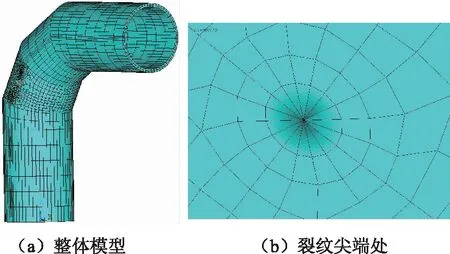
图9 穿透裂纹的3D有限元模型
取裂纹位置角度φ=90°,Pi=100 MPa时,变化管壁相对厚度γ得到PL-β曲线族如图10所示。
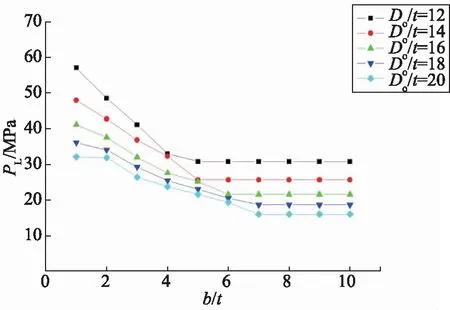
图10 Pi=100 MPa时,PL-β曲线族
穿透裂纹较明显的削弱了结构的极限承载能力,相比半穿透裂纹极限载荷变化曲线不存在开始的直线段区。在β很小时,PL就开始明显的下降,下降趋势基本成线性,且γ越大,PL的下降梯度越大,说明穿透裂纹对厚壁结构极限载荷有更大的削弱作用。β增大到一定程度会超过结构单节最大长度达到最大值,极限载荷PL也就不会再发生变化。
Pi=100 MPa,变化β得到极限载荷PL-γ曲线族,如图11所示。随γ的增大,结构极限载荷呈下降趋势,但PL的下降梯度也在减小,说明穿透裂纹对结构极限载荷的影响在随管壁的减薄而减弱。
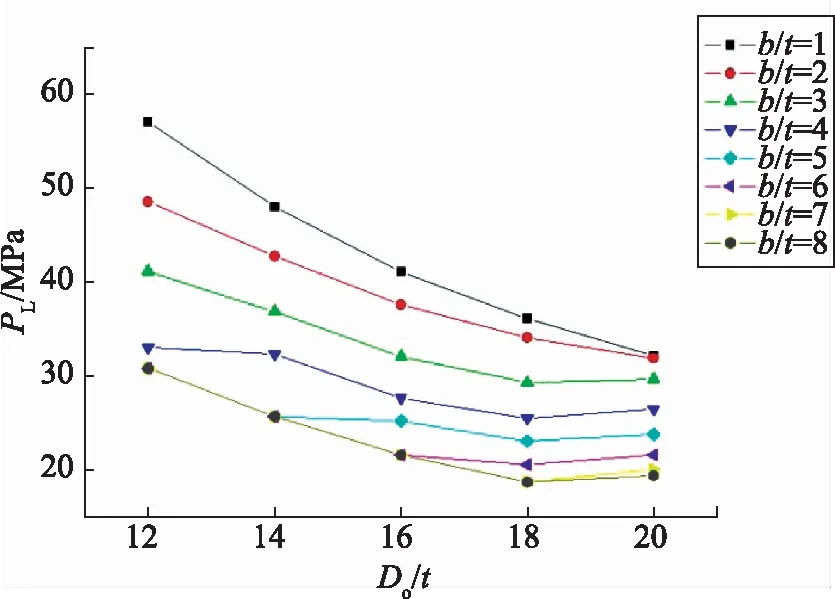
图11 Pi=100 MPa时PL-γ(Do/t)曲线族
4 结论
纯内压下纵向裂纹对结构极限载荷PL的影响可总结为:①半穿透裂纹只有深度长度大到一定值才会对结构极限载荷造成明显的削弱,PL-α,PL-β变化曲线开始都存在直线区,PL随α,β的增大基本不减小,当α,β增大到一定临界值α0,β0时,PL才开始比较明显的下降;②结构极限载荷PL对形状参数α的变化更为敏感,α对PL的影响要大于β;③随形状参数γ的增大,极限载荷PL逐渐减小,但PL变化梯度也在变小,薄壁管的极限载荷受裂纹影响更小;④穿透裂纹极大的削弱了斜接弯管的极限承载能力,PL-β变化曲线不存在半穿透裂纹中出现的直线区。
