利用RBF实现线状工程中GNSS高程转换的精度分析
2019-01-07陈智伟张兴福
陈智伟,张兴福,胡 波,刘 成
(1.广东工业大学测绘工程系,广东 广州 510006;2.中国铁路设计集团有限公司,天津 300251)
GNSS测量能够精确快速获取地面点的三维坐标,通过坐标转换可以获得地面点在国家或工程坐标系中的高精度平面坐标,但是由于GNSS测量获取的是大地高,无法直接用于工程建设,需要通过高程转换将大地高转换为正常高。高程转换的精度受数学模型、GNSS/水准点的密度,以及分布情况、测区高程异常起伏大小等多重因素的影响,因此在实际应用中还需要开展大量的试验研究。
目前确定高程异常值的常用方法主要有:函数模型拟合法[1-4](平面、曲面等)、区域似大地水准面模型法[5-6]、重力场模型法[7-9]、基于移去恢复技术的函数模型拟合法[10-12]等。不同方法具有不同的适用性,其高程转换的精度也各不相同。径向基函数(radial basis functions,RBF)以其结构简单、拟合精度较高、收敛速度快等优势被广泛应用于非线性函数逼近、模型分类等领域[13]。因此本文以美国GSVS2011项目的GNSS/水准数据为例,对利用RBF实现GNSS高程转换方法展开研究,详细分析Thinplate、Cubic、Gaussian、Multiquadrics、Linear 5种RBF核函数的GNSS高程转换精度。
1 方法和原理
RBF可以看作是一个高维空间中的模型拟合(逼近)问题,通过学习在多维空间中寻找一个与训练数据最佳匹配的模型,用该模型处理检核数据。RBF的结构分为3层:第1层为输入层,将已知数据通过该层输入系统,作为训练学习的基础;第2层为隐含层(核函数层),作为已知数据训练的依据;第3层为输出层,通过对核函数训练模型的结果进行加权处理[14-15],使输出结果达到最优。数据处理基本流程如图1所示。

图1 数据处理流程
下面为5种RBF核函数的表达式,用φ(r)表示。
Thinplate核函数
φ(r)=r2ln(r+1)
(1)
Cubic核函数
φ(r)=r3
(2)
Gaussian核函数
(3)
Multiquadrics核函数
(4)
Linear核函数
φ(r)=r
(5)
径向基函数的插值函数表达式为
(6)
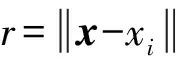
2 算例及精度分析
本文采用美国GSVS2011项目(https:∥www.ngs.noaa.gov/)的GNSS/水准数据,该线路长度约325 km,共有218个GNSS/水准点,相邻两个点相隔约1.5 km,线路GNSS/水准点分布和沿线高程异常起伏情况如图2、图3所示。利用该数据对第1节中5种RBF核函数的拟合精度进行分析,本次试验共有6种选点方案,具体方案见表1。表1中“a(5 km)”代表方案a中的点间距约5 km,其他以此类推。为了方便论述,用字母T、C、G、M、L分别代表Thinplate核函数、Cubic核函数、Gaussian核函数、Multiquadrics核函数、Linear核函数。

图2 GNSS/水准点分布情况

图3 沿线高程异常起伏情况

表1 选点方案
根据以上6种选点方案分别进行数据处理,采用式(7)进行精度统计
(7)
式中,vi为检核点的实测值和拟合值的差值;n为检核点的个数。
RBF的5种核函数在各检核点处的残差值如图4所示,残差值的最大值、最小值、平均值与拟合精度统计结果见表2。各模型在不同点间距情况下的高程拟合精度如图5所示。
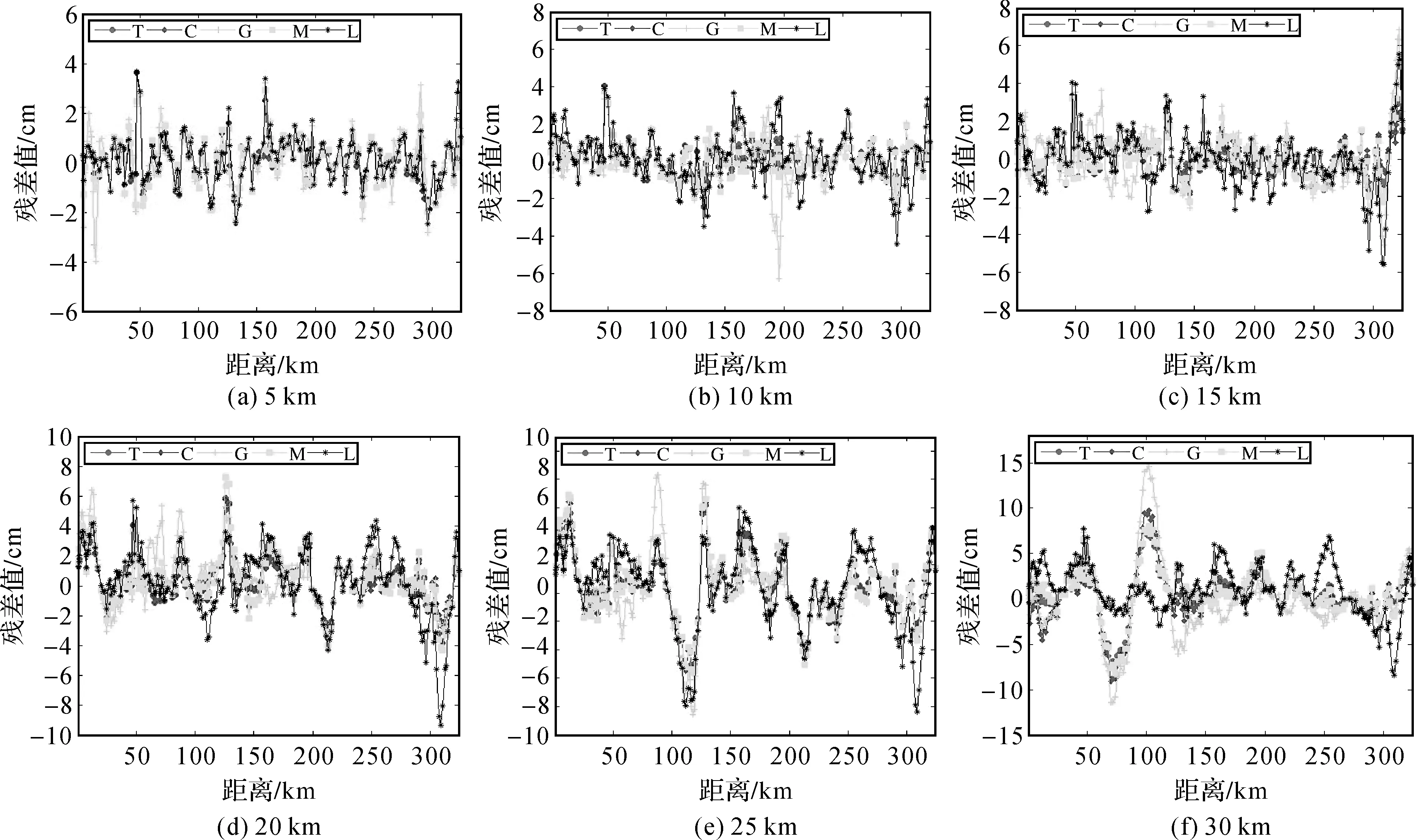
图4 各方案残差值

表2 拟合高程精度统计 mm
由表2及图5可知,除核函数G外,其余核函数高程拟合残差绝对值均不超过10.0 cm;当点间距不大于15 km时,T、C、M这3种核函数的拟合精度相当,拟合精度约1.0 cm,高程残差绝对值均小于5.0 cm;当点间距从15 km减小到5 km时,G、L两种核函数拟合精度分别从1.7 cm、1.6 cm提高到1.2 cm、1.0 cm,而且点间距为5 km时,高程拟合残差绝对值均不超过4.0 cm;当点间距30 km减小到15 km时,5种核函数的拟合精度迅速提高,分别提高了1.6 cm、2.1 cm、2.5 cm、1.7 cm和1.3 cm,而且点间距为15 km时,高程拟合残差绝对值均不超过7.0 cm。
为了进一步分析5种RBF核函数的拟合精度,现根据工程测量规范(GB 50026—2007)对6种方案的高差拟合精度进行统计,统计结果见表3。由表4可知,T、C、M这3种核函数在各种选点方案中超过95.3%的拟合高差均满足四等水准测量的限差要求,而且在方案b中能达到98.0%;G、L两种核函数分别有超过90.7%和92.5%的拟合高差满足四等水准测量限差要求。高差拟合精度超出四等水准测量限差的测段主要出现在线路约50 km、85 km、200 km和300 km等处(如图3所示),原因是这些区域的高程异常变化复杂,在50 km处的高程异常变化尤为明显。另外,除了方案a中的核函数G满足五等水准测量限差要求的比例为95.4%,其他的方案满足五等水准测量限差要求的比例均超过98%,而且超限的测段主要在线路约50 km处。

图5 高程拟合精度统计

表3 拟合高差精度统计 (%)
3 结 论
本文研究基于5种RBF核函数的高程拟合方法,统计分析了不同点间距下各种核函数模型在拟合线状工程中GNSS高程转换的精度,结论如下:
(1) 高程拟合精度统计表明,当点间距较小时,5种核函数均能获得较好的拟合精度。当点间距从30 km减小到15 km时,5种核函数的拟合精度均迅速提高;当点间距不大于15 km时,T、C、M这3种核函数的拟合精度约为1.0 cm。
(2) 在高差精度统计中,T、C、M这3种核函数满足四等水准测量限差要求的比例超过95.3%,满足五等水准测量限差要求的比例超过98.0%,均优于G、L两种核函数。
(3) 在高程异常变化较为平坦的测区,用RBF拟合时建议点间距不宜大于30 km。
