变刚度连续型机械臂设计与控制
2019-01-07耿仕能王友渔陈丽莎康荣杰
耿仕能,王友渔,陈丽莎,王 聪,康荣杰
(1. 天津大学机构理论与装备设计教育部重点实验室,天津 300350;2. 北京空间飞行器总体设计部,北京 100086; 3. 天津工业大学机械工程学院,天津300387)
0 引 言
建立稳定的空间在轨服务系统是太空资源开发的重要手段。通过研制先进空间机械臂完成面向合作或非合作目标的各类操作任务已经成为空间自主在轨服务技术的重难点[1]。在对非合作目标进行操作时,由于目标的不可控性,难免会发生接触碰撞或者意外干涉产生冲击,解决这一问题的办法是根据操作步骤和外部环境调节机械臂刚度来协调安全性与操作精度的平衡关系[2]。
目前,传统的刚性机械臂主要是依靠主动控制调节整体刚度,包括力位混合控制和阻抗控制。Paul[3]和Craig[4]等人提出的力位混合控制器可将末端执行器上任意方向的力和位置通过雅克比矩阵映射到各个关节控制器上。Zhang[5]等人运用等效的关节位置环代替操作空间的位置环对力位混合控制进行改进,一定程度上降低了控制计算量。阻抗控制是将未知的环境等效为一个阻抗模型,将力控制转换为位置控制的方法。Hogan[6]等人首先提出阻抗控制的概念,Salibury[7]等基于阻抗控制提出机械臂刚度的主动控制方法。虽然这两种主动柔顺控制方法可以调节机械臂末端或关节处的刚度,但对系统实时性计算能力要求高,参数寻优过程非常复杂,并且很难保证机械臂在所有方向和部位都具有良好的柔顺性,具有一定局限性。
为更好解决接触碰撞引起机器人运动和受力突变的问题[8],另一种思路是将具有被动柔性的连续型机械臂应用于可能产生碰撞的空间任务操作中。连续型机械臂是具有类似于章鱼触须柔性结构的新型仿生机械臂[9],在操作碰撞或意外干涉发生时,可依靠其本身的被动柔顺性来保证接触的安全性,而且对碰撞的方向、强度适应性更强。但进行操作时,过高的柔性却会削弱其承载能力与操作精度。通过有效的物理变刚度方法和闭环运动控制算法可以较好的解决这一矛盾,改善其操作性能。
目前连续型机械臂的物理变刚度方法主要可以分为两种,一种是通过丝驱动增加模块之间的内摩擦力,另一种是将连续型机械臂与Jamming机构相组合。麻省理工学院Chen[10]等人提出了一种由球形关节嵌合串联而成的可变刚度连续型导管,通过丝驱动改变球形关节之间的摩擦力提高整体刚度保持导管目标形状。卡耐基梅隆大学的Degani[11]等人设计了一种可按指定路径缓慢推进的连续型内窥镜,变刚度驱动丝可提高模块间球铰链的摩擦力来改变整体刚度。丝驱动变刚方法的原理与实现相对简单,但变刚度作用力容易对机械臂构型造成影响。Jamming阻塞机构是一种通过改变粒状介质之间的摩擦力来使物体在类流体状和类固体状态之间发生可逆转换的机构。Cheng[12]等将阻塞机构与线绳驱动的连续型机器人相结合起来,阻塞机构被密封在机械臂内部,通过控制气压来控制机械臂的整体刚度。为了克服传统阻塞机构体积庞大的缺点,Kim[13]等人设计了一种鳞状阻塞机构包覆于机械臂外层,留出了机械臂的内部通道。阻塞机构具有更好的变刚度效果,但是大量固体颗粒改变了机械臂的弹性特征,另外真空泵等额外装置的加入,使系统复杂化。
目前连续型机器人的运动控制主要是基于逆模型的开环控制。Walker[14]等采用模块等曲率弯曲假设来分析连续型机械臂的运动学特征,简化描述连续型机械臂的运动规律。由于假设存在误差以及构型容易受外力影响的原因,简化模型控制精度不佳。Rucker[15]等人建立了连续型机械臂的一般动力学模型,但是模型非常复杂,难以求出解析解。Baek[16]和Rone[17]分别用有限等曲率微元段来描述二维和三维的连续型机械臂形状,用有限参量表达构型,但仍然需要求解大规模非线性方程组,无法运用于实时控制当中。目前连续型机器人的精确控制与复杂模型之间的矛盾还未得到较好解决。
综上,在容易发生碰撞接触的空间操作任务中,连续型机械臂相对于刚性机械臂具有更好的适应性和安全性,但需要增加有效的物理变刚度方法和运动控制策略,才能弥补结构柔性所导致负载能力和操作精度不足的缺点。本文以提升连续型机械臂的操作能力,平衡操作安全性与操作精度的关系为目的,提出了一种适用于丝驱动连续型机械臂的变刚度机构,并对变刚度控制策略进行初步研究,同时提出一种基于末端位置传感器位置反馈的闭环控制器。本文着重研究可用于空间操作的连续型机械臂在物理变刚度及闭环控制方面的基本理论和实现方法,并设计搭建了样机平台进行验证。对于实际投入空间操作的机械臂,还需进一步考虑高真空、大温差,强辐射等环境特点以及操作目标的质量、体积、自旋及章动等物理特征进行工程化设计。本文第1部分阐述了机械臂及其驱动装置的结构设计和变刚度机构的原理及设计;第2部分运用单关节等曲率模型对机械臂进行运动学分析;第3部分给出基于运动学模型的机械臂末端轨迹的闭环运动控制方法及变刚度控制策略;最后,在第4部分进行了运动控制和变刚度控制的实验验证。
1 可变刚度连续型机械臂的设计
本文所提出的可变刚度连续型机械臂样机如图1所示,由可变刚度连续型机械臂本体、末端执行器、驱动箱和电器柜组成。连续型机械臂总长度为960 mm,外径为38 mm。其表面覆盖了一层尼龙编织网套。末端执行器和连续型机械臂之间具有标准互换性接口,可根据任务需求更换不同的末端执行器,图中为一个三爪夹持器,由直线步进电机驱动,中央安装有一个微型摄像头。以下将分别介绍各部分的具体结构。
1.1 机械臂本体设计
以超弹镍钛合金作为中央脊椎丝和驱动丝,机械臂采用脊椎式结构设计。如图2所示,连续型机械臂一共包括两个连续型模块,本文中称连续型关节。靠近驱动箱的关节定义为关节1,末端关节定义为关节2,每个关节长度为480 mm。每个连续型关节由连接盘、中央脊椎丝和圆周120°间隔均匀分布固定在对应关节末端盘的三根驱动丝组成,其中关节2的驱动丝穿过关节1与驱动箱连接,关节2的驱动丝与关节1驱动丝之间相错60°。中央脊椎丝和所有驱动丝的材料都为超弹镍钛合金,具有非常好的弹性和强度,保证了连续型机械臂本体的柔顺性和可靠性。另外,这种硬质弹性丝能承受推力的性质使得它的驱动效率和驱动精度更高。所有连接盘在中央脊椎丝上等距分布并与中央脊椎丝固联,驱动丝与对应关节末端连接盘固联,但是与关节内其它连接盘没有固联,可以发生相对滑动。因为中央脊椎丝长度不可改变,以不同长度组合推拉各驱动丝时,中央脊椎丝和所有驱动丝在各连接盘的约束下发生弯曲变形,即实现了运动。对于不同的驱动丝长度组合,连续型机械臂都有一个唯一的构型与之对应。
1.2 驱动箱设计
驱动箱包含了用来驱动连续型关节驱动丝的所有部件。驱动丝推或拉的直线运动通过丝杆滑块传动机构来实现。如图3所示,一组丝杆、滑块、导轨组成一个传动模块。根据连续型机械臂驱动丝数量,驱动箱内一共包括六个周布的传动模块,各驱动丝与对应的传动模块的滑块固联。为检测驱动丝的驱动力,每个传动模块中在驱动丝的对称位置处布置了一个拉压力传感器,此另外拉压力传感器还可用来检测因环境因素(比如温差)引起的驱动丝应力变化,由此调整各驱动丝零位,补偿环境变化所致的应力、应变对系统的影响。图3所示为整个驱动箱可以分为两个部分,图中左半部分包含六组传动模块,右半部分用于布置电机和电机驱动器,电机和对应传动模块的滚珠丝杆通过联轴器连接。
1.3 变刚度机构设计
为改善连续型机械臂柔性结构负载能力和定位精度不够高的问题,引入变刚度设计。该连续型机械臂的变刚度机理是通过改变驱动丝与连接盘的摩擦力f控制它们之间相对运动实现的。如图4所示,如果能增加连接盘与驱动丝之间的接触压力N,从而提高所有接触点的摩擦力f来限制连接盘与驱动丝的相对运动,则可提高连续型关节整体抵抗变形的能力,即提高刚度。具体锁紧方法如图5所示,在每个连接盘上周向均匀分布铰接了三个带有橡胶帽的铜片。相邻连接盘上成对的铜片在温控记忆合金(SMA)弹簧收缩驱动作用下,橡胶帽会压紧驱动丝来限制驱动丝与连接盘之间相对运动。SMA弹簧在初始长度确定的条件下,其驱动力只与温度有关,SMA弹簧电阻一定时,温度与通路电流大小有关,因此只需设计电路控制SMA弹簧的通路电流I就能控制变刚度机构的锁紧压力N,从而控制连续型关节的刚度发生变化。
2 机械臂的运动学分析
2.1 驱动空间、构型空间与工作空间的映射关系
基于单关节等曲率平面弯曲的假设,每个不可伸缩的连续型关节具有两个自由度,即弯曲程度与弯曲方向[18],因此采用四个参数便能完全描述该双关节机械臂构型,具有四个自由度。为方便运动学分析,将连续型机械臂相关的运动学参数划分成三个空间,即反映驱动丝长度的驱动空间L=[l1,1l1,2l1,3l2,1l2,2l2,3]T,描述机械臂形状的构型空间Ψ=[θ1φ1θ2φ2]T,和描述末端绝对坐标值的工作空间Q= [xyz]T。其中驱动空间中li,k表示第i个关节的第k根驱动丝的总长度(i=1,2;k=1,2,3),驱动丝编号规则如图6所示。图7中,在与驱动箱固联的基盘和两个关节末端分别建立基坐标系{0}和两个局部坐标系{i}(i=1,2),其中θi为关节i在其主弯曲平面内的弯曲圆心角,主弯曲平面即弯曲圆弧所在平面;φi为主弯曲平面与该关节的基准坐标系{i-1}的x轴之间的转角。
根据实际样机设计,以上定义的构型参数取值范围为θi∈[0, π/2],φi∈[0, 2π]。另外已知各关节的中央脊椎丝的长度为lba,i=480 mm (i=1,2),以及对应驱动丝与{0}坐标系x0轴之间的夹角ωi,k,如图6中标注ω2,1=60°,周向驱动丝之间夹角相差为60°。
根据驱动丝与中央脊椎丝的几何关系可以得到驱动空间与构型空间的映射关系如式(1)所示,如图6,R为驱动丝的分布半径,R=15 mm。
(1)
基于坐标系的几何关系可以得到坐标系{i-1}到{i}的变换矩阵Ti(i=1, 2)如式(2),Rot表示旋转变换,Tr表示平移变换。
Rotz(-φi)
(2)
(3)
式(3)中T表示基座标系{0}到末端坐标系{2}之间的变换矩阵,其中P反映了末端点在基坐标系{0}中坐标值,即P=[PxPyPz]T反映了构型空间Ψ与工作空间Q的映射关系。
2.2 速度雅克比矩阵
雅克比矩阵揭示了工作空间、构型空间与驱动空间之间的速度关系,是对构型或末端位置点进行速度控制的基础。在该连续型机械臂当中,包括两个速度映射雅克比矩阵JΨL和JΨQ,分别表示构型空间Ψ到驱动空间L、构型空间Ψ到工作空间Q的速度映射。
构型空间到驱动空间的速度映射表示为式(4):
(4)
由式(1)可知L是构型空间Ψ各元素的多元函数所组成的向量,根据雅克比矩阵的定义求出对各变量的偏导数组成构型空间到驱动空间的雅克比矩阵如式(5)。
(5)
如式(6),所求得的构型空间到驱动空间的雅克比矩阵JΨL可分为四个2×3的分块矩阵,J1和J2分别代表关节1和2构型对本关节驱动丝速度的影响,由1.1节可知关节2驱动丝要穿过关节1,J21表达了关节1构型对关节2驱动丝速度的影响。
(6)
构型空间到工作空间的速度映射表示为式(7):
(7)
由式(2)(3)可知P是构型空间Ψ各元素的多元函数所组成的向量,P对各变量的偏导数组成构型空间到工作空间的雅克比矩阵如式(8):
(8)
为对末端轨迹进行控制,需要求出工作空间到构型空间的逆运动学关系。正如2.1节所述,该机械臂在构型空间具有的四自由度,分别对应Ψ的四个参数,因此相对于末端位置的三自由度(未考虑姿态)具有一个冗余自由度。对于冗余自由度机械臂其逆向速度关系如式(9)所示[19]:
(9)
(10)
3 运动控制策略与变刚度控制
如图8所示,控制系统由控制中心PC机和各类控制对象组成,控制对象包括六个直流有刷电机、数据采集卡、末端执行器的步进电机以及与PC直接连接的位置传感器(3D Guidance tranSTAR,测量精度0.5 mm)。数据采集卡模拟输入口用于实时采集各路拉压力传感器信号,模拟输出接入变刚度电路使得控制中心可直接控制机械臂刚度。在PC机VC++环境下,综合变刚度、运动控制策略和所有设备接口资源编写MFC控制窗口作为控制系统的交互中心。除位置传感器通过USB与PC直接连接外,控制通信系统是基于CAN总线建立。
3.1 闭环运动控制策略
由于2.1中所述的运动学模型是基于单关节等曲率假设建立的,本身存在一定误差,其次根据1.3可知连续型机械臂的构型容易受到外力影响,因此单纯运用逆运动学模型进行开环控制容易因产生较大位置偏差。通过在机械臂末端添加位置传感器,构建闭环控制算法可以不断消除误差而较好跟踪目标位置点[21]。
设运动过程中某时刻末端点误差为e,如式(11)它是目标位置Qd和实际位置Q的差值。
e=(Qd-Q)
(11)

(12)
根据现代控制理论[22],只要闭环系数矩阵Kp是正定的,则e趋近于零向量,系统稳定。一般选取对角矩阵作为Kp,理论上对角元素值越大,收敛速度越快,跟踪精度越高。
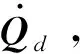
3.2 碰撞检测与变刚度控制
执行空间操作任务时,希望机械臂在接近并接触目标时具有较低的刚度,以降低碰撞冲击带来的损害;而接触完成后,希望机械臂具有较高的刚度,以保证一定的负载和定位能力。因此,在机械臂的变刚度控制中,首先需要检测碰撞发生的时刻以确定刚度切换的时机。本文提出一种利用驱动丝张力变化判断碰撞冲击的方法。如图10所示,当机械臂末端靠近操作目标发生横向或轴向碰撞时,产生接触力F,相应会引起机械臂固定端横向方向约束力偶Mo或轴向的约束力Fo的突然变化。在固定端对机械臂进行受力分析,可得到Mo是各驱动丝作用力Fi,k(i=1,2;k=1,2,3)简化到Oo点的主矩,Fo是Fi,k简化到Oo点的主矢,Mo和Fo与Fi,k满足如式(13)的关系,由于各驱动丝驱动力总是平行的,因此Fo始终在一条直线上,而Mo总处于与所有驱动丝垂直的平面内。
(13)

本文假设碰撞来源仅为待操作目标并且一次碰撞后即成功捕获目标,目的在于通过一种简化的控制策略证明机械臂物理变刚度的可行性。实际空间任务中碰撞来源及碰撞过程更为复杂,须采用更完善的传感器系统及控制算法实现碰撞检测。
4 运动控制与变刚度验证
4.1 运动控制验证
基准于图7的基座标系{0},在可达工作空间内规划1条如式(14)表达的空间螺旋轨迹,单位为mm。α表示末端点相对于x0轴绕O0转过的角度。运用3.1所示控制算法对机械臂进行运动控制,根据末端轨迹跟踪的误差分析,以验证本文基于运动学模型的闭环控制算法的正确性。
(14)
为了保证机械臂运动的平稳性,利用三角函数图像良好的平滑特性,规划α随时间的变化如式(15)的三角函数所示,使得各方向上的初始、终止速度以及加速度都为零,其中T为完成整个轨迹的总时间,T取为30 s。
(15)
图12(a)、(b)、(c)分别描述了x,y,z三个方向上机器人在开环控制和闭环控制(系数矩阵Kp=10I)条件下末端点跟踪上述目标轨迹的效果对比。实验结果显示只依靠逆运动学模型进行开环控制,单个方向上的位置误差最大会累积至30 mm,其原因是模型存在的偏差和连续型结构机械响应的迟滞带来的误差在运动过程中被不断积累。相比之下,闭环控制策略能将位置误差控制在2 mm内,因为位置反馈的加入,每个控制周期内出现的位置误差能够得到及时消除。
如图12(d)~(f)所示,如果在上述轨迹跟踪控制过程中在机械臂末端突加一个模拟由碰撞引起的较大位置误差,在x、y、z三个方向上的位置误差分别达到20 mm、15 mm、10 mm,但该闭环控制器可以克服外部干扰所带来的影响,经过3 s左右的时间即可使跟踪精度恢复到正常水平。通过以上两组实验验证可知该闭环控制器可以较好的克服由运动学模型和柔性变形带来误差,结合变刚度性能可很好的平衡安全性与操作精度的关系,提高机械臂的操作性能。
4.2 变刚度效果与控制验证
如图13(a)展示了本文所述变刚度方法调节改善机械臂整体刚度的效果。机械臂以竖直状态为初始状态,在1.3节所述变刚度机构中的SMA通路中施加不同大小的电流完成刚度调整后,在机械臂末端作用相同的横向载荷,如图所示试验载荷为1.5 N,发现不同电流作用下的变形效果不同。图13(a)中的系列形变中最右边的变形对应电流为0的情况,而最左边为初始未受力作用的初始形态,中间其他形态从右至左对应了电流逐渐增大的几种情形,反映了电流对刚度的影响。为定量分析SMA通路电流I对连续型关节刚度的影响,首先定义连续型机械臂刚度描述量。设在机械臂末端施加横向载荷F,测量不同电流下末端点的横向偏移量D,用载荷与偏移量的比值K描述该电流下的关节刚度。
按照以上刚度定义进行试验记录,得到如图13(b)机械臂刚度K随着SMA通路电流I的变化关系。当电流从0 A变化至2 A时,1.5 N负载下刚度由3 N·m-1变化至15 N·m-1。由此可知,对于该变刚度方法,控制通路电流I即能对机械臂整体刚度进行改善。后续工作将提高样机的加工和装配精度,减小变刚度机构的间隙,优化SMA弹簧的参数,则可进一步提高机械臂物理刚度的变化范围。
为验证上述变刚度的控制过程,设计了如图14的一个正面碰撞实验。在碰撞发生之前,碰撞标记C的默认值为0,按照3.2所述逻辑过程,在碰撞稳定之前机械臂始终处于低刚度状态。如图14显示了刚度控制的时序图,在t1时刻机械臂末端与障碍物初步接触,随后目标与机械臂之间的作用力逐渐增加直至t4时刻达到稳定,实验中设置约束主矩变化率阈值VM和主矢变化率阈值VF分别为1.5 N·m·s-1和6 N·s-1,在t1至t4期间,主矢变化率最高达到了8 N·s-1。由于是正面碰撞,对其主矩影响不大,根据上述的控制策略,图中t2时刻系统接收到碰撞信号,此时将碰撞标记C设置为1,而t3时刻当主矢变化率降至VF以下,系统判定碰撞结束,在此时控制系统模拟输出端提升输出电流至1.5 A,在短时间内机械臂刚度随着SMA温度的升高从3 N·m-1提升至14 N·m-1。通过本实验可证明该连续型机械臂物理刚度主动调控方法的可行性。
5 结 论
本文以兼顾空间操作的安全性和操作精度的需求为出发点,提出一种被动适应碰撞且能保证操作精度的可变刚度丝驱动连续型机械臂。以超弹镍钛合金丝为支撑脊椎和驱动部件的连续型机械臂具有优良的本体柔性,对接触碰撞具有较好的被动适应性。为克服操作过程中本体柔性对机械臂操作精度和承载能力的削弱,结合基本运动学分析和末端位置反馈设计了稳定的闭环运动控制器保证控制精度。另外,设计了一种调节内摩擦力的变刚度方法,在检测丝驱动力的基础上提出一种简化的碰撞识别和变刚度控制策略。实验证明机械臂能够较好克服外部干扰跟踪目标轨迹,具有良好的运动精度,并且可通过碰撞状态适应性地调控机械臂刚度来满足操作需求。本文初步提出并验证了一套在空间操作中具有潜在应用价值的物理可变刚度连续型机器臂设计、建模与控制方法,为连续型机械臂进入太空在轨服务进行了理论与技术的初步探究。为推动连续型机械臂在空间操作中的实际运用,未来工作将结合环境特征(高真空、大温差,强辐射等)和操作需求(目标的质量、体积、自旋、章动及安全操作距离等),进一步开展系统综合设计研究。
