基于POD算法的数据后处理应用程序
2019-01-07张青山陈伟民董国祥
张青山, 陈伟民, 董国祥
(上海船舶运输科学研究所 航运技术与安全国家重点实验室, 上海 200135)
0 引 言
尾流、射流和分离流等流体在流动过程中表现出的主要特征是具有不同空间尺度和时间尺度的相干结构。流体在流动过程中多主体结构的共同存在使得识别每个相干结构的时空特征具有一定的难度,这种识别在研究传热、传质和流动噪声等物理过程方面具有重要作用。近年来,大涡模拟(Large Eddy Simulation, LES)和直接数值模拟(Direct Numerical Simulation, DNS)的广泛应用及时间分辨粒子图像测速仪(Time Resolved-Particle Image Velocimetry, TR-PIV)的迅速发展使得以合理的空间分辨率和时间分辨率来精确捕获瞬时变化的流量成为可能,进而使得从大量的数值和试验数据中提取显著的相干结构更加显著、精确。
SIROVICH[1]和LUMLEY[2]的研究证实本征正交分解(Proper Orthogonal Decomposition, POD)在近几十年被广泛用于从流场中提取并确定相干结构。LUMLEY[2]、NOACK等[3]和LIU等[4]的研究结果表明,POD算法通过对采用快照序列计算得到的时间和空间相关矩阵进行对角化,能提取最有能量的结构,按照其自身的能量和相关结构的层次进行排序。MEYER等[5]使用立体PIV获得的横流中的湍流和射流的瞬时速度场进行POD分析,结果表明尾涡是主要的动力学结构,与喷流核心的强相互作用有关,而喷流剪切层旋涡是局部的,且不占优势。PROTHIN等[6]根据基于时间分辨立体粒子图像测速仪(TR-SPIV)获得的NACA0015翼型周围的流动,采用基于POD系数的相位平均来强调尾流的不稳定特性。DERI等[7]通过层析PIV测量得到的流场的三维POD重建,量化围绕薄平板埋藏在高雷诺数湍流中的三维相干涡旋结构。文献[8]~文献[11]基于PIV测量得到的平板绕流的二维流场,利用POD分解技术提取平板两侧及下游存在的大尺度相干结构,发现模态系数之间有一定的联系,可利用模型系数对流场进行相位平均分析。这些研究虽然能实现POD算法的功能,但需针对不同的数据结果作相应的调整,对于实际工程应用而言操作繁琐,不能保证便捷、迅速地实现。
本文基于POD基础理论开发POD的应用程序,设计输入模块、POD核心模块和输出模块,并采用C++语言编制核心代码;此外,为方便用户使用,采用QT设计用户界面,对功能模块和用户界面进行打包并形成应用程序包。
1 本征正交分解技术
POD作为一种处理大批量数据的方法,广泛应用于天气预报、图像识别、信号分析、数据压缩、随机过程和海洋学等领域中。POD分解可从系统已知的试验解或数值解中得到一系列基函数(这些基函数常被称作“模态”),并保证这些基函数在最小二乘意义下是最优的正交基函数。在湍流速度场研究中,POD分解能将相干结构及其包含的能量对应起来,从而使POD能用来识别湍流流场中各种能级的结构。LUMLEY[12-14]将POD引入到湍流研究领域中,通过对空间速度相关函数进行正交分解来识别流场中的相干结构。SIROVICH[1]通过对HOLMES等[15]提出的直接POD方法进行改进,提出快照方法(Snapshot POD)。该方法利用时空转换原理解决空间点数太多造成空间矩阵庞大而难以直接用POD求解的问题,使采用POD方法处理复杂流场成为可能。
POD的基本数学思想为:假设空间上有m个离散采样点x1,x2,…,xm,单次采样即可同时得到这m个离散点的值u(x1),u(x2),…,u(xm);共采集N次,得到空间场(u1(x1),u1(x2),…,u1(xm)),(u2(x1),u2(x2),…,u2(xm)),…, (uN(x1),uN(x2),…,uN(xm)),以矩阵的形式表示为
(1)
具体相关矩阵为
(2)
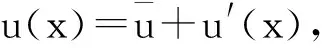
对时间相关矩阵的特征值和特征向量进行求解,有
CA=λA
(3)
式(3)中:特征值λ为非负实数;A为对应的特征向量。由此可构造特征函数
Φ=U·A
(4)

(5)
2 应用程序包的构成
POD数据后处理应用程序包由数据输入模块、POD数据处理核心模块和数据输出模块等3个功能模块组成(见图1)。

图1 POD数据后处理程序结构框图
1) 数据输入模块的主要功能是从外部磁盘中读取POD数据后处理所需的原始数据,包括文件列表管理(获取指定目录及子目录中的相关信息)、文件格式筛选(根据用户指定的格式提取相应格式的文件)、文件结构解析及读取(解析单个文件中的数据结构并读取数据)和数据转换(将从文件中读取的数据转为POD数据处理核心模块所需的类型)等4个子模块。
2) POD数据处理核心模块的主要功能是对数据进行POD分析,包括POD分解(进行POD分解计算,分别计算特征值、特征模态和模态系数)、POD重构(基于POD分解得到的特征值、模态和模态系数对流场进行重构)和相位平均(基于重构的流场进行相位平均,同时计算流场瞬态相位角和相位流场信息等)等3个子模块[4, 8, 10-11]。
3) 数据输出模块的主要功能是将POD分析得到的结构导入/保存到外部磁盘中,包含结果列表管理(根据用户选择的POD功能模块生成相应的文件列表)、输出格式管理(根据用户指定的格式筛选相应的数据转换方式)、数据转换(根据用户指定的格式对POD分析结果进行转换)和输出文件解析及保存(解析用户指定的格式,同时将转换后得到的POD分析结果保存到外部硬盘中)等4个子模块。
3个模块的相关代码都采用C++语言编制,模块之间的调用和相关的数据转换等都在程序内部实现,无需额外生成外部文件进行频繁的输入/输出操作。
为方便使用,采用QT语言设计用户交界面,避免用户误输出或误操作导致程序崩溃,基本的界面设计见图2。同时,为使用户熟悉程序的使用,在界面中添加提示子模块,在输入参数时提示用户,确保输入的参数正确和程序运行正常。此外,设计多线程管理功能,保证程序运行时主界面不卡顿。
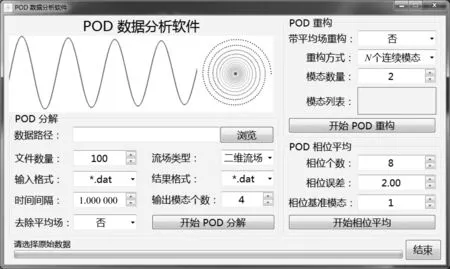
图2 POD数据后处理主体界面
3 POD数据后处理程序的验证
为验证POD数据后处理程序的可靠性,以经典的自由来流圆柱绕流为例,将POD数据后处理程序应用到8 000幅PIV测量得到的瞬态速度场中。
3.1 试验布置
PIV试验在一个低速循环水槽[17]中进行,试验段截面尺寸为100 mm×100 mm。直径D=8 mm的圆柱体直接横跨在试验段中,安装在半深的高度上。图3为PIV测试区域基本示意。自由来流速度为1 m/s。圆柱体的下游采用激光片光源照亮,采用高速相机拍摄,拍摄区域的大小为10D×8D。经过PIV互相关算法计算之后即可得到速度场。
3.2 POD流场分解
在界面中设定好原始数据所在目录、原始场数量、原始场类型、输入格式和输出格式等参数之后,开始进行POD分解计算,得到特征值、特征模态和模态系数等参数。
图4为前100阶POD模态对应的特征值,这些特征值代表对应模态所包含的能量。从图4中可看出,随着模态阶数的增加,特征值逐渐减小。前4阶POD模态的含能较高,因此提取前4阶POD模态并绘制速度云图(见图5)。从图5中可看出,前2阶POD模态为卡门涡街脱落,第3阶和第4阶POD模态与卡门涡街脱落有关。由此可知:特征值较大的模态对应的模态结构的空间尺度较大;特征值较小的模态对应的模态结构的空间尺度较小。因此,只需关注大尺度的流动结构即可。
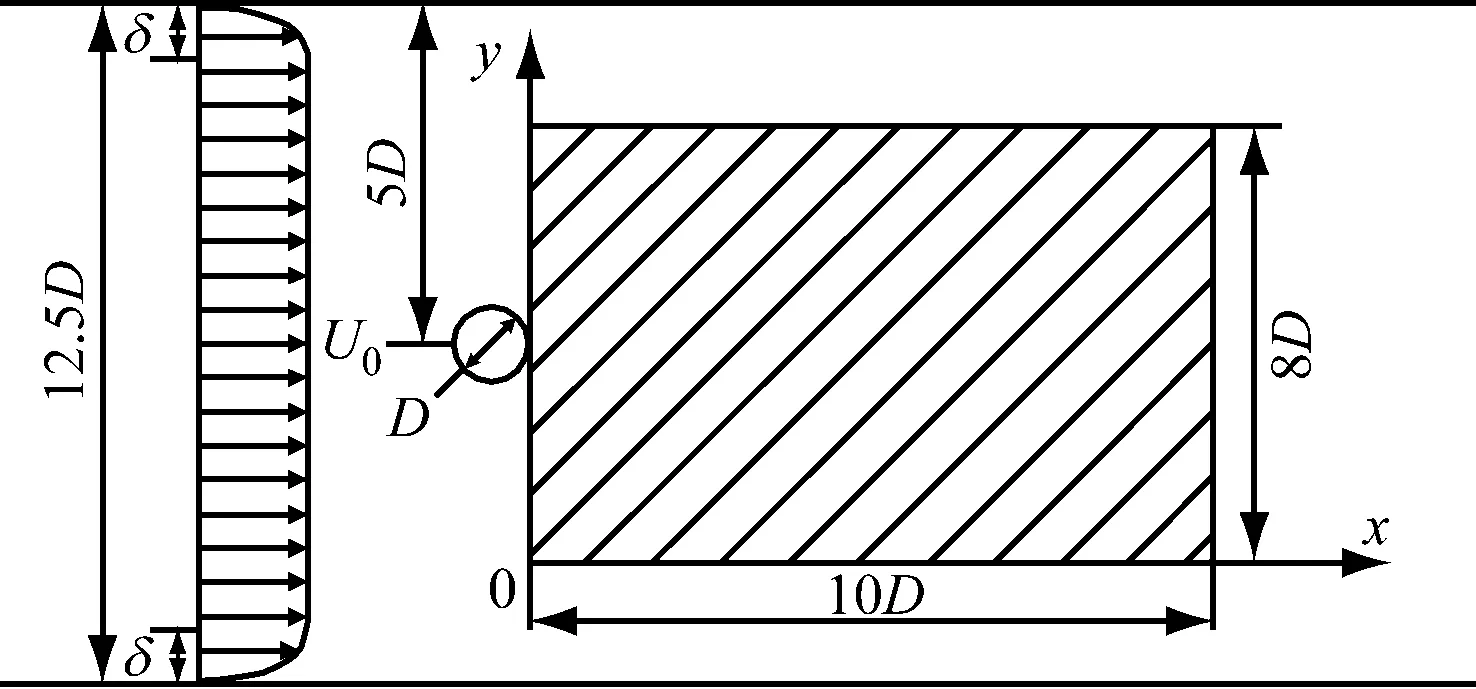
图3 PIV测试区域基本示意

b) 第2阶模态

c) 第3阶模态

d) 第4阶模态
图5从圆柱尾流中提取的前4阶POD模态
图6为前4阶POD模态对应的模态系数。从图6中可看出:前2阶模态系数呈现周期性变化规律,同时在时间上有一定的错位,看似存在一定的联系;后2阶模态系数同样有一定的周期性,这是因为其模态与卡门涡街有一定的相似之处,但周期性相对前2阶模态系数较差。

a) 第1阶模态系数
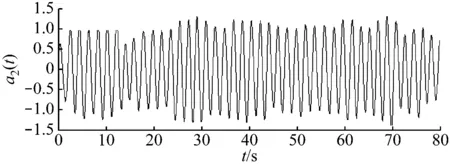
b) 第2阶模态系数

c) 第3阶模态系数
3.3 POD流场重构
由POD分解可知,圆柱尾流中包含复杂的流动,既有大尺度的卡门涡街结构,又有大量的小涡和散涡。为更加清晰地识别流场中的主导结构,基于POD数据后处理软件对流场进行重构,重构结果见图7。

a) 原始速度场U

c) 重构速度场U

d) 重构速度场V
通过比较发现:POD重构保留了原始速度场的整体特性,圆柱绕流下游的卡门涡街脱落现象基本上与原始速度场一致;同时,重构速度场剔除了尺度较小的旋涡结构,使得大尺度相关结构的空间结构更加光滑、突显。
3.4 相位平均
由上述分析可知,圆柱绕流尾流中卡门涡街呈现出周期性脱落的特征。由此确定,POD模态系数与旋涡脱落过程存在着一定的联系。OUDHEUSDEN等[18]在研究自由来流情况下方柱分离再附流动的流动特性时发现POD分解方法中前2阶模态系数与旋涡脱落过程之间存在特殊的关系,同时提出一种根据前2阶模态的系数确定流场中相关结构不同时刻相位的方法。因此,在进行相位分析是需有2个模态的系数,从而确定旋涡脱落过程中各时刻的相位角。
图8为卡门涡街脱落对应模态系数的相关分布。从图8中可看出,卡门涡街模态系数呈圆形分布。设定(0,0)为原点,即可将整个图像分成N等分的扇形,此时有N个相位角。本文选取8个相位角,并对流场进行相位平均。
图9为相位平均过程中参与每个相位角平均的流场个数。从图9中可看出,在8 000个瞬态场中,参与这8个相位角平均的流场的数量基本接近,为80~100个。
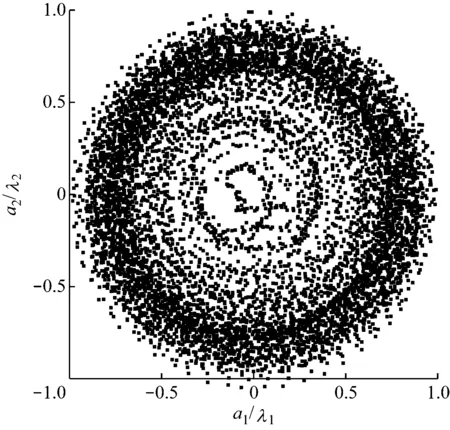
图8 卡门涡街脱落对应模态系数的相关分布

图9 相位平均过程中参与每个相位角平均的流场个数
图10为重构流场的法向速度场,给出了一个卡门涡街脱落周期内相同时间间隔的8个相位角的速度场,同时移除了平均场。从图10中可清晰地看到圆柱绕流尾流中卡门涡街交替脱落的特性,在向下游输运的过程中先逐渐增长,然后逐渐耗散。

a) T/8

b) 2T/8

c) 3T/8
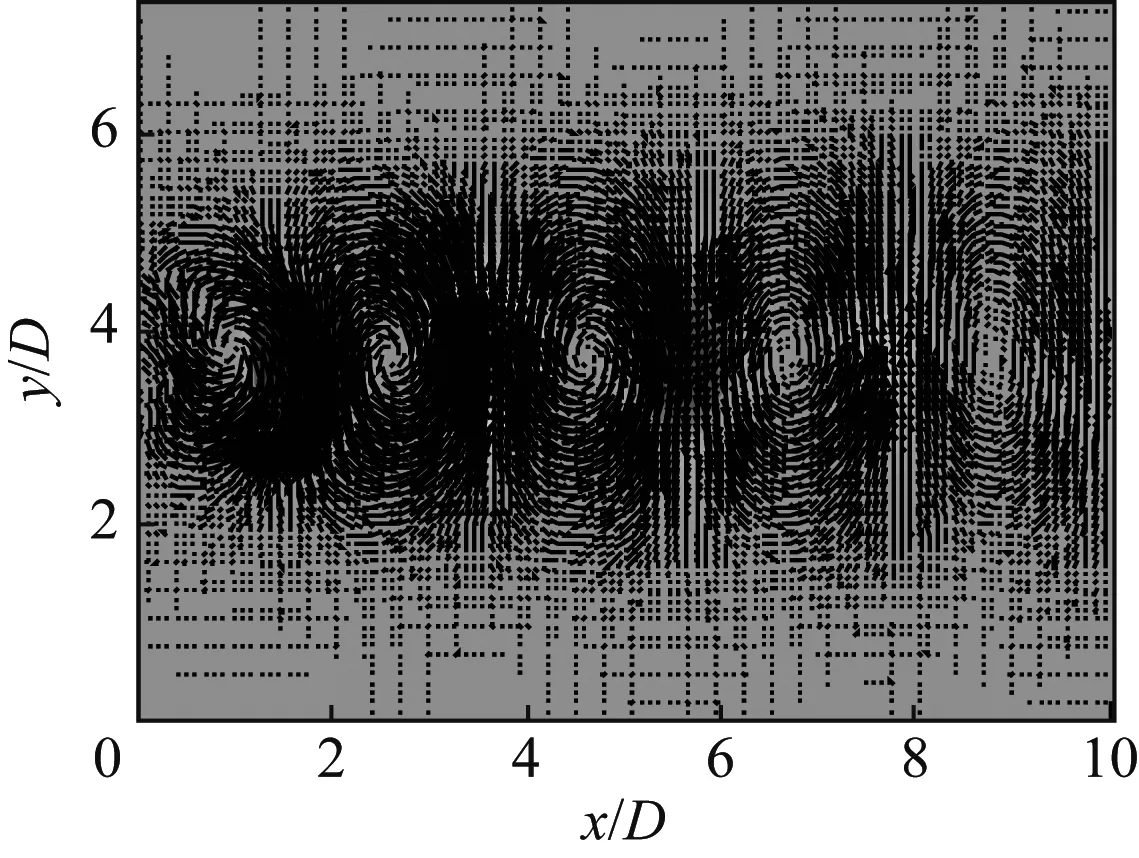
d) 4T/8
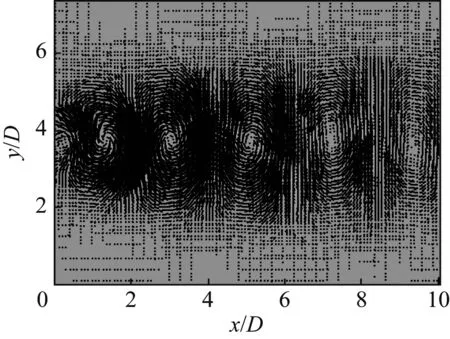
e) 5T/8

f) 6T/8

g) 7T/8
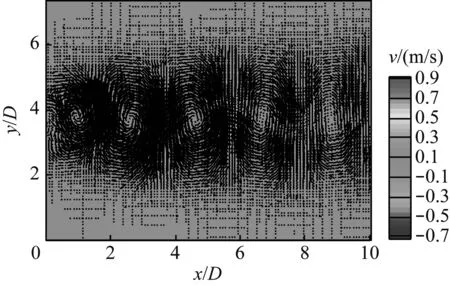
h) 8T/8
图10重构流场的法向速度场(移除时均平均速度场)
4 结 语
本文基于本征正交分解理论编制POD数据后处理程序,同时以经典的圆柱绕流为例验证POD数据后处理程序的各项功能,得到以下结论:
1) POD数据后处理程序运行稳定,在POD分析计算过程中不卡顿;
2) 程序的各子模块设定基本合理,能独立完成相应的功能,如输入模块只负责原始数据载入,POD核心模块负责POD分解、POD重构和相位平均,输出模块负责将POD分析结构导出到外部硬盘中;
3) POD数据后处理程序能很好地实现POD数据分解、POD数据重构和相位平均等功能;
4) 基于POD数据后处理程序,可获取更加丰富的流场信息,是研究流场的非定常特征的新方法。
