基于贝叶斯MCMC法的P-III分布估参效率比较

李 扬

（山西省水利水电科学研究院 山西太原 030002）

0 引言

水文频率分析工作是水利工程规划设计的基础，其中参数估计是洪水频率分析的重要部分，但未知参数的估计具有不确定性，结果的可靠性受到不确定性的影响，因此在参数估计中需要尽可能综合各种现有信息来进行统计推断。贝叶斯统计学与经典统计学的主要区别就是将先验信息加以利用，与样本信息结合来进行统计推断，可以更为客观全面地描述未知参数的统计特性。后验分布的推求是贝叶斯推断的关键步骤，但常常因其中的高维积分太过复杂而难以求解。马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，简称MCMC）方法是解决复杂积分问题的有效途径。本文选用3种MCMC抽样算法，结合实例对不同算法在P-III分布参数估计中的计算效率进行了比较和评估。

1 贝叶斯理论

基于总体信息、样本信息和先验信息进行的统计推断称为贝叶斯统计学，其与经典统计学的主要区别为是否利用先验信息。同时，贝叶斯学派重视已出现的样本观察值，不考虑尚未发生的样本观察值。先验信息是在抽样之前有关统计问题的一些信息，主要来源于经验和历史资料，经过挖掘、加工和数量化后形成的先验分布可用于后验分布的推求，基于后验分布对参数进行统计推断更为合理有效，因为后验分布可以看作人们用总体信息和样本信息对先验分布进行调整的结果，反映了人们在抽样后对参数的认识[1]。其基本观点是：将未知参数视为随机变量而非复杂的未知常量[2]。某站点洪水的密度函数f（x，θ）在贝叶斯统计中可记为f（x|θ），其中θ为未知参数矢量，表示在未知参数矢量给定某个值时，总体指标X的条件分布，设先验分布为 π（θ），则后验分布 π（θ｜x）的表达式为：

2 MCMC方法

马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，简称MCMC）方法[3]目前是处理复杂统计问题的有效手段，尤其在经常需要计算复杂高维积分的贝叶斯统计领域更是如此。在贝叶斯统计学中，高维积分主要用于求得普通方法无法获得的后验分布密度。MCMC方法的基本思想是通过建立一个平稳分布为π（θ）的马尔科夫链来得到π（θ）的样本，基于样本来进行各种统计推断。若定义和实施合理，马尔科夫链将会收敛，此时其极限分布即为后验分布。其步骤如下：

1）在观测样本上选择一个平稳分布为π（θ）的马尔科夫链，使其转移核为 f（*，*）；

2）由观测样本上的某一点θ0出发，用（1）中的马尔科夫链产生点序列θ1，…，θn；

3）对某个m和足够大的n，任一函数f（x）的期望估计如下：

可以看出采用MCMC方法时，构造转移核是至关重要的，不同的MCMC方法其实质是转移核的构造方法不同。

2.1 MCMC抽样算法

2.1.1 MH算法

Metropolis-Hastings（MH）抽样算法是通过服从建议分布的候选点γ获得t+1时刻的状态。一般要求建议分布的形式尽可能简单，易于计算，马尔科夫链下一个状态被接受为候选点的概率为：

抽样步骤如下：

1）给定初值 θ0，令 t=0；

3）从均匀分布［0，1］产生 U；

4）若 U≤α（Xt，γ），令 Xt+1=γ，否则 Xt+1=Xt；

5）令 t=t+1，重复步骤（2）～（5），直到产生足够的抽样样本为止。

2.1.2 DR算法

延迟拒绝（Delayed Rejection，DR）抽样算法中，目标分布为π时，对密度为的候选值θ*，其迭代接受概率为：

当θ*被拒绝时，下一个密度为q2（θ，θ*，θ**）的候选值θ**的迭代接受概率为：

2.1.3 AM算法

与MH算法和DR算法相比，自适应Metropolis（Adaptive Metropolis，AM）抽样算法并不需要指定参数的建议分布，而是由后验参数的协方差矩阵在每一次迭代后自适应地调整来得到参数样本[4,5]，其抽样步骤如下：

1）初始化t=0，给定协方差矩阵C0；

2）在每一步迭代中产生新参数θ*；

4）产生[0，1]区间均匀分布随机数r，确定接受新参数，即

5）重复步骤（2）～（4），直到产生足够的抽样样本为止。

2.2 MCMC方法的收敛性诊断

MCMC方法的收敛性诊断方式有多种，方法一是对多个初值产生多个马尔科夫链，观察历史迭代图，波动幅度稳定时说明收敛；方法二是观察遍历均值，在得到的马尔科夫链中每隔一段距离计算参数的遍历均值，当这样算得的均值稳定时，可认为抽样收敛；方法三是方差比收敛性诊断，当方差比曲线稳定在1.0左右时说明抽样收敛。本文采用陆乐等[6]提出的EM（Ensemble Mean）和 ES（Ensemble Spread）两个指标来诊断样本是否收敛，当样本序列的EM和ES值稳定时认为抽样收敛。

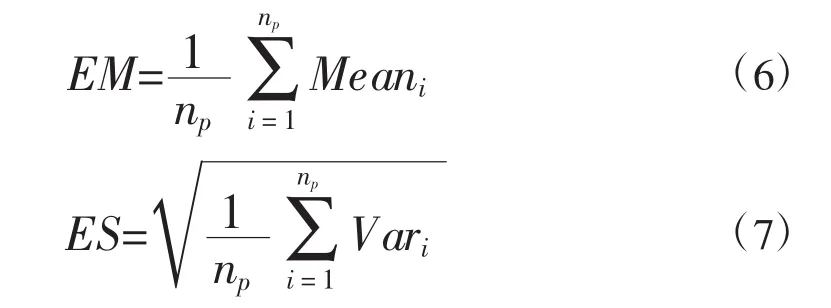
式中，np为参数个数，Meani和Vari分别为第i个参数样本序列的均值和方差。

3 P-III分布参数的贝叶斯估计

P-III分布的概率密度为：

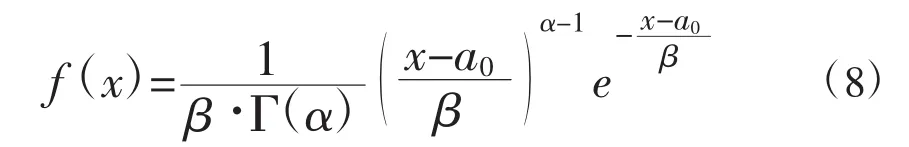
式中，Γ（·）为 gamma函数，α、β、ɑ0分别为形状、尺度和位置参数。它们与样本均值x、变差系数Cv和偏态系数Cs的关系为：

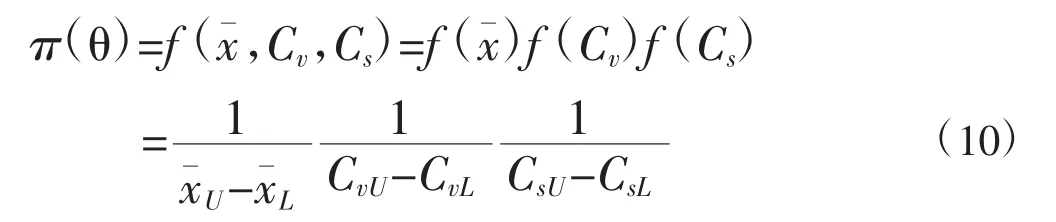
后验分布为：

使用MH算法和DR算法抽样时，选取多元正态分布为建议分布。

4 应用实例

为比较不同MCMC抽样算法的计算效率，选择陕北地区刘家河、神木等5个水文测站的年最大洪峰流量系列资料进行应用，资料概况如表1所示。

设置模拟抽样次数为15 000次，通过Matlab编制程序，采用MH、DR和AM三种抽样算法分别进行模拟抽样，获得模拟参数样本系列。所得样本序列的EM、ES曲线及经验频率和理论频率拟合结果如图1～图5所示。

表1 陕北地区5个测站洪峰流量系列长度

图1 刘家河站EM-ES-累积概率比较

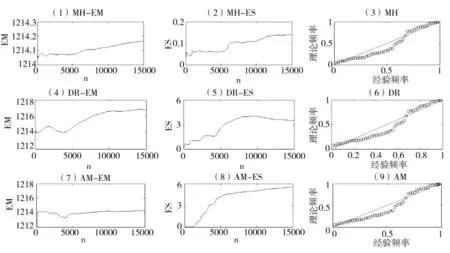
图2 神木站EM-ES-累积概率比较

图3 绥德站EM-ES-累积概率比较

图4 赵石窑站EM-ES-累积概率比较

图5 志丹站EM-ES-累积概率比较

由图可知，当产生15000个参数样本后，刘家河站AM抽样的ES值大约稳定在2.5左右，且抽样次数不足5 000次时曲线便已稳定，DR抽样的ES值在2.0附近波动，而MH抽样的ES曲线仍呈上升趋势，说明马尔科夫链尚未收敛到参数的后验分布；EM曲线趋势与ES曲线相同，其余各站情况类似，即在同等抽样次数下，AM抽样的ES值最早达到稳定，收敛最快，DR抽样的结果次之，MH抽样在试验次数内无法收敛到参数的后验分布。对于理论频率和经验频率的拟合结果，由图可知，三种抽样方法的结果基本相同，可认为不同抽样算法对参数样本的频率拟合效果没有影响。

5 结论

本文基于贝叶斯方法，比较了不同MCMC抽样算法对P-III分布参数估计的效率，结论如下：

1）分别采用MH、DR、AM抽样算法时，AM算法最快收敛，DR算法次之，MH算法收敛最慢，其中AM算法不依赖于参数的建议分布，能够获得较快收敛速度，且收敛指标曲线最为平稳，显著优于其余2种算法。

2）不同算法抽样对所得参数样本经验频率和理论频率的拟合效果没有影响。