基于非饱和-饱和渗流的降雨入渗边坡稳定性分析

2019-01-05董建军王思萌杨晓萧聂兰磊

水利与建筑工程学报 2018年6期

董建军，王思萌，杨晓萧，聂兰磊

(1.辽宁工程技术大学土木工程系，辽宁葫芦岛 125105；2.大连理工大学工程力学系，辽宁大连 116024；3.保定市城建规划工程设计研究院，河北保定 071000；4.山东同圆设计集团有限公司，山东济南 250101)

作为温室效应导致的全球变暖的后果，极端降水事件发生的频率显著增加，而且强度也显著增强，由此导致了大量的自然和人工边坡的破坏失稳，造成了巨大的生命和财产损失。而雨水入渗是最主要的诱因和决定因素。土质边坡的表层在受到雨水入渗的作用之后，土体的含水量将会逐渐增加，直至由非饱和状态转变为饱和状态，使得非饱和状态下的基质吸力逐渐消散，最终表现为土体的抗剪强度降低[1-2]。进行降雨条件下边坡稳定性分析，要更多的研究非饱和-饱和渗流特性和非饱和土强度、变形等规律。

近些年来，许多学者做了大量关于非饱和渗流以及降雨入渗条件下的土质边坡稳定性的研究工作。最初由学者Richards构建了非饱和的渗流方程[3]，并认为在非饱和土中水的运动特性是仍然遵循Darcy定律的，但在该状态下土体的渗透系数是与体积含水率存在内在联系的函数而非常量[4]。1973年Neuman[5]采用Galerkin型有限元方法求解饱和-非饱和多孔介质中瞬态渗流的拟线性偏微分方程，发现在处理通过土壤的瞬态渗流时，自由表面的经典概念并不总是适用。黄月华等[6]指出径流补给作用下地下水位将显著上升，其安全系数与不考虑径流补给条件下的安全系数降低明显。此外，Sun等[7]认为降雨入渗过程是雨水在入渗的过程中驱替空气的行为，是一种水-气二相流过程。

在降雨入渗条件下的土质边坡稳定性研究方面，Ali等[8]通过研究与完全排水、部分排水和不透水的边界相对应的破坏时间和深度，研究边界条件对滑坡的影响，结果表明边界条件可以显著影响降雨诱发滑坡的发生和深度。李宁等[9]提出了一个既考虑坡面倾斜影响，又考虑非饱和土特性的简化型降雨入渗模型。邢小弟等[10]建立了土体抗剪强度、降雨入渗时间以及土体含水率之间的函数关系，使之能够体现边坡土体含水率变化引起的土体强度降低现象。石振明等改进了G-A入渗模型，提出了一种适合多层非饱和土边坡降雨入渗的计算方法[11]。王宁伟等[12]通过建立水-土-气三相渗流-变形耦合有限元计算程序模拟了边坡失稳过程中的大变形问题。张社荣等[13]采用的方法是首先通过概化典型边坡数值模型，然后进行饱和-非饱和边坡的瞬态渗流场与应力场的耦合分析。詹良通等[14]通过在自行研制出的离心机机载降雨模拟装置上模拟研究了50g重力下非饱和粉土边坡在不同降雨强度下的失稳破坏过程，得出了具有普遍理论和工程意义的降雨诱发非饱和粉土边坡的失稳模式。

本文基于土质边坡非饱和-饱和渗流和DP5本构模型，并进行相关参数转化，引入非饱和土基质吸力分量，利用非饱和土的抗剪强度方程和渗流方程，通过数值计算方法，研究了降雨条件下雨水入渗过程中非饱和-饱和渗流场与应力场耦合作用下的边坡稳定性，从而为工程实践提供有效实用的方法。

1 本构关系

1.1 非饱和土抗剪强度方程

Vanapalli等[15]通过理论演绎和试验验证，提出了基于两个独立应力状态变量的非饱和土抗剪强度方程，方程形式如下：

τf=[c′+(σn-ua)tanφ′]+(ua-uw)(Θftanφ′)

(1)

式中：(σn-ua)为净法向应力；Θ=θ/θs为归一化体积含水率；θ为体积含水率；θs为饱和体积含水率；τf为土体破坏时，破坏面上的剪应力；c′为有效黏聚力；φ′为有效内摩擦角；ua为孔隙气压力；uw为孔隙水压力。

若不采用拟合参数f，Vanapalli等给出了如下表达式：

τf=[c′+(σn-ua)tanφ′]+(ua-

(2)

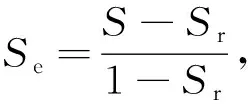
τf=[c′+(σn-ua)tanφ′]+Se(ua-uw)tanφ′

(3)

当孔隙气压力与孔隙水压力大小相同时，式(3)为饱和抗剪强度公式。式(3)与邵龙潭等[16]的非饱和土的土骨架应力方程及黄强等[17]基于混合物理论和热力学原理推导出的非饱和土有效应力方程一致。

根据式(3)定义总黏聚力表达式为：

ct=c′+Se(ua-uw)tanφ′

(4)

式中：ct为总黏聚力，而非总应力黏聚力。

采用基于非关联流动法则与M-C准则精确匹配的DP5准则，在饱和土的DP5模型中引入基质吸力分量与总黏聚力公式(4)，可得到用于分析非饱和土的力学特性的DP5模型关系式：

(5)

k=ct·cosφ′

(6)

式中：α，k为—DP5模型中与M-C模型中的内摩擦角与黏聚力相关的强度参数。

由试验确定的土体物理力学参数如表1所示。

表1 土体物理力学参数

1.2 非饱和土渗流方程

土体的非饱和-饱和渗流方程可用下面的张量形式表示：

qi=-kr(S)Kijh,j=kr(S)Kij[ψ+z],j

(7)

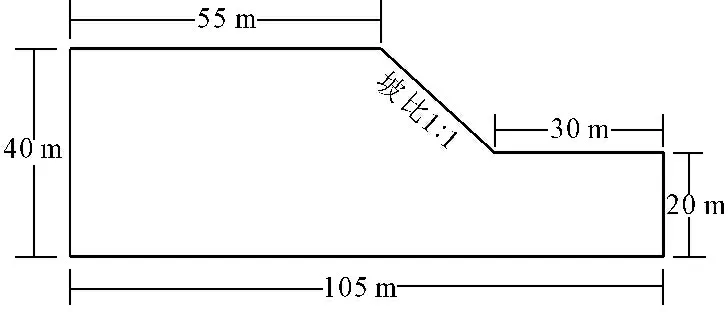
式中：qi为单位流量向量；Kij为渗透系数张量；kr(S)为相对渗透系数，饱和区kr(S)=1，非饱和区0

式(7)表明，土体的饱和渗流与非饱和渗流的方程表达形式是一致的，饱和渗流就是饱和度为1时的非饱和渗流。进行土体非饱和渗流分析的核心问题在于建立非饱和渗透系数与饱和度之间的函数关系，且土体非饱和区域的基质吸力在实际状态下表现为负的孔隙水压力。

在众多预测非饱和土渗透系数的模型中，最实用的是VG-M模型，其方程为

(8)

式(8)是Van Genuchten(VG)土-水特征曲线(SWCC)模型与Mualem(M)渗透系数模型[18-19]结合在一起的结果，其中VG模型的方程为

(9)

式中：ku为非饱和渗透系数；k为饱和渗透系数；n，a和m为VG模型拟合参数；s为基质吸力。

基于以上理论体系，在FLAC3D平台中通过FISH语言二次开发定义了非饱和土强度-渗流计算模型。

1.3 安全系数的计算

强度折减法的关系式为：

cF=ct/Ftrial=[c′+Se(ua-uw)tanφ′]/Ftrial

(10)

φF=tan-1(tanφ′/Ftrial)

(11)

kF=[k/cosφ′-Se(ua-uw)tanφ′]/Ftrial

(12)

αF=tan-1[tan(arcsin3φ′)/Ftrial]

(13)

式中：cF为折减后的总黏聚力；φF为折减后的内摩擦角；kF为折减后的DP5总黏聚力；αF为折减后的DP5内摩擦角；Ftrial为折减系数。

结合非饱和-饱和土的强度理论，安全系数的表达式为：

(14)

2 数值计算分析

2.1 数值模型建立和参数确定

建立的非饱和土边坡模型尺寸示意图如图1所示。

图1边坡尺寸示意图

三维模型的长度为105 m，高度为40 m，厚度为40 m，坡率为1∶1，边坡土质为完全固结土，数值模型单元数为76 600个。

由文献[20]中的试验结果，可以绘制土-水特征曲线(SWCC)如图2所示，再基于VG模型拟合出体积含水率与基质吸力的理论关系曲线，进而就能够确定VG模型的拟合参数，如表2中所列。从土-水特征曲线(SWCC)可以看出，在残余体积含水率11.90%至天然体积含水率23.87%的区间内，基质吸力曲线呈断崖式陡降；在天然体积含水率23.87%至进气值体积含水率48.75%的区间内，基质吸力曲线呈滑梯式下降；在进气值体积含水率48.75%至饱和体积含水率50.29%的区间内，基质吸力曲线也呈断崖式陡降。土-水特征曲线(SWCC)规律表明，体积含水率的增加必然导致基质吸力的降低，但基质吸力降低的速率与指标体积含水率所划分的区间相关，总体上可划分残余体积含水率θr-天然体积含水率θi、天然体积含水量θi-进气值体积含水率θb和进气值体积含水率θb-饱和体积含水率θs三个区间，各区间基质吸力降低的速率是明显不同的。由此可以确定，在降雨入渗过程中，随着雨水入渗，土质边坡土体的基质吸力降低将是一种复杂的非线性变化。

图2 土-水特征曲线(SWCC)

由此，基质吸力和体积含水率的关系式为：

(15)

由文献[20]的试验数据能够定义总黏聚力方程的具体表达式，则式(4)可以整理为：

(16)

非饱和土中水的流动性非常复杂。土体的性质、水的储存、蒸发以及瞬时渗透均与水的流动性有关。非饱和渗流参数如表3所示。

表3 非饱和渗流参数

降雨过程中，持续最大降雨量为3.46×10-6m/s，持续降雨时间为96 h，持续降雨过程的雨量变化曲线如图3所示。

在垂直渗透的情况下，斜坡降雨强度需要转化。边坡模型的法线方向的降雨强度为3.46×10-6m/s，通过转化，坡面法线方向的降雨强度为1.82×10-6m/s。

外部环境的变化对基质吸力影响较大，为了理解渗流对基质吸力分布的影响，非饱和土的基质吸力分布形式采用静水压力的分布形式，其随深度变化的分布规律如下图4所示。

图3 降雨强度的变化规律

图4非饱和土吸力水头的分布

2.2 数值分析结果

降雨前后土质边坡非饱和-饱和渗流场的计算结果如由图5所示。从图5(a)中可以看出，雨水入渗前，土质边坡的地下水位线即为孔隙水压力0值线；地下水位线以上的土体处于非饱和状态，孔隙水压力为负值，按逆向静水压力梯度分布；地下水位线以下的土体处于饱和状态，孔隙水压力为正值，按正向静水压力梯度分布。随着雨水入渗，从图5(b)—图5(e)中可以发现，相对于雨水入渗前的非饱和状态下的存在明显不同，土质边坡表层土体由非饱和转变为饱和，土体中的孔隙水压力由无雨水入渗前的负值变为按照静水压力分布的正值，土体中的基质吸力减小。并且随着降雨时间的增加，逐渐向边坡内部扩散，湿润锋面上的负孔隙水压力按梯度重新分布。

降雨过程中，随着雨水持续入渗，土质边坡的非饱和表面逐渐饱和。如图6中所示，降雨持续24 h～48 h期间，雨水入渗的深度还比较浅，边坡滑移破坏开始在表层出现，滑移区域的范围为由非饱和转变为饱和的土层底部附近，由于影响范围有限，边坡整体上处于稳定状态。降雨持续72 h和96 h，由于雨水入渗时间持续增加，雨水入渗的深度进一步扩大，边坡稳定性逐渐降低，边坡发生破坏失稳，滑移破坏从浅层渐近向深层发展。

图5孔隙压力的变化规律

不同降雨时间的的塑性区发展如图7所示，降雨持续24 h，塑性破坏从坡脚发生，形成的塑性破坏区域范围较小；降雨持续48 h，塑性破坏从坡脚向上扩展，形成的塑性破坏区域范围扩大；降雨持续72 h，塑性破坏区域加速从坡脚扩展到坡顶形成贯通，K=0.93，边坡破坏失稳。这与文献[14]通过离心机试验所揭示的降雨诱发粉土边坡的失稳模式是一致的。通过分析比较72 h和96 h的塑性区能够发现，随着入渗区域加深，塑性区贯通区域向深部发展。

3 结果分析

随着降雨时间的增大，土体抗剪强度降低，边坡安全系数降低，边坡不稳定性增加。基于图8的安全系数K与降雨历时t关系曲线，通过作图分析可以得到，在当前的降雨强度下，安全系数K=1.0的直线与关系曲线的交点所对应的降雨历时t1.0，即为降雨持续时间的界限时间为60.5 h。当降雨持续时间少于60.5 h，虽然历经非饱和-饱和渗流作用，基质吸力对边坡土体的抗剪强度贡献减小，但尚不足以对土质边坡的整体稳定性造成影响，因此各降雨时段土质边坡安全系数K>1.0，边坡始终处于稳定状态；当降雨持续时间达到60.5 h时，在非饱和-饱和渗流作用下，基质吸力对边坡土体的抗剪强度贡献持续减小，对土质边坡的整体稳定性产生影响，此时土质边坡安全系数K=1.0，边坡处于极限平衡状态；当降雨持续时间超过60.5 h时，非饱和-饱和渗流的作用显著，基质吸力对边坡土体的抗剪强度贡献变弱，对土质边坡的整体稳定性产生显著影响，此时土质边坡安全系数K<1.0，边坡发生破坏失稳。