钢筋混凝土矩形空心墩延性能力数值分析

刘志峰，王同珍，罗 征

(1.济南市公路管理局， 山东 济南 250014； 2.济南职业学院 机械制造学院， 山东 济南 250014；3.浙江大学 宁波理工学院 土木建筑工程学院， 浙江 宁波 315000)

近年来，钢筋混凝土空心墩在大跨径高墩桥梁中应用较多，但关于空心墩的抗震性能方面的研究较少，故本文针对钢筋混凝土空心墩的延性能力进行了分析。

延性是混凝土桥墩的一个重要性能[1]。现在的国内外学者对空心墩的配筋率、配箍率以及轴压比对墩柱的延性能力的影响进行了多方面的研究，长安大学崔海琴等[2]和北京工业大学杜修力等[3]以及同济大学宋晓东[4]分别对矩形空心墩柱进行了拟静力试验；以壁厚、配筋率等为研究参数，提出了各参数对延性能力的影响。但对不同剪跨比下各方面影响研究的很少。本文通过有限元分析软件Opensees建立合理数值计算模型，研究分析了不同剪跨比下配筋率、轴压比、壁厚、混凝土强度及纵筋强度等参数对空心墩柱极限承载力与延性变形能力的影响。

1 钢筋混凝土矩形空心墩拟静力试验

本文分别对4个矩形空心墩进行了拟静力试验，试件编号分别为 201、603、704、706，其截面相同，几何尺寸见图1；混凝土采用C40，纵筋及箍筋均为Ⅱ级钢筋见图2；各试件的参数见表1[5]。试件分为两个组，分别研究分析不同剪跨比和配箍率的影响。

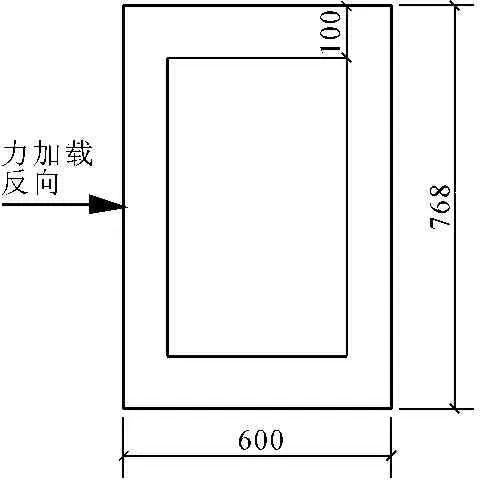
图1截面几何尺寸图(单位：mm)

这里需要特殊指出的是，国内采用的混凝土强度为立方体轴心抗压强度，而在数值计算时需要将其换算为圆柱体抗压强度。本文以位移延性能力作为检验空心墩柱变形能力的性能指标，为了计算桥墩的延性变形能力，在确定桥墩的等效屈服位移后，尚须确定其极限状态。

本文采用以下首先达到极限状态(抗压强度下降到80%、纵筋屈曲断裂或核心混凝土破坏)的墩柱来确定承载能力。

图2 钢筋构造图(单位：mm)

试验墩柱的位移延性能力如表2[5]所示：(1) 4个钢筋混凝土矩形空心墩抗震性能良好；(2) 配箍率不变的情况下，空心墩柱的极限承载力和延性能力随剪跨比的减小而有所提高；(3) 剪跨比相同，配箍率的提高使空心墩的极限承载力与墩柱位移延性能力都有提高。

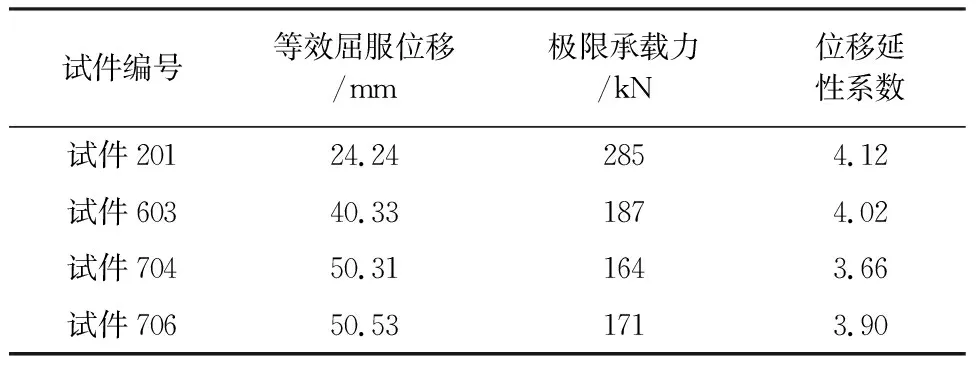
表2 矩形空心墩位移延性能力

尽管试验研究了剪跨比、配箍率等参数对空心墩柱抗震性能的影响，但配筋率、轴压比、壁厚、纵筋强度等参数对空心墩柱抗震性能的影响尚未可知。本文首先将建立纤维有限元模型，利用4个空心墩柱的试验结果验证纤维模型的正确性。

2 纤维单元模型

2.1 混凝土材料本构

约束混凝土与无约束混凝土材料应力-应变关系采用Opensees材料库中的Kent-Park提出的Concrete01模型[6-7]，该模型是Kent等人通过大量矩形箍筋墩柱的试验提出的，并在实践中得到了广泛应用。

2.2 钢筋本构

钢筋材料应力-应变关系采用Opensees材料库中Mander与Chang所提出的等向强化非线性钢筋模型ReinforcingSteel[6，8]。在Mander钢筋模型基础上，本文选用Coffin-Manson模型[9]，考虑由于低周期疲劳引起的钢筋强度和刚度退化，该模型主要由3个参数控制：损伤累积系数α、疲劳延性系数Cf、疲劳强度退化系数Cd。Brown[10]的钢筋低周疲劳材料试验研究得出上述三个参数的推荐值分别为：α=0.506，Cf=0.26，Cd=0.389；图3为考虑低周期疲劳后钢筋材料滞回曲线。

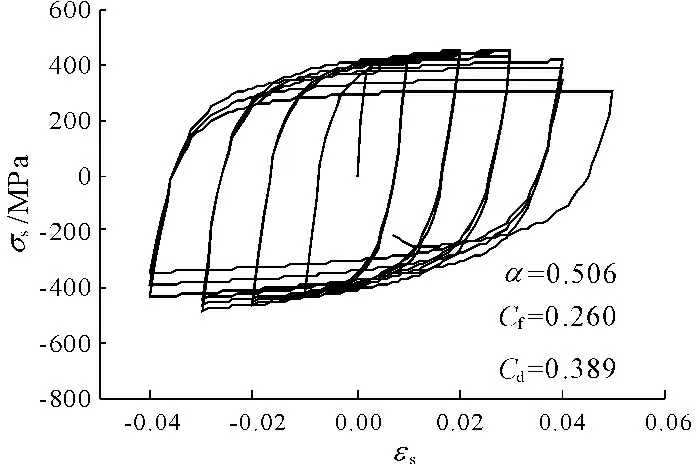
图3 Coffin&Manson钢筋应力-应变滞回曲线

3 数值模型验证

采用OpenSees 建立矩形空心墩的纤维单元模型，对4个矩形空心墩柱在考虑强度退化和粘结滑移的情况下的墩顶位移进行数值模拟，如图4、图5所示。

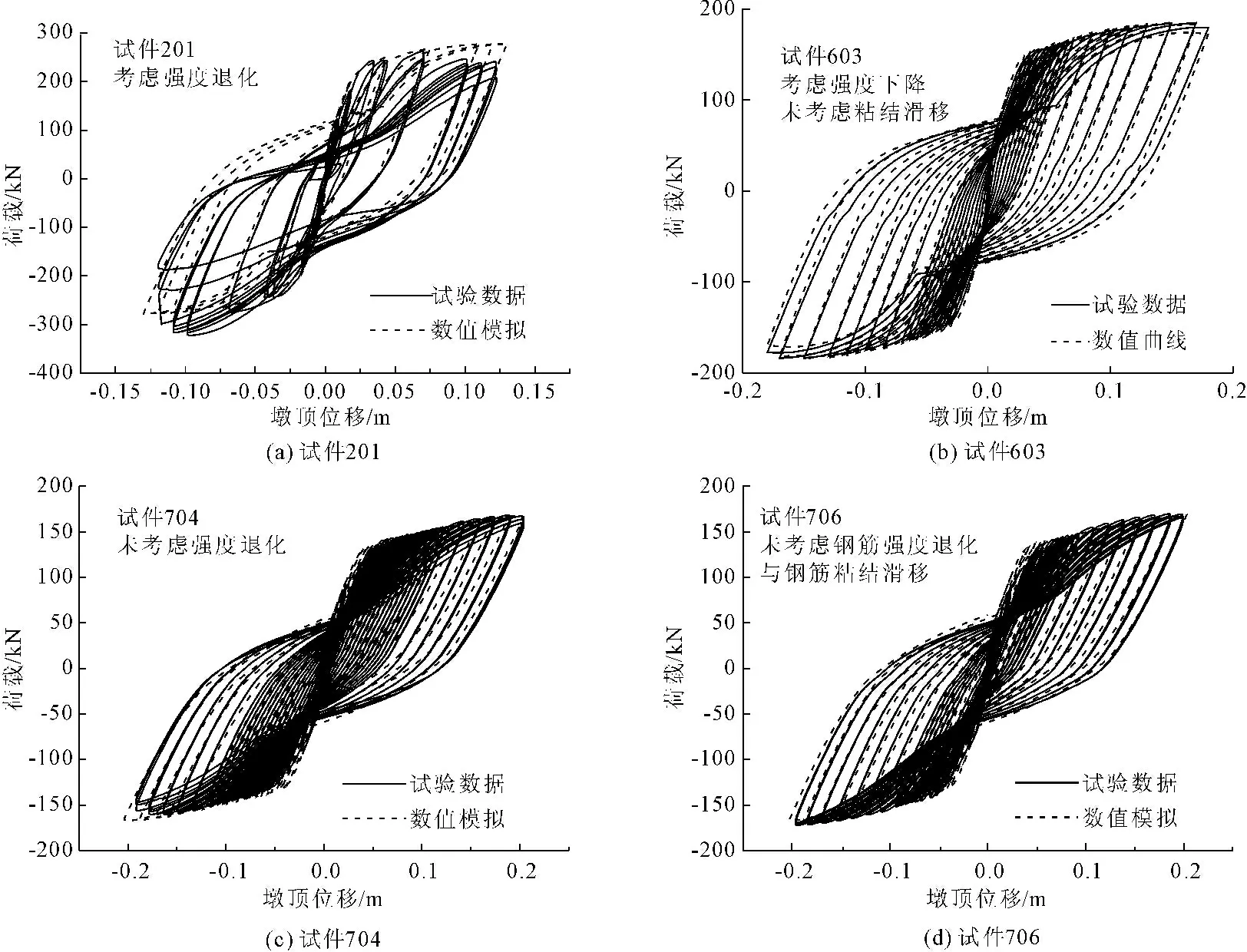
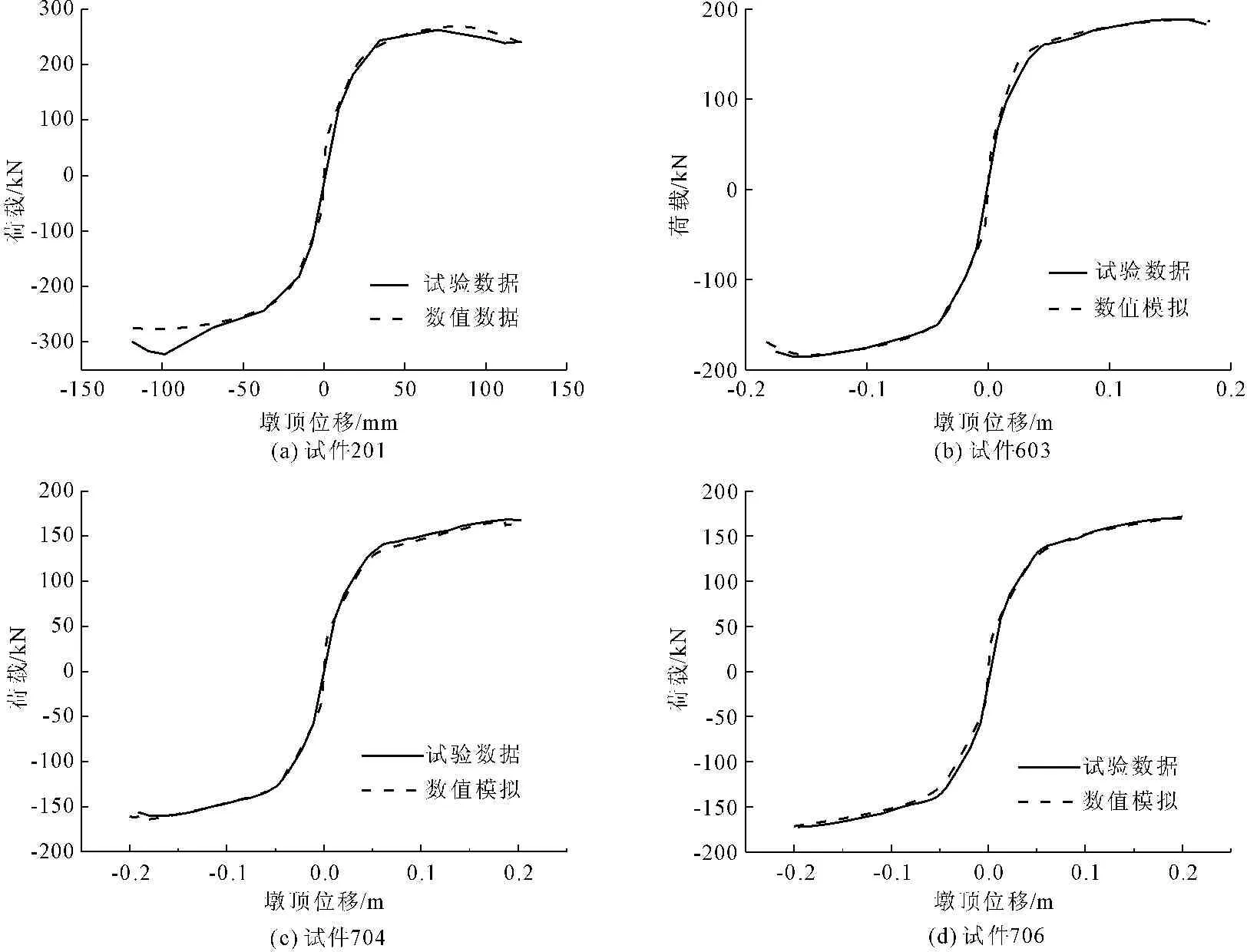
图4 数值模拟与试验数据滞回曲线对比

图5数值模拟与实验数据骨架曲线对比

从图4、图5可以看出，各空心墩试件滞回曲线与骨架曲线的计算值与试验值较为吻合，说明混凝土采用Kent-Park本构模型，纵筋采用Mander-Chang本构模型，同时模型中考虑钢筋的强度退化，纤维模型可对钢筋混凝土空心墩滞回性能进行较为准确模拟分析，验证了纤维模型的正确合理性。

4 空心墩延性变形能力参数分析

下面对可能影响矩形空心墩变形能力的参数进行敏感性分析，孙治国等通过有限元模拟，采用位移角作为延性目标对圆形空心墩的延性性能进行了研究。但国内对于桥梁结构而言，一般采用位移延性能力作为检验墩柱延性能力的指标。固本文采用位移延性能力作为延性指标，对纵筋配筋率、壁厚、轴压比及纵筋强度等参数对矩形空心墩抗震能力的影响。

4.1 纵筋配筋率的影响

取剪跨比λ为4、轴压比ηk为0.1、壁厚t为100 mm，不同配筋率的三种矩形空心墩，矩形空心墩主筋配筋率分别为0.96%、1.93%、2.93%，进行Pushover分析，其对应的能力曲线如图6所示，配筋率提高一倍，空心墩承载能力可提高75%左右，但位移延性随着配筋率的增大而减小。

图6不同配筋率骨架曲线

矩形空心墩壁厚为100 mm，不同轴压比、不同剪跨比时，空心墩位移延性随纵筋配筋率变化情况见图7。随着纵筋配筋率提高，不同轴压比及剪跨比的空心墩延性变形能力曲线基本呈降低趋势。

4.2 壁厚的影响

取剪跨比λ为4、配筋率ρl为0.96%、轴压比ηk为0.1，不同壁厚t的三种矩形空心墩，三种矩形空心墩壁厚，分别为100 mm、200 mm、300 mm，进行Pushover分析，其对应的能力曲线如图8所示，不同壁厚的空心墩骨架曲线重合，空心墩壁厚的提高对空心墩的承载能力及位移延性能力影响不大。这一点与孙治国的研究成果有出入，究其原因是由于剪跨比的不同，对于剪跨比小于4的矮墩[11]而言，位移延性能力随着壁厚的提高而减小，而本文中对于剪跨比大于4的高墩而言，壁厚的变化对延性延性影响不大。

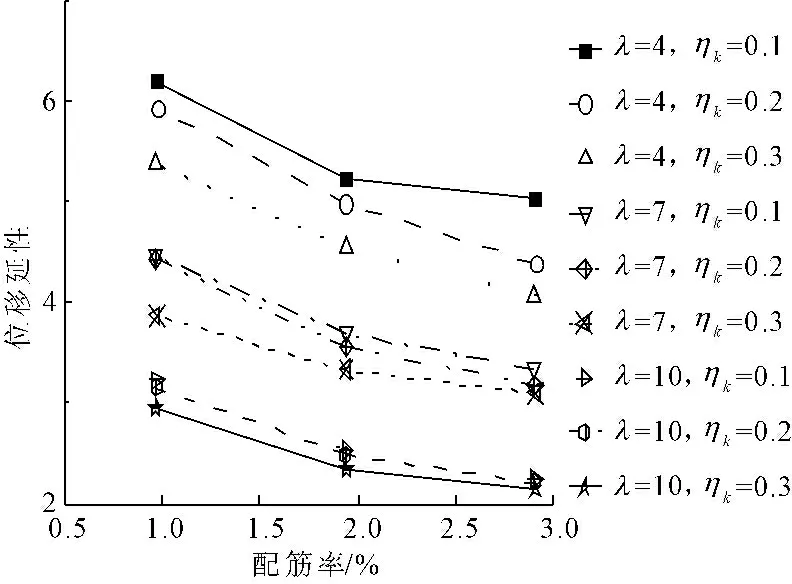
图7 壁厚不变，配筋率对矩形空心墩延性变形性能影响

图8不同空心墩壁厚骨架曲线

矩形空心墩配筋率为0.96%，不同轴压比、剪跨比(剪跨比大于4的墩)时，空心墩位移延性随空心墩壁厚t与空心墩边长b之比变化如图9所示。在轴压比、纵筋配筋率不变的情况下，壁厚变化对空心墩极限变形能力影响不大[12]，空心墩延性变形能力基本保持稳定。

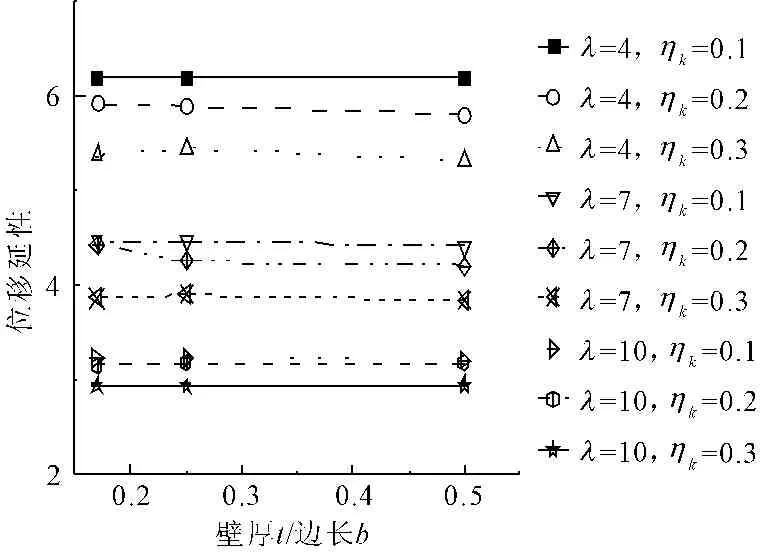
图9壁厚对矩形空心墩延性变形性能的影响

4.3 轴压比的影响

取剪跨比λ为4，配筋率ρl为0.96%、壁厚t为100 mm，不同轴压比ηk的三种矩形空心墩，轴压比分别为0.1、0.2、0.3，进行Pushover分析，其对应的能力曲线如图10所示，由图10可知，轴压比增加1倍，空心墩的承载能力增加近50%，同时空心墩位移延性随着轴压比的提高而有所降低。

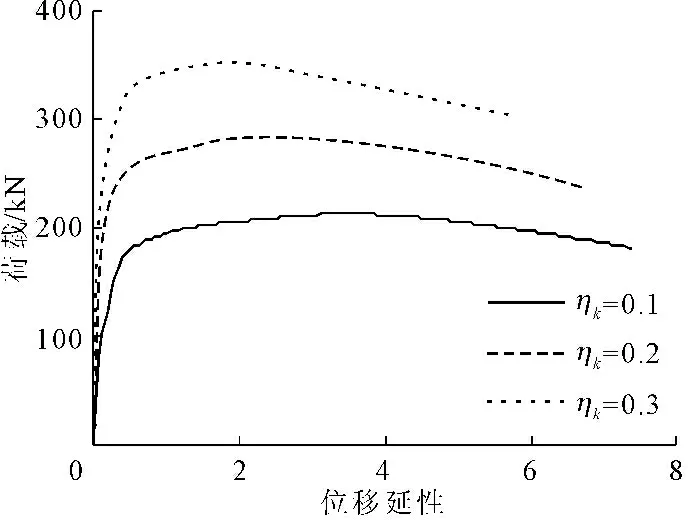
图10剪跨比、配筋率和壁厚不变，不同轴压比骨架曲线

矩形空心墩壁厚为100 mm，在不同配筋率、剪跨比，空心墩位移延性随轴压比变化情况见图11，壁厚不变，配筋率、剪跨比不同的情况下，空心墩延性变形能力随轴压比的提高而降低。

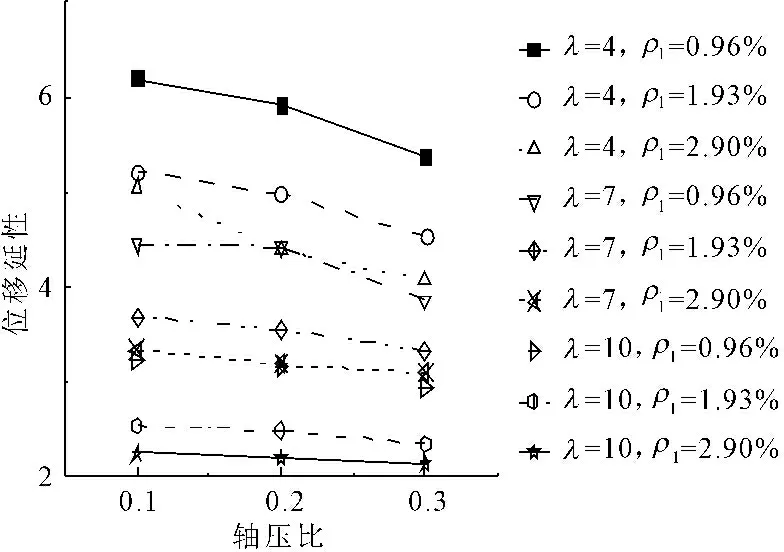
图11配筋率、剪跨比不同，轴压比对矩形空心墩延性变形性能影响

4.4 纵筋强度的影响

取剪跨比λ为4，轴压比ηk为0.1，配筋率ρl为0.96%在不同纵筋强度的三种矩形空心墩，纵筋强度分别为464 MPa、507 MPa、542 MPa，进行Pushover分析，其对应的能力曲线如图12所示，由图12可知，纵筋强度的提高对空心墩的承载能力有所提高，但空心墩位移延性随着纵筋强度的提高而减小。

矩形空心墩轴压比为0.1，在不同剪跨比、配筋率时，空心墩位移延性随纵筋强度变化情况见图13。由图13可以看出：剪跨比、纵筋配筋率不变时，空心墩极限变形能力随着纵筋强度的提高而减小，同时图中各线基本平行，说明由于纵筋强度的提高，空心墩位移延性的下降变化率不受剪跨比与配筋率的影响。

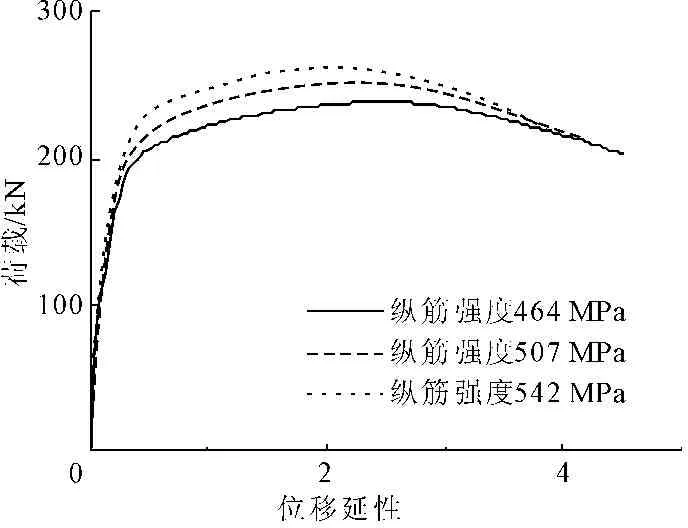
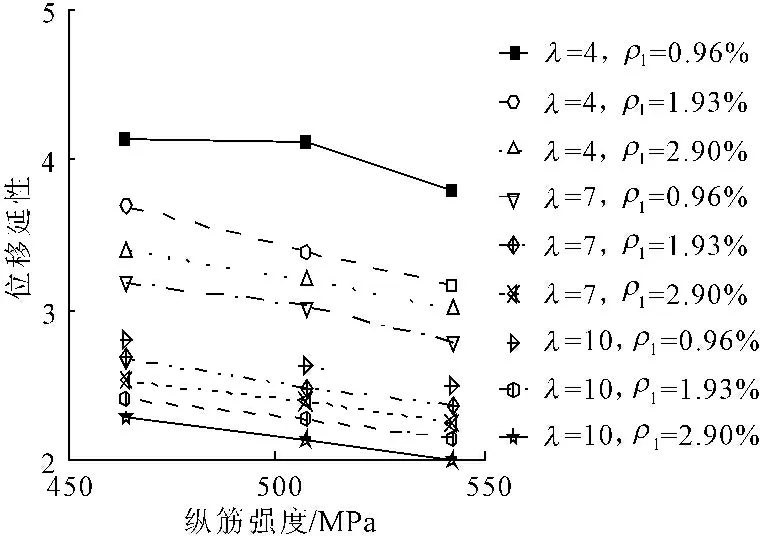
图12 剪跨比、轴压比、配筋率相同，不同纵筋强度骨架曲线

图13轴压比不同，剪跨比和配筋率相同，不同纵筋强度对矩形空心墩延性变形性能影响

5 结 论

本文通过建立钢筋混凝土空心墩纤维有限元模型[13]，对空心墩延性变形能力进行参数分析，分别讨论纵筋配筋率、壁厚、混凝土强度、轴压比等因素对空心墩延性影响[12]。现总结如下：

(1) 当轴压比、剪跨比一定时，延性变化率不受轴压比与剪跨比不同的影响，随着纵筋配筋率的提高，空心墩的承载力提高，延性能力却降低。

(2) 当轴压比、剪跨比一定时，空心墩壁厚的提高对空心墩的承载力与延性变形能力影响不大。

(3) 当剪跨比、配筋率一定时，空心墩的承载力随着轴压比的提高而提高，延性变形能力随轴压比率提高而降低。

(4) 当剪跨比、配筋率一定时，空心墩的承载力随着纵筋强度的提高而提高，延性变形能力随混凝土强度的提高而减小。

综上所述，尽管提高配筋率、轴压比及增加纵筋强度能有效的提高空心墩柱的承载能力，但随之带来的是降低空心墩柱延性能力的负面影响；但提高配箍率、降低剪跨比却能在提高承载力的同时，提高空心墩柱的延性能力。