一种北斗定向系统的周跳检测及修复方法
2019-01-05侯岩柯
董 惠,侯岩柯,王 纯
(西安建筑科技大学 信息与控制工程学院,陕西 西安 710055)
随着北斗卫星导航系统在军事和民用领域应用越来越广泛,对北斗在静态和动态条件下的快速高精度定向技术的研究成了北斗领域的重要方向。载波相位观测量是定向算法中的重要数据,要实现高精度定向必须保证载波相位观测量无周跳[1-2]。
目前,周跳检测及修复方法的理论研究主要有电离层残差法,载体相位变化率法和TurboEdit算法等。电离层残差法只能检测小范围周跳[3];载体相位变化率法性能不稳定,当载体速度变化较快时,载体相位变化率法的精度较差[4];TurboEdit算法不能检测出两个频率上发生相同周跳的情况[5]。北斗卫星导航系统使用很多载体,有相当一部分载体是动态的,如舰船和车辆。寻找一种对动态载体能有效进行周跳检测及修复的方法具有较大应用价值。
1 基于电离层残差法的周跳检测及修复方法
1.1 基本原理
电离层残差法是一种基于不同历元间电离层残差变化的周跳检测及修复方法[6]。在忽略测量噪声等影响的前提下,同一历元的双频载波相位测量之差为
φ(t)=λ1φ1(t)-λ2(t)φ2(t)=
(1)
式中:λ1,λ2分别为B1,B3频点对应的波长;φ1(t),φ2(t)分别为B1,B3频点对应的载波相位观测量;N1,N2分别为B1,B3频点对应的载波整周数;A(t)为电离层效应引起的距离偏差系数;f1,f2分别为B1,B3频点对应的载波频率。
将式(1)两边同时除以λ1,并化简得出不同两历元间电离层残差的变化量[7]:
(2)
式中:ΔN1,ΔN2分别为B1,B3频点对应的的周跳;ΔI(t)为t历元的电离层延时;无周跳时Δφ的变化值很小,如果Δφ值出现突变,则说明B1或者B3的载波相位测量值可能存在周跳。
如果|Δφ|>0.23,则t+1历元存在周跳。方程中ΔN1和ΔN2为未知数,Δφ为已知数,所以存在方程解多值性问题;如果|Δφ|<0.23,可能存在部分B1和B3非零周跳组合使得Δφ等于零或者很接近零,造成电离层残差法不能有效检测出周跳。不同(ΔN1,ΔN2)组合及其对应的Δφ值见表1。

表1 不同(ΔN1,ΔN2)对应的Δφ值
由表1可以看出,不同(ΔN1,ΔN2)组合对应的Δφ值很接近,造成方程多解。也可能存在某些特定(ΔN1,ΔN2)组合使Δφ值接近零,造成不能有效探测周跳。
1.2 实验结果
2017-05-05在某大厦顶楼用BD接收机采集观测数据,取前100个观测历元,数据采样率为1 Hz。以卫星PRN15-06为例进行算法验证,无周跳时卫星PRN06载波整周数为15 718,卫星PRN15载波整周数为9 068。在第21历元加入周跳组合(3,2),第35历元加入周跳组合(-3,2),第56历元加入周跳组合(5,4),第78历元加入周跳组合(2,5)。表2为PRN15-06基于电离层残差法的周跳检测及修复结果。

表2 PRN15-06基于电离层残差法的整周模糊度周跳检测及修复后结果
1.3 分析与讨论
由表(2)得出,在不借助其他算法的前提下,电离层残差法没有检测出第56历元的周跳,这是因为该历元B1和B3非零周跳组合(5,4)使得Δφ值很接近零,造成电离层残差法不能有效检测出周跳;第21历元、第35历元和第78历元的非零周跳组合使Δφ值大于0.23,电离层残差法能够检测出周跳。该结果与表1计算得到的结论一致,由此可见,电离层残差法对较大的周跳检测,一般超过5周时,有检测不出周跳的情况出现。
2 联合载波相位变化率和冗余双差观测量的周跳检测及修复方法
当载体处于静态时,卫星与接收机距离很大,认为卫星绕地球做匀速转动[8]。本文提出一种联合载波相位变化率和冗余双差观测量的方法,该方法弥补电离层残差法不能检测较大的周跳以及载波相位变化率易受载体速度变化影响的缺陷,对动态载体有效进行周跳检测及修复。
2.1 基本原理
设接收机在相邻的三个时刻k-2,k-1,k的双差载波相位观测值分别为φk-2,φk-1,φk,并且k-2,k-1两个时刻的双差载波相位观测量没有发生周跳,则k时刻的载波相位估计值
(3)

(4)
如果k时刻该双差观测值无周跳,则ΔNk很小,如果k时刻该双差观测值有周跳,则ΔNk大于1周。周跳量
ΔN=round(ΔNk).
(5)
其中,round(ΔNk)表示对ΔNk取整数。周跳数值为整数,当ΔN和ΔNk之差小于某一阈值ε(一般取0.3)时,即认为有周跳。
如果ΔN和ΔNk之差小于ε,如果在整周模糊度解出的情况下,则用ΔN修正相应的模糊度;如果在整周模糊度未解出的情况下,则用ΔN修正相应的状态变量。如果ΔN和ΔNk之差大于ε,认为载体的速度变化失去了应有的精度。


(6)

整周模糊度正确解算后,如果无周跳现象,则整周模糊度N不变[9-10]。对式(7)通过最小二乘法得到基线向量和基线长度:
(7)
(8)
基线长度作为常量,精确测出记为l0。如果某几颗卫星有周跳现象,则其相应的整周模糊度Ni发生变化。将计算出的基线长度与事先精确测出的基线长度进行比较,可以检测出发生周跳的载波相位观测量,再接着利用冗余双差观测量确定发生周跳的载波相位观测量的具体位置。
将式(6)用矩阵形式:
(9)
其中,In-1为(n-1)维单位矩阵。
展开
(10)
H12=λI3;H23=λIn-4;N基=[N1,N2,N3]T;N从=[N4,…,Nn-1]T;C1=[DD1(t),DD2(t),DD3(t)]T;C2=[DD4(t),…,DDn-1(t)]T;
展开
(11)
(12)

(13)
N1,N2,N3双差整周模糊度无周跳,则计算出的基线长度l(t)应该在基线测量长度值附近,设定一个阈值α,如果计算出的基线长度l(t)与基线测量长度值l0(t)的差值的绝对值不大于阈值α,即认为双差整周模糊度无周跳。计算剩余整周模糊度,替换原来的整周模糊度。
计算基线长度l(t)与基线测量长度值l0(t)的差值大于阈值α,必须重新选择三个双差模糊度,按照上述方法由这三个双差模糊度重新计算基线向量及基线长度,如果还有周跳,则继续舍弃,直到无周跳为止。
搜索全部的模糊度组合后,没有发生周跳现象,则基星可能有周跳。必须更换基星,重复上述步骤,重新搜索整周模糊度。
2.2 算法验证
2017-05-20在某地用BD接收机采集观测数据,取前100个观测历元,数据采样率为1 Hz,用卷尺测量出两个天线之间的距离为3.17 m。实验过程中安有天线的车体行驶一段距离,附近建筑物等的遮挡导致双差载波相位出现周跳。以卫星PRN15-05为例进行算法验证,设l(t)-l0=Δl,表示通过计算得出的基线长度l(t)和事先精确测出的基线长度l0的差值,设|Δl|=β。无周跳和有周跳时的基线长度误差分别如图1和图2所示。
根据图1和图2分析,在无周跳情况下,根据双差载波相位观测量计算的β小于0.01,当有周跳情况下,根据双差载波相位观测量计算的β大于0.01,故阈值α可取0.01。用MATLAB对算法进行仿真,仿真结果见表3。
2.3 分析与讨论
由表3看出,出现周跳的具体历元被确定,分别为第5、第20、第56,和第72历元,修复后β绝对值明显小于0.01,该算法不仅可以确定出现周跳的具体历元,而且可以有效修复周跳,取得较好效果。

表3 基线长度误差检测及修复结果

图1 PRN15-05无周跳时基线长度误差Δl
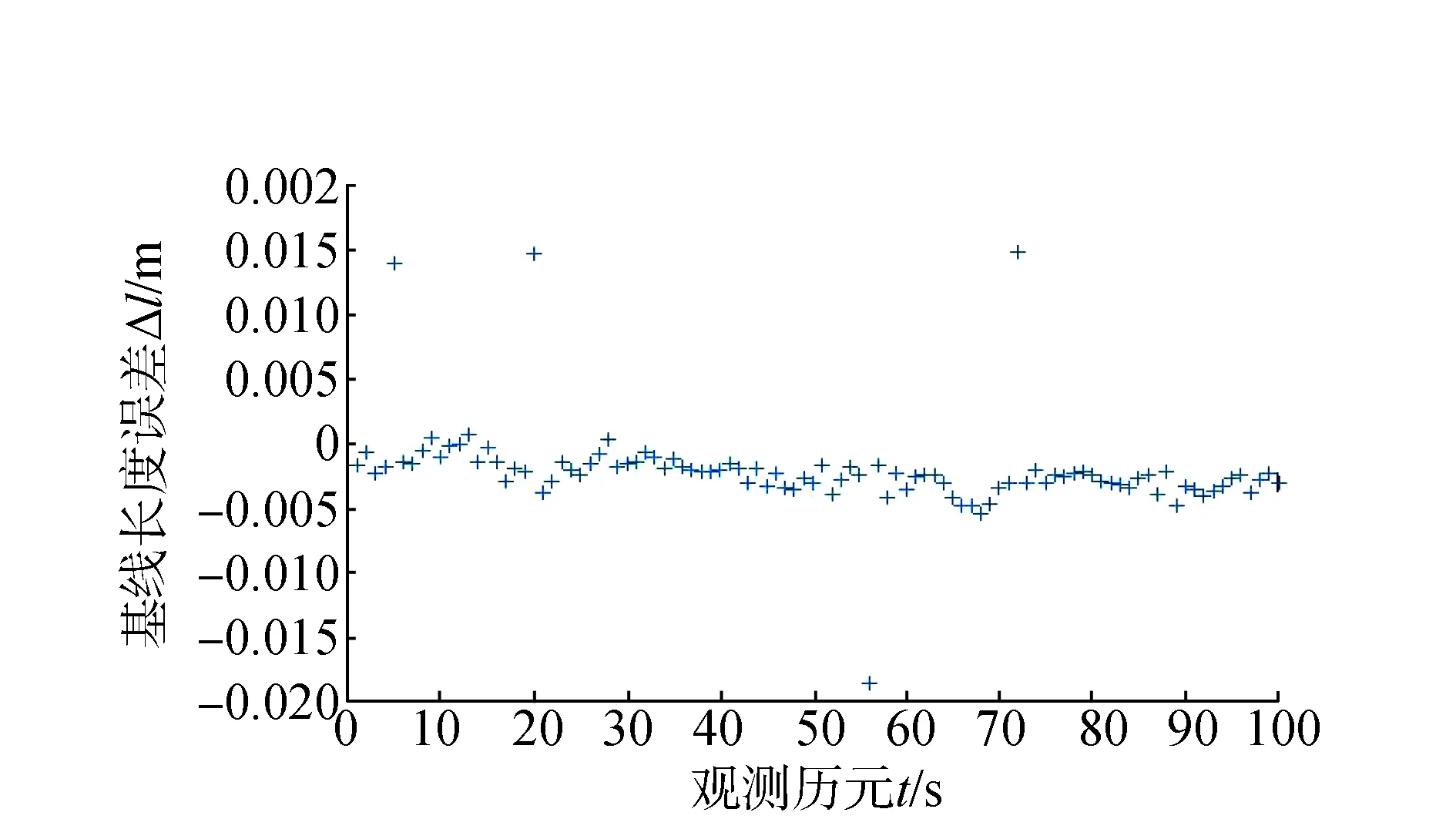
图2 PRN15-05有周跳时基线长度误差Δl
3 结 论
通过仿真结果进行分析,联合载波相位变化率和冗余双差观测量的方法,可以有效地对载体在动态情况下进行双差测量数据的周跳检测及修复,弥补了电离层残差法对较大周跳检测不出的缺陷。该算法易于编程实现,性能较稳定,可以满足载体在动态情况下,快速进行周跳检测及修复的要求,在车载定向和舰载定向等方面具有较强应用价值。
