多因素下开洞口煤仓风致积雪CFD模拟及拟合研究*

殷志祥，姜昕彤，崔翰博

(辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

0 引言

随着大跨度建筑的跨度越来越大，由于屋面积雪分布不均匀且局部雪压过大，风雪运动下结构屋面发生损毁事故增多[1-4]。我国《建筑结构荷载规范》(GB 50009-2012)分别对拱形屋面和大跨度屋面(跨度>100 m)的积雪分布系数做出规定，但规定较为简单，并不适用于开口煤仓的球壳屋盖，且在风雪共同作用下此类开口结构表面的积雪运动变化将更为复杂。因此，寻找适合风雪作用下开洞口煤仓球壳屋盖的积雪分布系数十分必要。

Murakami等[5]分别采用k-ε湍流模型和大涡模型(LES)对立方块周围的湍流分布情况进行数值模拟，并与风洞试验数据对比，发现 LES 模拟结果较为准确； Uematsu等[6]对防雪栏、风穴和小山3种模型模拟时考虑了风致雪漂的跃移和悬移运动，得到结果更接近实地观测； Beyers等[7]在对立方体模拟时细化影响因素，精确得到风雪作用下雪颗粒运动轨迹；周暄毅等[8]模拟计算了北京南站屋盖表面的积雪不均匀分布情况；孙芳锦等[9]模拟研究风向角对膜结构表面积雪漂移运动的影响，得到膜结构表面不均匀雪压分布情况；孙晓颖等[10]对比不同湍流模型下防雪栏周围风致雪漂移运动，得出k-kl-ω模型对风雪运动模拟较为准确；李跃等[11]研究矢跨比和风速对屋面雪压的影响，并求得近似公式。以上研究都以具体模型展开分析，没有适合此类开口结构的风雪研究。本文以开洞口圆形煤仓为模型，研究风雪共同作用下屋盖不均匀雪压分布，根据所得模拟结果推导出此类开口结构屋面积雪值公式，可直接应用于此后煤仓工程设计中，对今后准确预测此类开洞口结构表面雪压分布有一定的参考价值。

1 风致积雪CFD理论

1.1 空气相及雪相的控制方程

采用Reynolds平均法，风可近似为不可压缩性粘性流体，质量守恒方程及动量守恒方程[12]分别为：

(1)

(2)

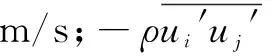
(3)

式中：ρs为积雪密度，kg/m3；f为单位体积里雪相所占组分；uj为风速矢量；μt为空气相湍流粘性系数，此系数代表空气相对雪相的影响程度；uR，j为雪相对空气的运动速度，m/s，取0.3[13]。

1.2 雪的侵蚀和沉积

摩擦速度u*(风速)是体现屋盖积雪是否发生侵蚀或沉积的决定性因素。u*的表达式为：

u*=u(z)K/ln(z/zs)

(4)

式中：u(z)为近壁面的风速，m/s；K为Karman常数，取0.4；z为积雪面到近壁的第一格栅中心高度，m；zs为积雪面粗糙度，m，取0.000 5[9]。屋盖表面积雪发生侵蚀时摩擦速度u*大于阈值速度u*t(0.20 m/s[8])，沉积时摩擦速度小于阈值速度。侵蚀量和沉积量[7]分别如式(5)～(6)所示：

(5)

(6)

式中：Aero为比例常数，取7.0×10-4；C为单位体积内雪的质量，kg，C=fρs其中，f为雪的体积分数，ρs为积雪密度，kg/m3；wf为降雪速度，m/s。

2 开洞口煤仓风致积雪CFD模拟

2.1 计算模型与网格划分

本文以某电厂圆形煤仓为工程背景，模型如图1所示，煤仓筒仓高度H为18 m[14]，煤仓帽顶直径d为20 m，高度h为2 m，煤仓跨度D分别设置为110 m和50 m，球壳屋面上正方形洞口模拟栈桥洞口。110 m跨度煤仓洞口尺寸为4 m×4 m[14]，50 m跨度煤仓洞口尺寸为2 m×2 m，门洞尺寸为4.5 m×4.5 m[15]。

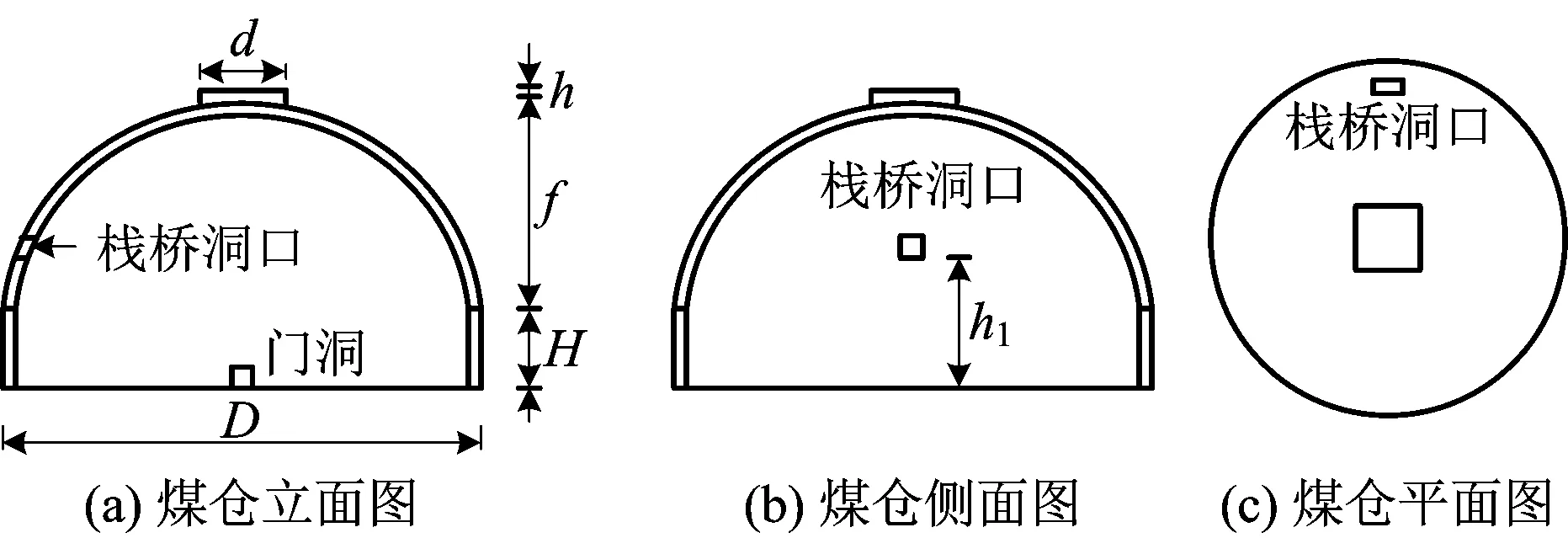
图1 开洞口煤仓模型Fig.1 Opening round coal bunker model diagram

110 m跨度煤仓计算流域为1 000 m×500 m×300 m，50 m跨度煤仓计算流域为600 m×350 m×270 m，满足阻塞率要求。混合网格划分模型，非结构化网格划分建筑物，结构化网格划分外部区域。最小网格尺寸0.5 m，网格总数约90～150万个，近壁面网格划分如图2所示。

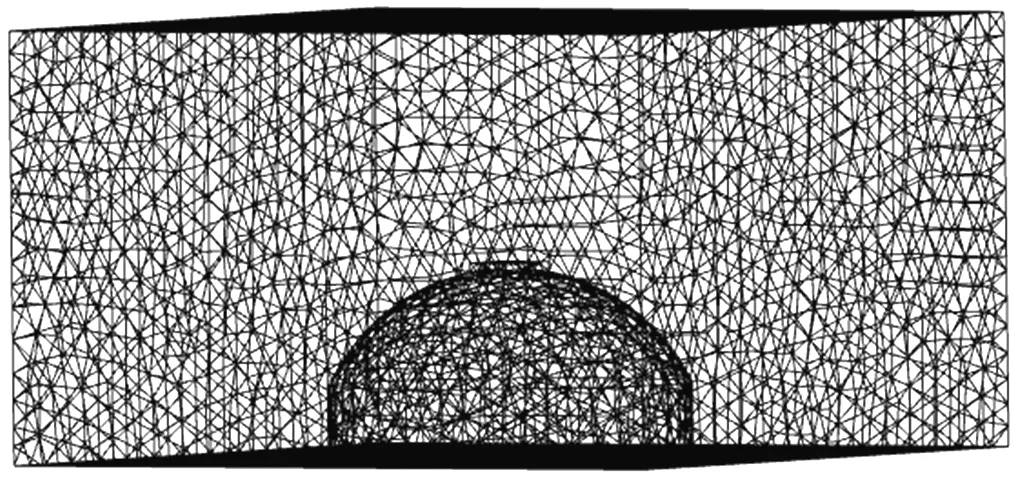
图2 近壁面网格划分Fig.2 Near wall meshing

2.2 边界条件与求解方法

入流面空气相采用速度入口边界条件，风速u(z)为：

u(z)=ub(z/zb)α

(7)

式中：zb为标准参考高度，m，取10；ub为zb对应的平均风速，m/s；z为任一高度，m；α为地面粗糙度指数，取0.15[16]。湍流动能k及湍流耗散率ε为：

k=1.5(u(z)·I)2，ε=0.090.75·k1.5/l

(8)

式中：I为湍流强度；l为湍流积分尺度，m，I和l分别为：

(9)

按日本规范取II类地貌，zb取5m；zG取350 m。

(10)

入口处雪相边界条件为：

(11)

式中：μp为雪相运动速度，m/s；g为重力加速度，m/s2；hs为跃移层和悬移层临界高度，m，为简化计算取为0.5。

出流面为完全发展出流边界条件，模型表面与地面为无滑移的壁面条件，流域上部和两侧为自由滑移避免条件。将空气和雪颗粒之间关系假设为单项耦合，采用Euler-Euler方法，认为空气相和雪相都是连续相，选择计算量小且计算稳定性较好的Mixture多相流模型，采用可实现k-ε两方程模型。

3 开洞口煤仓风致积雪参数影响分析

模拟在不同风向角(θ=0°，20°，45°)、不同积雪厚度(h=100，300，500 mm)、下跨度为50 m和110 m的开洞口圆形煤仓表面积雪分布情况，煤仓矢跨比分别设置为α=0.14，0.32，0.45的共54组工况(模型1～54)，模型编号如表1所示。

3.1 开洞口煤仓表面测点设置

在煤仓表面设4个测点，测点A和B分别位于煤仓中轴线背风面和迎风面最外侧，测点C位于垂直风向方向中轴线最外侧，即表面积雪侵蚀量最大区域，因栈桥洞口迎风侧积雪侵蚀量大于背风侧，故测点D设置在迎风侧栈桥洞口边缘，如图3所示。

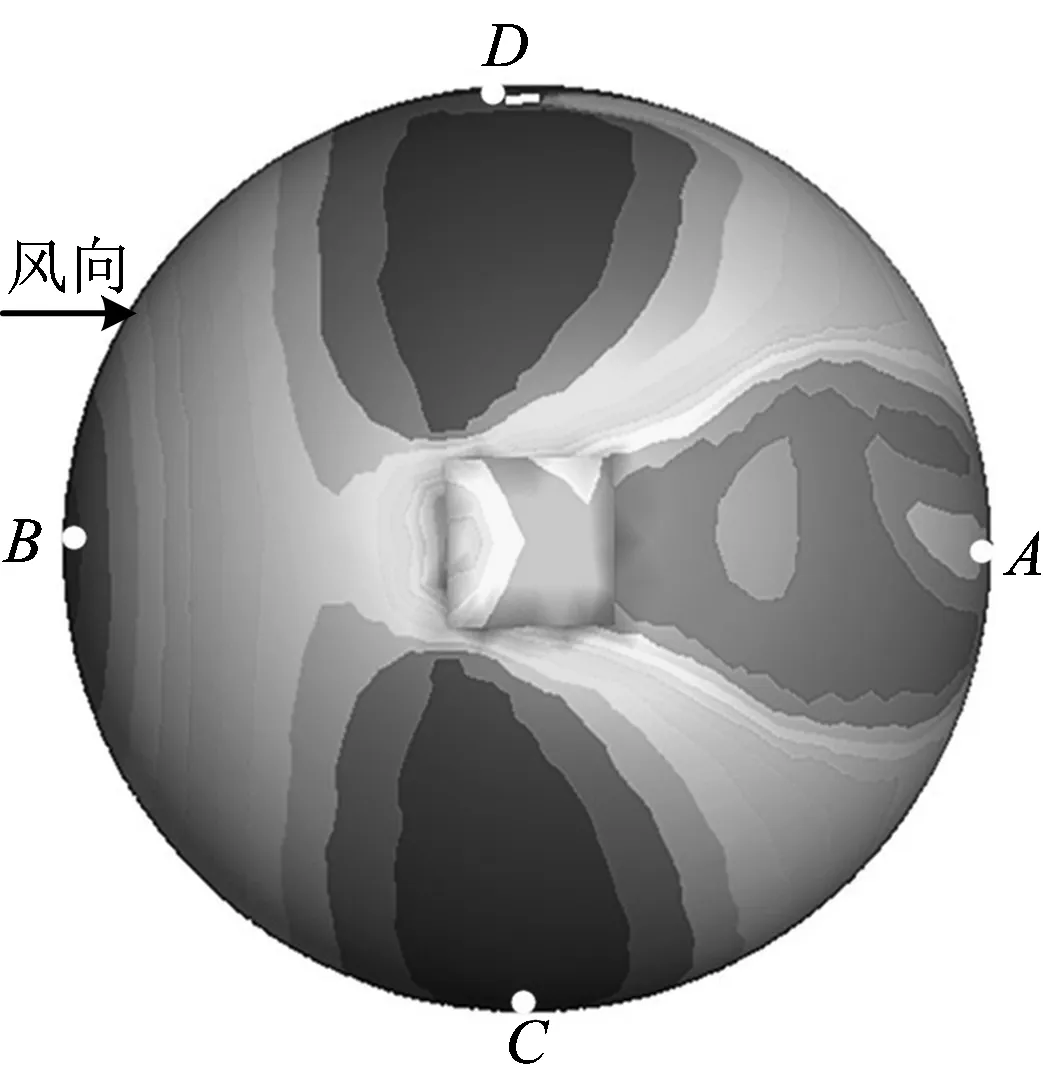
图3 测点设置Fig.3 Measuring point setting diagram

3.2 风向角对开口煤仓积雪分布的影响及测点分析

取模型9、模型18、模型27的3种工况进行分析。风向角角度定义如图4(a)所示，因篇幅有限，仅以模型9为例，得出的开口煤仓表面单位时间单位屋盖面积上的积雪侵蚀或沉积量如图4(b)所示，来流风向在图中标出，其他工况与之相同。由图4得出，煤仓表面积雪均发生侵蚀，迎风面到背风面积雪侵蚀量逐渐增大后变小，迎风面积雪侵蚀量略大于背风面，中心部位积雪侵蚀量达到最大，这与文献[11]得出结论相吻合，迎风面边缘及由于帽顶遮挡作用背风面中心部位积雪侵蚀量极小。栈桥洞口背风侧比迎风侧积雪侵蚀量小，是因为栈桥洞口可以吸收部分来流风，减小了风对表面积雪的侵蚀作用。

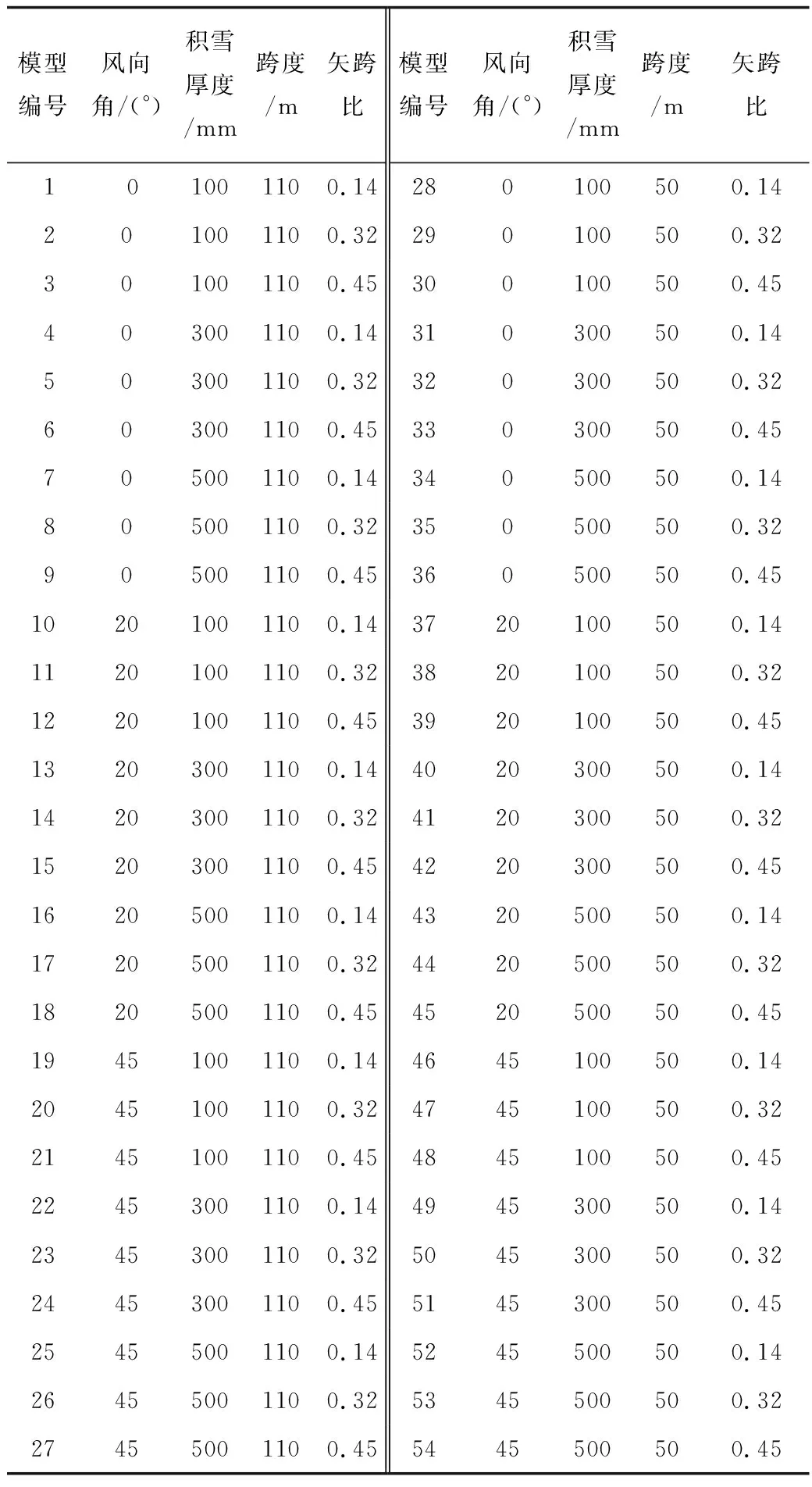
表1 模型编号与参数Table 1 Model number and parameter

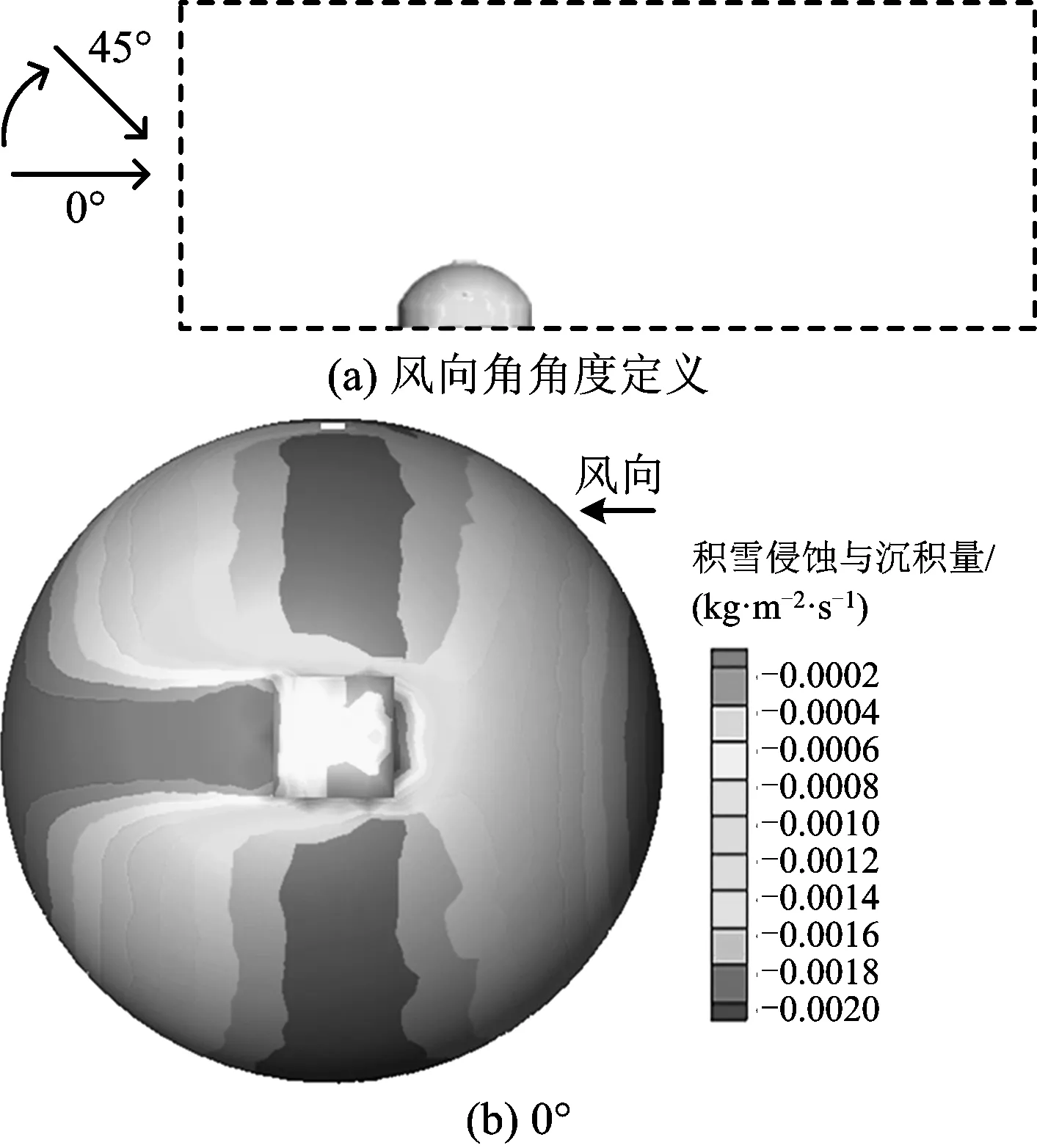
图4 不同风向角下单位时间单位面积积雪侵蚀或沉积量Fig.4 Snow erosion or sedimentation volume per unit area per unit time at different wind direction angles

图5 煤仓表面积雪量分布(模型9，18，27)Fig.5 Coal bunker surface snow volume distribution curve(model 9，18，27)

为更直观地分析风向角对开洞口煤仓的影响，汇总数据见图5，以与顺风向平行的中轴线AB为轴，每隔13.75 m设置1个测点，对测点1～ 9进行分析，测点1与B点重合，测点9与A点重合。由图5可知，随风向角增大，迎风面(测点1～ 5)积雪侵蚀量明显增加，背风面(测点5～ 9)增长幅度小。测点3和C点在45°风向角下侵蚀量比0°风向角分别增大80%和69.23%，说明风向角对开口煤仓迎风面风致积雪漂移影响尤为明显；45°风向角下D点比0°风向角增大66.67%，说明风向角对栈桥洞口附近积雪变化影响也较大，在此后煤仓设计中应重点考虑风向角对煤仓表面积雪的影响。

3.3 积雪厚度对开口煤仓积雪分布影响及测点分析

取模型30、模型33、模型36为例进行分析，煤仓表面积雪量分布曲线，如图6所示。

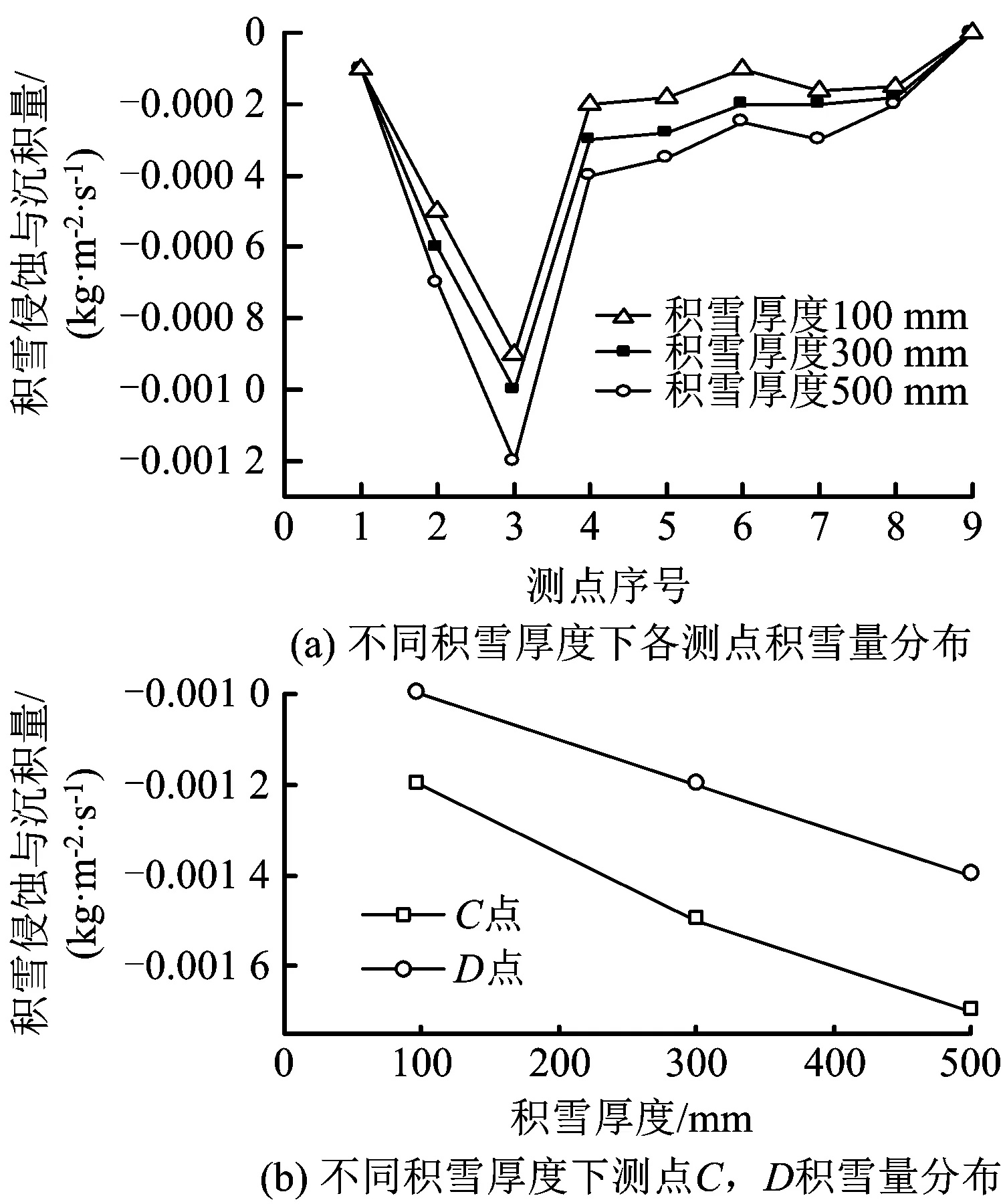
图6 煤仓表面积雪量分布(模型30，33，36)Fig.6 Coal bunker surface snow volume distribution curve(model 30，33，36)

由图6可知，3种工况煤仓表面积雪侵蚀变化规律大致相同，积雪侵蚀量随积雪厚度增大而增大。位于迎风面的测点2、测点3在500 mm积雪厚度的侵蚀量比100 mm积雪厚度分别增大28.57%和25%，背风面测点7、测点8则分别增大33.33%和50%，位于侵蚀量最大区域的C点增大29.41%，测点D则增大28.57%，由此得出积雪厚度对开洞口煤仓表面的风致积雪漂移影响也很大。

3.4 矢跨比对开口煤仓积雪分布的影响及测点分析

对110 m跨度下不同矢跨比、风向角、积雪厚度的煤仓模型进行数值模拟后发现，矢跨比为0.14时，煤仓表面积雪变化规律不同于其他情况，取模型25说明，如图7所示。由图7可知，除栈桥洞口背风侧边缘区域积雪发生侵蚀，其余区域积雪全部沉积，因0.14矢跨比的煤仓网壳坡度极小，相当于平屋盖，故积雪全部沉积在表面，栈桥洞口背风侧附近风速较大，一部分积雪发生侵蚀。

图7 单位时间单位面积积雪侵蚀或沉积量Fig.7 Snow erosion or sedimentation volume per unit area

以50 m跨度的模型28、模型29、模型30进行分析，得出煤仓表面积雪量分布曲线如图8所示。由图8可知，50 m跨度的煤仓积雪侵蚀量和栈桥洞口边缘测点D的积雪侵蚀量随矢跨比增大而增加，且风向角的改变不影响积雪变化规律。跨度为110 m，风向角0°下3种工况(模型4、模型5、模型6)，风向角20°下3种工况(模型13、模型14、模型15)模拟得出的结果如图9所示。由图9可知，110 m跨度、矢跨比为0.14的煤仓表面积雪大部分发生沉积，且积雪随风向角变化及其微弱。由图9(a)可知，0°风向角下、矢跨比为0.32的煤仓表面和测点C，D的积雪侵蚀量小于矢跨比为0.45的积雪侵蚀量；由图9(c)看出，风向角20°下此种情况正好相反。通过图8和图9得出，煤仓设计时不应仅考虑矢跨比这1种参数的影响，应把风向角对不同矢跨比的影响考虑其中。

图8 煤仓表面积雪量分布(模型28,29,30)Fig.8 Coal bunker surface snow volume distribution curve(model 28,29,30)

图9 不同工况下煤仓表面积雪量分布Fig.9 Coal bunker surface snow volume distribution curve in different conditon

4 开洞口煤仓积雪侵蚀量与沉积量公式拟合

4.1 开洞口煤仓表面积雪侵蚀量与沉积量公式拟合

由积雪量分布曲线图可以看出，煤仓中轴线背风面测点6～9的积雪值基本一致，且与测点1大致相同，故仅对迎风面测点1～6和测点C，D进行公式拟合。煤仓球壳屋面积雪呈等值线分布，故进行等值线拟合，球壳屋面上的积雪量q可以看作是中轴线测点坐标x的函数，发现测点1～6积雪值分布符合二次函数分布规律，故进行最小二乘法拟合。

(12)

式中：q(x)为煤仓屋面各点积雪量，kg·m-2·s-1；x为屋面测点坐标，m；a，b，c为待定常数。

二次函数开口大小和竖向位置分别由横向因子和竖向因子决定。积雪量q(x)是由风向角、积雪厚度和矢跨比共同决定的，为了准确地反应其比重大小引入此概念，拟合出全部工况下的二次函数，得出不同工况下的横向因子和竖向因子，横向和竖向因子会随着参数不同而发生变化，故用横向波动因子来表示横向因子的变化情况，横向波动因子如式(13)所示。

(13)

式中：Kwave-hz为横向波动因子；max(hz)为最大横向因子；min(hz)为最小横向因子；n为工况个数；hz(i)为不同工况下的横向因子。竖向波动因子同理可求。由此得出3种参数的波动因子如表2所示。修正表2各数据，如表3所示。

表2 各参数影响下煤仓屋面积雪值波动因子Table 2 The snow value fluctuation factor of coal bunker under the influence of various parameters

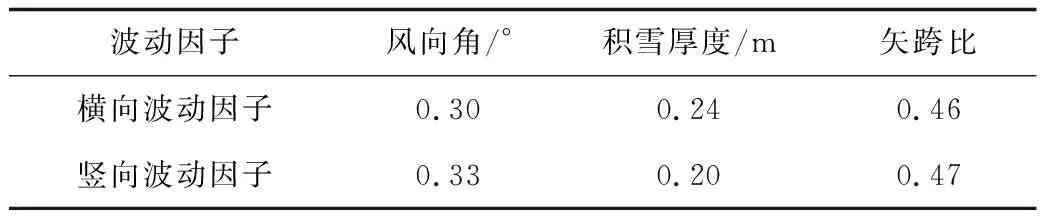
表3 修正后各参数所占比例Table 3 Proportion of parameters after modification

由表3可知，矢跨比和风向角的横向和竖向波动因子都不可忽略，经过对比分析，将测点1～6公式拟合成式(14)，各测点系数如表4所示。

(14)

式中：q1～6为各测点积雪值，kg·m-2·s-1；α为矢跨比；θ为风向角，°；x为测点坐标，m；h为积雪厚度，m；a～e为待定系数。

测点C积雪值qC拟合公式为：

qC=-9.449×10-5α2·θ-2.400×10-6θ2+0.001α-5.657×10-5h-7.590×10-4

(15)

测点D积雪值qD拟合公式为：

qD=1.569×10-4α2·θ-1.204×10-4θ- 0.003α-4.277×10-5h+0.002 (16)

4.2 公式拟合结果验证

为验证拟合公式的准确性，与文献[11]模拟结果进行对比，文献为跨度60 m、矢跨比0.22的球壳屋盖，对比结果如图10所示，因文献的球壳屋盖顶部无帽顶，且根据文献模拟结果其屋面积雪基本呈对称分布，故仅拟合半面屋盖积雪值，因其表面无洞口，故仅对式(14)和式(15)的准确性进行验证。

由图10得出，文献[11]网壳边缘到中心积雪绝对值逐渐增大，中心部位积雪绝对值最大，与本文模拟结论一致，从公式拟合结果来看，拟合规律一致，由于文献中没有考虑积雪厚度对球壳屋面的影响，故公式拟合结果与文献模拟数值有一定差别。

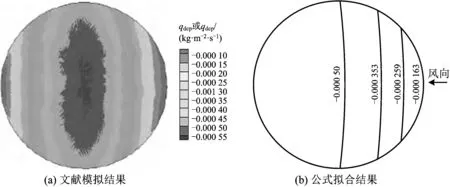
图10 文献模拟与拟合公式结果对比Fig.10 Comparison of simulation and fitting formula results

5 结论

1)开口煤仓屋面积雪量由迎风面到背风面逐渐增大然后变小，积雪侵蚀量最大位置在煤仓中心部位，随风向角和积雪厚度增大而变大，风向角对其屋盖积雪量影响不容忽视，积雪厚度对其也有一定影响；矢跨比变化下的屋盖积雪值应同时考虑风向角对其影响；煤仓栈桥洞口背风侧积雪侵蚀量小于迎风侧，在此后煤仓设计中也应注意洞口周围积雪变化情况。

2)推导出开口圆形煤仓屋面积雪量与风向角、积雪厚度、矢跨比相关公式，通过不同拟合公式可直接求出煤仓表面最不利积雪值、栈桥洞口附近积雪值及屋面其他各点积雪值。

3)拟合公式求得结果与前人模拟结果比较，发现两者屋面积雪量变化规律完全一致，最大积雪侵蚀量都在网壳中心部位，且数值相差不大，拟合效果较为良好。此公式弥补了规范中没有涉及到的开洞口圆形煤仓屋面积雪分布系数，可直接应用于工程设计中，对今后准确预测此类开洞口结构表面雪压分布具有重要的参考价值。