基于终端滑模和扰动观测的Buck型变换器复合控制技术

2019-01-05倪媛媛丁世宏

农业机械学报 2018年12期

高伟倪媛媛丁世宏

(1.江苏大学电气信息工程学院, 镇江 212013； 2.芜湖职业技术学院电气工程学院, 芜湖 241000)

0 引言

开关电源是一种电能转换装置，根据人们所需要的电压或电流，能够将电压通过不同形式的架构进行转换。对开关电源来说，其控制系统对其电压调节功能尤为重要，而控制系统主要取决于控制方法[1-2]。工程中的控制方法主要是以PID为主的线性控制。尽管PID控制易于实现，但该方法大多数情况下只能得到局部控制结果，且参数一般较难整定[3-4]。特别当扰动较大时，其控制性能往往难以达到期望要求，甚至引起系统失稳。基于此，很多学者提出了功率变换器的非线性控制方法，典型的方法有滑模控制[5]、模糊控制[6-7]、神经网络控制[8-9]以及智能控制[10-11]等。

滑模控制方法由于具有实现简单、鲁棒性强等很多其他线性控制方法所不具备的优点，近年来在功率变换器的控制设计中得到了广泛的应用[12-17]。尽管功率变换器的滑模控制已经取得了一些有意义的结果，然而现有结果存在一些共性问题。当干扰较大时，需要通过较大的控制增益才能抑制干扰的影响，而高增益会导致闭环系统的动态和稳态性能变差，甚至会引起系统状态的发散[18]。此外，由于控制器抖振与滑模控制器的增益成正比，因此高增益也加剧了滑模控制器的抖振问题。终端滑模理论上可以实现状态的有限时间收敛，在工程上具有更好的抗干扰性能。因此利用终端滑模控制技术考虑功率变换器的控制设计可以改善系统的性能。此外，若能够对干扰进行观测，并对其进行补偿，则补偿后系统的误差对系统的影响将会比干扰本身小很多。

基于此，本文提出基于终端滑模控制技术和扰动观测理论相结合的复合控制方案。

1 问题描述

Buck型变换器的基本电路拓扑如图1所示。

图1 Buck型变换器电路图Fig.1 Circuit diagram of Buck converter

图中，DC为直流电压源，VT为开关管，D为二极管，L为电感，C为电容，R为负载电阻，iL为负载电流，uc为负载电压，Vg为电源电压。

由于可控开关管存在开通和关断两种状态，对应变换器也存在两种工作模态。当开关VT开通时，功率变换状态可以描述为

(1)

当开关VT关断时，功率变换器状态可以描述为

(2)

根据以上两种情况，可以建立Buck型功率变换器的一种平均状态模型为

(3)

式中μ——开关状态

进一步，考虑扰动对系统建模的影响，式(3)可以写为

(4)

(5)

其中

(6)

(7)

由于d1(t)、ΔVg、ΔL、ΔR、ΔC都为有界变量，因此ξ1(t)和ξ2(t)也为有界的。

功率变换器在实际工况下会受到外部扰动和内部扰动的影响。外部扰动包括电磁干扰、温度、负载等因素，内部干扰主要包括元器件参数的摄动、未建模动态等。传统模型(式(3))并未考虑外部或内部扰动对状态变量的影响。基于此，考虑外部扰动和元器件参数摄动，并结合传统模型式(3)，给出了更加符合实际情况的功率变换器模型(式(5))。

控制目标：设计基于非奇异终端滑模和非线性扰动观测器的复合控制方案，使得系统在扰动情况下的输出电压能够快速跟踪上参考值。

2 复合控制器设计

2.1 非奇异终端滑模控制器

定义电压误差为

e1=uc-Vref

式中Vref——输出直流电压参考值

结合式(5)，可得系统误差状态方程为

(8)

(9)

式中D(t)——系统扰动

注意到d1(t)及其一阶导数的有界性，根据式(6)、(7)可知，存在常数dλ和dδ使得

(10)

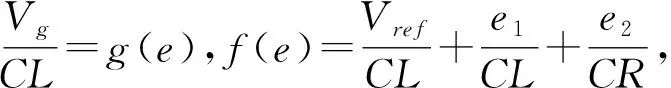
(11)

设计非奇异终端滑模面

(12)

非奇异终端滑模控制器设计为

(13)

其中K>dλ+η,η>0为任意实数，则滑动变量s可在有限时间内稳定。

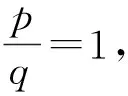
其中

1<α<2

闭环系统(11)、(13)的有限时间收敛性分析如下：

结合式(11)，对滑模面s求导可得

(14)

将控制器(13)代入式(14)可得

(15)

由式(15)可知

(16)

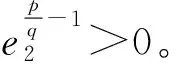
根据有限时间定理[19]可知，系统状态将会在有限时间内收敛到0。

当系统状态e2=0时，将控制器(13)代入系统(11)可得

因此当e2=0时，有

(17)

综上所述，在控制器(13)的作用下，系统(11)的状态将会在有限时间内收敛到0。

控制器(13)为非连续的，存在严重的抖振问题。此处，结合边界层方法来消除抖振，则非奇异终端滑模控制器(13)可以改写为

(18)

式中 sat(s)——饱和函数

ε——任意常数，ε>0

2.2 非线性扰动观测器设计

考虑非线性系统如下

(19)

式中x——系统状态u——系统输入

D——扰动值y——系统输出

F(x)、G1(x)、G2(x)、b(x)是与x相关的已知函数。

针对非线性系统(19)，根据扰动观测器设计理论[20]，非线性扰动观测器可设计为

(20)

式中P——非线性扰动观测器的内部状态

结合式(20)和Buck型变换器滑模控制系统模型(14)，可设计扰动观测器为

(21)

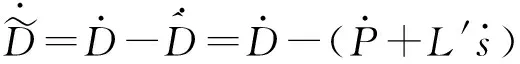
(22)

将式(18)、(21)代入式(22)可得

(23)

综上，结合非奇异终端滑模状态反馈(式(18))和扰动观测器(式(21))的复合控制器可构造为

(24)

与传统的线性滑模相比，终端滑模具有有限时间收敛的优点，且具有更强的抗干扰性能，故采用终端滑模技术进行控制设计，以使得闭环系统具有较好的标称性能。但终端滑模控制器需设计高增益对干扰进行压制，而高增益会导致很强的控制抖振。事实上，若基于扰动观测器对干扰进行估计，并进行补偿，则状态反馈控制增益可大大减小。因此，本文采用基于终端滑模的复合控制设计，弥补高增益的缺陷，减小终端滑模的抖振，进而改善系统的性能。

3 仿真

为验证文中所设计算法的可行性和有效性，在启动、突加负载和突减负载、改变输入电压3种扰动情况下，利用Matlab进行了仿真分析。Buck型变换器的参数如表1所示。

表1 Buck型变换器元件参数Tab.1 Component parameters of Buck converter

为了体现所提算法的优点，将传统的PID控制、终端滑模控制(TSM)以及复合控制(TSM+DOB)进行对比。首先，调节控制器参数使得在各控制器下系统可以得到最好的快速性能。基于此，PID参数取为Kp=8，Ki=5，Kd=0.2,而控制器(18)、(24)的参数取β=3，p=9，q=7，取边界层饱和度为ε=0.5，扰动观测器参数L′=40。如图2所示，可以看出传统的PID和终端滑模控制方法的收敛时间约为0.4 s，而复合控制的收敛时间明显较前两种短，约为0.1 s。因此，通过调节参数，复合控制器可以得到最快的收敛速度，而PID和终端滑模控制器的收敛速度在同一水平。

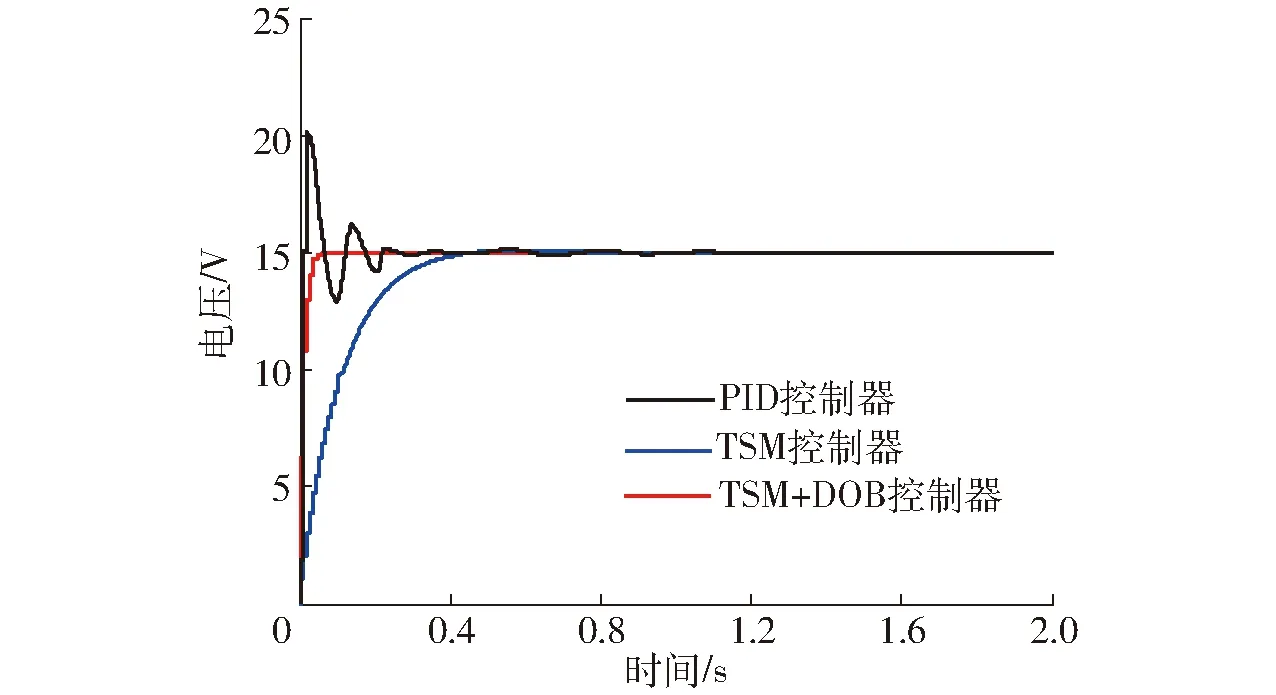
图2 无扰动时启动输出电压Fig.2 Simulated start-up waveform of output voltage in absence of disturbance

如图3所示，在1 s时将负载电阻R由25 Ω变成500 Ω，在1.5 s又将其负载恢复到25 Ω的输出电压对比。由图3可知，当输出负载突增或者突降时会引起输出电压的升高或降低，但终端滑模与扰动观测器结合的复合控制(TSM+DOB)能很快恢复到稳态值，其收敛速度明显比终端滑模(TSM)控制快。图4为负载电阻发生变化时电感电流的输出波形，可以看出复合控制能较快恢复到稳定值。由图3、4可知，加入扰动观测器后的控制器可使系统具有更好的抗干扰性能。

图3 负载电阻突变时输出电压Fig.3 Simulated step-load waveform of output voltage

图4 负载电阻突变时电感电流Fig.4 Simulated step-load waveform of inductive current

图5 输入电压突变时输出电压Fig.5 Simulated step-input-voltage waveform of output voltage

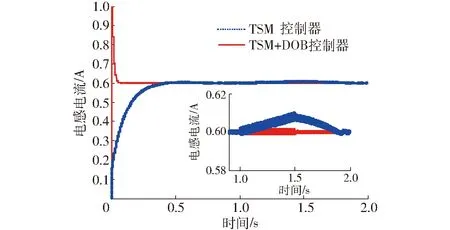
图6 输入电压突变时电感电流Fig.6 Simulated step-input-voltage waveform of inductive current

图5和图6分别为输入电压发生变化时的输出电压和电感电流的仿真结果。假设当t=1 s时，输入电压由30 V变为40 V，当t=1.5 s时，由40 V恢复到30 V，由图5可看出，当输入电压增大时会引起输出电压的变大，相比传统终端滑模控制，复合控制下的变化幅度较小且能很快收敛到期望值，由图6可以看出，在输入电压发生变化期间电感电流都会产生突变，但当输入电压恢复初始值时，复合控制的电感电流会迅速到达稳态，而传统终端滑模控制器下的电流需要一段恢复时间才能到达稳定状态，所以复合控制器控制性能较好。

综上，与传统PID控制、终端滑模控制相比，基于终端滑模和扰动观测的复合控制器具有更好的收敛和抗干扰性能。

4 实验

实验所采用的底层电路为Buck型变换器的主回路，以30 V直流电压作为输入，电压检测采用并联电阻的方法，将两组串联的电阻并联，调整其比例关系来满足DSP的电压采样范围0～3.3 V。采用日本东芝公司TLP250型驱动电路，以DSP的PWM输出作为其输入信号，同时IR2110芯片进行自举，使得PWM的输出幅值满足开关管的导通条件。图7为硬件的原理图，TLP250是一种集隔离和驱动于一体的芯片，为使芯片内的高增益线性放大器稳定，在b1和b3之间需要接一个较小的陶瓷电容以及两个限流电阻，其值取决于片内发光二极管的工作电流。

图7 硬件原理图Fig.7 Schematic diagram of hardware

实验软件部分采用DSP作为控制回路的控制芯片，由于DSP具有执行速度快，效率高，可实现多功能的实时控制等特点，被广泛应用于电力电子各个领域，图8为实验平台的总体框图。

图8 实验平台的总体框图Fig.8 Block diagram of experimental platform

选取的电器元件电感L为330 μH，电容C为1 000 pF,负载电阻R为50 Ω。终端滑模和复合控制器参数取为β=3，p=5，q=3,L′=30，PID控制参数为Kp=10，Ki=5，Kd=0.1。

当输入电压为30 V，设定的输入电压参考值为15 V。在不加扰动情况下，PID控制、终端滑模控制(TSM)以及复合控制(TSM+DOB)的对比如图9所示。

图9 3种控制器启动输出电压对比Fig.9 Experimental start-up comparisons of output voltage under PID, TSM and TSM+DOB

当负载由50 Ω突增到100 Ω时，PID控制、终端滑模控制(TSM)以及加扰动观测器的复合控制(TSM+DOB)的变负载实验输出电压对比如图10所示。

图10 3种控制器变负载输出电压对比Fig.10 Experimental step-load comparisons of output voltage under PID, TSM and TSM+DOB

在输入电压由30 V突升到35 V时，PID控制、终端滑模控制(TSM)以及加扰动观测器的复合控制(TSM+DOB)的变电压实验输出电压对比如图11所示。

图11 3种控制器变电压输出电压对比Fig.11 Experimental step-input-voltage comparisons of output voltage under PID, TSM and TSM+DOB

由图9可知，启动阶段，相对于PID控制、复合控制，终端滑模控制具有更为快速的响应性能。此外，在复合控制下输出电压很快到达期望值，收敛时间明显小于其他2种控制方案。事实上，如只考虑系统的快速性而不考虑抗干扰性，调节PID控制器参数可以使得其与终端滑模控制器具有类似的快速性能。但此时，PID的抗干扰性能较差。另外，由图10、11可知，在负载和输入电压突变的情况下，系统的输出电压都会有小幅度的变化，但复合控制时系统输出电压变化较小，说明扰动观测器对系统的扰动起到了抑制作用，提高了系统的稳定性。

在3种控制器下，输出电压稳态值的静差较大。通过多次实验表明，该静差与控制器无关，主要由底层电路引起。