导流罩长度对农用轴流风机性能的影响
2019-01-05施正香王朝元
丁 涛 赵 洋,2 施正香,3 王朝元,3
(1.中国农业大学水利与土木工程学院, 北京 100083; 2.北京市供水管网与安全节能中心, 北京 100083;3.农业农村部设施农业工程重点实验室, 北京 100083)
0 引言
轴流风机在畜禽舍和温室通风降温工程中应用广泛[1-3],其低压和大风量的特性适合农业通风的要求。农用轴流风机多以风量和能效比为性能评价指标,其性能直接影响农业设施环境调控和节能的效果。农用轴流风机通常安装在建筑墙体上,按照有无出口扩散筒可分为两类,现有研究证明出口扩散筒能够有效提升风机性能[4],若不设出口扩散筒,则会在叶轮周边安装较短的导流罩,构成半开式轴流风机。叶顶泄漏涡是该类风机叶顶区域最主要的流动特征,其产生、发展及耗散与轴流风机的气动性能密切相关[5-7]。JANG等[8-10]研究了空调室外风机叶顶区域的涡流结构,指出通过优化导流罩形状,可以控制叶顶区域的旋涡流动。导流罩长度的变化将影响叶顶区域的流场。因此,研究导流罩长度对风机性能的影响,是优化风机性能的可行途径。
王巍雄等[11]和陆志伟[12]对比了固定长度的导流罩位于叶轮不同相对轴向位置时的空调室外风机性能,发现导流罩出口边与叶片后缘齐平时风机风量最大。丁国良等[13]、王正等[14]通过模拟试验分别发现了空调室外风机和冰箱冷凝风机的导流罩轴向长度存在最佳值,使风机出口相对湍流强度最低。王嘉冰[15]研究了空调室外风机导流罩在出口位置不变时,导流罩进口位置变化对风机性能的影响,发现风机风量随导流罩轴向长度的增加而增大并逐渐趋于平稳。
目前针对轴流风机导流罩长度的研究主要集中在空调、冰箱等家电用风机领域,受限于该类风机的结构,目前尚缺乏在导流罩进口边位置固定时,其出口边位置变化对轴流风机性能影响的研究。本文通过密闭风室试验测试与数值模拟相结合的方法,研究农用轴流风机的导流罩进口边位置固定时其长度变化对风机内外特性的影响。
1 数值模拟
1.1 原型风机
本文研究对象为山东省青岛市某公司生产的镀锌铁皮风机,如图1所示。其基本参数为:叶轮直径 1 268 mm,叶片数6,叶片厚度1.2 mm,叶片材料不锈钢,外框尺寸330 mm×1 375 mm×1 375 mm,百叶窗叶片数10,百叶窗单个叶片尺寸1 305 mm×130 mm。电动机位于外框右上角(从进风侧看),电动机型号YJD90S-4,额定功率1.1 kW,电动机额定转速1 400 r/min,电动机通过带传动带动叶轮旋转,经胶带轮减速后叶轮额定转速为450 r/min。原型风机在中国农业大学农业农村部设施农业工程重点实验室进行性能测试,风机试验台如图2所示[16]。
1.2 风机模型与计算域
利用加拿大CREAFORM公司生产的Handy SCAN3D型扫描仪对原型风机叶片进行三维激光扫描,得到叶片三维模型,在建模过程中对叶片上的冲压凹槽和铆钉等结构进行了简化处理,如图3所示。

图1 原型风机实物图Fig.1 Entity of prototype fan

图2 风机试验台Fig.2 Fan test bench

图3 利用三维扫描得到的叶片模型与最终生成的风机叶轮及导流罩几何模型Fig.3 Blade model obtained by 3D scanning and finally generated geometry model of fan impeller with shroud
导流罩由一个与外框连接的竖直壁面以及一个与该壁面呈θ=85°的圆锥面组成(图4),两个面之间由r=20 mm的圆角过渡,导流罩的竖直壁面与叶顶部分的进风侧位于同一轴向位置。导流罩长-叶宽比K定义为
(1)
式中L——导流罩整体轴向长度
B——叶顶轴向宽度
原型风机L=80 mm,K=0.78。保持导流罩的竖直壁面位置以及r、θ参数不变,通过改变K的取值来研究导流罩长度对风机性能的影响。
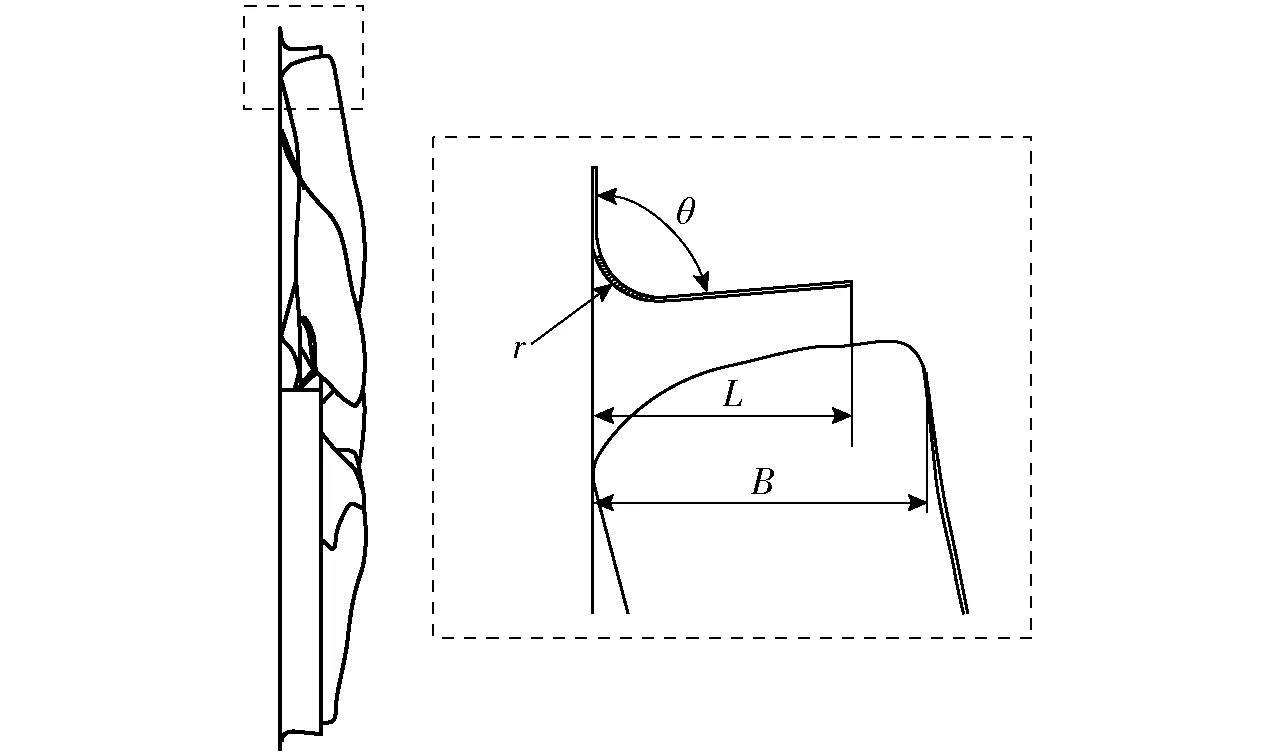
图4 导流罩结构示意图Fig.4 Schematic diagram of shroud
如图5所示,将密闭风室毕托管静压测量点的位置作为计算域进口。进口面尺寸为风室截面尺寸,即2 740 mm×2 740 mm。风机模型为通过三维扫描重构的几何模型,省略了电动机、胶带轮和支撑架等结构。风机出口接5 500 mm×5 500 mm×5 500 mm的开放域。如图6所示,风机外框被导流罩的竖直壁面分割为前后两部分,进口侧外框与风室合并造型为进口域,出口侧外框与开放域合并造型为出口域。

图5 整体计算域及边界设置Fig.5 Overall calculation domain and boundary settings
1.3 边界条件设置
如图6所示,边界条件设置如下:相对压力为1个标准大气压;进口设为压力进口,进口相对静压与性能测试时所测工况点的进口相对静压保持一致,即0、-9.8、-19.6、-29.4、-39.2、-49.0、-58.8 Pa,共7个工况点;出口设为开放边界,由于直接与大气相接,且涉及到射流卷吸,故相对开放压力设为零,选用卷吸模型;叶轮、风机外框、导流圈、百叶窗和地面等设为无滑移壁面。
1.4 网格划分
如图7所示,采用非结构网格进行网格划分,对于流动复杂的叶轮部分应适当网格加密。建立总网格数约为380万、620万和1 100万的3套网格,计算得到进口静压为-29.4 Pa时的原型风机风量分别为35 962、36 512、37 102 m3/h, 1 100万网格与620万网格相比,风量变化低于2%。综合考虑计算精度和计算资源,选择总网格数约为620万的网格划分策略,如图8所示,其中进口域网格单元数约50万,旋转域网格单元数约360万,出口域网格单元数约210万。

图6 风机计算域Fig.6 Calculation domain of fan

图7 整体网格划分Fig.7 Overall meshing

图8 叶轮网格划分(局部)Fig.8 Impeller meshing (partial)
1.5 数值计算方法
利用ANSYS CFX 15.0软件采用全隐式耦合求解技术进行稳态模拟,选用RNGk-ε湍流模型,已有研究表明该湍流模型对低压轴流风机进行性能模拟效果最佳[17],RNGk-ε湍流模型通过采用解析式计算湍动能及湍流耗散率的湍流普朗特数,代替了标准k-ε湍流模型中固定不变的湍流普朗特经验常数,提高了该湍流模型的模拟精确度;同时在湍流耗散率ε的输运方程中加入耗散能修正项Rε有利于对卡门常数的估算[18]。动量方程对流项和湍流输运方程对流项采用高阶精度格式。求解残差达到10-4量级且趋于稳定时认为计算收敛。
2 计算结果及分析
2.1 模拟结果与试验结果对比
由于在农业风机中,相比于风机的压升,风量更直接影响农业设施的通风换气效率,因此风量是用户最为关注的农用轴流风机性能指标。在农业风机领域,习惯上用能效比E表征风机的能效,表示单位耗电量所产生的风量。能效比越高,节能效果越佳,其计算公式为
(2)
式中q——风量,m3/h
p——电机输入功率,W
模拟相对误差δ为
(3)
式中Δ——模拟值与试验值的差值
T——试验值
将K=0.78的原型风机风量数值模拟结果与试验台测试结果对比,如图9所示,7个工况点的风量模拟相对误差在-4.6%~-0.7%之间,平均误差-2.77%。模拟风量与试验风量的相对误差较为稳定,两条曲线的趋势较为一致。

图9 原型风机风量模拟值与试验值对比Fig.9 Comparison of simulated and experimental values of air volume about prototype fan
由于风机传动结构紧凑,无法布置扭矩仪测量轴功率,能效比的试验值由试验风量除以电动机输入功率得到,而数值模拟中只能得到叶轮轴功率。为了使数据更具可比性,将数值模拟中的叶轮轴功率修正到电动机输入功率,其中电动机效率取GB 18613—2012规定的二级能效限定值84.1%,普通V型胶带传动效率取89%,主胶带轮的轴承效率取94%[19]。
如图10所示,7个工况点的能效比模拟相对误差在-2.5%~1.9%之间,平均误差-0.2%。模拟能效比与试验能效比的相对误差较为稳定,两条曲线的趋势较为一致。

图10 原型风机能效比模拟值与试验值对比Fig.10 Comparison of simulated and experimental values of air volume about prototype fan
上述原型风机风量、能效比的模拟值与试验值对比,两者存在较小的误差。数值模型对传动部分和叶片冲压凹槽、铆钉等结构进行了简化,并且传动部分的效率通过查询手册资料得到,这可能是误差产生的原因。总体可以认为模拟值与试验值吻合度较好,该数值模型能够反映风机的实际性能特性。后续模拟试验将以该数值模型为基础,研究导流罩长度对风机性能的影响。
2.2 导流罩长度对风机外特性的影响
在数值模拟中K取0.50、0.78、0.90、1.0、1.1、1.2、1.5、2.0共8个值。如图11所示,在不同的静压工况下,风量随导流罩长-叶宽比K的增加普遍呈现出先升高再缓慢下降并趋于平稳的变化规律。
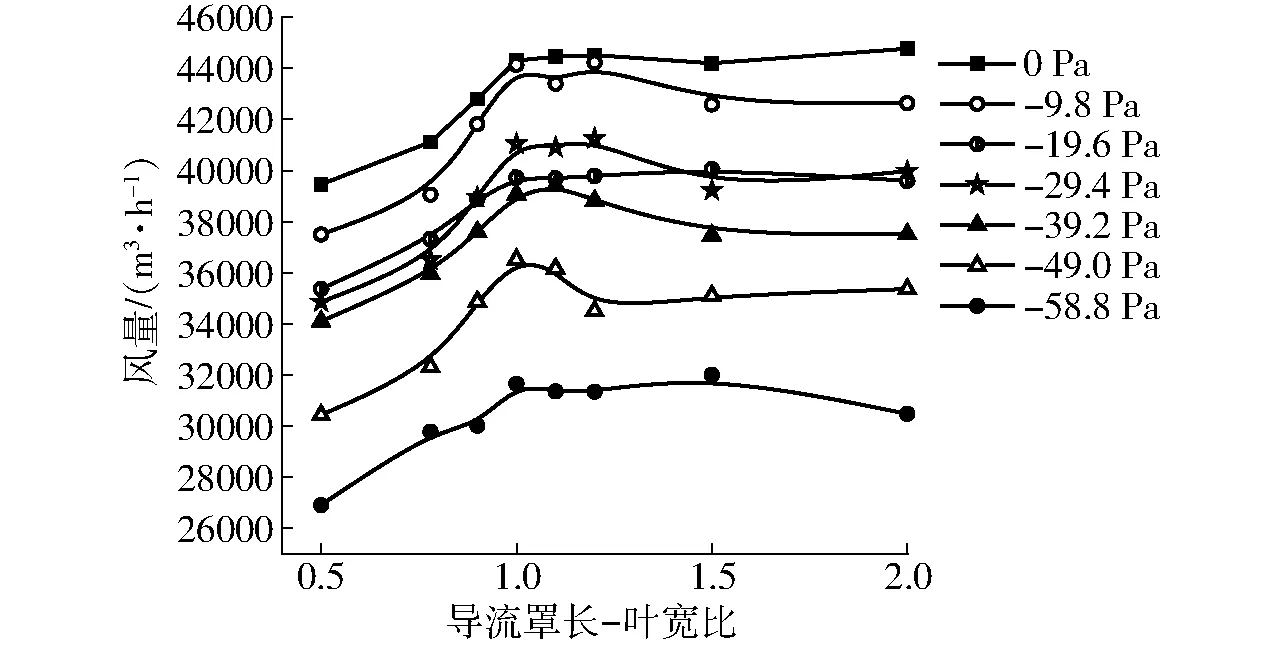
图11 不同静压时风量随K的变化曲线Fig.11 Changing curves of air volume with K when static pressures were different
为了进一步消除单个模拟值波动误差的影响,更好地观察风量随能效比的变化规律,将7个进口静压工况的风量取平均值;另外,由于-40~-20 Pa是农用轴流风机的常用工作区,因此将-19.6、-29.4、-39.2 Pa这3个进口负压工况的风量取平均值进行分析。如表1所示,随着导流罩长-叶宽比K由0.50提升到1.0,风量有较为明显的提升,在K取值1.0~1.1之间时,风量处于最高水平,在K从1.2升至2.0的过程中,风量相比最高值略有下降,并逐渐趋于平缓。K=1.0与K=0.78时相比,7个工况点平均风量提升10.1%,常用工作区3个工况点平均风量提升9.2%。

表1 不同K的平均风量Tab.1 Changes of average air volume with K m3/h

图12 不同静压时能效比随K的变化曲线Fig.12 Changing curves of energy efficiency ratio with K when static pressures were different
探究K变化对风机能效比的影响,如图12所示,在不同进口静压工况下,能效比随导流罩长-叶宽比K的增加,普遍呈现出先升高再下降的变化规律,能效比多在K=1.0或K=1.1时达到最大值。将7个静压工况取平均值,并对位于常用工作区的-19.6、-29.4、-39.2 Pa这3个工况的能效比取平均值。如表2所示,导流罩长-叶宽比K在0.50和0.78时,风机能效比处于较低水平,K由0.78提升到1.0,风机能效比有较大幅度的提升,K取值1.0~1.1之间时,能效比处于相对的最高水平,从K=1.2开始,能效比随K值的增加而呈现下降趋势。K=1.0与K=0.78时相比,7个工况点平均能效比提升10.7%,常用工作区3个工况点平均能效比提升9.6%。
2.3 导流罩长度对风机流场特性的影响
2.3.1旋转域叶顶泄漏涡的Q准则识别
为了进一步研究K的变化对风机内特性的影响,选取农用轴流风机常用工作区(-40~-20 Pa)的中间值,即进口相对静压为-29.4 Pa时的不同K值案例的内部流场对比分析。

表2 不同K的平均能效比Tab.2 Changes of average energy efficiency ratio with K m3/(h·W)
利用涡辨识方法显示数值模拟计算结果中涡流的三维结构,目前常用的涡辨识方法有多种[20],本文选用Q准则识别涡结构,相比于涡量识别方法,Q准则能够避免由壁面强剪切引起的涡结构的错误识别。
λ3+Pλ+Qλ+R=0
(4)
HUNT等[21]基于式(4)的第二变量提出Q准则,定义为
(5)

(6)
(7)
式中Ωij、Sij——旋转率张量、应变率张量
uij、uji——速度张量
Q准则反映了旋转率和应变率的关系。Q表示转动速率的ΩijΩij超过应变率SijSij的程度。在Q>0的位置,转动速率ΩijΩij占主导地位,即在该区域涡旋结构占主导地位[22]。
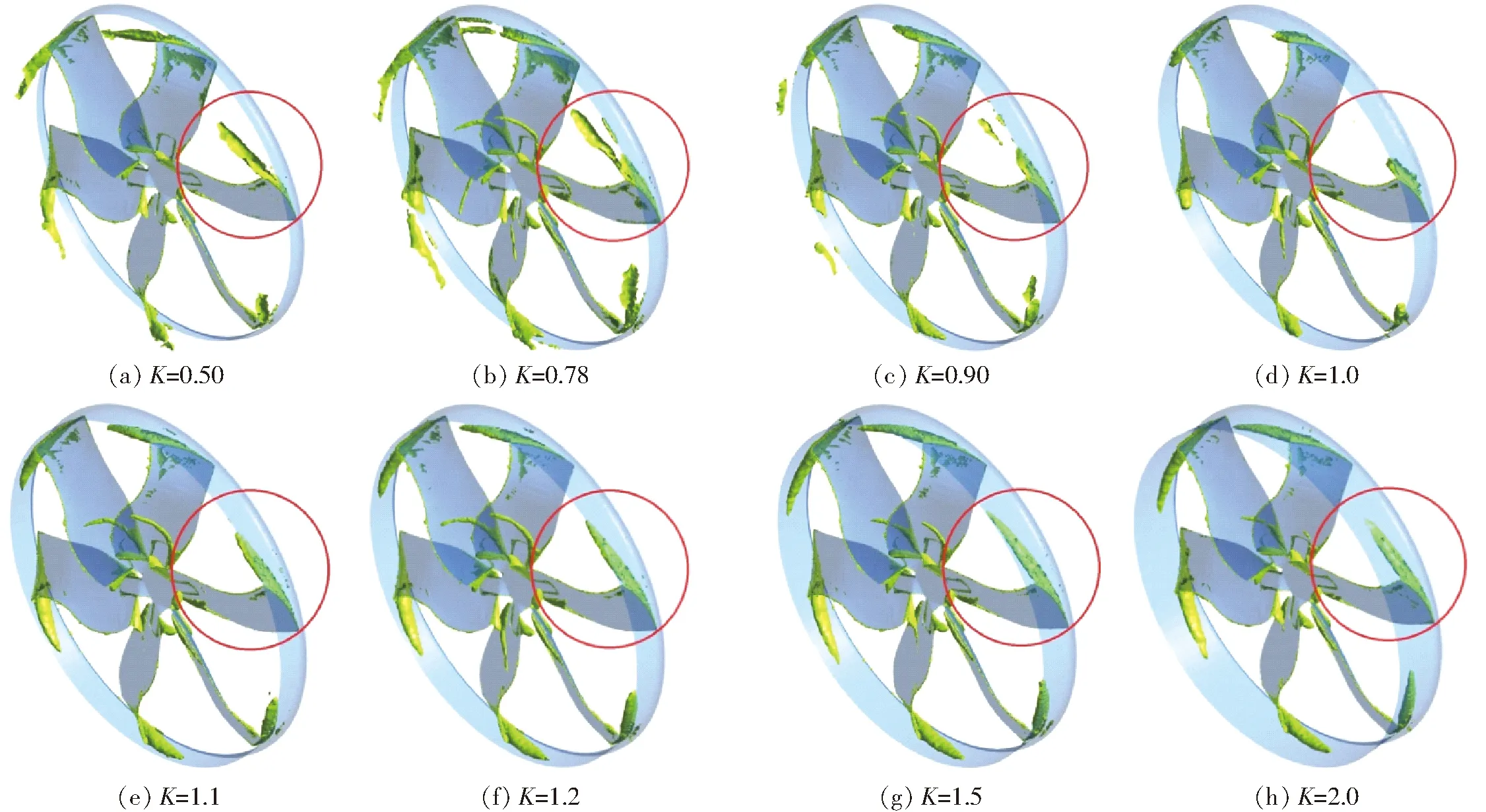
图13 风机旋转域Q准则等值面图(Q=4×104 s-2)Fig.13 Isosurface of Q criterion at fan rotating domain (Q=4×104 s-2)
如图13所示,在叶轮旋转域,如红圈中黄色Q准则等值面所示,Q准则能够识别出位于叶顶处的间隙泄漏涡。叶顶泄漏涡起始于叶顶背面前缘,并沿叶顶背面发展。K=0.50时,旋转区域的泄漏涡在叶片背面发展成一条超出导流罩出口边的不规则涡带;K=0.78时,该涡带在导流罩出口边出现断裂倾向,以导流罩出口边为界,分裂为上下游两处涡带;K=0.90时,导流罩出口边下游涡带体积明显减小;K=1.0时,导流罩出口边下游的涡带完全消失,仅剩位于叶片背面的涡带,该涡带在导流罩出口边附近停止发展,叶顶泄漏涡带的总体积在所有案例中最小;K=1.1时,叶片背面涡带长度明显增加,但未超出导流罩出口边;K=1.2、K=1.5时,随着导流罩长度的增加,涡带长度略有增加。K=2.0时,该增长趋势不再明显。
2.3.2叶顶区域流线图及轴向速度云图
为了观察更为详细的流场细节,过叶轮轴线沿竖直方向做截面,该截面接近叶顶后缘区域,图13的分析表明,该区域叶顶泄漏涡发展较为充分且K=0.78时叶顶泄漏涡在该区域发生了分裂,因此该截面的流场信息能够反映不同案例的流场特性。故取该截面的叶顶部分作对比分析(图14),截面位置及观察视角如图15所示,图14中各线条含义参见图16。

图14 叶顶位置的流线和轴向速度云图Fig.14 Clouds of streamlines and axial velocity at tip of blade

图15 图14截面位置和视角示意图Fig.15 Sketch of section position and observation direction of Fig.14
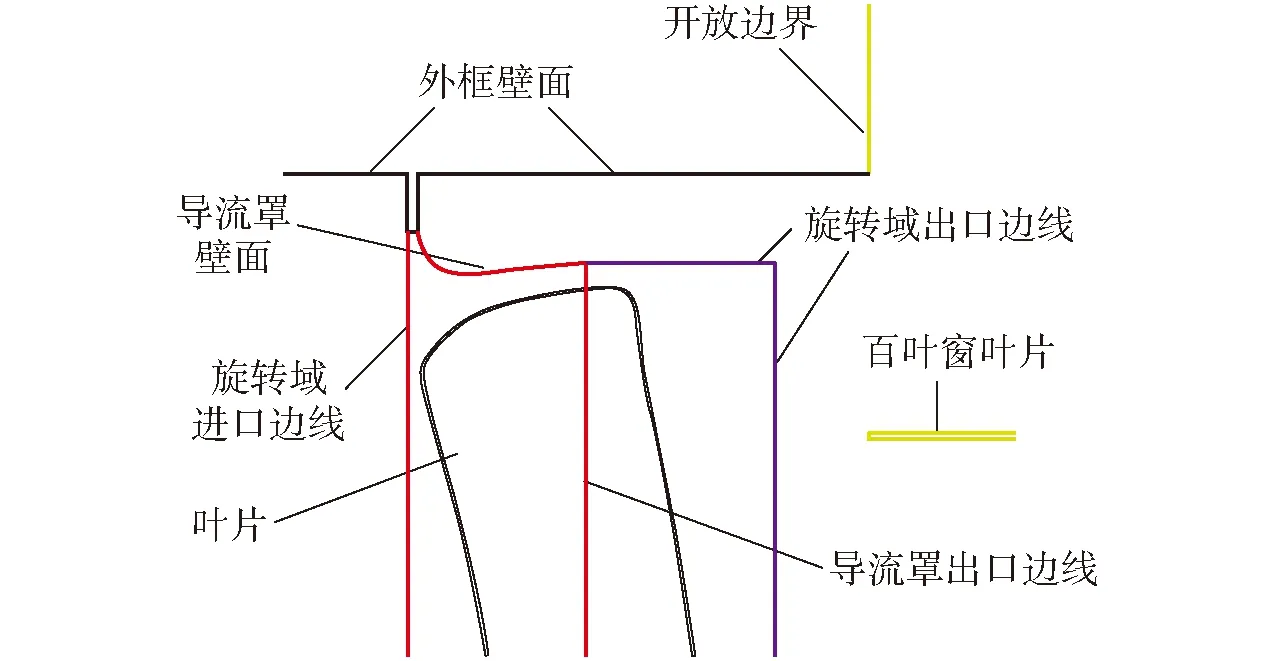
图16 图14中各线条含义Fig.16 Meaning of each line in Fig.14
如图14所示,K=0.50时,叶顶处的泄漏涡由于缺少导流罩的阻挡,发展至外框区域,形成了较大的涡旋;K=0.78时,该泄漏涡被导流罩截断为两部分,一部分成为位于叶顶与导流罩之间的叶顶涡,另一部分发展为位于外框区域的外框涡;K=0.90时,叶顶涡继续存在,但由于导流罩对从叶顶进入外框的气流进行了有效的阻隔,引导空气沿轴向流出,从而导致外框涡消失,但此时导流罩对叶顶气流的轴向引导能力不足,从叶顶流出的气流与叶轮轴线呈较大角度;K=1.0时,从叶顶流出的气流与叶轮轴线所呈角度明显减小,叶顶涡的强度在所有案例中最小,从轴向速度云图可以看出,此时叶顶涡处轴向低速区明显小于其它案例,叶顶漩涡区的阻塞效应明显减轻,导流罩有效流通面积增加,这可能是K=1.0时风机风量最大的原因之一;K=1.1时,叶顶涡较K=1.0时有所增强,从叶顶流出的气流与叶轮轴线所呈夹角与K=1.0时相比也有所增大,这种气流扩散度的增大可能是由增强的叶顶涡所导致的;K=1.2时,由于导流罩长度的增加,从叶顶流出的气流与叶轮轴线所呈夹角有所减小,说明导流罩的加长在K=1.2时开始抵消叶顶涡对扩散度的增大作用,使得出口气流的扩散度有所减小;K=1.5时,导流罩出口气流的扩散被进一步控制,叶顶涡对气流扩散度的影响基本被消除;K=2.0时,在外框区域的出口呈现出一定程度的不规则流动,这可能是由导流罩过长导致的外框出口面积减小所致。图14所反映的流场涡结构随K值的变化规律与图13所示较为一致,表明了Q准则在叶顶泄漏涡结构识别方面的有效性。
2.3.3外框涡的Q准则识别
通过对图14的分析可知,导流罩长度变化不仅影响叶顶涡的强度,对外框区域的涡强度也有较大影响。由于图14只展示了单个截面的流场信息,为了全面观察导流罩长度变化对整个外框区域涡强度的影响,图17采用与图14相同的观察方向,利用Q准则等值面图显示了整个外框区域与百叶窗附近的涡结构。将外框、导流罩和叶轮做不同程度半透明淡蓝色处理,外框用红线圈出,黄色部分为Q准则等值面。

图17 外框与百叶窗区域Q准则等值面图(Q=2×104 s-2)Fig.17 Isosurface of Q criterion at outer frame and shutter domain (Q=2×104 s-2)
如图17所示,不论K如何变化,百叶窗附近均存在不同程度的涡结构,这些涡结构将会影响降低风机有效流道面积,导致风量降低,这与现有试验研究[23]一致。K=0.50时,在外框区域呈现出大量不规则的涡结构;K=0.78时,外框区域的涡结构体积明显减小;K=0.90时,外框涡开始集中在导流罩出口边的下游,而在导流罩出口边的上游已没有明显的外框涡;从K=0.90至K=2.0,外框涡均能够被较好地控制在导流罩出口边的下游。图17显示的涡分布与图14的分析较为一致,导流罩的加长能够明显降低外框涡的强度。
3 结论
(1)导流罩的长度变化对风机外特性有明显影响,导流罩长-叶宽比K最佳值在1.0~1.1之间,此时风机的风量和能效比均处于最佳水平,导流罩过短(K<0.90)会导致风量和能效比快速下降,导流罩过长(K>1.1)并不能提升风量和能效比,反而使风量和能效比在一定程度上有所降低。K=1.0时,常用工作区平均风量和平均能效比较原型风机(K=0.78)均有10%左右的提升。
(2)通过Q准则能有效识别出叶顶泄漏涡的结构,与流线及轴向速度云图所反映的流场特征具有较好的一致性。
(3)导流罩过短(K=0.50)时,叶顶泄漏涡将从叶顶处无阻碍地发展至风机外框区域,引起外框区域涡结构的增多。导流罩加长过程中(K=0.78),叶顶泄漏涡被导流罩分裂成存在于叶顶以及外框区域的两部分,即叶顶涡与外框涡。导流罩加长至K≥0.90后,叶顶涡将经历衰减和再发展的过程,同时外框涡强度有所降低,且其能够被较好地控制在导流罩出口边下游。导流罩长-叶宽比K取值1.0时叶顶泄漏涡的强度最低,叶顶泄漏涡强度的降低能增大风机导流罩有效流通面积,有利于风量的提升。K≥1.1之后,外框涡虽已得到有效控制,但是叶顶涡强度增大,并随着导流罩的加长而在叶片出口侧下游贴合着导流罩内壁继续发展。
