Ar+轰击SrTiO3表面缺陷的模拟计算方法研究
2019-01-04
(电子科技大学电子薄膜与集成器件国家重点实验室,四川成都 611731)
由于计算机模拟实验方法相对成本低、易操作、变化范围大,所以计算机模拟得到广泛运用。计算机模拟离子注入主要包括分子动力学和蒙特卡罗(Monte Carlo)方法。
蒙特卡罗方法,又称为随机抽样或统计实验方法。它的基本思想就是通过实验的方法得到某件事情出现的频率或者这个随机变量的平均值,从而来求得这个问题的解。由于传统的经验方法无法逼近真实的物理过程,很难从中获取满意的结果。而蒙特卡罗方法能够真实地模拟实际物理过程,所以其得到的结果与实际非常符合。常用的蒙特卡罗程序有MORSE、EGS、SRIM等。SRIM作为一套开源的离子注入模拟软件,是目前模拟离子注入运用最广泛的。SRIM(The Stopping and Range of Ions in Matter)是一组计算离子在物质中能量损失和分布的程序,利用量子力学处理离子-原子碰撞,通过使用统计算法,计算所有离子经过的碰撞,然后平均碰撞结果,从而使计算变得非常有效[1-2]。本文采用SRIM程序模拟Ar+轰击SrTiO3。
钛酸锶(SrTiO3简称STO)是典型的钙钛矿型晶体,由于其原子致密度低、易于相变,相比硅、锗等典型的半导体具有更加丰富的晶体结构和物理性质。通过掺杂、薄膜化等方法,可以对其化学组分改造从而改变其物理性能,获得指定性能的STO材料。因此,STO可以通过离子注入的办法使其成为半导体材料、超导材料、磁性材料等,使其备受人们的青睐[3-4]。
STO单晶本身是一种绝缘体,但在Ar+轰击处理以后能在其表面得到具有高迁移率、高电导导电层,由于氧比锶、钛都要轻,并且氧的阈值位移能量比锶、钛都要低,所以在Ar+轰击时氧更容易被击出原有位置且扩散更快,所以会有大量的氧原子被刻蚀,从而形成氧空位[5-8]。所以普遍认为导电层与氧空位浓度密切相关,Reagor和Butko用Ar+轰击STO也在其表面获得了高电导、高迁移率的导电层[9-13],提出了氧空位导电机制理论。
目前,国内外对STO晶体表面导电层厚度的测试都是通过实验的方式。用原子力显微镜测试Ar+轰击STO表面导电层,使其表面形成台阶,再用Gwyddion软件分析台阶高度,从而获取导电层厚度。
而本文采用模拟的方法来获取Ar+注入STO的氧空位浓度。由于SRIM程序不能考虑到时间,所以在模拟的过程中不能真实体现出实际实验过程中的刻蚀效应。所以本文采用了将时间切分的方法,以单位时间为基准进行模拟,每个单位时间时则考虑前一个单位时间的刻蚀效应,这样不断进行迭代计算,最终得出一条与时间相关的曲线。
1 计算方法
首先,模拟参数为:Ar+的注入能量为300 eV,STO 的密度为5.113 g/cm3。 Thomas等[14-15]利用计算机模拟技术,采用原子间作用力的经验电荷模型和密度泛函理论定量计算了STO(空位和间隙)简单缺陷的模式和能量。他们用分子动力学模拟的方法计算了低能离子注入时STO中Sr、Ti、O的阈值位移能量,在引入主要撞击原子(PKA)之后,对每个PKA的能量和方向进行了模拟,最终得出了不同方向的阈值位移能量如表1所示。假设各个方向碰撞几率相同,根据加权平均值得到各个原子的阈值位移能量为氧50 eV、锶70 eV、钛140 eV。
然后利用SRIM程序模拟Ar+注入STO中,得到第一个单位时间不同原子的分布以及原子空位数。用氧原子空位数乘上注入剂量得到氧空位浓度,从而计算出非晶层厚度。同时,根据输出数据的原子溅射比例计算出刻蚀之后的STO的密度以及刻蚀掉的厚度。接着,进行下一个单位时间的模拟,此时设置两层靶材料,第一层为相应密度、厚度的被刻蚀之后的STO层,第二层为STO晶体,用SRIM程序模拟Ar+注入双层靶材料中,计算出氧空位浓度和非晶层厚度。同理,根据输出数据的原子溅射比例计算出刻蚀之后的STO的密度以及刻蚀掉的厚度。之后按照上述方法不断迭代计算,直到算出所需的非晶层厚度为止。总体流程图如图1所示。
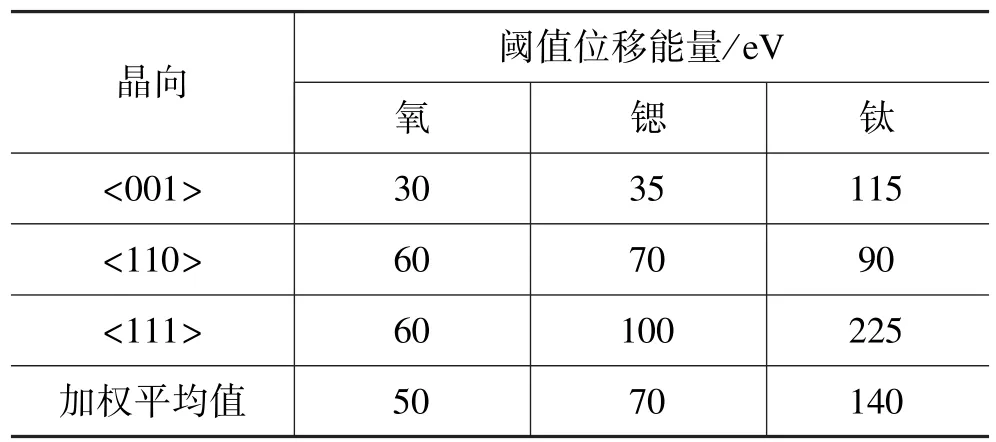
表1 氧、锶和钛原子的阈值位移能量,在300 K的SrTiO3中,不同的主要晶体方向上,用阈值缺陷形成概率为50%Tab.1 Threshold displacement energy of oxygen,strontium and titanium atoms in SrTiO3perovskite at 300 K,in various principal crystallographic directions,as de fi ned using a threshold defect formation probability of 50%
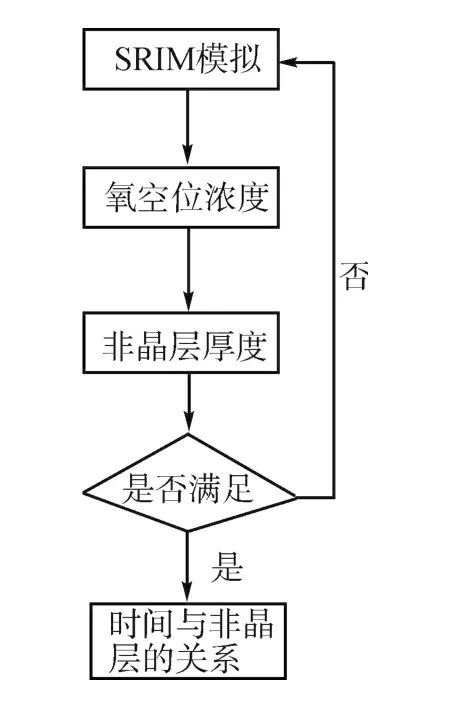
图1 模拟计算方法流程图Fig.1 Flow chart of simulation method
2 结果与讨论
先设置实验条件:Ar+的注入能量为300 eV,每秒的注入剂量为1015cm-2,以1 s为一个单位时间,氧空位浓度达到初始STO原子浓度的10%时视为该晶体被非晶化(为了方便后面的计算,数值可设置任意值,与实验需求、实验设备有关)。
图2是第一次模拟后计算出的靶材深度与氧空位浓度的关系。其中,横坐标表示距离晶体表面深度,纵坐标表示氧空位浓度。可以看到,氧空位浓度近似符合高斯分布,峰值浓度在距靶材表面0.6 nm处,氧空位峰值浓度为4.42×1021cm-3。 上文中提到氧空位浓度达到初始STO原子浓度的10%时视为该晶体被非晶化,而钛酸锶的原子浓度为1.67×1022cm-3,即氧空位浓度达到 1.67×1021cm-3视为被非晶化。交点处d1、d2之间表示氧空位浓度超过10%,这一段已经被非晶化。Xd1=0.2826 nm,Xd2=1.4544 nm,所以非晶化层厚度为1.1718 nm。同时,注入过程中存在刻蚀效应,根据溅射原子比例,计算出刻蚀深度为0.151 nm,刻蚀之后STO密度为 5.061 g/cm3。
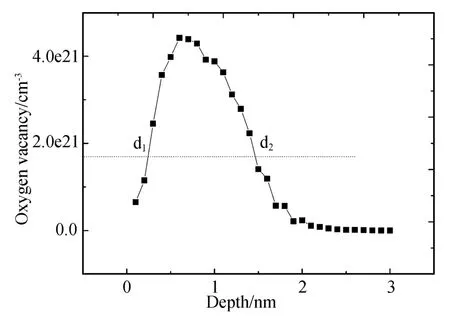
图2 第一个单位时间内氧空位浓度的分布情况Fig.2 Distribution of oxygen vacancy concentration in the first unit time
图3是靶材深度与氧空位浓度的关系。其中,横坐标表示距离晶体表面深度,纵坐标表示氧空位浓度。从左到右依次为前四次模拟计算结果。在模拟第二个单位时间时,靶材料为两层,第一层密度为 5.061 g/cm3、 厚度为 0.15 nm(上一步计算所得)的STO层,第二层依然是STO晶体。模拟的结果如图中圆形曲线所示。可以看到,氧空位浓度近似符合高斯分布,峰值浓度在距靶材料表面1 nm处,氧空位峰值浓度为4.53×1021cm-3,同样计算出非晶层厚度为 1.2925 nm,刻蚀厚度为0.159 nm,刻蚀之后 STO的密度为 4.984 g/cm3。第三次模拟结果如图中菱形曲线所示,峰值浓度在距表面1.27 nm处,氧空位峰值浓度为4.32×1021cm-3,非晶层厚度为1.3912 nm。同样,计算得到刻蚀厚度为0.148 nm,刻蚀之后STO的密度为4.896 g/cm3。第四次模拟结果如图中三角形曲线所示,峰值浓度在距表面1.4 nm处,氧空位峰值浓度为 4.47×1021cm-3,非晶层厚度为1.5113 nm。
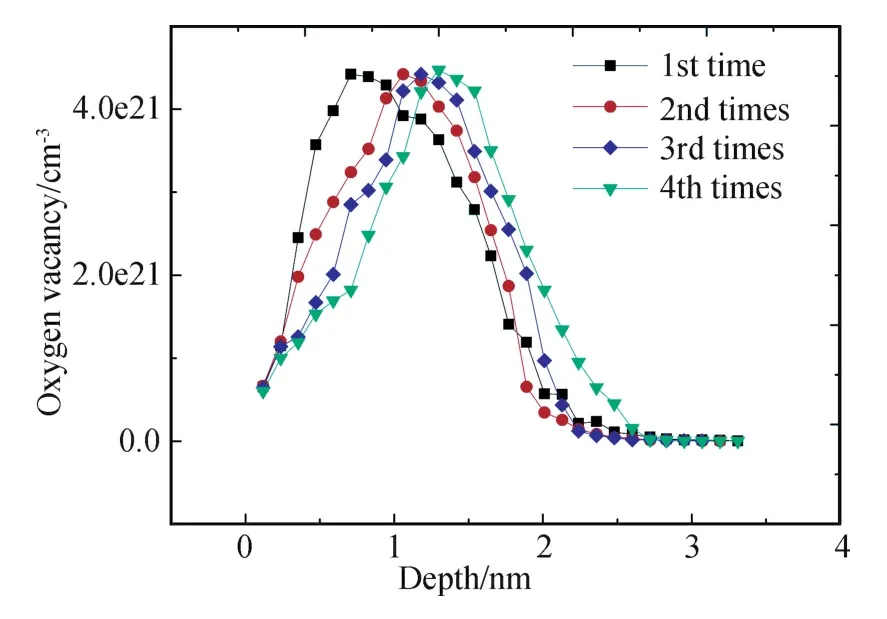
图3 前4个单位时间氧空位的分布情况Fig.3 Distribution of oxygen vacancy in the first 4 unit time
图4是表面刻蚀深度随时间的变化,拟合函数如下:
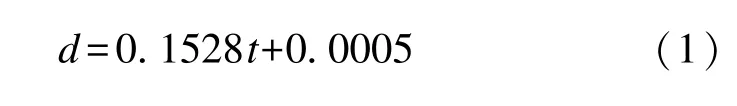
式中:d为刻蚀深度;单位是nm;t是模拟时间;单位是s。由此可知,平均刻蚀速率为0.1528 nm/s。从理论上讲,在靶材是晶体的情况下刻蚀深度与轰击时间是以零点为起点的,拟合式子中的截距0.0005属于模拟误差,但考虑到误差十分小,可以认为该直线以零点为起点。而在实验中,用原子力显微镜测得的Ar+的刻蚀深度与轰击时间的关系为d=0.15t-20[16]。由此可知,刻蚀速率与模拟结果大致符合,截距不同则是由于实际操作中材料表面本身不可能是晶体导致。

图4 表面刻蚀深度与轰击时间的关系曲线Fig.4 Relationship between surface etching depth and bombardment time
由图3中前面四次模拟计算的结果得到的非晶层厚度依次为1.1718,1.2925,1.3912,1.5113 nm,所以得到时间与非晶层厚度的关系如图5。
图5是非晶层厚度随时间的变化。在短时间内基本符合线性关系,拟合结果为
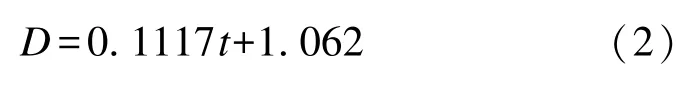
式中:t是模拟时间,单位是s;D是非晶层厚度,单位是nm。由此可知非晶层厚度的平均增长速率为 0.1117 nm/s。
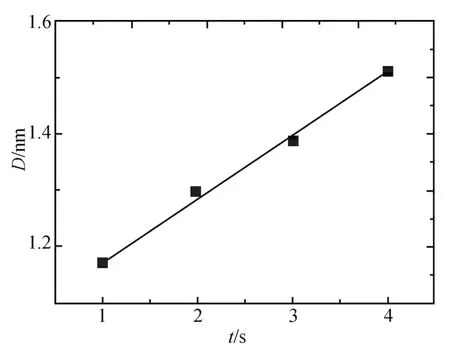
图5 非晶层厚度与时间的关系Fig.5 Relation between the thickness of amorphous layer and time
3 结论
本文提出了一种基于蒙特卡罗模拟辅助控制离子注入时间的方法,该方法以SRIM为基础,通过对时间段进行切分,然后进行迭代计算得到离子注入时间与非晶层厚度的关系。结果表明,注入时间与非晶层厚度在短时间内基本满足线性关系,非晶层厚度的平均增长速率约0.1117 nm/s。在计算时以每s为一个单位时间,但在实际的实验操作中很难精确到秒。本文只是提供一套控制离子注入时间的计算方法,在计算的过程中也可以10 s,100 s作为单位时间进行计算。文中给出了前4 s非晶层厚度与时间的关系,目的只是为了给出计算方法。实际在前500 s非晶层厚度与时间的关系都是满足线性关系的,若要得到更长时间与非晶层厚度的关系,可以照此方法进一步计算。本文是一种模拟计算的方法,从模拟结果与实验的对比差距以及模拟误差来说都是十分小的,所以该方法对实际的实验操作具有一定的辅助意义。
