浅析平面汇交力系中的力的合成问题

周元忠

【摘要】平面汇交力系是平面基本力系中的重要力系之一。研究平面汇交力系时，主要分析力的合成与平衡问题;而力的合成问题是基础也是关键。力的合成主要基于力的平行四边形公理来研究的，其核心是力的投影内容的熟练掌握。结合职校学生的教学情况分析，本文以示例加以阐述，力求深入浅出、通俗易懂;同时以期为相关学者提供借鉴与参考。

【关键词】平面汇交力系  力的合成  力的投影  力的平行四边形公理

【中图分类号】G52  【文献标识码】A 【文章编号】2095-3089（2019）51-0166-01

本文基于平面汇交力系中的共线力系、垂直正交力系与一般汇交力系这三种情形展开讨论力的合成问题。以最简单的两个力作用线汇交于一点的平面汇交力系（这里需要做出说明的是：力系是指两个以上的多个力。本文以平面汇交力系中两个力的情况为基础展开，故暂借称为力系。）入手分析探讨，进而延伸至三个力及以上的多个力作用线汇交于一点的平面汇交力系的普遍情形中。运用静力学公理中的平行四边形公理来分析力的投影相关内容。对平面汇交力系中力的合成问题，以示例分层展开述之，图文结合以求达到快速且有效地掌握与运用。

一、共线力系中的力的合成问题

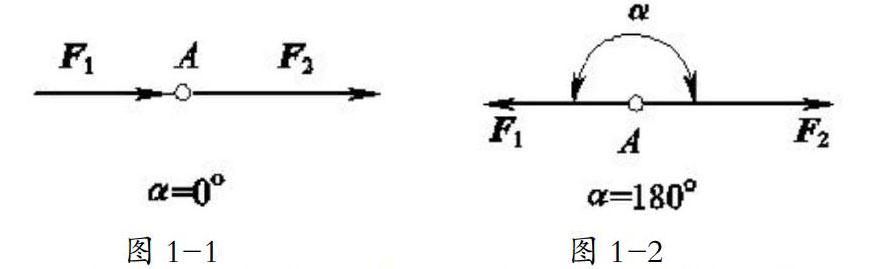
共线力系是指各力的作用方向在同一条直线上的力系。如图1-1、1-2所示， F1和F2为作用在同一条直线上的共线力。

在此前提下，求解共线力系中的力的合成问题，即求出图1-1、1-2中作用于A点的合力问题，通常做法是：取x轴的正方向为正，则它的合力大小为各力沿作用线方向的代数和。合力的指向取决于代数和的正负：正值代表作用方向与x轴同向;负值代表作用方向与x轴相反。

二、垂直正交力系中的力的合成问题

垂直正交力系作为平面汇交力系中的又一特殊力系，在讨论其力的合成问题时，仍以两个力的情况为基础展开。如图2所示。

此情形下求解力系中的力的合成问题就要运用力的平行四边形公理加以解决。力的平行四边形公理内容是作用于物体上同一点的两个力，可以合成为一个合力，合力也作用于该点上，其大小和方向可用以这两个力为邻边所构成的平行四边形的对角线来表示。所以会发现，图示中的两个力是垂直正交的两个力，构建的平行四边形恰恰是个矩形，那么其合力的求解就变成了求解该矩形的对角线这么简单了。力的平行四边形公理应用如图3所示。当然力作为矢量需要注意方向，这里是建立了坐标系，故有x轴和y轴两根轴，则仍然以x轴的正方向为正，以y轴的正方向为正。在列式中以正负号予以区分。

三、一般汇交力系中的力的合成问题

一般汇交力系中的力的合成问题，可以分为三个步骤进行。第一，将一般汇交力系中的每个力进行力在直角坐标轴上的投影，得到每个力在x轴上的投影Fix和在y轴上的投影Fiy。第二，求出合力投影。合力在任意坐标轴上的投影，等于各分力在同一轴上投影的代数和。即：FRx=F1x+F2x+…+Fnx=Fix;FRy=F1y+F2y+…+Fny=Fiy。第三，求出合力的大小和方向。若已知力在兩个坐标轴上的投影，通过力的平行四边形公理，即前面阐述的方法，可以求得。合力计算式为：FR=;其合力在两坐标轴的方向需要通过平行投影，以x轴和y轴正方向以示判断。这里，需要说明的是：本文运用的是力的平行四边形公理求得合力，严格来说，都是以平行四边形的特例——矩形（力在两坐标轴上的投影形成）来分析，这样求得的对角线很简单，即为合力大小。当然，如果运用力的三角形法则来求解力的合成问题，过程也一样。在求合力时，不一定要做出整个平行四边形。主要是因为对角线（即合力）把平行四边形分成两个全等的三角形，所以只要做出其中一个三角形即可。运用力的三角形法则时，注意将力的矢量F1和F2首尾相接（两个力的前后次序任意），再用线段将其封闭构成一个三角形，即为力的三角形，其封闭边代表合力FR。两者运用原理一样，具体计算的方便程度仁者见仁。

综上，本文是以静力学中平面汇交力系中的力的合成问题展开讨论。将平面汇交力系中的力的合成分为共线力系中的力的合成、垂直正交力系中的力的合成以及一般汇交力系中的力的合成这三种情形加以阐述，由浅入深、由易变难，循序推进。结合中职学生实际教学过程中发现，直接讲述力的投影然后求合力的课堂效果没有这样捋顺脉络、分层次地展开清晰明了。这部分内容也是后续求解力系平衡的基础乃至关键。教学中的一些心得在此分享，寄希望能对初学者有所帮助。

参考文献：

[1]人力资源和社会保障部教材办公室组织编写.全国中等职业技术学校机械类通用教材《工程力学》（第五版）.中国劳动社会保障出版社， 2011.

[2]范钦珊主编.面向二十一世纪课程教材《理论力学》（第1版）.高等教育出版社，2014.01.09.