基于各方努力水平的生鲜农产品供应链网络模型研究
2019-01-03梁薇薇周礼南周根贵陈佳佳
梁薇薇 周礼南 周根贵 陈佳佳


摘要:在生产销售过程中,生鲜农产品的质量和数量极易受到供应链成员努力水平的影响。运用网络均衡方法,构建了考虑多生产商、多零售商努力水平的生鲜农产品供应链网络模型,刻画了供应链网络成员间的竞争与合作关系,并分析了不同情形下各方努力水平对供应链网络产销及利润的影响。结果表明,在所有网络成员保持相同努力水平情形下,适当提高各方的努力水平能够提升供应链整体利润及各方利润;在各生产商之间、各零售商之间保持各自相同努力水平的情形下,生产商积极投入生产努力更有助于各方利润最大化;在生产商各自努力的情形下,生产商须密切关注竞争对手的生产努力水平,在零售商各自努力的情形下,零售商须同时关注生产商的生产努力水平与竞争对手的销售努力水平。
关键词:生鲜农产品;生产商;零售商;消费市场;供应链;努力水平;网络均衡;迭代;农产品损耗;利润;求解策略
中图分类号: F252文献标志码: A
文章编号:1002-1302(2019)21-0337-07
收稿日期:2018-08-15
基金项目:国家自然科学基金(编号:71371169)。
作者简介:梁薇薇(1992—),女,浙江绍兴人,硕士研究生,主要从事物流与供应链管理研究。E-mail:2111604036@zjut.edu.cn。
通信作者:周根贵,博士生导师,教授,主要从事物流与供应链管理研究。E-mail:ggzhou@zjut.edu.cn。
我国是荔枝的主要出产国之一,年产量为237.80余万t,约占世界的65%~70%,稳居世界第一,但年均损耗率却高达20%,经济损失超过1 000亿元[1-2]。以荔枝为例,反映出了我国生鲜农产品普遍存在“快发展”与“高损耗”相矛盾的问题,其损耗不仅包括由于产地温度、湿度不适造成的生产损耗,也包括在流通运输、储存保管过程中管理、操作不当引起的销售损耗。陈军等认为,提升努力水平可缓解生鲜农产品在流通过程中造成的数量损耗[3];杨磊等提出,生鲜农产品的市场需求依赖于零售商的努力水平,由此可见努力水平同时影响着生鲜农产品质量与数量的损耗[4-5]。基于生鲜农产品损耗严重的现实情况,促使供应链成员减少各环节损耗以改善生产、储藏、配送、销售能力成为生鲜农产品市场亟待解决的问题。
于生产商而言,《国家农业综合开发高标准农田建设规划》中指出,可通过提升在种植、培育和采摘等过程中的生产努力水平(如土壤维护、农业设备机械化投入)来提高农产品的初始质量;于零售商而言,《国家物流标准化》中提出,可通过提高运输、仓储、包装、销售等过程中的销售努力水平(如冷链物流设施投入)来降低损耗。加大供应链各方的努力水平、提升客户满意度,对推进生鲜农产品供应链管理、提升供应链整体利润及各成员利润具有重要意义。
随着社会各界对于农产品质量安全的持续关注,生鲜农产品供应链各方努力水平对农产品质量和数量的影响逐渐成为研究热点。Cachon等认为,努力水平是影响农产品需求的重要因素[6];Cai等研究了努力水平影响农产品需求情况下的供应链协调问题[7];杨磊等研究了不同契约对提升供应链各方努力水平,从而增加农产品市场需求的作用[4,8];林略等考虑了农产品的数量损耗,并在此基础上分析了农产品新鲜度对市场需求的影响[9];Lee等将农产品保鲜技术成本作为零售商的决策变量,研究其對最优订货量的影响[10];但斌等假设生产商的努力水平会影响农产品的质量与数量,提出了应对天气影响的供应链协调策略[11];王磊等研究了通过提高努力水平来降低流通损耗、提升农产品价值的方法[12];吴庆等基于第三方物流研究了努力水平对产品质量和数量的影响[13]。
然而,上述研究均未将生产商之间的产量竞争与零售商之间的销售竞争纳入考虑。随着河马鲜生、京东生鲜等各大电商巨头不断开拓生鲜市场,生产商之间的产量竞争及零售商之间的销售竞争不容忽视。因此,研究在竞争环境下生鲜农产品供应链各方努力水平对农产品质量和数量的影响具有重要的现实意义。针对此类问题,刻画供应链网络成员间竞争与合作关系并分析其均衡条件是相关研究采用的主要方法。2002年,Nagurney等首先提出了具有确定性需求的单商品流供应链网络均衡问题[14];Dong等在此基础上研究了随机市场需求的供应链网络均衡问题[15];Meng等探讨了制造商产能受到约束时的供应链网络均衡[16]。在生鲜农产品方面,Yu等建立了考虑易腐性的寡头竞争生鲜农产品供应链网络模型,并将其应用到哈密瓜市场的案例研究中[17];许强等考察了供货量损耗比对鲜活农产品供应链网络均衡的影响[18];Besik等建立了农民直销的生鲜农产品供应链网络均衡模型,并通过当地苹果生产销售的案例研究分析了供应限制及产品质量等对农民收入的影响[19]。
因此,本研究基于以上文献,构建了基于努力水平的农产品供应链网络模型,通过网络均衡方法刻画了供应链网络成员在生产、销售环节中的竞争与合作关系,并探讨了不同的竞争与合作环境中农产品多生产商与多零售商的最优努力水平及其对生鲜农产品质量、销量以及价格的影响。
1供应链网络模型描述
考虑由m个生鲜农产品生产商(以下简称生产商)和n个生鲜农产品零售商(以下简称零售商)组成的两级生鲜农产品供应链,结果如图1所示。生产商生产的是一种当季产销无库存类生鲜农产品(如水果、蔬菜、肉、蛋、水产),其具有较长的生产期和较短的销售期,因此各生产商之间、各零售商之间均存在非合作竞争。零售商通过批发市场向生产商购买农产品,并通过零售市场将农产品销售给消费者,该农产品供应链网络中各成员目标均为企业利润最大化。借鉴Lee等的研究[10,13],本研究假设农产品的初始质量受生产商生产努力水平影响,农产品的保鲜能力受零售商销售努力水平影响,供应链各方付出的努力水平越高,农产品质量越好,数量损耗越少。因此,农产品的市场需求不仅受农产品自身价格影响,还受供应链各方的努力水平共同影响。模型变量及假设如表1所示。
为便于描述,将所有生产商的产量记为m维列向量QPRm+;所有零售商的进货量记为n维列向量QRRn+;将所有生产商与零售商之间的交易量记为mn维列向量QRmn+;将所有零售商的销售价格记为n维列向量PRn+;所有生产商的实际产出率记为m维列向量LPRm+;所有零售商的实际销售率记为n维列向量LRRn+。
此外,由于生鲜农产品存放时间和销售期较短,因此生产商之间的竞争与所有生产商的总产量息息相关,丰产往往会加剧生产商之间的竞争,反之亦然。故本研究假设生产商i的竞争成本fPi(LP×QP)为生产商生产总量QP的二次连续可微凸函数,零售商j的竞争成本fRj(LR×QR)为零售商进货总量QR的二次连续可微凸函数;同理,由于生鲜农产品的运输需要较高的成本,亦假设生产商i的生产及运输总成本函数cPi(QePii)为QePii的二次连续可微凸函数、零售商j的总运输成本函数cRj(QeRjj)为QeRjj的二次连续可微凸函数,生产商i与零售商j之间的交易成本函数tPij(qij)、tRij(qij)均为qij的二次连续可微凸函数。参考文献[11],假设努力成本g(e)=12ke2为努力水平e的二次连续可微凸函数。
2供應链网络模型构建
本研究考虑m个生产商和n个零售商组成的两级生鲜农产品供应链,构建了如下网络模型。假设农产品的质量和数量受供应链网络中生产商生产努力水平和零售商销售努力水平共同影响,随着努力水平的提升,农产品质量越好,损耗越少。生产商与零售商根据利润最大化原则,决策努力水平、交易量以及交易价格。
生产商i的最优模型:
maxπPi=∑nj=1pijqij=cPi(QePii)-fPi(LP×QP)-g(ePi)-∑nj=1tPij(qij);
s.t.0≤ePi≤1,i;
0≤QePii≤Qi,i;
∑nj=1qij≤lPi·QePii,i,j;
qij≥0,i,j。(1)
式中:∑pijqij为生产商的销售收入;cPi(Qeipi)为生产及运输成本;fPi(LP×QP)为竞争成本;g(epi)为努力成本;第5项为交易成本。
零售商j的最优模型:
maxπRj=∑mi=1lRjpijqij-cRj(QeRjj)-fRj(LR×QR)-g(eRj)-
∑mi=1tRij(qij)-∑mi=1pijqij;
s.t.0≤eRj≤1,j;
0≤QeRjj≤∑mi=1qij,i,j。(2)
式中:第1项为零售商的销售收入;第2项为运输成本;第3项为竞争成本;第4项为努力成本;第5项为交易成本;第6项为采购成本。
3供应链网络模型求解策略
本研究的网络模型包含多个生产商和多个零售商,属于非线性优化问题,常规的逆向推导难以求解,故针对该模型特点,本研究运用网络均衡方法进行求解,将其转化为网络均衡模型。求解步骤如下:(1)随机给定初始生产商与零售商努力水平;(2)将随机给定的努力水平代入目标函数,将其转化为网络均衡模型,采用对数二次型预测与校正算法,即LQP-PC算法对该网络模型进行求解,得到既定努力水平下的农产品产销量、售价以及各方利润;(3)根据利润最大化原则,不断迭代得到生产商与零售商的最优产销决策,其对应的努力水平即为最优努力水平。
3.1努力水平的确定
基于本研究对生产商、零售商努力水平的描述,为方便量化和刻画上述供应链各方的努力水平,本研究将生产商、零售商努力水平假设为高、中、低3个标准。土壤层厚大于20 cm且引入3项及以上先进适用技术的生产商定义为高标准生产商,土壤层厚10~20 cm且引入至少1项先进适用技术为中标准生产商,土壤层厚低于10 cm且无先进适用技术引入为低标准生产商,其对应的生产努力水平范围分别为(0.7,1]、(0.3,0.7]、(0,0.3];将运输、仓储、包装、销售4个过程中均采用冷链物流硬件设备的零售商定义为高标准零售商,其中2个或3个过程采用冷链物流硬件设备的为中标准零售商,仅1个过程采用或未采用冷链物流硬件设备的为低标准零售商,零售商分别对应的努力水平为(0.7.1]、(0.3,0.7]、(0,0.3]。
3.2网络均衡模型的构建
随机给定各生产商与各零售商努力水平,对既定努力水平下的模型进行研究,构建如下网络均衡模型。
3.2.1生产商均衡条件
生产商在生产期前决策产量,在销售期决策在批发市场交易的数量并将其销售给零售商。同时,生产商与零售商交易过程中会产生交易成本,且受到来自其他生产商的竞争,最后也须要考虑生产努力成本。故生产商i的利润函数为:
maxπPi=∑nj=1pijqij-cPi(QePii)-fPi(LP×QP)-g(ePi)-∑nj=1tPij(qij);
s.t.QePii≤Qi,i;
∑nj=1qij≤lPi·QePii,i,j。(3)
式中:第1个约束条件公式对应生产商i的产量上限约束,第2个对应生产商i生产销售产品的产销约束,设其对应Lagrange乘子分别为μi、ηi,所有的μi、ηi分别构成m维列向量μ、η。各生产商间为非合作竞争关系,因此所有生产商的最优行为可等价表示为如下变分不等式问题:确定(QP*,Q*,μ*,η*)ΩP,使其满足:
∑mi=1cP*i(QePii)QePii+fP*i(LP×QP)QePii+μ*i-η*ilPi(QePii-QeP*ii)+
∑mi=1∑nj=1tP*ij(qij)qij+η*i-p*ij(qij-q*ij)+∑mi=1(Qi-QePii)
(μi-μ*i)+∑mi=1lPi×QePii-∑nj=1qij(ηi-η*i)≥0;(4)
(QP*,Q*,μ*,η*)ΩP,其中,ΩP=Rm+mn+m+m+。
均衡状态下,由式(4)第1项可知,η*ilPi=cP*i(QePii)QePii+fP*i(LP×QP)qePii+μ*i;又由式(4)第2项可知η*i=p*ij-tP*ij(qij)qij,合并得到μ*i-lPip*ij-tP*ij(qij)qij-cP*i(QePii)QePii-fP*i(LP×QP)QePii。故式(4)的经济学意义为生产商只有在交易价格大于交易成本、生产及运输成本、竞争成本之和时才会从事生鲜农产品生产。
3.2.2零售商均衡条件
零售商在销售期前决策向生产商订购的农产品数量,在销售期决策农产品的销售价格以满足市场需求,同时零售商在交易过程中会产生交易成本,并受其他零售商的竞争,最后也须要考虑销售努力成本。故零售商j的利润函数为:
maxπRj=∑mi=1lRjpijqij-cRj(QeRjj)-fRj(LR×QR)-g(eRj)-
∑mi=1rRij(qij)-∑mi=1pijqij;
s.t.QeRjj≤∑mi=1qij,i,j。(5)
式中:不等式对应零售商j销售产品的供銷约束,设约束不等式对应Lagrange乘子分别为γj,所有的γj分别构成n维列向量γ。所有零售商的最优行为可等价表示为如下变分不等式问题:确定(QR*,Q*,γ*)ΩR,使其满足:
∑nj=1cR*j(QeRjj)QeRjj+fR*j(LR×QR)QeRjj+γ*j(QeRjj-QeR*jj)+∑nj=1∑mi=1
rR*ij(qij)qij+p*ij-pi*jlRj-γij(qij-q*ij)+∑nj=1∑mi=1
(qij-QeRjj)(γj-γ*j)≥0;
(QR*,Q*,γ*)ΩR。(6)
式中:ΩR=Ωn+mn+n+。
均衡状态下,合并式(6)前2项,可得pi*j=p*ij+cR*j(QeRjj)QeRjj+fR*j(LR×QR)QeRjj+tR*ij(qij)qij/lRj,故式(6)的经济学意义为农产品零售价格随生产商与零售商间的交易价格以及零售商的各类边际成本的增加而增加。此外,农产品零售价格也受零售商努力水平的影响,零售商提高努力水平有助于减少农产品的损耗,从而降低农产品的市场价格。
3.2.3消费市场均衡条件
在销售期,零售商向消费市场销售农产品,消费者根据价格、质量和数量选购农产品。对于零售商j而言,需求市场对农产品的需求均衡条件可以表示为[20]:
Dij=lRjqij,pij>0
≤lRjqij,pij=0。(7)
整个需求市场的均衡条件可等价表示为如下变分不等式问题:确定P∈ΩM,使其满足:
∑nj=1(lRjqij-Dij)(pij-pi*j)≥0;
P∈ΩM。(8)
式中:M代表市场;ΩM=Rn+。
3.2.4供应链网络均衡
当所有生产商、零售商以及市场交易量和交易价格满足最优条件时,整个供应链网络达到均衡。因此,结合式(4)、式(6)和式(8),可整理得到整个供应链网络的均衡条件,即(QP*,Q*,QR*,P*,μ*,η*,γ*)∈Ω确定,满足:
∑mi=1cP*i(QePii)QePii+fP*i(LP×QP)QePii+μ*i-η*ilPi(QePi-QeP*ii)+
∑mi=1∑nj=1tP*ij(qij)qij+tR*ij(qij)qij-pi*jlRj+η*i-γ*j(qij-q*ij)+
∑nj=1cR*j(QeRjj)QeRjj+fR*j(LR×QR)QeRjj+γ*j(QeRjj-QeR*jj)+
∑nj=1(lRjqij-Dij)(pij-pi*j)+∑mi=1(Qi-QePii)(μi-μ*i)+
∑mi=1lPi×QePii-∑nj=1qij(ηi×η*i)+
∑nj=1∑mi=1qij-QeRjj(γj-γ*j)≥0;
(QP*,Q*,QR*,P*,μ*,η*,γ*)Ω。(9)
式中:Ω=ΩP×ΩR×ΩM。
在模型中,生产商i与零售商j间的农产品交易价格pij为内生变量,当供应链网络间交易达到均衡时,由式(9)可知,若qij>0,则
p*ij=η*i+TP*ij(qij)qij。(10)
求解变分不等式的算法主要有修正投影收缩算法[21]和对数二次型预测与校正算法[22]等。其中,基于对数二次型近似算法[23]的LQP-PC算法,不仅能够求解多面体可行域上变分不等式的全局最优解,而且计算总成本非常小[22],因此其广泛应用于求解带有产量、价格等约束的供应链网络均衡问题[24]。本研究提出的模型带有产量上限约束,故变分不等式(9)的可行域为多面体,因而采用LQP-PC算法对该网络均衡模型进行求解。
3.3迭代
重复上述步骤,依次选取供应链各方努力水平代入网络均衡模型,从网络均衡模型得到的结果中根据利润最大化原则,选择利润最大的作为生产商和零售商各自的最优产销决策,其对应的努力水平即为最优努力水平。
4基于努力水平的供应链网络模型分析
假设农产品供应链网络由2个生产商、2个零售商以及需求市场构成,即i=1,2;j=1,2。主要参数设置如下:生产商i的农产品产量上限Qi=+∞;生产商i的竞争成本fPi=0.25(lPiQePii)2+0.5(lPiQePii)(lP3-iQePi3-i)+lPiQePii;零售商j的竞争成本fRi=0.5(lRjQeRjj)2;生产商i与零售商j交易时的交易成本tPij=0.25q1ij+0.5qij,零售商j与生产商i交易时的交易成本tRij=0.5q2ij+3qij;生产商i生产及运输总成本cPi=QePii,零售商j运输总成本cRj=QeRjj;参考文献[6],假设生产商i的实际到达率lPi=1-(0.25+ePi)-1·λ,零售商j的实际到达率lRj=1-(0.25+eRj)-1·λ,市场对零售商j的农产品期望需求量Dij=(a-bpij)θPiθRj,其中θPi=ePi,θRj=eRj,a=600,b=1.8,λ=0.125。以上需求函数设置确保:(1)零售商农产品销售价格越高,其面临需求越小;(2)生产商生产努力水平及零售商销售努力水平越高,农产品需求越大。
为研究不同竞争与合作环境中供应链各方的最优努力水平及其影响,以下对比分析3种不同情形下供应链网络模型的均衡结果,从而为相关企业提供决策依据。
4.1情形一:所有网络成员保持相同努力水平
在该情形下,所有网络成员保持相同努力水平,即eP1=eP2=eR1=eR2,有产量上限和无产量上限时,产销努力水平对供应链网络整体及各方利润的影响分别如图2、图3所示,其中i=1、2,j=1、2。πPi表示生产商i的利润,πRj表示零售商j的利润,π表示二者之和,下同。
从图2可以看出,随着生产商及零售商努力水平的协同增加,供应链总利润先增后减,并在努力水平为0.9时取得最大值;所有网络成员处于较低或较高的努力水平时,整体及各成员的利润增幅较缓,而努力水平处于中间一定范围内时,随着努力水平增加,利润上升幅度显著增加。可见,生产商和零售商努力水平处于起步阶段时,提高努力水平对利润的增加并不显著,但随着努力水平的不断提升,双方的利润增幅都会呈现显著增加的趋势,因此供应链各方应当持续投入努力,从而实现合作共赢。
从图3可以看出,当外界因素导致农产品产量受限,需求市场上供不应求时,供应链总体利润小幅度上升。随着双方努力水平的增加,生产商利润持续增加,且相较于产量不受限时增加显著,而零售商的利润仍保持先增后减,但相较于产量不受限时有所下降。因此,當外界因素导致农产品减产时,生产商与零售商的利润不再随着努力水平改变而同步改变,双方将难以保持一致的努力水平。
4.2情形二:各生产商保持相同努力水平,各零售商保持相同努力水平
在该情形下,各生产商保持相同努力水平,各零售商保持相同努力水平,即eP1=eP2,eR1=eR2。在对方采取不同的生产努力水平或销售努力水平情况下,零售商或生产商应对的最优努力水平及供应链均衡结果如表2所示。
随着生产商努力水平ePi从0~1的改变,零售商的最优努力水平eRj从0.7上升至0.9,呈现小幅度上升趋势,与“情形一”下的零售商最优努力水平基本保持一致;而零售商努力水平eRj从0~1的改变过程中,生产商最优努力水平始终保持在0.7,低于“情形一”下的生产商最优努力水平。因此,在该情形下,生产商积极投入努力更有助于提升供应链的努力水平及整体利润。
4.3情形三:生产商各自努力或零售商各自努力
4.3.1生产商各自决策自身的努力水平
在该情形下,生产商各自决策自身努力水平,零售商保持一致努力水平,即eP1≠eP2,eR1=eR2。在不同的零售商和竞争对手努力水平下,生产商应对的最优努力水平及供应链均衡结果如表3所示。
当生产商1努力水平eP1从0~1变化时,不论零售商处于低努力水平或是处于高努力水平,生产商2的最优努力水平eP2均高于“情形二”的生产商最优努力水平。但随着生产商1努力水平eP1的提高,生产商2的最优努力水平eP2有所下降。因此,在该情形下,生产商无须顾及零售商采取何种努力水平,但须要观察竞争对手的努力水平,从而作出最优决策,保持相对较高的努力水平。
4.3.2零售商各自决策自身的努力水平
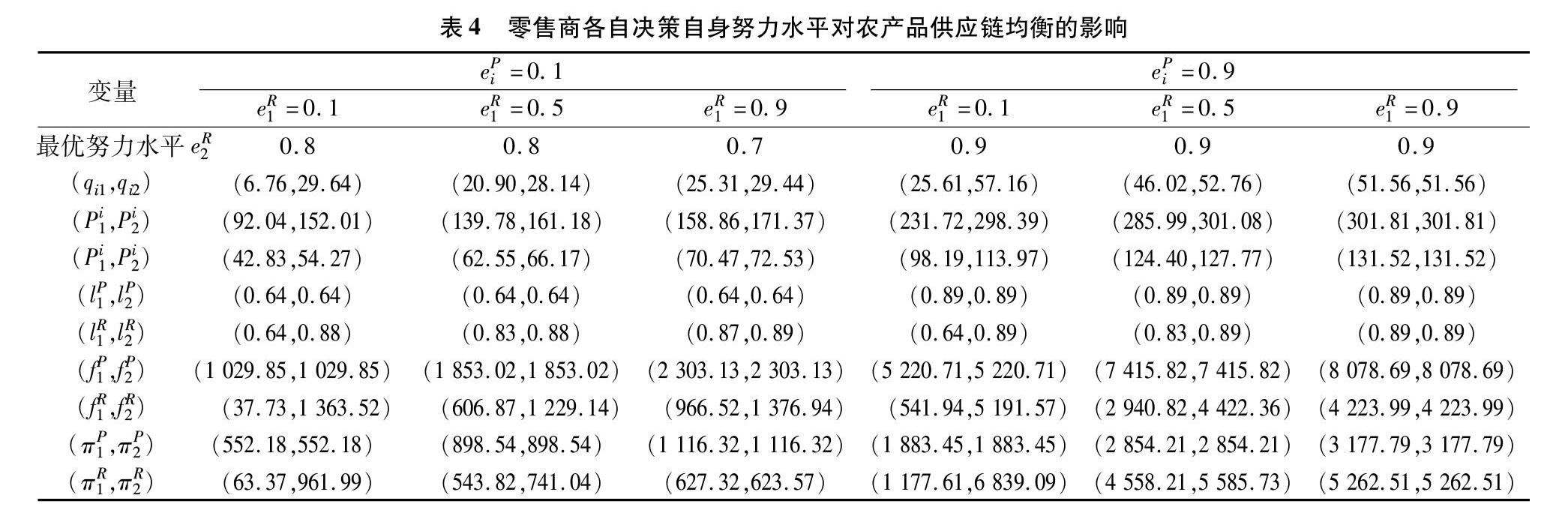
在该情形下,零售商各自决策自身努力水平,生产商保持一致努力水平,即eP1=eP2,eR1≠eR2。在不同的生产商和竞争对手努力水平下,零售商应对的最优努力水平及供应链均衡结果如表4所示。
当生产商处于低努力水平时,随着零售商1努力水平eR1从0~1递增变化时,零售商2的最优努力水平eR2有所下降,且低于“情形二”下的零售商最优努力水平;当生产商处于高努力水平时,零售商2的最优努力水平eR2不随零售商1努力水平eR1改变而改变,始终保持在0.9,与“情形二”下的零售商最优努力水平保持一致。因此,在该情形下,生产商若处于高努力水平,零售商须付出高努力水平来保证自身利润的最大化;反之,零售商则须要观察竞争对手的努力水平而作出最优决策。当竞争对手处于较高努力水平时,适当降低自身努力水平,有利于提高自身利益。
5结束语
农产品供应链各方的努力水平是影响农产品质量和数量的关键因素。同时,随着各大电商巨头不断开拓生鲜市场,农产品供应链网络中的竞争亦不容忽视。针对上述农产品生产销售的实际问题,本研究构建了基于努力水平的供应链网络模型,通过基于迭代和对数二次型预测与校正算法的混合策略对模型进行求解,探讨了竞争与合作环境中供应链网络成员的最优努力水平及其对生鲜农产品质量、销量以及价格的影响。结果表明:(1)在所有网络成员保持相同努力水平情形下,适当提高供应链各方的产销努力水平能够有效促进市场需求,提高产销,且供应链整体利润、各成员利润及最优努力水平均高于其他情形。因此,生鲜电商等零售企业可以通过签订契约或达成战略合作等模式,与农产品生产商相互合作,形成经济共同体,实现供应链整体及各方利润最大化;大型超市等零售商可通过“农超对接”等措施,与农产品生产商形成全面合作局面,实现双赢。(2)当外界因素导致市场上农产品供不应求时,随着所有网络成员协同增加产销努力水平,供应链整体利润及零售商利润均呈现先增后减的变化趋势,而生产商的利润则持续增加,双方的努力水平难以保持一致。因此,生产商为保证自身利润最大化,在不断提升自身生产努力水平的同时,还应采取一定激励措施促进零售商提高销售努力水平。(3)当各生产商保持相同努力水平、各零售商保持相同努力水平时,生产商积极投入生产努力更有助于提升供应链的努力水平及整体利润。且与所有成员保持相同努力水平情形相比,生产商最优生产努力水平有所下降,零售商最优销售努力水平则基本保持不变。因此,对于农业生产合作社而言,应适当采取财政补贴、设施设备引进等政策激励农户提高生产努力水平,保证农产品初始质量的高标准。(4)在生产商各自决策自身努力水平的情形下,生产商较高的生产成本是其利润损失的主要原因,且其自身努力水平的决策受到竞争对手努力水平的影响。随着竞争对手努力水平的提高,自身最优努力水平呈现小幅度下降趋势,但高于生产商、零售商保持相同努力水平情形下的生产商最优生产努力水平,同时受零售商等下游企业的努力水平影响较小。因此,对于零散农户而言,其须要密切关注竞争对手以决策自身最优努力水平。(5)在零售商各自决策自身努力水平的情形下,若生产商处于高生产努力水平,会促使零售商选择高努力水平,且零售商的最优努力水平不受竞争对手努力水平影响;若生产商处于低生产努力水平,零售商的最优努力水平与竞争对手努力水平相关,当竞争对手处于较高努力水平时,零售商适当降低自身努力,有利于提高自身利润。因此,农产品连锁超市等零售商散户应积极建立生鲜农产品配送中心,提高农产品配送率,支持农产品冷链设施建设,延长农产品销售期,且须密切关注生产商与竞争对手的努力水平来决策自身努力水平,以获得较高利润。
本研究仍存在一些不足,如未考虑供应链各方的风险偏好等,未来可将该研究拓展至不同风险偏好或不同性质的生产商及零售商情形;此外,本研究仅考虑了单一生鲜农产品,未来可对考虑多种农产品的多层次生鲜农产品供应链网络进行探讨。
参考文献:
[1]Wu Y J,Lin H T,Lin Y F,et al. Effects of biocontrol bacteria Bacillus amyloliquefaciens LY-1 culture broth on quality attributes and storability of harvested litchi fruit[J]. Postharvest Biology and Technology,2017,132:81-87.
[2]Zhang Z K,Hu M J,Yun Z,et al. Effect of tea seed oil treatment on browning of litchi fruit in relation to energy status and metabolism[J]. Postharvest Biology and Technology,2017,132:97-104.
[3]陈军,但斌. 努力水平影响流通损耗的生鲜农产品订货策略[J]. 工业工程与管理,2010,15(2):50-55.
[4]杨磊,肖小翠,张智勇. 需求依赖努力水平的生鲜农产品供应链最优定价策略[J]. 系统管理学报,2017,26(1):142-153.
[5]覃燕红,徐丹丹. 需求依赖努力的批发价格契约协调——基于公平偏好信息非对称的分析[J]. 商业研究,2017(8):1-11.
[6]Cachon G P,Lariviere M A. Supply chain coordination withrevenue-sharing contracts:strengths and limitations[J]. Management Science,2005,51(1):30-44.
[7]Cai X Q,Chen J,Xiao Y B,et al. Optimization and coordination of fresh product supply chains with freshness-keeping effort[J]. Production and Operations Management,2010,19(3):261-278.
[8]胡本勇,王性玉. 考虑努力因素的供应链收益共享演化契约[J]. 管理工程学报,2010,24(2):135-138,134.
[9]林略,杨书萍,但斌. 时间约束下鲜活农产品三级供应链协调[J]. 中国管理科学,2011,19(3):55-62.
[10]Lee Y P,Dye C Y. An inventory model for deteriorating items under stock-dependent demand and controllable deterioration rate[J]. Computers & Industrial Engineering,2012,63(2):474-482.
[11]但斌,伏紅勇,徐广业,等. 考虑天气与努力水平共同影响产量及质量的农产品供应链协调[J]. 系统工程理论与实践,2013,33(9):2229-2238.
[12]王磊,但斌. 考虑零售商保鲜和消费者效用的生鲜农产品供应链协调[J]. 运筹与管理,2015,24(5):44-51.
[13]吴庆,但斌,钱宇,等. 努力水平影响损耗的低值易逝品TPL协调合同[J]. 管理科学学报,2014,17(12):15-26.
[14]Nagurney A,Dong J,Zhang D. A supply chain network equilibrium model[J]. Transportation Research Part E-Logistics and Transportation Review,2002,38(5):281-303.
[15]Dong J,Zhang D,Nagurney A. A supply chain network equilibrium model with random demands[J]. European Journal of Operational Research,2004,156(1):194-212.
[16]Meng Q,Huang Y K,Cheu R L. Competitive facility location on decentralized supply chains[J]. European Journal of Operational Research,2009,196(2):487-499.
[17]Yu M,Nagurney A. Competitive food supply chain networks with application to fresh produce[J]. European Journal of Operational Research,2013,224(2):273-282.
[18]许强,曾美花,王应明. 基于供货量损耗比的鲜活农产品均衡问题研究[J]. 工业工程,2015,18(2):59-65.
[19]Besik D,Nagurney A. Quality in competitive fresh produce supply chains with application to farmers markets[J]. Socio-economic Planning Sciences,2017,60:62-76.
[20]Nagurney A. On the relationship between supply chain and transportation network equilibria:a supernetwork equivalence with computations[J]. Transportation Research(Part ELogistics and Transportation Review),2006,42(4):293-316.
[21]Korpelevich G M. The extragradient method for finding saddle points and other problems[J]. Matecon,1976,12:747-756.
[22]He B S,Xu Y,Yuan X M. A Logarithmic-quadratic proximal prediction-correction method for structured monotone variational inequalities[J]. Computational Optimization and Applications,2006,35(1):19-46.
[23]Auslender A,Teboulle M,Ben-Tiba S. A logarithmic-quadratic proximal method for variational inequalities[J]. Computational Optimization and Applications,1999,12(1/2/3):31-40.
[24]胡劲松,李增强,胡小根,等. 具有产能约束和价格干预的供应链网络双渠道均衡[J]. 计算机集成制造系统,2012,18(4):849-858.
