增压器压气机叶轮的弹塑性分析

2019-01-03马元浩吴昌华陈秉智

大连交通大学学报 2018年6期

马元浩, 吴昌华, 陈秉智

(大连交通大学机车车辆工程学院，辽宁大连 116028)*

0 引言

增压器作为柴油机的重要组成部分，可使柴油机的功率、经济性能得以极大提高[1]，因此增压器的性能和寿命对柴油机来说是极其重要的.随着增压器向高转速、高功率以及高增压方向发展[2]，压气机压比和转速不断增大，叶轮所受的载荷不断增加.叶轮一般采用铝合金制造，延性范围小，在压气机高速旋转时，产生的巨大离心力使叶轮根部产生塑性变形，使其强度受到极大影响，这会影响整个增压器的安全运行[3].目前叶轮设计时对其强度分析大多是按照弹性处理，不考虑塑性变形，应力分析不够精确[4].因此，有必要对压气机叶轮进行弹塑性有限元数值分析.

近代国内外学者针对叶轮的弹塑性问题进行了一系列的研究.廖爱华[5]使用了基于参变量变分原理的有限元参数二次规划法结合多重子结构的方法进行了压气机叶轮的弹塑性分析.但由于节点数和单元数相对较少，不能全面反映真实的叶轮应力和应变.高兴[6]将材料的本构关系曲线进行了适当的假设与简化，把材料近似看成“弹-线”性强化材料，以此计算得到了高转速时弹性变形区域与塑性变形区域的解析解.虽然这种方法简化了叶轮的弹塑性问题的分析，但存在着显著的局限性，会造成理论计算结果与实际结果之间产生较大的误差.Choubey[7]利用液压机进行试验，研究不同压力对叶轮表面的应力、位移及塑性应变的影响.虽然贴合工程实际，但缺乏一定的理论支持.

本文利用Hypermesh有限元分析软件建立叶轮整体的三维有限元网格模型，将节点数和单元数扩大，细化叶根应力集中部分的网格，随后将其导入大型有限元分析软件ABAQUS中进行弹性和弹塑性分析[8]，并在弹性和弹塑性状态下，针对叶轮的不同转速对应力及位移的影响进行对比分析，结果表明弹塑性分析是合理的，是更符合工程实际的.

1 计算理论

塑性力学有形变理论和流动理论两种理论.形变理论又称全量理论，是以变形的全量作为分析的基础，因此分析问题的方法与弹性力学是一致的.流动理论又称增量理论[9]，其特点是从应力与应变增量关系入手来研究材料在塑性状态时的力学行为，因而不受加载途径的限制，这是它的一个重要优点.本文就是利用增量理论分析叶轮整体的弹塑性问题.

(1)平衡方程

A(▽)dσ+db=0

(1)

dε=L(▽)du

(2)

(3)边界条件

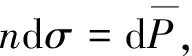
在Sp上

(3)

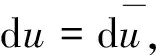
(4)

(4)本构关系

dσ=D(dε-dεp)

(5)

f(σ,εp,k)≤0

(6)

(7)

(8)

分析上述方程可以发现，式(1)～(8)与弹性力学边值问题类似，所不同的是在这里是用的增量表达式，而本构关系则有很大的不同.

ABAQUS软件对于分析材料非线性问题具有强大的模拟性能[10]，它采用直接法，直接对刚度矩阵求逆，进而得到位移解.ABAQUS软件在求解弹塑性问题时，把分析过程划分为一系列的载荷增量步，在每个增量步内进行若干次迭代，得到可接受的解后，再求解下一个增量步，所有增量响应的总和就是弹塑性分析的近似解. ABAQUS软件对弹塑性问题的计算过程与理论计算过程存在一定的差异，对比图如图1所示.

由图1可以看出，混交度的分布频率随着混交等级的增高而增大。从表1可以看出，全林分的平均混交度是0.7676，属强度混交向极强混交过渡状态，其中极强混交占48.4%，强度混交占24.4%，两者合计占72.8%，处于零度混交和弱度混交的林木相对较少，两者之和约10%，说明整体林分处于高度混交状态。

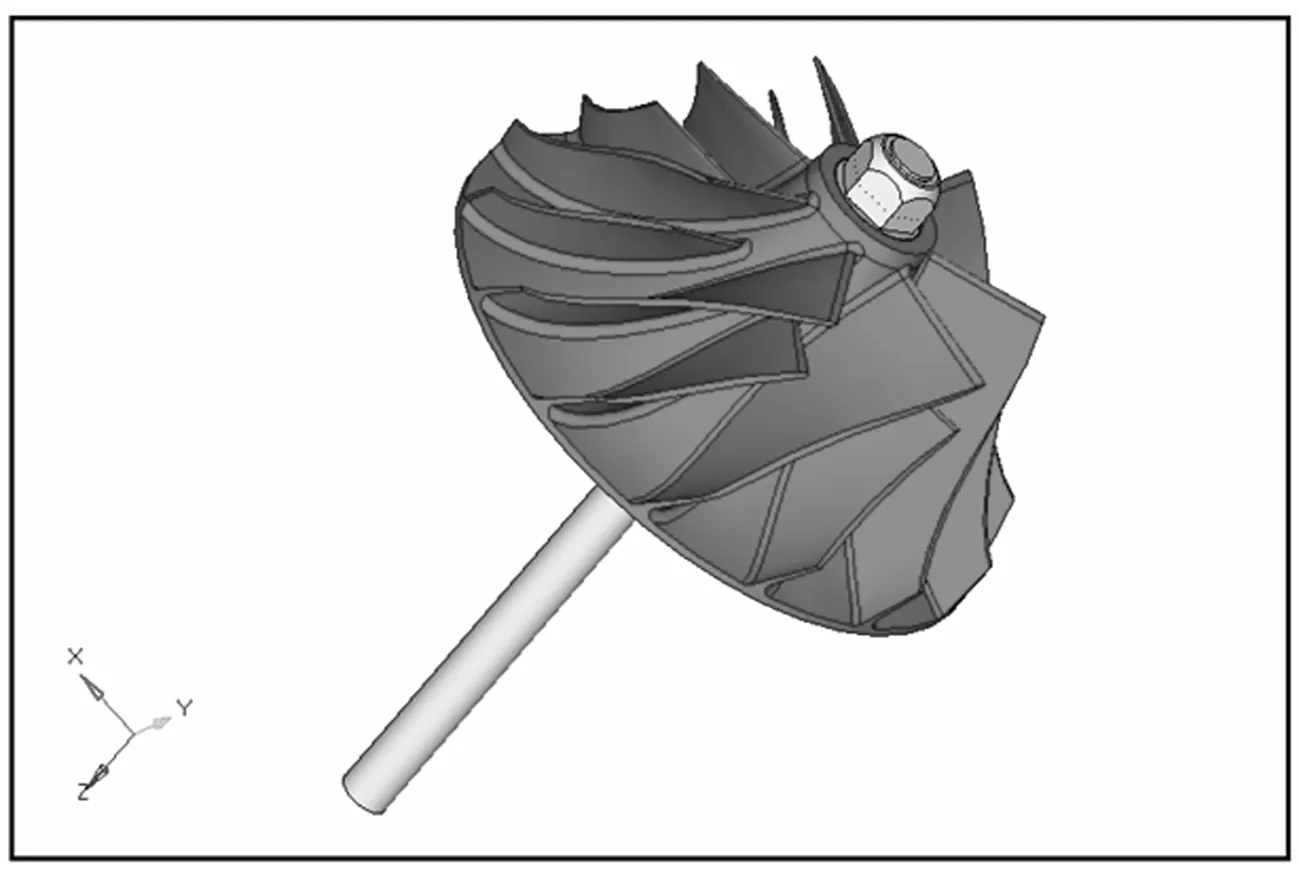
图1 ABAQUS计算过程与理论计算过程对比图

2 计算模型的建立

某增压器压气机叶轮为整体式结构，包括叶轮、螺母、螺栓和垫片，它们通过螺栓预紧装配起来.由于所研究的主要对象是叶轮，所以可以将螺栓、螺母和垫片简化处理，将螺栓简化为一个形状为圆柱体的轴，将螺栓、螺母和垫片作为一个整体，以此节约计算成本，提高计算效率.叶轮沿圆周循环对称地布置有14个叶片，叶片采用前倾后弯的结构，形成径向流道，而且叶片在出口处朝轮盘方向倾斜，同时叶片长、短相间分布，这样的结构可以使压气机工作效率更高，特性更宽[11].如图2为叶轮整体结构的几何模型.

图2 叶轮整体结构的几何模型

表1为叶轮的主要尺寸和转速.叶轮的材料为LD7锻铝，螺母、螺栓和垫片的材料为42CrMoA高强度钢，表2为LD7锻铝和42CrMoA高强度钢的材料属性.

表1 叶轮的主要尺寸

表2LD7锻铝和42CrMoA高强度钢的材料属性

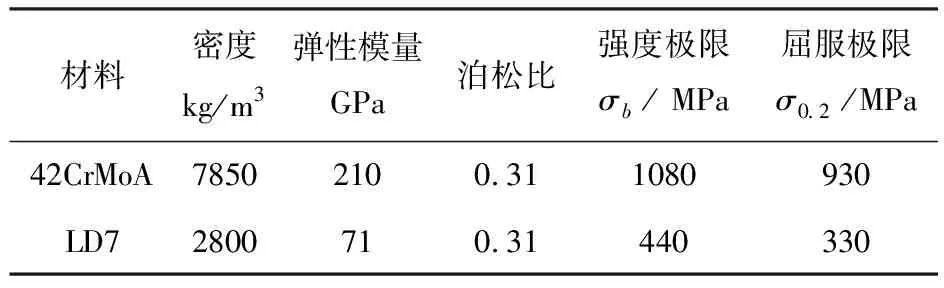
材料密度kg/m3弹性模量GPa泊松比强度极限σb/ MPa屈服极限σ0.2/MPa42CrMoA78502100.311080930LD72800710.31440330

利用Hypermesh软件依据叶轮整体结构进行有限元建模，对其全部采用C3D4单元类型(四节点线性四面体单元)进行网格划分[12]，总体单元边长尺寸约为3 mm，对容易产生应力集中的叶轮根部进行网格细化，细化处最小单元边长尺寸为1 mm.叶轮整体的网格图如图3所示.

图3 叶轮整体的网格图

叶轮整体模型中节点总数78318个，单元总数为348439个，最小单元边长为1 mm.

压气机叶轮受力主要为转速产生的巨大离心力.工作状态下的叶轮，产生的热应力不大，温度对叶轮强度的影响较小，所以在有限元分析时可以忽略.而且跟涡轮对比，在叶轮上由气动力产生的压力负荷一般比较小，所以也可以忽略.故本文只考虑离心力的影响.

3 叶轮整体的弹性有限元分析

将Hypermesh软件画出的叶轮整体网格模型导入到ABAQUS软件中，利用ABAQUS软件对叶轮的5种转速(n=40 000r/min，n=45 000r/min，n=50 000 r/min，n=55 000 r/min，n=60 000 r/min)进行弹性有限元计算.在分析过程中选用一般静态分析类型Static，General，初始增量步大小设为0.01，总分析步时间设为1.计算模型必须要消除刚体在空间的6个自由度，为此约束轴顶端所有节点的Z方向自由度(U3=0)；约束轴顶端其中一点的X方向自由度(U1=0)；约束轴顶端其中一点的X、Y方向自由度(U1=U2=0).同时对其施加载荷，即由转速引起的离心力[13].

叶轮整体在额定转速下的总位移如图4所示.

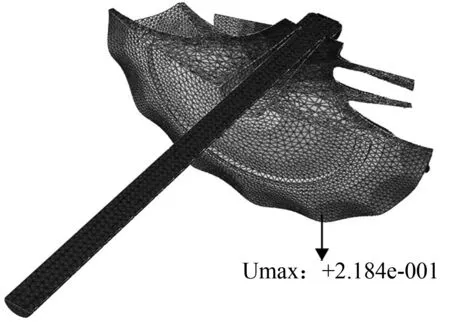
图4 叶轮整体在额定转速下的总位移图

叶轮整体的最大位移随转速变化的规律曲线如图5所示.

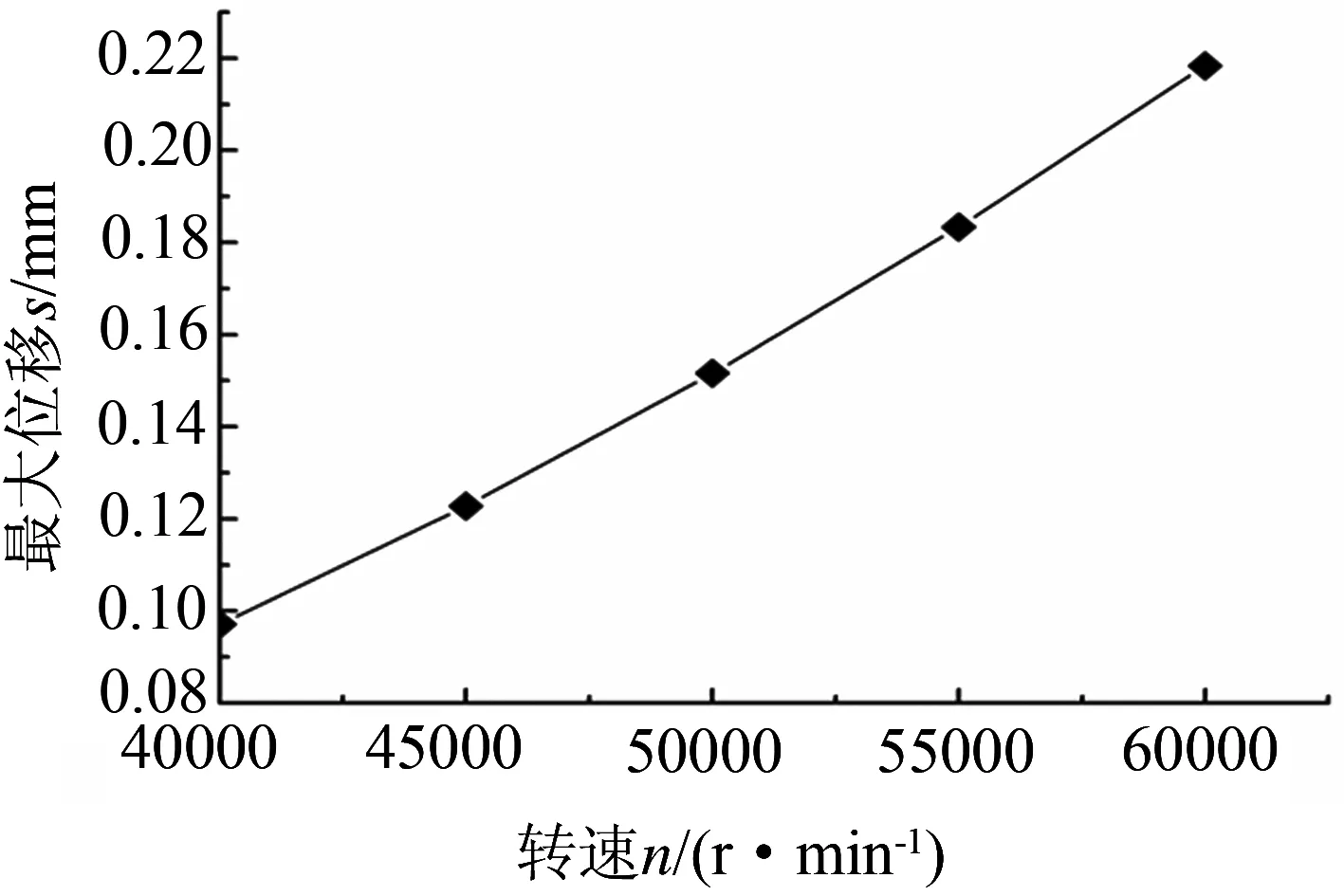
图5 叶轮整体的最大位移随转速变化的规律曲线

由图4可以看出，最大位移出现在叶轮轮盘边缘.随着叶轮结构的半径越来越小，位移越来越小，这是由于叶轮轮盘边缘质量小，叶轮、螺母、垫片等与轴连接处质量较大的缘故.由图5可以看出，随着转速的增大，叶轮整体的最大位移也随之增大.

叶轮整体在额定转速下的Mises应力如图6所示.

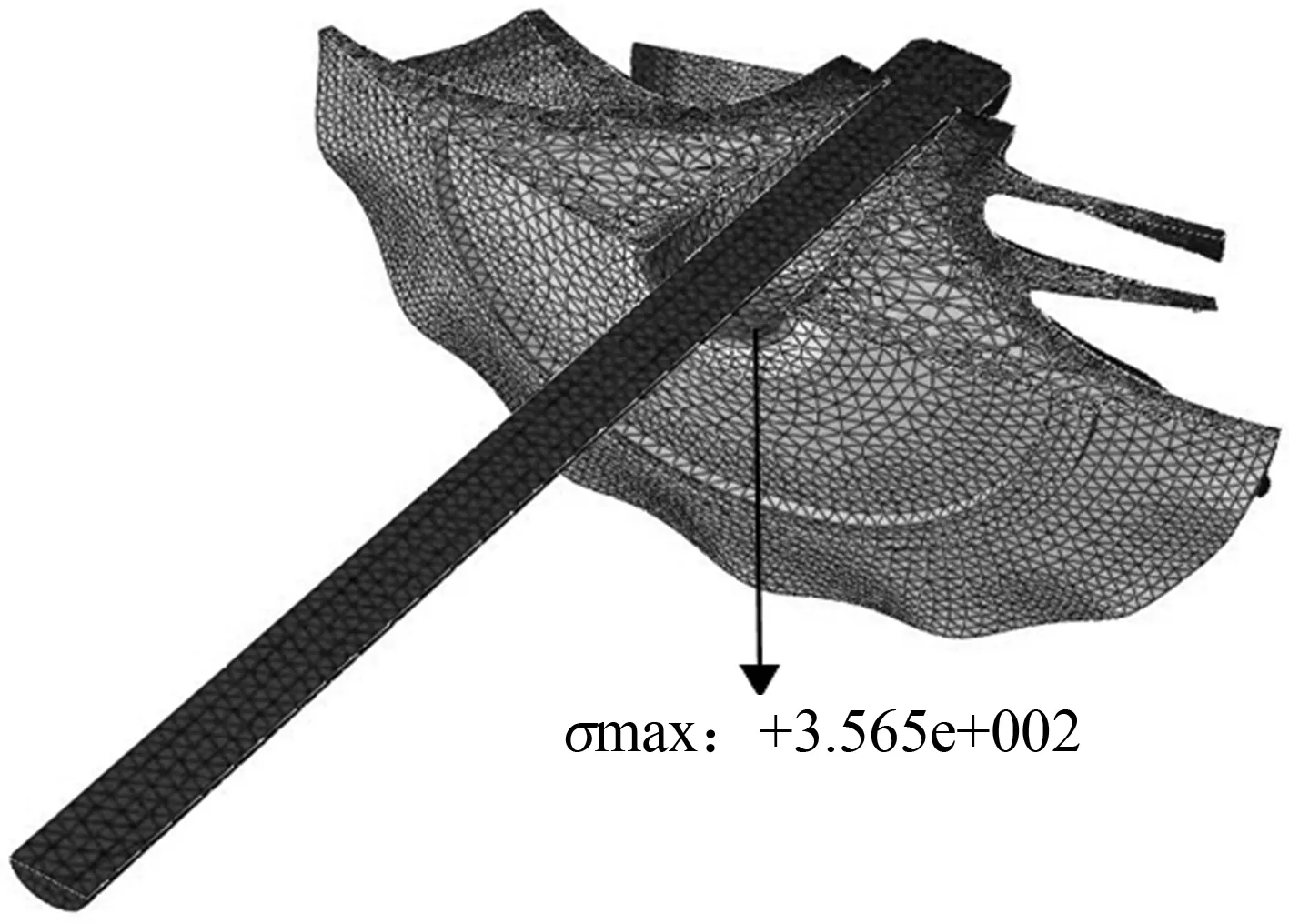
图6 叶轮整体在5种转速下的Mises应力图

叶轮整体的最大Mises应力随转速变化的规律曲线如图7所示.

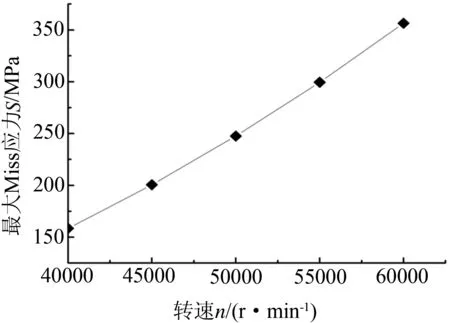
图7 叶轮整体的最大Mises应力随转速变化的规律曲线

从图6可以看出，叶轮内孔底部和叶片根部应力较大，其中最大的Mises应力值均出现在沿轴线方向上的叶轮内孔尾端区域，这是由于叶轮高速旋转，产生很大的离心力之故，叶轮边缘处情况刚好与之相反，应力较小.由图7可以看出随转速的增大，压气机叶轮的最大Mises应力也随之增大.

通过以上分析可以发现，转速n=60 000 r/min时，叶轮内孔底部附近产生了塑性变形，而叶轮其他部分仍为弹性，所以之后需要对压气机进行非线性的弹塑性分析.

4 叶轮整体的弹塑性有限元分析

为了提高运行的安全性，近来在增压器叶轮的制造中采用了预超速的方法，即在叶轮制造时对其施加超过额定转速的转速.当叶轮达到预超速的转速时就卸载，由于这时叶轮将保留残余变形，在以后叶轮投入按额定转速的正式运行时，材料的屈服点将被提高.

通常预超速的转速取额定转速的105%～110%，本节对所计算增压器的叶轮取了5种预超速的转速，即n=60 000 r/min，n=61 000 r/min，n=62 000 r/min，n=63 000 r/min，n=64 000 r/min，对它们分别进行弹性和弹塑性分析，模型建立方法、位移边界条件和载荷施加方式都与前述一致.所不同的是进行弹塑性分析时需要在ABAQUS中定义LD7材料的有关数据(即应力应变关系)，因结构的弹塑性计算与材料的本构关系密切相关.

图8为弹性分析和弹塑性分析下求出的叶轮整体的最大位移随转速变化的规律曲线.

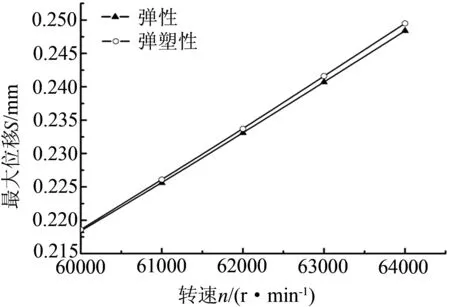
图8 叶轮整体的最大位移随转速变化的规律曲线

由图8可以看出，在弹性与弹塑性分析下，随着转速的增大，叶轮整体的最大位移均随之增大.但比较二者的计算结果可以发现，弹塑性分析下的最大位移值明显高于弹性分析下的位移值，且转速越大，弹塑性分析得到的最大位移值与弹性分析得到的最大位移值之间的差距越大.

弹塑性分析下的叶轮整体在5种超速转速下的最大塑性应变随转速变化的规律曲线如图9所示.

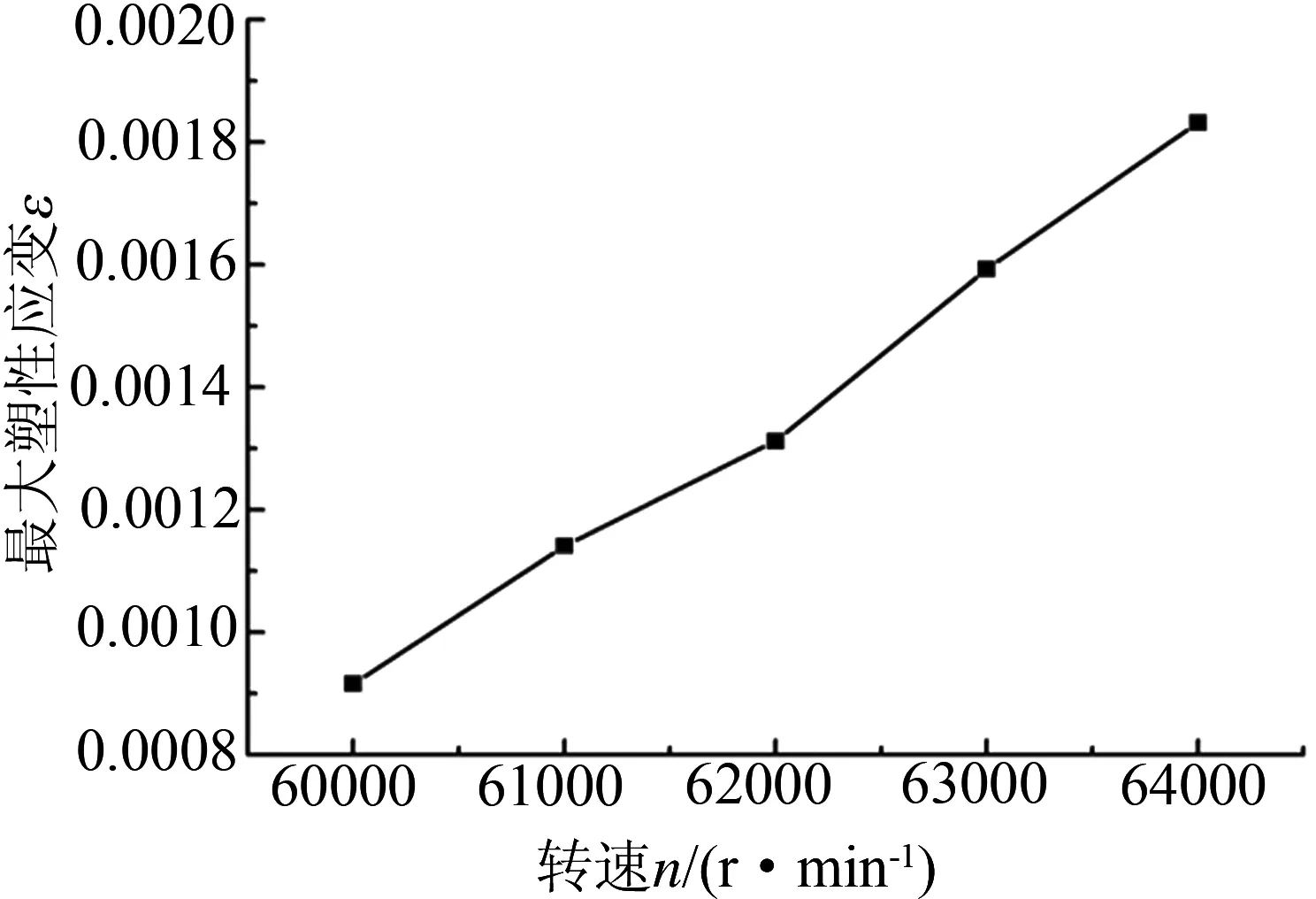
图9 叶轮整体的最大塑性应变随转速变化的规律曲线

图10为弹性分析和弹塑性分析下求出的叶轮整体的最大Mises应力随转速变化的规律曲线.

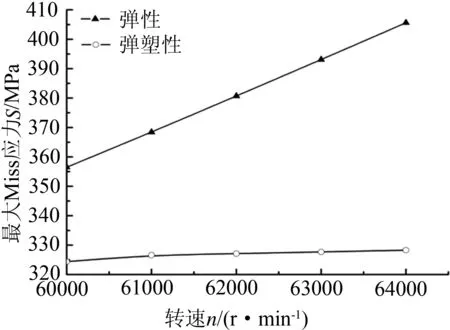
图10 叶轮整体的最大 Mises应力随转速变化的规律曲线

由图9可以看出，随着转速的不断增大，叶轮整体的塑性应变随之增大.由图10可以看出，在弹性与弹塑性分析下，随着转速的增大，叶轮整体的最大Mises应力均随之增大.但比较二者的计算结果可以发现，弹性分析的应力高于弹塑性分析的应力，在预超速转速下，弹性分析的叶轮整体最大Mises应力均远远超过叶轮材料的屈服强度.这是由于叶轮的内孔底部已处于塑性变形阶段，本构关系已经变为非线性的，而弹性分析下的叶轮整体仍然按原来的线性本构关系计算的缘故.对于叶轮整体，各部分产生的变形并不都是弹性变形，弹性变形区与塑性变形区的分界面如何走向，由叶轮在外载荷作用下的总体平衡和内部应变分布相互制约所决定，只有通过弹塑性分析才能计算求出.