压缩感知理论综述与展望
2019-01-03沈益,朱歌
沈 益,朱 歌
(浙江理工大学 理学院,杭州 310018)
0 引言
2003年瑞典卡罗林斯卡医学院授予美国科学家保罗·劳特布尔和英国科学家彼得·曼斯菲尔德生理学或医学奖以表彰他们在核磁共振成像技术领域的突破性成就。磁共振成像仪(见图1)采用磁共振成像(Magnetic Resonance Image,MRI)技术,能够在对身体没有损害的前提下,快速获得患者身体内部结构的高精确度立体图像。它也能用于跟踪患者体内的癌变情况,为更好地治疗癌症奠定基础。磁共振成像仪最终通过计算机系统提供的扫描区域的数字图像,如图2。
数学上用向量x=(x1,x2,…,xn)表示该灰度级图片,其中xi表示对应像素点的值。那么磁共振成像仪是如何获得x的呢?这里暂且抛开原子核旋转,磁场等物理机制,考虑磁共振成像仪中图像的测量与解码。受物理原理的限制,磁共振成像仪并不能直接地,逐点地获得数字图像x,而是通过测量方案获得数字图像的测量信息。假设测量方案为F,测量信息b可表示为

其中F为n×n的矩阵,数字图像和测量信息可具体地表示为
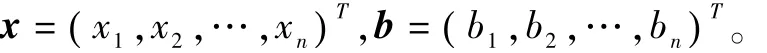
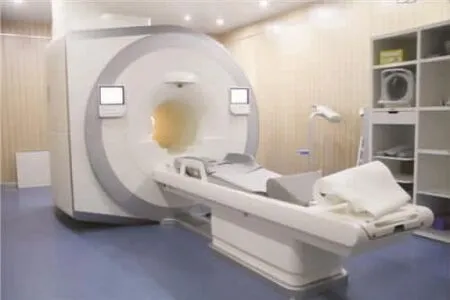
图1 磁共振成像仪

图2 灰度级图像
MRI成像仪所采集到的不是直接的图像像素,而是图像经历过全局傅里叶变换后的数据。因此,(1)式等价于:
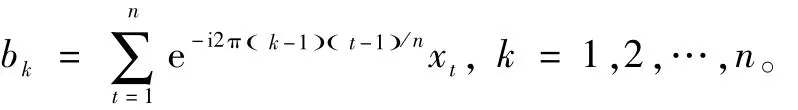
磁共振成像仪内的计算机系统在成像过程中需要求解一个大型线性方程组。传统数学理论指出,当测量获得的数据维度与原始数字图像的维度相同时,通过求解数学模型(1)可以获得精确地原始图像。对于磁共振成像仪,这一求解过程可通过Fourier逆变换实现,如图3。
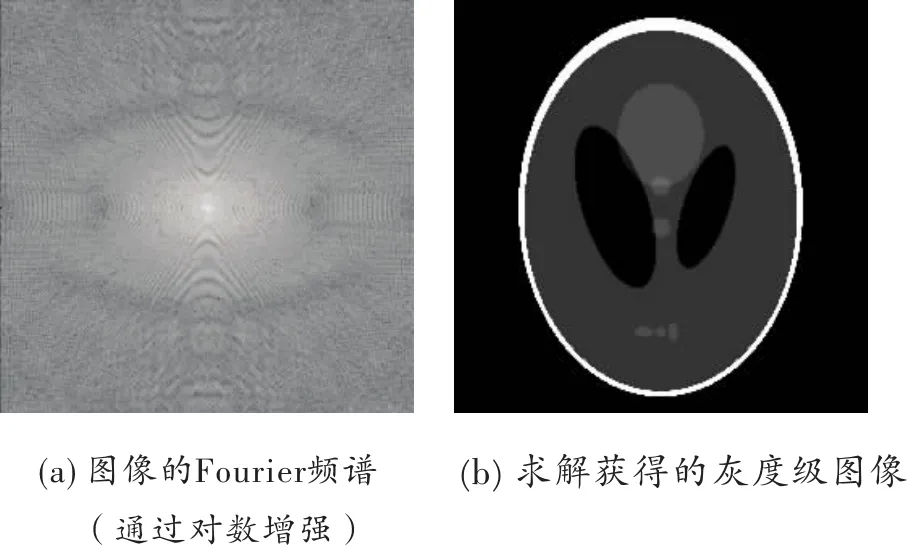
图3 利用 F ourier逆变换恢复信号

图4 利用F ourier 逆变换恢复稀疏信号
但磁共振成像仪在采集数据b的过程中,由于器官运动(如呼吸等非自主运动)或患者自主运动等因素造成图像模糊,此时仅得到图像的部分频谱信息(如图4),采用传统模型和Fourier逆变换方法获得的数字图像不够理想。
对于这样的困难,数学家 David Donoho、Emamnuel Candès、Terence Tao等提出了压缩感知原理[1-4]。这一原理的基本假设为,原始数字图像具有稀疏表示。基于此假设,在信息缺失的情况下,通过求解凸优化模型可以得到实际所需的图像,如图5。
这一理论的发现从数学上几乎完美地解决了信息缺失的问题。该理论极大地缩短了核磁共振成像仪的扫描时间,同时仍能获得等同的数字图像。这样不仅能帮助医生快速做出诊断,也能在单位时间内完成更多病人的检测,给磁共振成像仪带来了新的变革。正是基于这样的数值仿真实验,压缩感知理论一经提出就获得了数学、信息科学、统计学、医学等研究领域的广泛关注。接下来,我们将从数学角度阐述这一理论的基本框架。
1 稀疏信号恢复
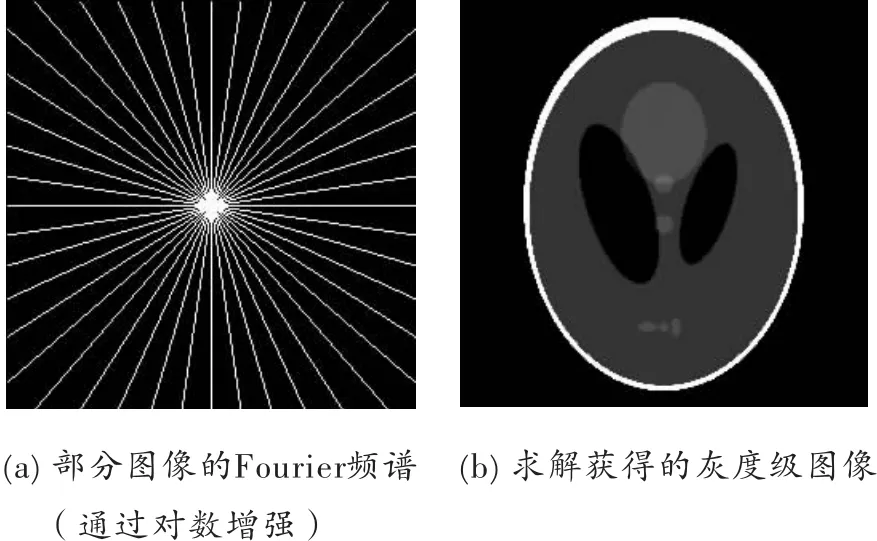
图 求解优化模型恢复稀疏信号5
现实中的信号往往是以时间(例如声音)为变量的连续函数。为了获得离散化数字信号,需要对原始信号进行采样。与传统压缩中先采样后压缩的方式不同,压缩感知并不直接对信号进行采样,而是以线性投影的方式直接获取压缩后的数据,实现信号的编码过程。数学上,这一过程可描述为:假设x为稀疏信号,A为m×n维的测量矩阵(m<n),利用测量矩阵A对稀疏信号x进行投影,得到压缩后的数据b,即

其中,x=( x1,x2,…,xn)T是长度为 n的一维稀疏信号,b=( b1,b2,…,bm)T是长度为m的测量信息。由于m<n,线性方程组(2)的解不唯一。即不能通过测量信息b求得原始信号x。
稀疏性的引入克服了解不唯一的问题。关于稀疏假设的合理性,我们在后面再作介绍。用‖x‖0表示向量x中不为零的分量个数。如果向量中不为零的分量个数‖x‖0不超过s个,则称向量x是s稀疏的。如果测量矩阵的任意2s列是线性无关的,那么该方程组有唯一的s稀疏解。此时(2)式可以转化为求解一个非凸的优化模型

来恢复原始信号。从另一角度看,求解该模型等价于挑选出线性方程组所有可行解中最“稀疏”的解。这种遍历的求解过程使得模型的求解成为一个NP难问题。一个替代方案是通过求解凸的优化模型来恢复原始信号,其中

1.1 测量矩阵
相较于非凸模型(3),凸优化模型(4)的优势在于:可通过凸优化算法快速求解。在数学上,如果一个实际问题可以表示成凸优化问题,那么就认为其能够得到很好的解。在给出两个模型等价性的数学描述之前,先考虑一个简单的几何描述:设

那么线性方程组

的所有可行解在二维平面中为一条直线,如图6所示。在x2轴附近,通过求解模型(3)模型(4)均能得稀疏解

这个例子表明了在二维情况下模型(3)与模型(4)的等价性。
为了讨论高维情况下两个模型的等价性,首先引入集合T⊂ {1,…,n}与其补集 Tc={1,…,n}T。对任意的 n维向量 h,定义n维向量hT满足:hT中第i∈T个分量为hi,第i∈Tc个分量为0。对于s稀疏向量x,记其非零分量的坐标集合为T,则有
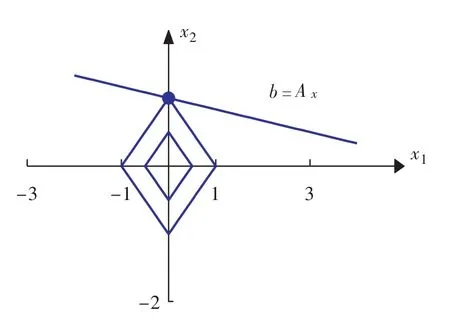
图6 极小化 l1范数稀疏解的几何解释
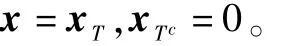
模型(3)与模型(4)的等价性刻画为如下定理:
定理1(零空间性质) 对于任意的s稀疏向量,模型(3)与模型(4)的解相等当且仅当矩阵A满足s阶零空间条件
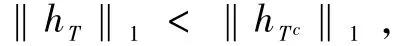
对于任意的#T=s成立。
验证一个测量矩阵A是否满足零空间性质是一个NP难问题。这为测量矩阵的设计带来一定的困难。随机矩阵的引入较完美地解决了这困难。
称矩阵A满足s阶约束等距性质,如果存在正常数δs使得
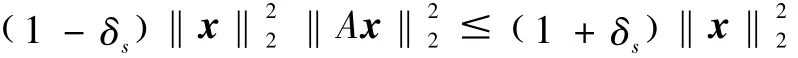
对于任意的‖x‖0≤s成立。正常数δs称为s阶约束等距常数。当 δ2s<1时,若 s稀疏向量 x′,x″均为线性方程组 b=A x的解,则
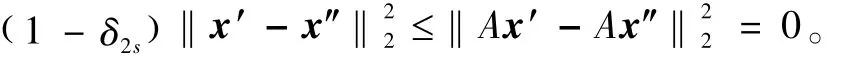
因此,线性方程组b=A x有唯一的s稀疏解。约束等距性质由Emamnuel Candès、Terence Tao首先引入[3],同时他们证明:
定理2[3]如果矩阵A满足约束等距性质且约束等距常数满足

则矩阵A满足零空间条件。
定理2中关于约束等距常数的条件(5)并不是最优的。自2004年定理2的提出以来,很多学者都尝试对这一结果进行改进(改进这一条件并取得了一系列成果)。关于最优界的估计目前已经完全解决,具体可见参考文献[2-3,5]等。定理2另一重要意义在于,很多类型的随机矩阵都满足约束等距性质,如高斯随机矩阵、部分Fourier随机矩阵。
矩阵A称为高斯随机矩阵,如果矩阵A中每一元素ai,j均为独立随机变量且服从均值为0、方差为1/m的高斯分布,即
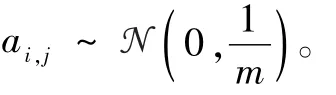
矩阵A称为部分Fourier随机矩阵,如果矩阵的每一行从离散Fourier矩阵

中等概率地随机取得。
定理3[4]当高斯随机矩阵A∈ ℝm×n的行列满足

时,矩阵满足s阶约束等距性质的概率不低于1-e-c(δs)m。
定理4[2]假设部分Fourier随机矩阵A∈ℝm×n测量次数满足m=O( s ln6(n) ) 则测量矩阵A在大概率意义下满足s阶约束等距性质。
注1.当高斯随机矩阵的测量次数满足条件(6)时,通过求解模型(4)可以精确地恢复s稀疏信号[6]。
注2.部分Fourier随机矩阵A∈ℝm×n的测量次数目前被改进为O( s ln4(n) )[7]。很多学者猜测这一测量结果目前还有改进的空间。理想的估计应为O( s ln(n))。
如果向量x为非稀疏信号,取向量中绝对值最大的s个元素,对应的坐标集合记为T,则有
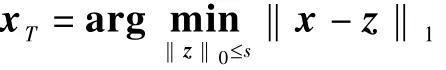
我们称向量xT为向量x的最佳s项非线性逼近。非线性逼近思想在图像压缩中有着重要的作用。当向量的元素按照绝对值从大到小排列后具有多项式的衰减速度,则称这个向量是可压缩的。生活中常见的数字图像的小波系数往往是可压缩的。例如,典型的1 024×2 048数字图像对应一个两百多万维度的小波系数。但通常情况下,约十万个小波系数就足够获取图像所有的可见细节,其余约一百九十万小波系数只贡献少量的、大多数观测者基本看不见的细节信息。这十万个小波系数事实上就是原始小波系数的非线性逼近。目前,微信的图片传输正是采用这样一个数据压缩方案。
定理5[8]假设观测值满足
b=A x+ω,
其中,ω是测量时的噪音,满足‖ω‖2≤η。如果测量矩阵A满足约束等距性质且约束等距常数满足条件(5),则基追踪(basis pursuit)模型

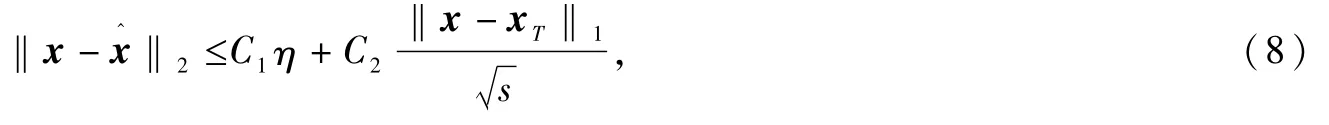
其中,常数C1、C2依赖于约束等距常数。
定理5可以看成定理2在一般情况下的推广,但是两个定理对于约束等距常数的要求没有差别。最优的约束等距常数估计由文献[9-10]给出。如果通过模型恢复的信号x^和原始信号x之间的误差估计满足不等式(8),则称这个模型可以得到稳定解。对于稀疏信号的线性回归问题,基于l1范数的凸优化模型还有Lasso和Danzig Selector[11]等,模型的解也被证明具有类似于不等式(8)的稳定性估计。从凸分析的角度,模型(4)可转化为一个线性规划问题,基追踪模型(7)可转化为一个二阶锥规划问题。两者均可使用相应的优化算法求解。
1.2 非凸模型
基于l1的凸优化模型(4)恢复s稀疏的n维信号,要求测量次数满足m=O(s ln(n/s))。而基于l0的非凸模型(3),理论上要求测量次数满足m=O(s)。因此,两个模型是有着本质的不同的。从理论分析的角度出发,两个模型之间需要建立更多的联系。一个统一的模型是引入lp范数(0<p≤1),信号恢复的模型为

pp很好地刻画了信号的稀疏性。虽然求解Δp问题仍为NP-Hard问题,但是任意一个Δp的解为局部最优解,求解Δp的局部最优解只需多项式时间。因此,相比于求解Δ0,求解Δp拥有更快的计算速度。另一重要原因在于,相比求解Δ1问题,Δp问题可以通过较少的测量次数重构稀疏信号。Chartrand等给出了理论证明[12]:对于由均值为零的独立高斯分布生成的测量矩阵A,测量次数满足
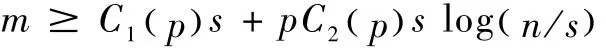
时,Δp问题在概率下有唯一K项稀疏解,其中C1()p、C2()p为常数,并有limp→0pC2()p=0。这一结果从理论上统一了 Δ0、Δp、Δ1中对测量次数的不同要求[13]。随机矩阵满足一定的约束等距性质时,Δp( 0<p<1)模型的最优解是稳定的。模型的稳定性也可以通过随机约束等距矩阵的性质刻画。
定理6[14]对于任意的0<p≤1,如果测量矩阵A满足约束等距性质且约束等距常数满足
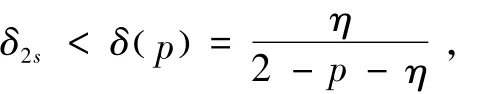
其中,η是方程
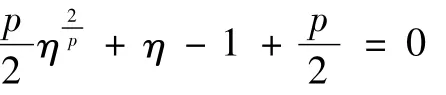
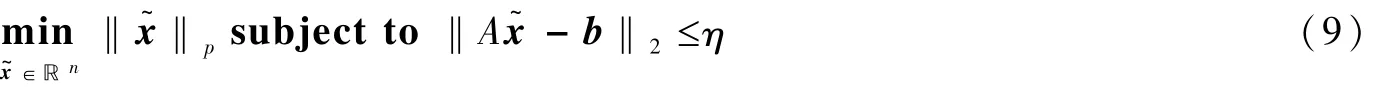
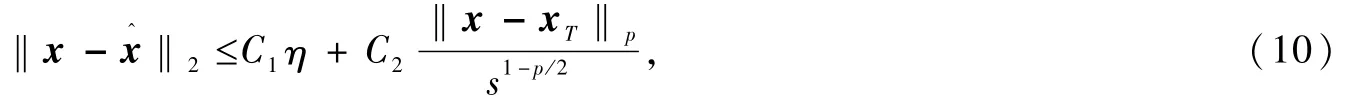
其中,常数C1、C2依赖于约束等距常数。
2 稀疏表示系统-紧框架
压缩感知理论的一个重要假设为:测量的信号为稀疏信号。虽然现实生活中的大多数信号不满足这一假设,但是它们的小波系数往往是可压缩的。对于光滑的信号,最经典也是使用最广泛的紧支集小波(Daubechies正交小波和双正交小波等)具有的消失矩性质保证了其小波系数呈指数衰减。但是对于二维图像的边界特征,特别是光滑的圆弧边界,Daubechies正交小波无法做到稀疏表示。因此 Curvelet[15]、对偶双树复小波[16]等紧小波框架被广泛地应用到图像处理中。相较于正交小波,多方向紧小波框架[17]对二维图像有更稀疏的表达,从而能获得更优的非线性逼近。
给定紧框架小波算子D∈ℝd×n及其共轭转置算子DT,假设信号x在紧小波框架算子D下有稀疏表示c=D x且D T D x=x。理论研究和实验表明:对于非稀疏信号x∈ℝn,测量矩阵A满足一定的条件(例如,E.Candès等提出的D-RIP条件[18]),即使测量次数m小于信号维度n,仍能通过求解带约束的Analysis模型


其中,c1、c2是依赖于D-RIP条件的常数,向量 ( D x)[k]表示向量D x中绝对值最大的k个元素,并将其余元素取为0。针对不同的信号与测量矩阵,需要选择不同的优化模型。特别地,引入紧框架算子后,可选择的模型更加广泛。D-RIP条件的成立并不依赖于紧框架,但在给定测量矩阵的情况下,能否找到合适的紧框架使得信号在该紧框架下具有稀疏表示会直接影响信号的恢复程度。紧框架的引入不仅使得压缩感知理论被更广泛地应用到实际问题中,同时也推动了理论本身的发展。目前对于Analysis模型及其衍生的优化模型的研究最为广泛。为方便求解,大多数算法先将模型转化为无约束形式:

模型(13)称为 ALASSO[19],当测量矩阵 A满足一定的 D-RIP条件时,模型(13)的解是稳定的[19-20]。
如果图像或信号由几类性质相异的成分组成,如由不同乐器奏成的音乐,由神经元的胞体、枝晶、脊柱组成的神经生物学图像等。例如图7中分解为Cartoon部分xc和Texture部分xt的数字图像,其中,Cartoon部分在紧小波框架表示下是稀疏的,Texture部分在局部余弦变换下是稀疏的[21-22]。

图7 分解为 C artoon与 T exture成分的数字图像
对于这种结构复杂的图像或信号,需要采用两个或两个以上的紧框架建立恢复图像的优化模型,例如

E.Candès等针对压缩感知问题提出了该模型[18]。该模型最早称为形态学成分分析(morphological component analysis,MCA),用于分解图像Cartoon和Texture两类成分。模型的稳定性分析见文献[23]。不同之处在于MCA方法中算子A为恒等矩阵,而压缩感知问题中算子A为欠定矩阵。
3 正交匹配算法
最后介绍正交匹配算法(Orthogonal Matching Pursuit,OMP)[24]。OMP算法的基本思想为在每次迭代中选取一个指标作为稀疏信号非零元素的坐标。对于s稀疏信号,正交匹配算法一个自然的停止准则是在迭代s次后停止。每次迭代时,OMP算法实际上是将所选测量矩阵的列依次进行Schimidt正交化,然后将待分解信号减去正交化后矩阵列上的对应分量,得到残差。算法的提出可以追溯到1993年Mallat等学者的工作[25]。2004年,Tropp将 OMP算法成功地引入压缩感知领域中[26]。当测量矩阵的约束等距常数满足时(此上界为最优估计),OMP可在s步迭代后精确地恢复k稀疏信号[27]。即当时,存在确定的测量矩阵使得OMP无法准确地选取信号非零元素的坐标[5]。正交匹配算法没有参数选择的需求,易实现且计算复杂度不高,因此被广泛应用到图像压缩、去噪、字典学习等问题中[28]。稀疏表示是字典学习的核心思想。确定的字典包括小波基、冗余紧框架、Gabor框架等。确定字典的基本假设是信号可以由字典中的一个或几个元素表示。但是给定的字典总是具有局限性,例如在小波分析中,一般假设信号具有一定的光滑性。另一种选择字典的方法是自适应的,字典学习考虑从数据本身出发,通过一定的方法,例如求解优化模型,构造适用于该数据或类似数据的表示系统。
4 总结与展望
压缩感知恢复信号的方式是通过各种优化方法从压缩测量中恢复原始信号。当原始信号稀疏或可压缩时,且测量矩阵满足一定条件,可通过求解凸优化模型高概率地恢复原始信号。当原始信号不稀疏,但在某组基或某组框架下可以得到信号的稀疏表达时,且测量矩阵满足一定条件,通过求解凸优化模型可以得到稳定解。理论上,基于RIP条件的稳定性分析的相关理论目前已经取得较为完善的理论结果。在应用上,压缩感知理论已经取得了标志性的工业成果 Donoho,From Blackboard to Bedside:High-dimensional Geometry is Transforming the MRI Industry。
受压缩感知理论的启发,其他相关研究课题的理论成果及其应用,例如低秩矩阵恢复、相位恢复、1-bit压缩感知、超分辨分析、盲去卷积等也取得了较大的突破。压缩感知理论系统地阐述数据的稀疏表示与恢复及其相关理论,L1范数的引入使得基于稀疏表示的数学建模具备了非常广泛的应用前景和理论支撑。特别是在人工智能,深度学习等领域,例如,稀疏自编码直接把多个单层基于压缩感知的稀疏编码机叠加在一起形成了一个深度学习的模型。如何将压缩感知这一研究领域的理论成果应用到深度学习中,解释深度学习的数学机制,是一个广阔的研究方向。
致谢:论文在浙江大学李松教授的建议及鼓励下完成,在此表示感谢。
