一类非紧集的拓扑压的变分原理

王 威

（南京审计大学 金审学院基础部，南京 210023）

0 引 言

设M（X）是X上所有的Borel概率测度集。M（X，T）⊆M（T）是所有T-不变的概率测度集。设Z⊆X为T-不变集。E（X，T）⊆ M（X，T）为遍历测度集，且满足 μ（Z）＝1，∀μ∈ E（X，T），对于 x∈ X，定义概率测度

εn（x）的极限点集用 V（x）表示，则 V（x）⊂ M（X，T）。

非紧集合的拓扑压的变分原理：若V（x）∩E（Z，T）≠Ø，∀x∈Z，则对任意实值连续函数φ：X→R，有

若φ＝0，即为非紧集的拓扑熵的变分原理。若Z为紧致集合，则与经典变分原理一致。对于非可加的情况Falconer［1］在混合排斥子上建立了次可加的变分原理，Barreira［2］介绍了紧致度量空间的任意非可加的变分原理，这个变分原理推广了Pesin和Pitskel［3］在可加条件下关于非紧集合的变分原理。Murmmert［4］给出了几乎可加的变分原理，曹永罗等人［5］定义了次可加序列拓扑压，并建立了不在任何假定可加条件下的变分原理。2009年和2012年丰德军和黄文［6-7］定义了极限次可加函数并且给出了极限次可加函数序列下熵的变分原理，2013年曹永罗［8］等给出不可加性质下压的应用。丰德军和黄文此后讨论了加权压的遍分原理［9］，近年amenable群上的通游点的拓扑压的遍分原理也得到了证明［10］。由此想到是不是在这种特殊的非紧集合上它的压的变分原理也成立，本文就在此基础上进行了研究。

1 预备知识

定义1设 （X，T）是 TDS，F＝｛fn｝∞n＝1是定义在X上一列连续实函数。设U是X的有限开覆盖定义

给定A∈Wn( T，U)且A≠ Ø，集合mT(A)＝n，FT(A)＝(x)。若 A＝Ø，则 mT(A) ＝0，FT(A) ＝-∞对每个集合Z∈X和每个实数s，定义

其中 PZ（T，U，n）是所有有限或可数的覆盖 Z的 Γ的集合，且 Γ⊂∪k≥nWk（T，U），很显然 MZ（T，s，F，U，n）是关于n的单调递增函数，设

更进一步，定义：

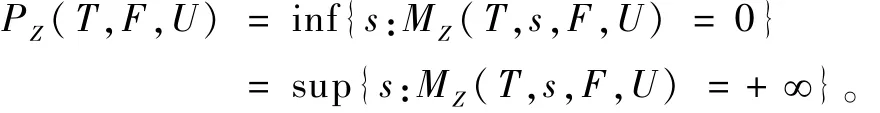
若 X的开覆盖 U，V，且 U≥ V，则 PZ（T，F，U）≥ PZ（T，F，V）。

记

称PZ（T，F）为F在集合Z上的关于T的拓扑压，其中定义中的Z不必是紧的或是不变的。

定义2设 （X，T）是 TDS，F＝｛fn∈C（X，R）∞。称 F是次可加的，如果对任意 n，m∈N和 x∈X，有 fn+m（x）≤ fn（x）+fm（Tnx）。

定义3 设 （X，T）是 TDS，F∈ C（X，R）∞。我们称 F是极限次可加的，如果 ［F］∈ Ψs（X，R，T）。

注1由定义3容易验证，F相对于T是极限次可加的，当且仅当存在 ｛Fi｝⊆ C（X，R，T）∞s，使得

定义4设 （X，T）是 TDS，F＝｛fn｝∈ C（X，R）∞，则 F上的上 Lyapunov指数 λF（x）定义为：

函数列 F诱导出映射F*：M（X，T）→R∪｛±∞｝定义为：

定义

更进一步，对任意的α∈R，定义：

本文主要研究集合 EF（α）上拓扑压 PEF（α）（T，α）。

2 主要定理及证明

定理1 （非紧压的变分原理）设 （X，T）是TDS，F＝｛fn｝∞n＝1是 （X，T）上的极限次可加连续函数列，φ∈ C（X，R），则

（1）若 μ∈Me（X，T）且F*(μ)＝α，则

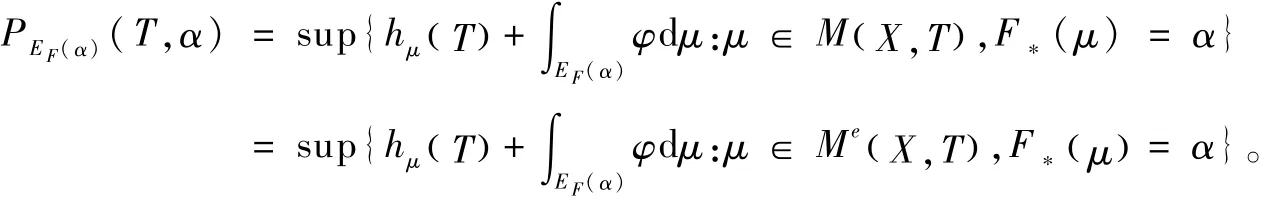
要证明定理1需要以下几个引理和命题。

对h≥0，考虑集合

引理 1［9］对于 h≥ 0，有

设 （X，T）是 TDS，u＝｛u1，u2，…，ur｝∈，ε＞0，m∈ N，记

引理2［9］设x∈X，μ∈V（x），u是X的有限开覆盖，对于ε＞0，存在实数m＞0和充分大的数n，使得 L＞n，t∈ ｛1，2，…，r｝L，满足：

(2) SLφ（u）≤ L(∫φd u+r(u)+ε)；

(3) t包含一个长度为—t ＝Km＞L-m的子链—a，即a＝(a0，a1，…，aK-1) ∈（u），满足：

引理 3［6］若定义，则

（1）（F）∈ R∪ ｛-∞｝；

（3）下列条件等价

（b）λF()x ＝-∞对 ∀x∈ X，

（c）F*（μ）＝-∞对∀μ∈M X，()T，

（d）PXT，()F＝-∞；

引理 4［6］设 （X，T）是 TDS，F＝｛fn｝是定义在 （X，T）上的极限次可加函数列。假设 ｛νn｝∈M()X 。令构造一个新列 ｛μn｝∞n＝1。假设在 M()X 中，当 ni→+∞时，μni→ μ，则 μ∈M X，()T，而且

引理 5［6］设 （X，T）是 TDS，F＝｛fn｝是定义在（X，T）上的极限次可加连续函数列，则

（1）对于μ∈M X，()T；

（2）F*：M X，()T→R∪｛-∞｝是上半连续的，并且存在C∈R，对所有的μ∈M X，()T，使得F*()μ≤C；

（3）设 μ＝∫Ωθd m（θ）是μ∈M X，()T的遍历分解，则

（4）对μ∈M X，()T，μ-a．e x∈X，λF()x存在，并且存在C＞0，使得λF()x≤C和F*()μ＝。特别地，当μ∈MeX，()T时，对，μ-a．e x∈X，有λF()x＝F*()μ。

命题 1［3］设 （X，T）是 TDS，Z∈ X是 T-不变集，对任意的 x∈ Z，V（x）∩ M（Z）≠ φ，且 μ（Z）＝1，φ∈C X，()R有

命题2 设 （X，T）是 TDS，F＝｛fn｝∞n＝1是定义在（X，T）上的极限次可加连续函数列，φ∈C X，()R，若＝α，则

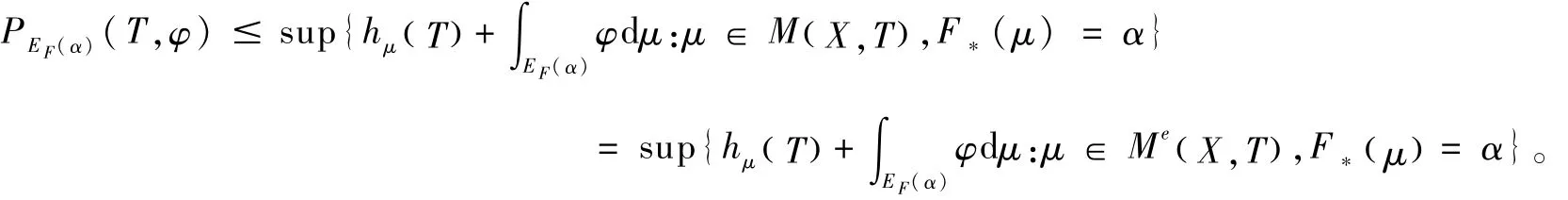
证明首先证明

只须证明

设μ∈M（X，T），且F*()μ＝α，μ＝F*()θd m()θ为μ的遍历分解。由引理5（3）知α＝F*()μ＝＝1其中 Ω ＝｛θ∈Me( X，T)：F*(θ)＝α｝。所以

所以

相反的不等式显然成立。所以命题中等式成立。

所以有

所以结论显然成立。

假设C＜+∞，否则，若C＝+∞，则命题显然成立。

设u＝｛u1，u2，…，ur｝∈，ε＞0，对于x∈EF()α，μ∈V（x），存在ni→+∞，使得

又由引理3（2）知α＝F*()μ，所以

由引理 2知，存在一个数 m ＞0和 n＞0，满足：（1），（2），（3）。

用Km表示集合｛x：x∈EF()α｝，使得对任意的n＞0，有L＞n，t∈｛1，2，…，r｝L，满足：

(1)mx∈T-iut(i) ；

(2)mSLφ（—u）≤L(∫φd u+r(u)+ε)；

(3)mt包含一个长度为—t＝Km＞L-m的子链—a，即a＝(a0，a1，…，aK-1) ∈（u），满足：

显然可知 Km＝EF(α)。

用Km，l表示集合x∈Km，使得对某一 μ∈M( X，T)，满足：(1)m，(2)m，(3)m且φdμ∈ ［l-ε，l+ε］，对于 x∈ Km，l，则

选取 λ＞C+4ε+r()u ，固定 m，l，对 L≥1，设 Sm，l，L表示所有 t∈ ｛1，2，…，r｝L的集合，使得存在 x∈Km，l，满足：（1）m，（2）m，（3）m。对t∈Sm，l，L，相应的子链a—包含在R（K，m（C-l+2ε），Em（u）中。其中L≥mK≥L-m，所以

由引理1，可得：

设L0≥N，因为∈ ΓK，l（T，U，L0）（其中 ΓK，l（T，U，L0）为 Km，l的覆盖）。

所以有

其中 β＝eC-λ+4ε+r（u）＜1。

当 L0充分大时，MKm，l( T，λ，φ，U)＝0。所以对 ∀m，lλ≥PKm，l( T，φ，U)都成立。所以

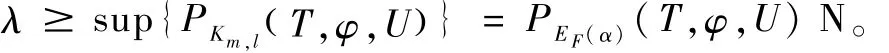
进而有 C+4ε+r（u）≥ PEF（α）（T，φ，U）。

令 r(u)→ 0，ε→ 0，l→ 0，则有 C≥ PEF（α）（T，φ，U）。即

定理1的证明

证明

（1）设 μ∈Me（X，T），且F*(μ)＝α，由引理5的（4）知，对 μ-a．e，x∈X有F*(μ)＝λF(x)，所以μ( EF(α) ) ＝1。又

由命题1知PEF()α（T，φ）≥hμ（T）+∫EF()αφdμ。

3 定理的推论及应用

则

应用前面的结论，我们可以推得以下结论：

推论1 若 （X，T）是TDS，F＝是 （X，T）上的极限次可加连续函数列，φ∈C（X，R），α＝β_（F）

由BS-维数的定义可以推得以下的结论。

推论2 若 （X，d，T）满足 g-几乎乘积性质，则

推论3 设Cr黎曼流形X是一个扩张的且拓扑混合的C1+δ共形映射T的排斥子， 则

Barreira和 Saussol在文献［11］中证明了，若测度熵满足上半连续条件，Ø，ψ有唯一的平衡态，则BS-维数也满足推论1中的结论。