基于干涉法的非球面测量技术
2019-01-03郝群宁妍胡摇
郝群,宁妍,胡摇
(精密光电测试仪器及技术北京市重点实验室,北京理工大学 光电学院,北京 100081)
0 引言
非球面是对偏离球面的曲面的总称。在光学系统中使用非球面光学元件,不仅能增加光学设计的自由度,有利于像差校正、改善像质、提高光学系统性能,而且能够减少光学元件的数量和重量,简化仪器结构,大大减少系统的尺寸和重量,降低成本[1]。
基于非球面光学元件的上述优点,很多光学系统中已经广泛使用非球面替代球面光学元件,成为起支撑作用的关键部件。小到普通的眼镜镜片,大到照相透镜、平版印刷系统、天文望远镜等复杂的光学系统,特别在航天领域,成像系统追求的小体积、轻重量和高成像质量,使用球面元件是难以实现的。
2002年5月,在欧洲航天局提出的“COSMIC VISION”空间天文学计划中,研制的Herschel望远镜主反射镜是直径为3.5 m的凹面抛物面镜,次镜为直径308 mm的凸面双曲面镜。在美国NASA与德国航空局DLR的联合项目SOFIA(Stratospheric Observatory For Infrared Astronomy)中,使用凸非球面与其所属的望远镜系统一起,作为航空侦察和临近空间侦查相机的关键部件。计划2018年发射的用于太空探测的JWST(James Webb Space Telescope)望远镜采用凸双曲面作为次镜。
我国对于非球面在空间遥感光学系统、天文望远镜等领域中的应用,也开展了相关研究工作。云南丽江高美古天文台投入使用的“2.4MR-C望远系统”,它的主镜和副镜分别是四凸旋转双曲面镜。在航天遥感领域,从上世纪90年代开始,长春光机所的杨晓飞、韩昌元等人研制装调的口径600 mm、焦距6000 mm、视场3°离轴三反射镜光学系统、中国科学院南京天文光学技术研究所的研究人员装调的口径为250 mm的离轴卡塞格林系统、中科院西安光机所研制的基于共轴三反光学系统的长焦距高分辨力空间相机均是将非球面应用到空间遥感光学系统的成功案例[2]。此外,2010年8月发射的天绘一号、2012年1月发射的资源三号卫星、2013年4月发射的高分一号卫星、2014年8月发射的高分二号卫星、FSW系列返回式卫星,十二五期间研制和发射的一系列后继卫星,均在遥感卫星平台上使用了非球面光学元件。但由于非球面检测的困难,使得非球面的加工精度一直不能够得到保证,研究高精度、简单实用的非球面检测技术,目前还是光学检测领域的一大难题[3]。
非球面光学元件的加工方法很多,其中应用最多的是适用于加工高精度、大口径、深度非球面的去除加工法。非球面去除加工法的工艺过程主要分为研磨、粗抛光和精密抛光三个阶段,各阶段的面形加工精度依次提高,检测方法也有所不同[4]。
在研磨期,非球面与其理论面形的偏差很大,一般采用普通的接触式轮廓仪对其面形进行初步检测。在研磨后期以及粗抛光阶段,非球面表面与理想面形之间仍存在较大偏差,但接触式轮廓仪等方法由于容易划伤元件表面,且精度受限,已无法满足加工要求。同时,由于此时非球面元件表面的反射率较低,因此可以利用激光跟踪仪或非接触式Shack-Hartmann波前传感器法、Ronchi光栅法等对其面形进行测量。精密抛光阶段的非球面表面光滑,具有较好的反射率,其与理论面形之间的误差较小,主要采用非接触的干涉法进行面形检测。
干涉法作为非球面最终的加工检测方法,具有灵敏度高、测量准确度高、可实现非接触测量等优点,是非球面高精度面形误差检测的重要方法,应用十分广泛。干涉测量法根据测量原理分为零位检验法与非零位检验法,本文将对其进行详细介绍。
1 零位检验法
零位检验法的基本思想[5]指的是,当被测镜为理想非球面且检测系统理想装调时,测试光束经过被测镜后能够原路返回,与参考光束发生干涉后产生“均匀一片色”的零条纹或等间距直条纹。而当被测镜是理想非球面镜时,按照零位条件,为了使测试光束经被测非球面后能够原路返回,需要在检测系统中使用特殊的补偿光学元件,使干涉仪出射的平面波或球面波转换成与被测理想非球面面形一致的非球面波,以补偿被测非球面像差。在检测实际的非球面时,根据实际干涉条纹与理想干涉条纹之间的偏差,可以得到被测非球面的面形误差。下面将重点分析零检验法中常用的无像差点法及补偿镜法测量非球面的面形误差。
1.1 无像差点法
在非球面的检测中,干涉仪只能出射平面波前或者球面波前,不能直接用于非球面的检测。但二次曲面不同于其它非球面,其几何焦点是一对共轭的无像差点,即二次曲面的几何焦点,满足“点物成点像”的光学共轭成像条件[6]。
因此,在二次曲面的检测中,可以设置干涉仪标准镜为球面标准镜,使其发出的球面波的焦点,与二次曲面的一个共轭点重合;干涉仪发出的球面波经二次曲面第一个共轭点可无像差的成像在其第二个共轭点处,在二次曲面第二个共轭点处放置一个曲率中心与该共轭点重合的平面或球面,便可实现无需其它辅助元件的无像差点检测[7]。
以抛物面的检测为例,如图1所示,令干涉仪发出的球面波焦点与待测抛物面焦点重合,并在抛物面焦点附近放置一中心带孔的辅助平面镜,则位于抛物面焦点的点光源发出的光经待测抛物面反射后便形成平行光;当该平行光到达辅助平面镜后便可原路返回,从而形成零位检测。
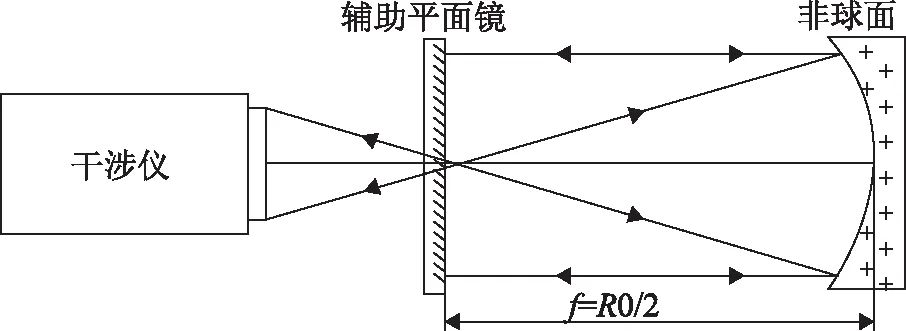
图1 无像差点法检测抛物面示意图
无像差点法是一种常见的二次曲面检测方法,检测装置简单,一定程度上可以实现二次曲面的通用化检测。但此方法存在几点不足:首先,对于不同的二次曲面,通常需要不同的检测光路,适用的辅助镜也会不同,并且检测结果极大地依赖于辅助镜的面形精度;其次,辅助镜中心需开孔,无法同时完成二次曲面的全口径测量,且辅助镜的口径要大于被测二次曲面,尤其在凸面检测中,辅助镜的口径往往是被测镜的几倍,极大的增加了光学检测装置的成本;最后,在实际应用中,无像差点法的检测常常会受到光路长度的限制。
1.2 零位补偿法
补偿法的基本思想是根据待测非球面的光学参数,设计并加工补偿器,将干涉仪发出的平面波前或球面波前转化为与待测非球面匹配的非球面波前。
零位补偿法是指在检测系统中引入的辅助光学元件,即零位补偿器,把干涉仪出射的平面波前或球面波前转换成与待测非球面理论形状完全重合的非球面波前,使得测试光束到达待测非球面后能够原路返回。补偿器按照光学性质可分为折射、反射、衍射零位补偿器。本节将根据补偿器光学性质的不同,介绍几种常见的零位补偿法。
1.2.1折射零位补偿器
折射式零位补偿器是利用折射式光学元件来补偿待测非球面的像差。在三种不同光学性质补偿器中,折射式补偿器发展比较成熟。本节将介绍两种典型的折射式零位补偿器,Dall补偿器与Offner折射补偿器。
已知透镜的球差是其共轭距的函数,如图2所示[8],采用单块平凸透镜,通过适当的选择补偿镜共轭距,对小口径抛物面镜的像差进行补偿。单透镜的球差随其共轭位置的改变而改变,因此同一个平凸透镜可以用作多个抛物面镜像差的补偿。
Dall补偿器属于单光路补偿,由于检测光路不对称,在检测过程中会导致彗差的引入;此外,在Dall补偿器检测光路中,光线仅一次通过补偿器,因此,补偿器需要承担两倍于待测非球面的偏离量,仅适合于小口径、小非球面度的检测。
Offner补偿器由补偿镜和场镜组成,单独的补偿镜只能校正待测非球面的初级球差,在补偿镜后设置场镜,可将补偿镜成像至待测非球面处补偿非球面的高级球差。图3所示为一个通过场镜把补偿镜成像在待测非球面上的Offner补偿光路[8]。
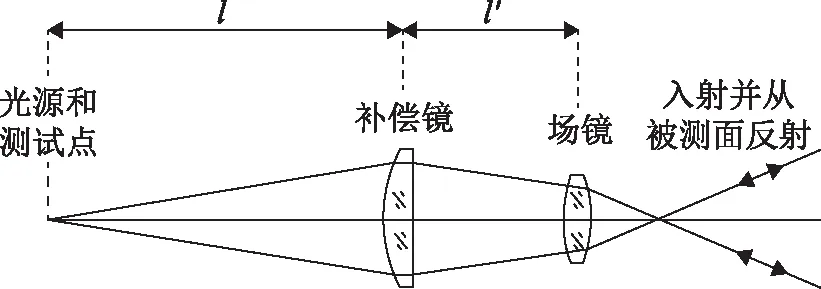
图3 折射式Offner补偿器
1.2.2反射零位补偿器
折射式补偿器的缺点是受材料折射率不均匀性的影响,各个补偿元件的折射率偏差难以达到预期的精度。在测试光线两次通过补偿镜的情况下,微小的折射率偏差会引起较大的光程差。随着待检非球面口径的增大,需要的补偿元件的口径和厚度也随之增大,透镜折射率偏差对测量精度的影响也越大。为了解决这一问题,可以采用反射式光学元件补偿非球面像差[9]。
以下将介绍两种典型的反射式offner补偿光路。
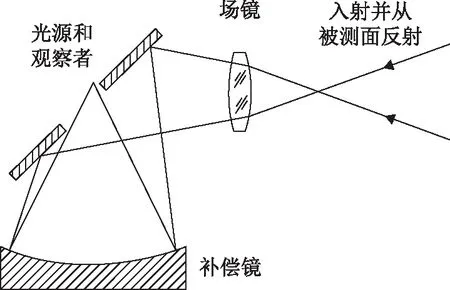
图4 单反射镜Offner补偿器
图5为带有场镜的双反射式Offner补偿器检测光路。由于补偿器中心开孔,所以无法实现待测非球面全口径面形误差的检测。
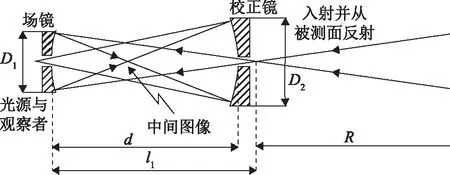
图5 带有场镜的双反射镜Offner补偿器
1.2.3衍射零位补偿器
衍射补偿器主要是指应用衍射光学元件——计算全息图(Computer Generated Hologram,CGH)作为非球面检测系统的补偿装置。计算全息是指通过数学计算的方法,根据待检非球面的数学模型,计算出与其匹配的非球面波前,并利用计算机生成能够产生该波前的全息图。计算全息法的常见光路结构有两种CGH,分别位于观察空间和检测空间。如图6所示为CGH位于观察空间的光路结构[8]。参考光束与携带待检非球面面形误差信息的测试光束经过CGH均会发生衍射,通过倾斜参考镜,选择合适的衍射级次发生干涉,如测试光束的0级衍射波前与参考光束的+1级衍射波前发生干涉,或者测试光束的-1级衍射波前与参考光束的0级衍射波前发生干涉。根据采集到的干涉条纹,即可解算出待测非球面的面形误差。在此光路结构中,参考光束和测试光束均同时通过CGH,对全息图存储基底的均匀性要求较低。

图6 使用CGH补偿器的泰曼格林干涉仪
图7为CGH位于检测空间的光路结构,在此光路中,参考光束不经过CGH而测试光束两次经过CGH,因此对全息图存储基底的均匀性要求较高,增大了CGH的加工难度。
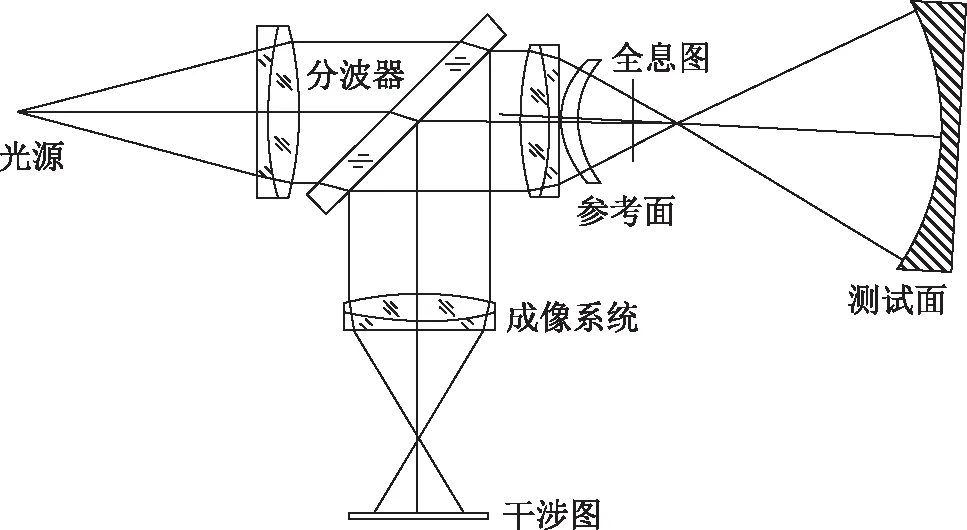
图7 使用CGH补偿器的菲索干涉仪
图8为双CGH检测凸非球面的系统示意图[10]。该系统基于菲索干涉原理,在光路前一部分放置两片CGH。检测时,激光器发出的激光经准直系统后平行入射,通过第一片CGH,取第一片CGH的1级衍射光,此级衍射光通过第二片CGH,取第二片CGH的0级衍射光,定义此级衍射光从照明系统最后一面,即参考球面返回的光为参考光束;定义第二片CGH产生的1级衍射光经照明系统入射到待测非球面并返回的光束为测试光束。在此系统中,第一片CGH的1级衍射光补偿参考波前的像差,同时补偿测试波前的部分像差;第二片CGH的1级衍射光补偿测试光束的剩余像差。在这个系统中,在待测非球面前放置照明镜参考球面是为了使光直接照射到待测非球面上,从而克服待测镜折射率不均匀性对面形检测精度的影响。此系统中参考光和检测光基本是共路的,因此抗干扰能力强,对共路部分元件的要求也相对较低。两个 CGH 只是小口径的平面 CGH,同时参考球面的尺寸只需比待测镜稍微大一点即可,不需要传统检测凸非球面时所用的尺寸大几倍的辅助球面镜。另外,此方法还可以检测离轴非球面和自由曲面。但在检测过程中,要得到更好的干涉图,就要确保系统中两束光能够汇聚为同一点,同时还需要用空间滤波器滤掉其他的干扰级次。
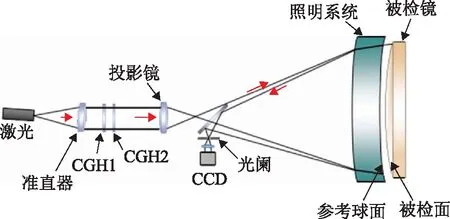
图8 双CGH检测凸非球面示意图
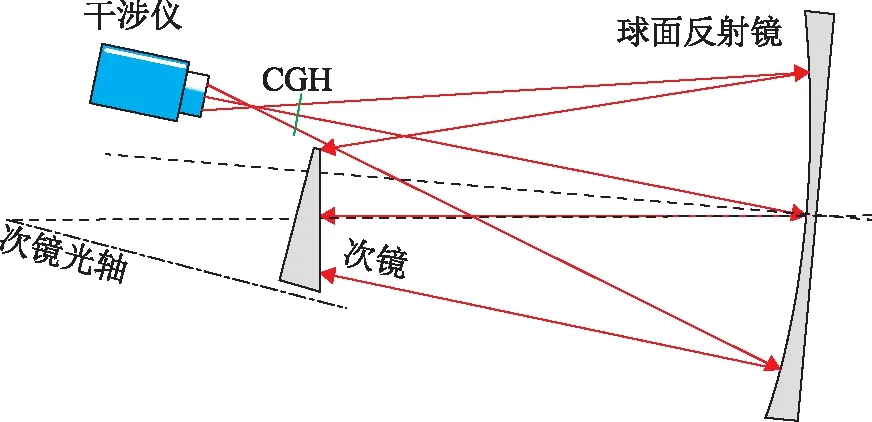
图9 CGH与球面反射镜混合补偿
以上介绍了几种使用单一CGH补偿器检测非球面的检测系统,但对于大口径大偏离量非球面及较大口径凸非球面,由于 CGH制作上的尺寸限制和条纹密度限制,难以单独使用 CGH完成补偿,需采用混合补偿方法检测。本节将继续介绍 CGH与辅助元件混合补偿检测非球面的方法。
图9为CGH与球面反射镜混合补偿的离轴检测系统[11]。由于离轴非球面的偏离量主要来源于像散和彗差,因此,光路中通过使用倾斜的球面反射镜,产生较大口径的汇聚光波前,引入一定的离轴误差,一定程度上补偿待测凸非球面的像散和彗差,利用CGH补偿非球面固有像差、球面反射镜引入的球差、离轴使用球面反射镜引入的非对称像差等系统剩余像差。借助球面反射镜与CGH一起完成待测非球面波前的零位补偿,以此降低大偏离量大口径离轴非球面检测中CGH补偿器的补偿难度。
从表5可以看出,锦紫苏种植60 d,除处理⑥的叶片数和最大叶长外,其余各处理组与对照组相比均有极显著差异。处理⑥和处理⑦各项指标均处于同一水平,略低于对照组⑧。所以处理⑥的各项指标与对照组接近。从图1可以看出,处理⑥植株优美,长势较好,具有良好的观赏性。因此,认为处理⑥的栽培基质与对照组⑧对锦紫苏的生长影响基本一致。
与折射反射式补偿器相比,CGH补偿器结构简单,易于装调,且能够生成任意形状的波前,理论上适合所有类型的非球面面形误差检测。但对于相对孔径大且非球面度较大的非球面,与其匹配的全息图刻线非常密集,难以实现该全息图的加工。
本节介绍了几种常见的零补偿法。零补偿法具有很高的检测精度,但零补偿器往往结构比较复杂,加工制造成本高、难度大,且针对性很强,一种补偿器只能用于一种特定参数的非球面面形误差的检测,通用性不强。
2 非零位检验法
与零位检验法相比,非零位检验法在检测非球面时,即使待测非球面没有面形误差,且检测系统理想装调,干涉仪出射的光束经过待测非球面仍不能原路返回,干涉仪无法探测到零条纹或等间距直条纹。因此,非零位检验法对补偿系统的光学设计要求有所下降,但对系统的机械装调控制、检测算法等提出更高的要求。
2.1 环带拼接法
环带拼接法,指的是在旋转对称非球面的检测中,当待测非球面沿着光轴运动到某一位置时,干涉图上会出现少量可分辨的环状干涉条纹,其测量原理如图10所示,但一个位置的检测结果不能实现待测非球面全口径面形误差的检测。为了得到非球面的完整检测结果,将待测非球面置于干涉仪光轴方向上的多个位置,通过多个位置环状条纹的“拼接”,实现整个非球面的检测。环带拼接法的优点是测量原理简单,但要实现环状条纹的准确拼接,需要准确测量待检非球面的位置,因此在检测装置中往往需要高精度的位移测量装置。
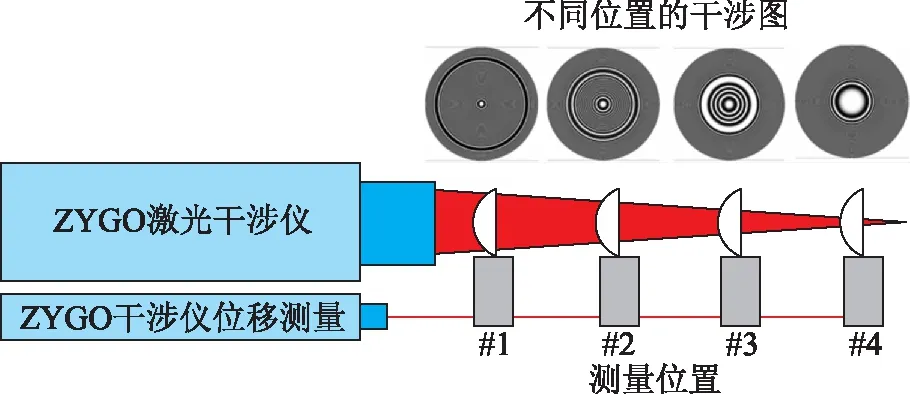
图10 环带拼接法测量原理
2.2 子孔径拼接法
子孔径拼接法[12]与环带拼接法类似,也是将待测非球面口径划分成若干个子孔径进行测量。当干涉仪出射的检测光线波前法线与非球面上被测区域法线重合时,检测光线到达被测区域后能够原路返回,干涉图上该区域出现携带非球面面形误差的近零级干涉条纹,如图11所示;通过精确调整干涉仪与待检非球面的相对位置,可以获得非球面口径上各个子孔径的测量结果[9]。
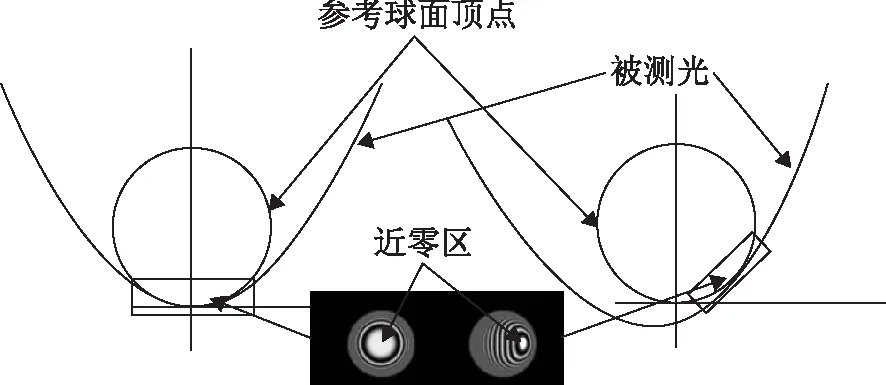
图11 被测区域的近零干涉条纹
根据子孔径形状的不同,常见的子孔径拼接法有环形子孔径拼接法、圆形子孔径拼接法和矩形子孔径拼接法等。图12为椭圆子孔径拼接算法各个子孔径的干涉图样与待测非球面全口径相位恢复结果[13]。通过图像处理算法与子孔径拼接算法将各个子孔径的测量结果拼接可以得到非球面完整的面形误差测量数据。
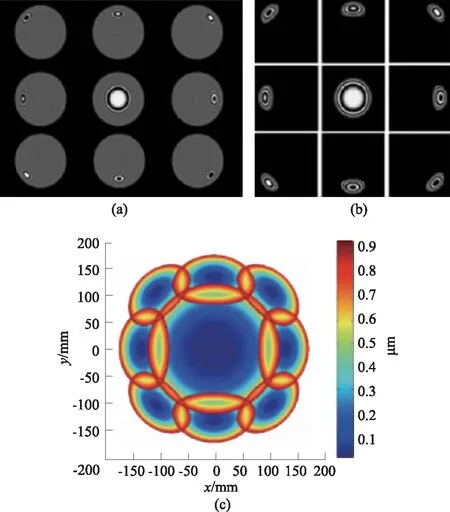
图12 椭圆子孔径拼接法相位恢复结果
子孔径拼接法与环带拼接法的区别在于,环带拼接法中,非球面仅沿光轴方向移动,而子孔径拼接法中,非球面除轴向移动外,还要做倾斜运动与平移运动。
子孔径拼接法的优势在于,不需要借助辅助元件便能实现大口径、大非球面度非球面全口径面形误差的测量,检测精度高,很好的解决了高分辨力与大视场之间的矛盾。但子孔径拼接算法仍存在不足:子孔径拼接算法复杂且耗时,无法用于大口径非球面面形误差的实时检测。此外,测量中要将待检非球面口径划分成若干个子孔径,且各个子孔径之间要有一定重叠区域,因此检测装置的装调与校准存在一定的难度。
2.3 双波长全息法
在传统移相干涉法中,通过反正切函数恢复的相位分布通常都被包裹在(-π,π)之间,需要采用相位解包裹算法进行真实相位的提取。常见的数值解包裹算法一般都存在计算量大、计算耗时的问题,且当待测非球面表面梯度较大时,数值解包裹算法可能会给测量结果引入误差,降低检测精度。
双波长全息法的原理[14]是采用两种不同波长光源进行非球面面形误差测量,得到两幅携带非球面面形误差的干涉图。通过合成算法求解出两种波长的等效合成波长,相当于用一个波长较长的光源进行非球面面形误差的检测。由于干涉仪产生的干涉图条纹间距在一定程度上会依赖于干涉仪光源的波长,干涉仪光源波长越长,干涉条纹越稀疏。因此,双波长全息法能够避免数值解包裹算法误差的引入,即使待测非球面表面梯度很大时,双波长相位解包裹得到的相位分布精度仍然高于传统数值解包裹算法。

图13 双波长数字全息三维成像装置示意图
图13为双波长数字全息三维成像装置示意图。波长为660 nm的激光光源入射到分光镜BS1,被分为两束,一束被反射镜M1反射到达分光镜BS2作为参考光束,另一束被反射镜M2反射后通过被测物体到达分光镜BS2作为测试光束。参考光束与测试光束在分光镜BS2处发生干涉并被记录成一幅数字全息图。波长为671 nm的激光传输路径与第一种波长激光传输路径一致,参考光束与测试光束发生干涉被记录成另一幅数字全息图。两幅图像相乘得到的合成图像包含的相位信息分布与等效合成波长通过检测系统生成的干涉图样相同。通过相位解算,便能求解出待测非球面的面形误差。
2.4 倾斜波干涉法
倾斜波干涉仪[15](In Clined Wave Interferometer,TWI)是在泰曼格林干涉仪的基础上改进而来的。与泰曼格林干涉仪的不同之处:首先,在光路中的傅立叶平面上放置光阑,以限制探测器处探测到的条纹密度。其次,装置中采用位于准直系统焦平面上的二维点光源阵列进行照明,可以使得测试光束到达被测面时携带不同倾斜波。如图14所示[16],二维点源阵列发出的光经过分光棱镜后被分成两束光,其中一束为参考光束,另一束为测试光束。在测试光路中,二维点源阵列发出的多束入射光,经过准直透镜组后产生多束具有不同倾角的球面波,因此可以认为二维点源阵列的使用在测试光路中引入了球面波点源阵列。多重倾斜球面波入射到待测样品上,对待测样品的局部区域进行梯度补偿,然后经待测样品反射回来的携带有待测样品面形偏差的倾斜波面再次经过准直镜组后入射到分光棱镜上,在分光棱镜处与参考波面发生干涉,经成像透镜后形成干涉图被CCD接收。通过对获得的干涉图进行解算、重构将待测样品的面形信息恢复出来。
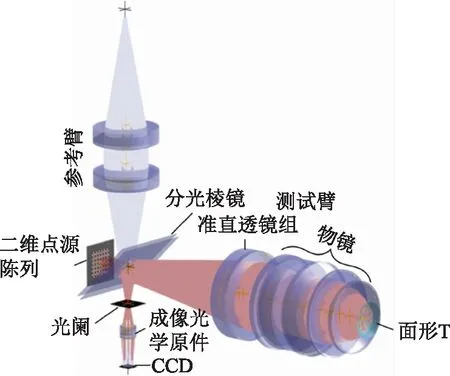
图14 倾斜波干涉仪原理装置图
在非球面非零位的干涉检测中,非球面上任意一点的实际法线与非球面最佳拟合球面上该点的法线之间存在偏转角,这就导致入射光经过待测非球面后无法原路返回。此时测试波面与参考波面发生干涉时可能会由于测试波前倾角过大,导致干涉条纹过密,CCD无法分辨。而倾斜波面干涉法是在检测系统中引入一个二维点光源阵列,产生多束具有不同倾角的入射波前,从而对被测非球面上各点的实际法线与最接近比较球面法线之间的偏转角进行补偿,以保证CCD可以探测到可分辨的干涉条纹。
2.5 部分补偿法
部分补偿法[17]是一种较新的非球面检测技术,与零补偿法不同,部分补偿法不要求补偿器完全补偿待测非球面的像差,允许补偿后检测系统像面处存在一定的剩余波前,只要控制该剩余波前像差在一定的范围内,使其引起的干涉条纹密度不超出探测器的分辨范围即可。
本节介绍一种应用部分补偿原理与数字莫尔移相技术[18]的非球面面形误差检测方案,检测原理如图15所示。利用改进的泰曼格林干涉仪,搭建实际测量系统,采集经部分补偿器补偿后CCD探测到的一幅实际干涉图。在光学设计软件中搭建虚拟干涉仪,其中待测样品为与待测非球面对应的理想非球面,代入部分补偿镜的结构参数,通过光线追迹得到虚拟系统理论干涉图。利用数字移相的方法,通过理论干涉图生成相位差依次为π/2的四幅移相虚拟干涉图。利用莫尔合成技术,将一幅实际干涉图分别与四幅虚拟干涉图相乘,得到四幅莫尔合成干涉图。通过对莫尔干涉图进行相位解算可以求解出非球面的面形误差信息。

图15 检测原理示意图
数字移相技术的引入能够省去传统机械移相装置的使用,精简系统机构,避免误差源的引入,提高干涉测量系统的稳定性。虚拟干涉仪的引入使得检测系统能够通过单帧实际干涉图完成非球面的检测,为非球面面形误差的瞬态检测提供了可能。而莫尔合成技术的引入,将虚拟干涉图与实际干涉图联系起来,实现了虚拟标准参考面与实际被测面之间的相干。利用虚拟干涉仪和数字莫尔干涉技术还能简化非球面测量系统的装调过程,采集一幅存在调整误差的实际干涉仪后,即可利用计算机优化算法得到失调量,并在虚拟干涉仪中完成模拟,直接得到精确地测量结果,免去了实际干涉仪繁琐的装调过程[18]。另外,部分补偿数字莫尔移相干涉法也使得非球面面形误差与面形参数同时测量成为可能[19]。
图16为用于凸非球面检测的部分补偿实例示意图[20]。光路中使用折反式部分补偿器。干涉仪出射的平行光经透射式透镜L1会聚后,穿过球面反射镜M1的中心开口入射到待测凸非球面M2上,经M2反射到达M1后原路返回到M2,光线第二次被M2反射后,沿入射时的传播路径原路返回,通过M1中心开口后经透镜L1后回到干涉仪中。
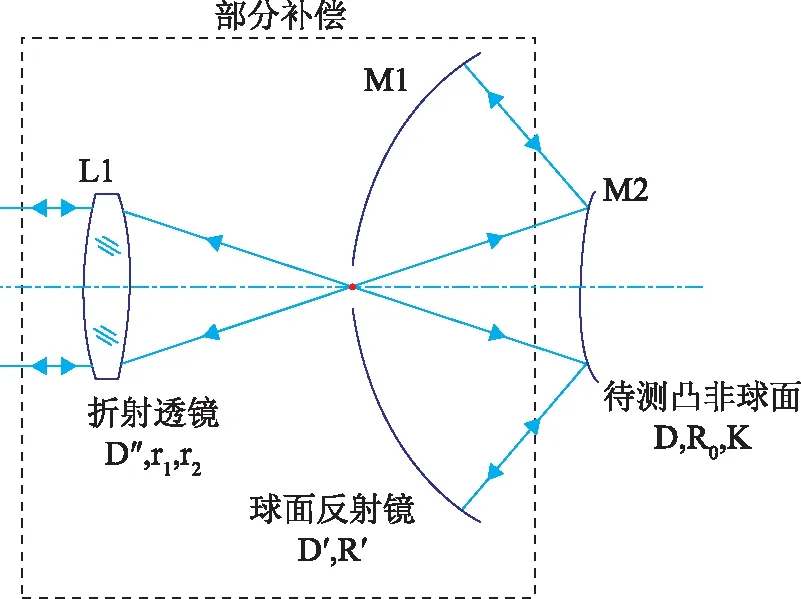
图16 折反式部分补偿器
该折反式部分补偿器有以下优点:首先,球面反射镜的使用易于实现光线的汇聚,相比较于完全使用折射式光学元件的补偿器,可降低折射式透镜折射率均匀性引入的误差,且易于加工,精度更高;其次,折反式光路结构避免了折射系透镜组补偿系统长焦距、大孔径的缺点,使得非球面的检测系统结构更加简单紧凑。
相对于零补偿法而言,由于检测系统允许一定量的剩余波前像差存在,部分补偿法法降低了补偿器设计和加工的难度,并且可以用一种部分补偿器对多种参数的非球面进行测量,用尽可能少的补偿器实现尽可能多的补偿,提高了测量的通用性[21]。
3 总结与展望
随着光学技术的不断发展,精密光学系统对非球面光学元件的需求日益增加,非球面高精度定量检测技术成为先进光学制造领域的前沿课题。本文调研了国内外非球面检测技术的研究现状和发展趋势,基于不同的测试原理,把现有的非球面检测方法归纳为零检验法与非零检验法,并对每种检验方法的特点进行了分析。
非球面的检测技术还需进一步的探索,以期实现基于单幅干涉图的非球面面形误差瞬态检测,以便在实际测量中,可以使用结构简单,测量效率高,且抗振效果好的检测装置。
