基于分布式压缩感知的异源图像融合方法∗

（中国电子科技集团公司第十研究所 成都 610036）

1 引言

在现代军事应用中，受天气、昼夜及隐身技术等影响，想要获取足够的目标信息，仅利用单源图像往往是不够的。较为先进的战斗机、轰炸机及无人机往往都同时携带了可见光、红外和SAR成像传感器，如何充分利用各种传感器图像的互补信息，将各种单源的图像进行充分有效的融合，形成一幅具有良好视觉效果、且目标突出的综合态势感知图像，是目前正在发生的且将继续进行的一项重要工作。

随着成像技术和传感器工艺的发展，所能采集到的图像越来越大，这对图像的存储和计算等操作的硬件设备带来了极大的挑战。压缩感知［1～2］是近几年发展起来的一种全新数据采样技术，具有在采样的同时进行压缩的优点，因而在信息论、信号处理、医疗成像等领域受到高度关注。基于压缩感知的成像技术，可以大大降低图像采集设备的成本，并能实现图像压缩数据的快速传输。

针对压缩感知成像的两幅异源图像进行融合，一种简单的方法就是先将各个源图像的压缩投影值通过压缩感知重建得到其近似的原始图像，然后利用金字塔分解［3］、小波变换［4］、高通滤波［5］等融合方法对两幅图像进行融合操作。但这种方法并不能有效解决计算量和存储量大的难题。

文中提出的基于分布式压缩感知的异源图像融合方法，在编码端通过分布式压缩感知投影，分别获得两幅单源图像的压缩投影值，在解码端，避开传统方法先解压再融合的思路，转而利用一种基于局部权值加权的融合规则，对两幅单源图像的压缩投影值进行融合，最后通过一次正交匹配追踪算法重建出融合图像。该方法进行压缩投影值的融合，保存的是融合图像的压缩投影值，而不是两幅源图像的像素灰度值，从而大大降低了数据存储量；该方法只进行一次压缩感知重建，且参与融合的是压缩投影值，从而大大降低了数据处理的计算量。

2 压缩感知理论

采用压缩感知理论的前提是信号具有稀疏性或可压缩性［6］，假设长度为N的信号 X在某组正交基或紧支撑框架Ψ上的变化系数是稀疏的，信号X可表示如下：

式（1）中a为稀疏系数，长度为N，a中只有K个系数为非零值。如果用一个与变换基Ψ不相关的测量基Φ∈RM×N(K＜M＜＜N)对信号 X进行测量，并得到测量数据Y∈RM，那么有

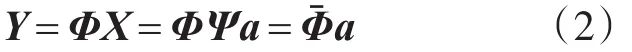
式（2）中Φˉ=ΦΨ∈RM×N，被称为传感矩阵，如果传感矩阵满足受限等距性［7］（Restricted Isometry Property，RIP）条件，那么就可以通过求解如下的最小l0范数问题来重建稀疏系数：

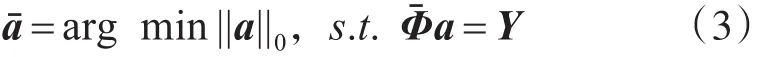
得到稀疏重建系数aˉ以后，就可以进一步由变换基Ψ 通过式（4）重构原始信号 Xˉ：

由于最优化问题，式（3）本质上是一个NP-hard问题，通常需要对该问题进行转换，如将l0范数转化为l1范数或l2范数加以解决，得到次最优解。常用的求解方法包括匹配追踪算法［8］、迭代收缩算法［9］、梯度投影算法［10］、凸优化算法［11］和非凸优化算法［12］等。

3 基于分布式压缩感知的异源图像融合方法

文中提出的基于分布式压缩感知的异源图像融合方法处理步骤如图1所示。

基于分布式压缩感知的异源图像融合方法，该方法主要包括分布式压缩感知投影、局部权值计算、投影值加权融合和压缩感知重建等步骤。

3.1 分布式压缩感知投影

压缩感知成像有效解决了传统成像方法计算量和存储量巨大的难题，同时具有在成像的同时进行压缩的优点，压缩感知投影是压缩感知成像的一个关键步骤。

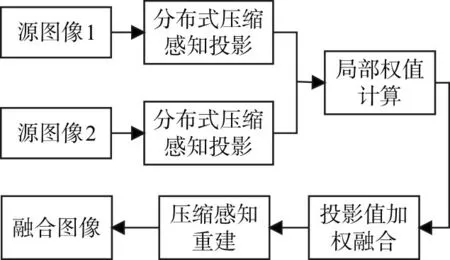
图1 基于分布式压缩感知的异源图像融合方法示意图

图像通常都具有较大的数据量，如直接将其展开成一维信号进行压缩感知投影，将使得压缩感知重建变得相当复杂，其计算量和存储量甚至会达到计算机难以承受的程度。故在压缩感知投影时，常以按列、按行或者分块等方式对其进行分布式压缩［13］。

在本文中，对图像数据进行分块的分布式压缩，在图像分块后，将每一块的值作为重新排列数据的一列，将源图像1和源图像2重新排列数据分别表示成 X1和 X2，大小均为N×N像素，那么压缩感知投影得到的压缩投影值Y1和Y2分别为

在式（5）和式（6）中，Y1∈RM×N；Y2∈RM×N；M N为压缩比；A∈RM×N为投影矩阵。考虑到图像融合需在同一映射空间下进行的特殊性，故对X1和X2进行同一投影矩阵A下的压缩感知投影。

压缩感知理论要求传感矩阵满足受限等距性条件，文献［14］证明了当投影矩阵是高斯随机矩阵时，传感矩阵能以较大概率满足受限等距性条件。所以本文的投影矩阵均采用高斯随机矩阵，矩阵的每一个元素独立地服从标准正态分布。

3.2 局部权值计算

在获得压缩投影值后，需要在压缩投影域对异源图像进行融合，即对两幅异源图像X1和X2的投影值Y1和Y2进行融合处理。

从式（3）可以看出，在进行压缩感知重建时，需要将投影值矩阵的每一列作为一个整体来选取最佳的匹配位置。而压缩感知图像融合常用的方法即系数取大法［15］，该方法明显忽略了投影值的每一列是一个整体的前提，故未能取得较好的融合结果。

将投影值的每一列作为一个整体，进行异源图像投影值的加权融合是可行的。在相同的投影矩阵A下，投影值大的地方则代表了原始图像中灰度值较大的区域，在可见光、红外和SAR图像中，这些区域往往包含了重要的目标信息。然而，同一个目标在不同的源图像中将表现出不同的特征，因此在归一化后，几乎不存在同一场景的所有目标在某种源图像中灰度值均高于另一种源图像的情况。故本文采取基于局部权值的投影值融合规则，即将两种源图像影值的每一列单独计算权值，然后求取加权和。

首先计算压缩投影值Y1和Y2每一列的数值和，即

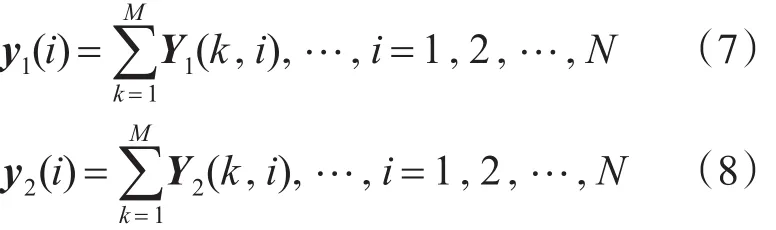
从而可以求得源图像1和源图像2压缩投影值每一列的权值分别为

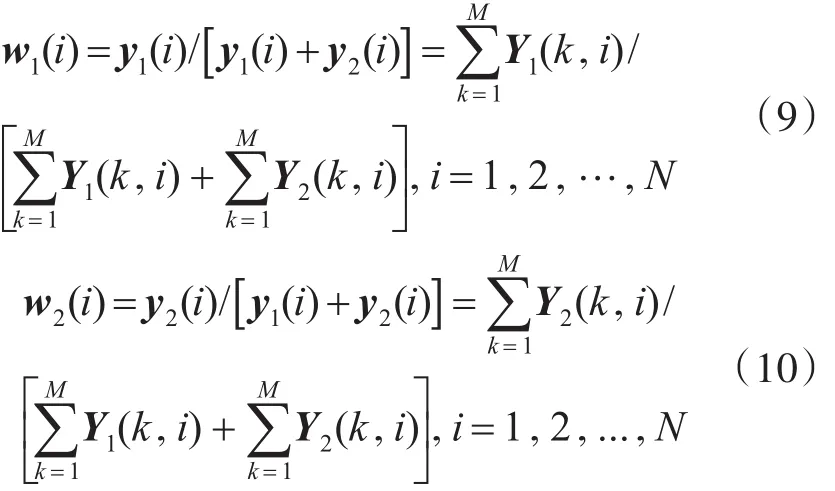
3.3 测量值加权融合

在求得源图像1和源图像2压缩投影值进行融合的局部权值之后，通过式（11）就可以计算出融合后的压缩投影值。

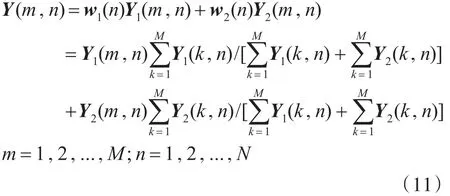
3.4 压缩感知重建

得到融合后的压缩投影值Y之后，通过式（12）便可以获得重建的稀疏系数a。

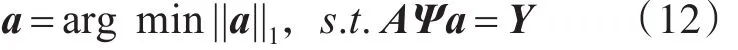
式（12）中，Ψ∈RN×N为稀疏矩阵。本文采用的求l1优化问题的方法为正交匹配追踪算法。

在得到稀疏系数后a，通过求解式（13）就可以得到融合图像。

4 仿真及结果分析

本文采用像素均为400×400的同一场景可见光和红外图像作为仿真对象，每一个像素以8灰度级量化，压缩感知的投影矩阵为高斯随机矩阵，图像压缩比为0.6，重建算法为正交匹配追踪算法，稀疏矩阵为离散小波变换矩阵。在Matlab7.8.0环境下进行仿真分析。

为了验证图像融合的效果，本文选用平均梯度g和平均交叉熵C作为衡量图像融合好坏的指标［16］，其具体公式如下：

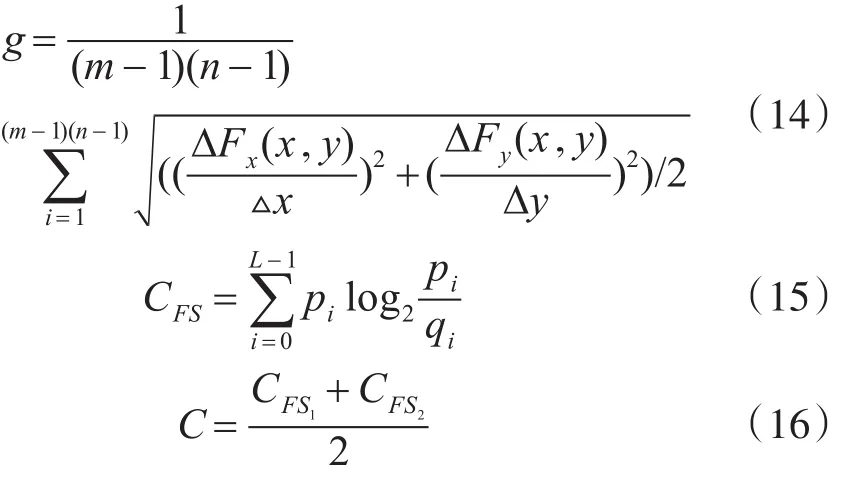
在式（14）中，F表示融合图像，其大小为m×n；在式（15）中，p={p0，p1，...，pL-1}和 q={q0，q1，...，qL-1}分别是原图像和融合图像的灰度分布；式（16）的C表示对两幅源图像与融合图像的交叉熵取均值，即平均交叉熵。

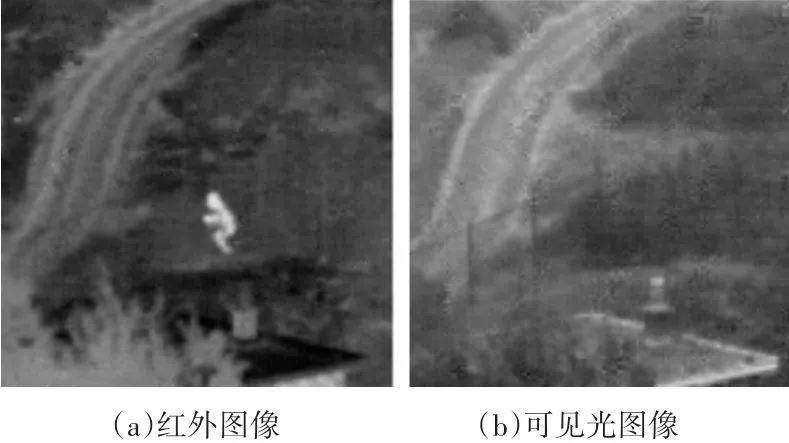
图2 同一场景的两幅源图像1

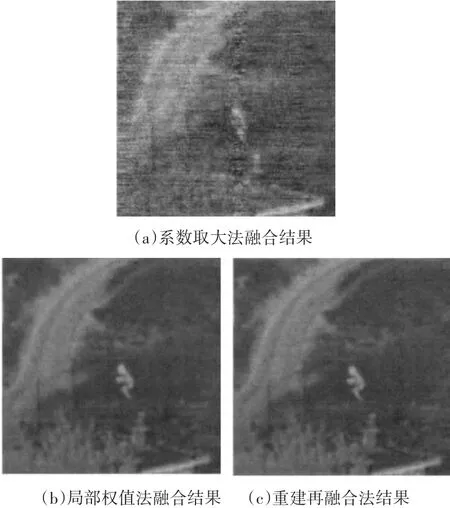
图3 不同方法融合结果对比1

本文以程序运行时间T和需要存储的图像数据量D来分别表示计算量和存储量。通过仿真，得到了基于分布式压缩感知的异源图像融合方法（局部权值法）、基于系数取大的压缩感知融合方法（系数取大法）与基于先重建再融合的压缩感知融合方法（重建再融合法）的对比结果图如图2～图5所示。

图4 同一场景的两幅源图像2

图5 不同方法融合结果对比2

通过对多组图像进行多次的Monte-Carlo实验，得到了三种方法四个指标的统计结果如表1所示。

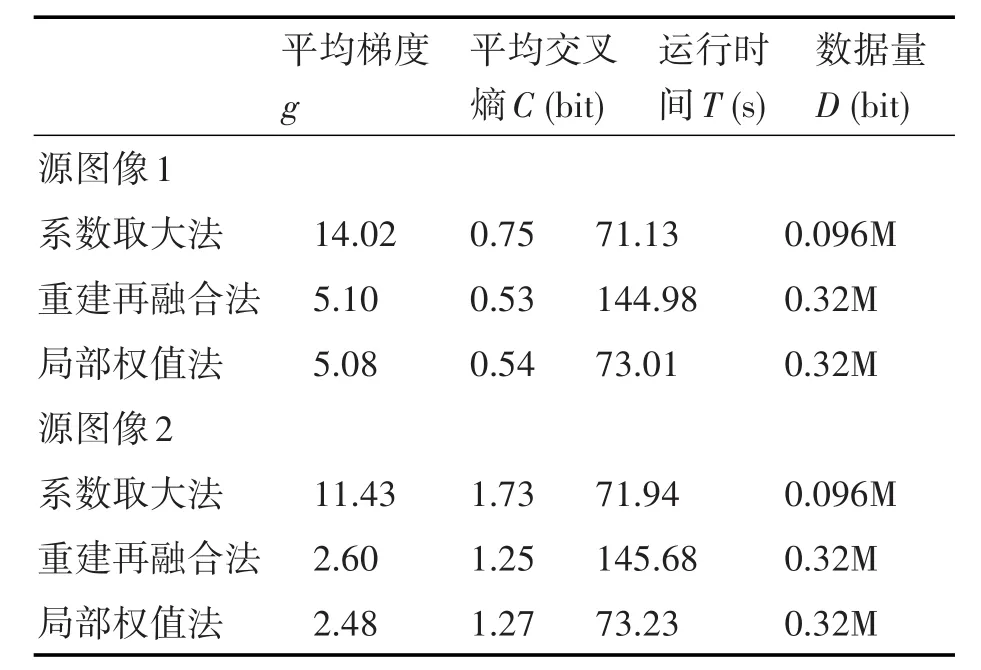
表1 融合结果对比指标

从图3和图5可以看出，在相同的实验条件下，系数取大法融合得到的图像轮廓模糊，细节不清楚，总体质量较差；而局部权值法和重建再融合法均能实现图像较高质量的融合，表现在轮廓清晰，细节明了，两幅图像在视觉上没有明显的差异。

从表1可以看出，重建再融合法与局部权值法在平均梯度和平均交叉熵两项指标上相当，无明显差异，而系数取大法这两项指标则明显偏高。平均梯度反映的是图像的灰度变化情况，较大的平均梯度既表示融合图像包含较多的细节信息，也可以理解为图像较为模糊，没有明显表征目标信息的平滑区域，很明显，在这里属于后者；平均交叉熵反映的是融合图像和源图像之间的差异，其值越小，则融合图像从源图像提取的信息就越多，融合效果越好。故从平均梯度和平均交叉熵两项指标来看，重建再融合法与局部权值法明显优于系数最大法。

从表1的运行时间和数据量两项指标来看，重建再融合法在计算量和存储量上都明显大于局部权值法。故本文提出的基于分布式压缩感知的异源图像融合方法，不仅能实现同一场景异类源图像的高质量融合，并能有效解决传统方法所带来的计算量和存储量大的难题。

5 结语

为了解决同一场景的异源图像在压缩传输及融合过程中由大数据量信息造成的计算量和存储量巨大的问题，本文提出了一种基于分布式压缩感知的异源图像融合方法，通过仿真表明该方法能有效解决系数取大法所造成的融合图像模糊缺陷，并相较于重建再融合法大大降低了计算量和存储量。基于分布式压缩感知的异源图像融合方法，有效解决了现代军事应用中同一场景不同成像传感器图像压缩、存储和融合的难题，具有较高的实用价值。