基于机器学习的中职学校流生预测研究
2019-01-02齐权
齐 权
(福建经济学校 计算机教研室,福建 福州350007)
一、引言
近年来,国家高度重视发展职业教育,支持各级各类职业教育办出水平、办出特色,各级职业学校的发展规模日益壮大。然而在规模扩大的背后,职业学校的学生流失现象十分严重,与大规模的招生数量形成了较大的反差。据福建省教育统计年鉴统计,2013-2015届中等职业学校学生的流失率分别为26.2%、39.6%和42.6%,中职学校学生的流失率不仅高且有逐年上升的趋势,甚至还有部分中职学校专业的流生率超过了50%,试问中职学校如此高的流生率背后,又能培养出多少符合社会经济发展的毕业生呢?然而,导致一个学生流失的因素或许有许多,但一定与学校管理是密不可分的。本文中提到的学生流失统称为流生。
二、传统的流生研究
职业学校学生流失的因素是多方面的,但归纳起来分为内因和外因。内因主要是指由学生自身的原因所引起的流生,而外因是指受家庭、学校和社会等因素的影响而导致的流生。其中,内因对流生起着最直接的、决定性的作用,然而内因的形成也是外因作用的结果。因此,外因对学生流生的影响起着至关重要的作用。目前,多数中职学校对流生的研究主要是以人脑学习的模式为主,即相关管理人员以学习到的先进理论结合自己的实践经验来分析流生产生的因素,最后给出相应的整改措施来加强学校的管理工作,以达到减少流生的目的。
基于专家经验的人脑学习模式的流程如图1所示。

图1 人脑学习模式流程
人脑学习的模式对于解决流生问题确实取得了一定的成效,但随着职业教育信息化建设的不断推进,在日常的教育教学工作中积累的数据量越来越大,数据种类也越来越多,面对如此繁杂而又庞大的教育教学数据,这种传统研究模式的局限性逐渐显现,一方面很大程度上受限于专家本身的知识与经验水平,另一方面也无法从海量的数据中分析出与流生相关的数据以及数据间的关联,而且与流生相关的因素越多,越容易干扰管理者的决策。因此,这种模式对于解决中职学校流生问题也是十分有限的,无法精准分析每所学校产生流生以及每个流失学生之所以产生的关键因素,也就无法帮助管理者做出正确的决策,学校也无法建立一套科学合理的精细化管理体系。
三、基于机器学习的流生预测研究
针对当前职业教育中传统人脑学习模式的不足,本文提出一种基于机器学习的新模式来代替人脑学习的模式,这种机器学习新模式的使用也是一个数据挖掘的过程。数据挖掘是集数据库、统计学、人工智能等技术形成的一个新兴领域,它不仅可以处理海量的复杂数据,还能够处理不确定数据和不完整的数据,能够在海量的数据中发现有价值的数据。
基于机器学习的流程如图2所示。
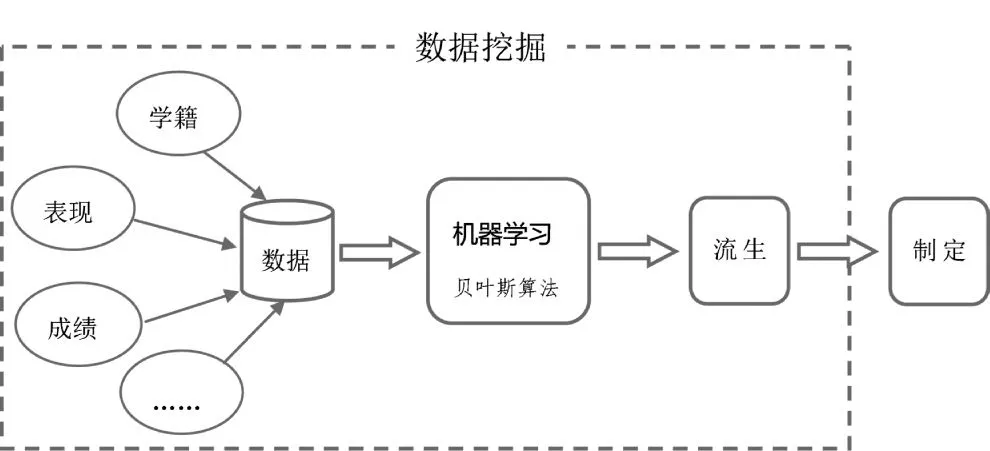
图2 机器学习模式流程
新模式的核心主要是通过数据挖掘算法来训练出数据模型,针对本文研究内容的特点,主要采用的是贝叶斯算法来训练流生数据模型。贝叶斯算法是数据挖掘技术的经典算法之一,它是一种利用概率统计知识对样本数据进行分类和预测的算法,在某些特定的条件下,朴素贝叶斯分类算法的准确率已经超过了决策树和神经网络等分类算法,并且该算法能够运用到大型数据库中,具有易实现、精度高和速度快的特点。新研究模式的主要研究过程如下:
1.流生分析
职业学校学生流失的因素是多方面的,但归纳起来分为内因和外因。内因主要是指由学生自身的原因所引起的流生,而外因包含的是家庭、学校和社会等因素的影响而导致的流生。其中,内因是对流生起着最直接的、决定性的作用,然而内因的形成也是外因作用的结果,因此,外因对学生流生的影响起着至关重要的作用。对于中职学校流生原因的分析可以从个人、家庭、学校、社会等四个方面展开。
2.数据理解
通过以上流生原因分析,基本确定了影响学生流失各个环节的因素,因此,可以根据学校实际情况结合流生分析的四个方面来收集、整理数据。例如,学生学籍信息数据、学生在校(含初中)成绩数据、学生在校表现(含初中)数据、学生的社交能力数据、学校的专业建设数据等。
3.数据处理
采集的原始流生数据一般是有噪声的、不完整的和不一致的,需要通过预处理技术对数据进行清理、集成和离散。数据清理主要是去除掉一些可能影响流生预测的噪点数据,补充缺失部分的数据,让数据格式符合机器学习的规范;数据集成主要是将数据采集过程中的片断数据整理成一个流生数据集;数据离散化则是将集成后的数据值域差别比较大的属性,离散化为差别较小的属性,更有利于数据挖掘的效率和挖掘模式的理解,从而提高数据自身的质量,提高数据挖掘过程中的效率和准确率。
4.建立流生数据模型
处理后的数据属性少则几十个,多则上百个,然而,对于数据模型的构建并不是样本数据属性越多越好,如此多的属性可能很多是冗余的数据属性,也可能许多数据属性与结果的关联度很弱,这些都会影响数据模型的质量,从而影响流生预测结果的准确率。因此,在流生数据模型构建过程中,首先需要进行样本属性选择,通过基于关联规则的特征选择(Correlation-based Feature Selection,CFS),评估出一个最佳属性子集,以降低样本属性的冗余度和关联度;然后,采用朴素贝叶斯算法进行分类预测,这种分类器在实际应用过程中十分简单且有效,又因为它的分类算法思想很朴素,所以又叫朴素贝叶斯分类法。这种分类法虽然十分简单有效,但是需要基于属性之间相互条件独立的假设,因此,针对算法的不足之处,本文主要采用一种加权后的朴素贝叶斯算法——k-最近邻局部加权朴素贝叶斯算法 (k-LW+NBC)来建立流生数据模型。
5.评估流生数据模型
由于流生数据模型采用的本身是一种简单高效的算法,因此,对于数据模型的评估,主要以分类模型的精准度为主。评估模型的精准度主要分成两个阶段:第一阶段,将样本数据采用随机算法分成两份,选取其中一份数据作为训练数据,将训练数据分别采用朴素贝叶斯算法(NBC)、决策树算法(ID3)、k-最近邻局部加权朴素贝叶斯算法(k-LW+NBC)训练出三种算法的流生数据模型;第二阶段,选取另一份数据作为评估数据,分别带入训练出来的三种流生数据模型进行N叉校验,将三者校验的结果进行对比,以验证流生模型的精准度。
6.应用流生数据模型
本文应用的数据来自于福建省内一所招生规模较大、办学条件较好并且具有一定代表性的中等职业学校近三年的数据。通过前期的数据采集、数据清理、数据构建、数据集成和数据的离散化处理,我们最终选择了11个属性、1414条数据作为本次流生研究的实验数据,作为该校的流生样本数据,部分数据样本如表1所示。
在整个模型建立的过程中,本文主要使用Weka工具进行了实验,通过实验数据表明,这种基于属性评估的局部加权朴素贝叶斯算法(CFS+k-LW+NBC),能够很好地处理噪声数据、降低数据维度、提高分类效率和精准度,在对职业学校学生流失预测的应用中,体现出了较好的效果,以某一职业学校的实验数据为例,该算法对于学籍状态为“退学”的学生预测准度最高达93.7%,足以说明该分类器的准度。最后,将评估数据集分别应用于朴素NBC算法和ID3算法进行交叉校验,三种算法的精准度如表2所示。

表1 某校部分流生样本数据
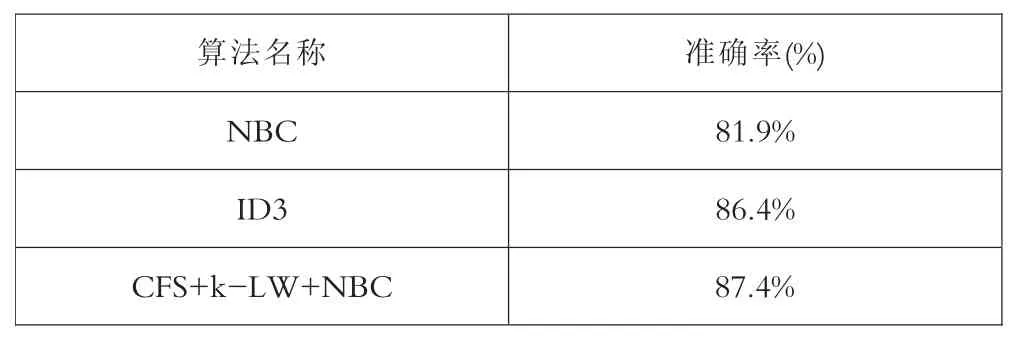
表2 三种算法的准确率对照表
通过前面的模型评估结果可知,基于属性评估的局部加权朴素贝叶斯算法(CFS+k-LW+NBC)是三种算法中精准度最高的,因此,我们可以运用该算法训练所得到的模型来对某职业学校的在校生进行流生的预测。
截至2017年8月,某职业学校拥有在校生人数5362人,通过数据清理后,得到有效的数据为5112条。现将5112条数据带入到训练的模型中,获得的预测结果如表3所示。
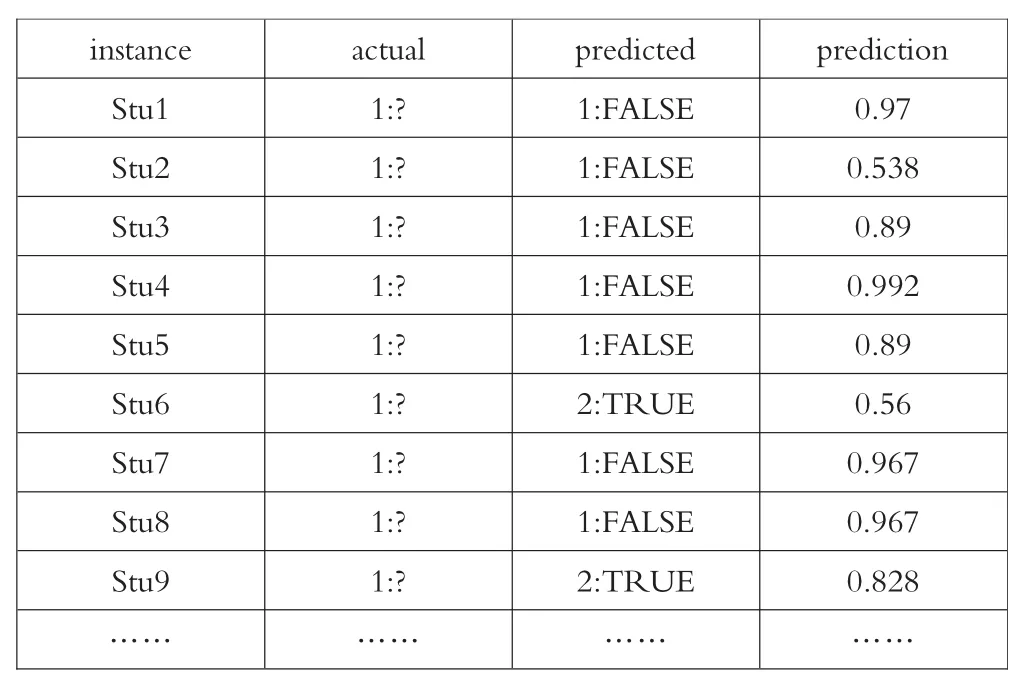
表3 某校流生预测部分数据表
通过该校的流生情况预测表可知,该校学生流生倾向可信度达70%以上的人数为1794人,占到总人数的35.1%,可信度达80%以上的人数为1513人,占总人数的30%。结合条件属性的分析可知,学生的不及格科目数量、违纪次数、选择专业的情况和是否为学生干部为类别属性的强关联属性。
四、结论
在即将到来的大数据时代,职业学校传统的基于专家经验的人脑学习模式已无法适应当前信息化、精细化管理的要求,因此,针对人脑学习模式的弊端,本文提出了一种基于机器学习的流生预测研究的新模式,以适应当前数字化的发展需求,实现职业学校精细化管理的目标。通过本文应用案例中建立的流生数据模型可知,学生的不及格科目数量、违纪次数、选择专业的情况和是否为学生干部对中职学生流失的影响非常大,这些关键因子同时也折射出该校在教学管理、学生管理、专业建设以及校园文化中的不足,在后期的管理决策中应该重点考虑。例如,通过加强学生德育工作和学生管理工作以减少学生违纪现象;通过创新教学方法和评价模式来提高课堂教学质量和学生成绩,以减少学生的不及格科目;开展形式多样的社团活动,以此来带动校园文化的建设;加大校企合作力度,重新调研专业方向和制定课程体系结构来增强专业活力等等。而对于在校生的流生预测,则可以结合学校的信息化系统建设,监测相应流生模型中的关键因素,对在校学生进行实时的预测,同时结合学校自身的实际情况,设置一个可信度的值作为阈值,对可能流失的学生进行预警,将预警的学生以及影响学生流失的因素报送给相关管理部门,帮助管理者有针对性地制定策略,以减少在校学生的流失率。
