基于Geostudio与Flac 3D的浅层滑坡稳定性研究
2019-01-02张骞棋
张骞棋
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
目前边坡稳定性研究广泛采用刚体极限平衡法,GeoStudio数值分析软件中的SLOPE/W 模块是以极限平衡理论为基础来分析边坡稳定性的, 其分析过程采用瑞典条分法、Janbu法、Bishop法、Morgenstern-Price法 (M-P法) 等原理, 能够根据地质条件建立边坡模型,较为准确得出边坡稳定或失稳时的安全系数,并搜索出可能的破坏面[1]。但是传统的刚体极限平衡理论没有考虑岩土体内部的应力应变关系,无法分析边坡破坏的发生和发展过程。
与传统的极限平衡法相比,各种数值模拟分析方法在分析大变形上面具有很大优势。美国Itasca Consulting Group, Inc公司开发的Flac 3D是一种基于拉格朗日差分法的有限差分程序,具有丰富的本构模型,其前后处理功能强大,可以模拟模型趋于平衡的整个过程,通过对过程中的应力场、位移场及塑性变形特征的分析,验证边坡变形及裂缝,预测其变形趋势[2-3]。但是Flac 3D数值分析方法无法像极限平衡法一样直接给出稳定系数,而软件自带的强度折减程序模块计算安全系数的方法适用于网格规则、规模较小的边坡,针对大型边坡及网格数量较多的模型则运算效率极低,甚至报错,只能通过基于应力场和位移场的关联流动法、强度折减法等方法进行计算,而这则大幅增加了计算时步,在建模时微小的差异都有可能带来计算结果的较大误差,无形中增加了计算代价[2]。
本文以某公路堆积体边坡为例,旨在通过基于极限平衡理论的Geostudio软件的SLOPE/W 模块计算堆积体边坡在天然工况下的稳定系数,搜索潜在滑面,同时,利用Flac 3D模拟边坡变形的整个过程,根据应力场、位移场特征,与Geostudio计算结果对比,分析其发生应力集中与最大变形的部位,为边坡稳定性分析提供一种更为简洁、可靠的方法,为边坡治理提供更为可靠的技术支持。
1 工程概况
研究区滑坡位于某河段上游左岸,深切河谷地貌,雨季较长,地表水量较大,区内未见地下水发育。滑坡平面形态呈圈椅状,纵向长约42 m,横向宽约55 m,整体坡度约50(°),中上部位较陡可达64(°),滑坡方量约0.5×104m3。该滑坡变形以侧缘纵向拉裂缝、中上部横向拉裂缝为主,主拉方向与滑动方向大体一致。滑坡目前处于蠕滑状态。
滑坡区基岩岩性为二叠系栖霞组厚层块状灰岩,含燧石结核,滑体物质组成主要为碎、块石黏土,母岩成分以灰岩为主,碎石含量较高,粘土呈硬塑状态。
2 数值模拟计算
2.1 力学模型与力学参数
本文滑坡为松散堆积体滑坡,因此两种数值分析方法均采用Mohr-Coulumb本构模型进行模拟计算[4]。结合室内试验、滑体物质成分、滑坡结构特征类比同类工程经验及参数反演,最终确定滑带土物理力学参数如表1。

表1 物理力学参数
根据以上力学参数,分别建立了Geostudio与Flac 3D二维模型,区内不发育地下水,不考虑地下水位以及地震力的影响,如图1、图2所示。

图1 边坡Geostudio二维模型
图2 边坡Flac 3D模型
模型断面宽度为40 m,高度为36 m,Flac模型为通过ANSYS-FLAC接口划分网格后导入flac中,共216个单元,408个节点。
2.2 数值模拟计算及结果
本文通过Geostudio计算获得滑坡稳定系数,经过模拟计算,得到在天然工况下几种计算方法的稳定系数,见表2。
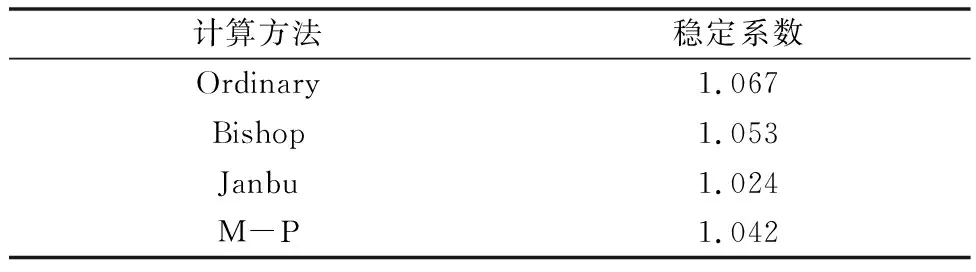
表2 不同计算方法的稳定性系数
由表2可知,在天然工况下,该堆积体边坡均处于欠稳定状态。其中,摩根斯坦法作为极限平衡法的一种,由于考虑因素较多,除了计算稳定系数外,还可以分析各土条的受力情况,因而是比较精确的[1]。因此,后续的对比分析中采用M-P法计算得到的数据。
Flac 3D模拟计算过程中,最大不平衡力趋于0,表明体系最终达到了力平衡状态,如图3所示。
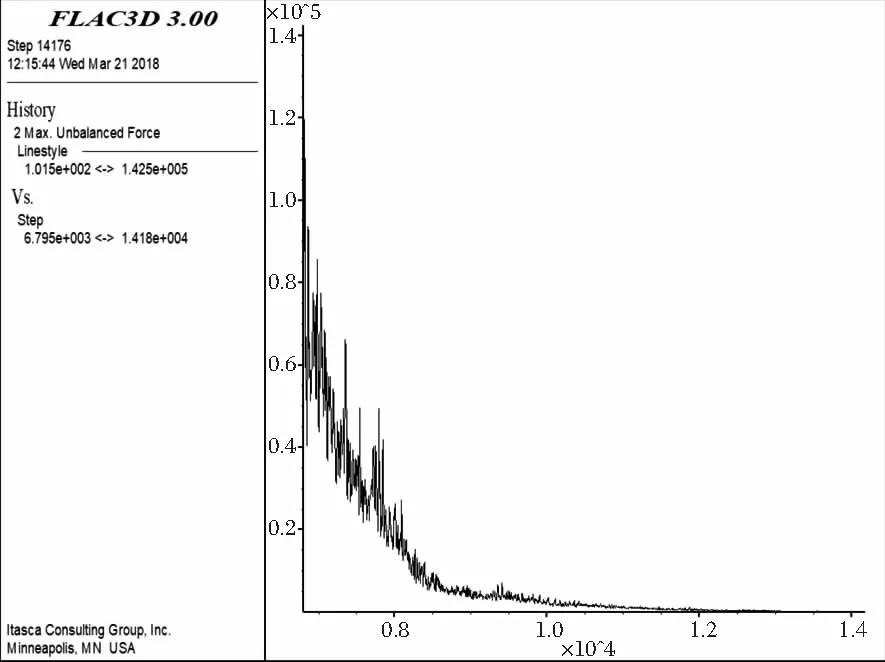
图3 Flac 3D不平衡力演化全程曲线
3 模拟成果分析
3.1 滑体潜在滑面
Geostudio计算后,可以清楚得到滑坡潜在滑面及滑带,如图4所示。
Flac 3D计算后得到的位移云图如图5所示。
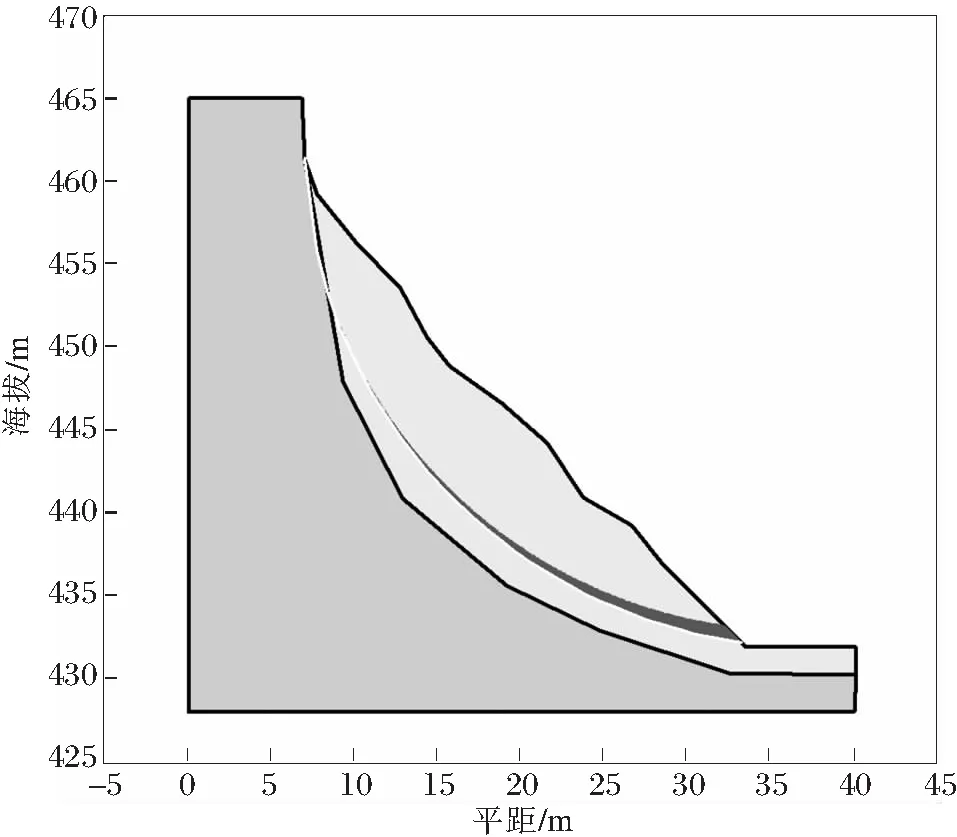
图4 Geostudio计算滑带

图5 Flac 3D计算位移矢量图
由图5可知,滑体在上部位移表现为“沉降”,中部位移与坡面近乎平行,下部位移在坡脚表现为“剪出”。与此同时,Geostudio显示的潜在滑面与Flac 3D模拟的位移形态近似一致,表明边坡的潜在破坏以浅层圆弧形剪切破坏为主。
3.2 位移场计算结果分析
通过Flac 3D模拟计算,可以得到滑体在X方向与Z方向的位移云图,如图6、图7所示。
由图6、图7可知,滑体于前缘坡脚位置发生X方向最大位移,后缘坡顶位置发生Z方向最大位移。这与Geostudio模拟搜索得到的滑带位置基本一致。
3.3 应力场规律分析
根据Flac 3D数值计算得到各应力云图如图8所示。

图6 滑体应力平衡时X方向位移云图

图7 滑体应力平衡时Z方向位移云图

图8 最大主应力云图
由图8可看出最大主应力与坡面基本平行,并延伸到坡脚,这对边坡稳定十分不利。同时,在基覆界面及坡脚位置产生应力集中效应,说明此处为变形破坏发生的位置。
通过Geostudio软件计算得到剪应力与最大主应力曲线如图9、图10所示。
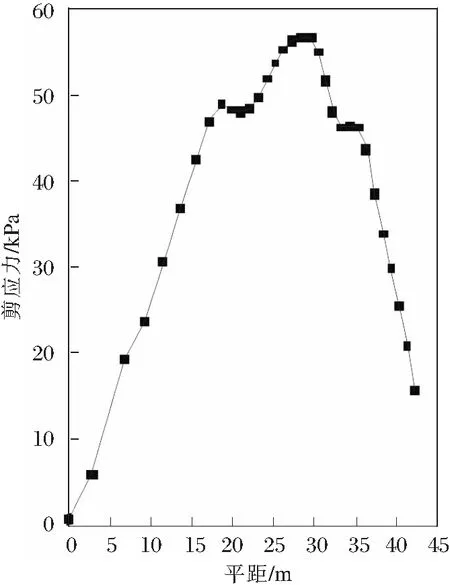
图9 剪应力变化曲线
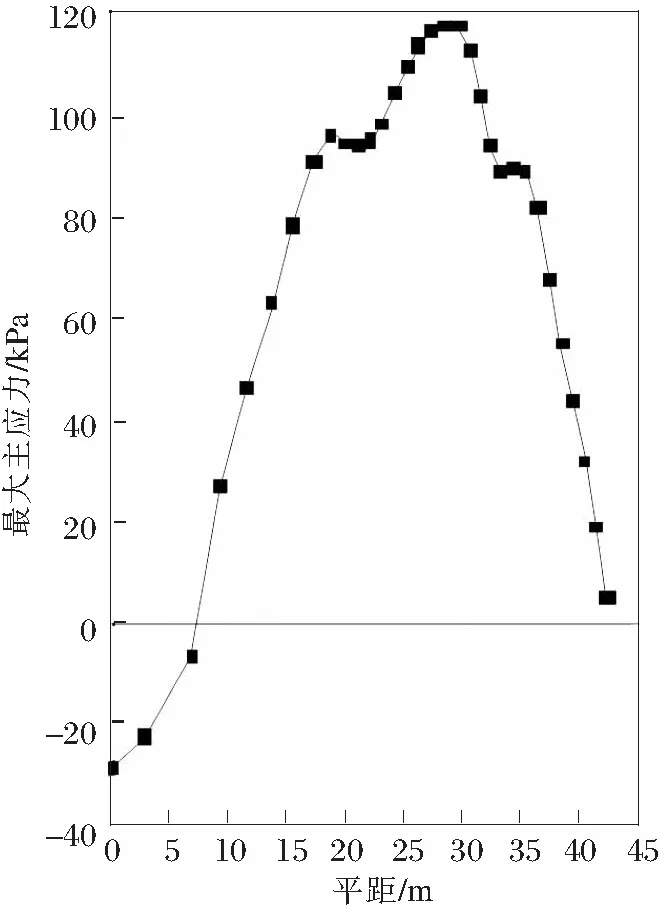
图10 最大主应力变化曲线
由图9、图10可知,在坡脚位置X=30 m处发生最大剪应力与最大主应力,与Flac 3D模拟计算得到的结果相一致。
3.4 最不利变形位置
Flac 3D模拟计算得到的剪切增量云图见图11,块体塑性区分布见图12。
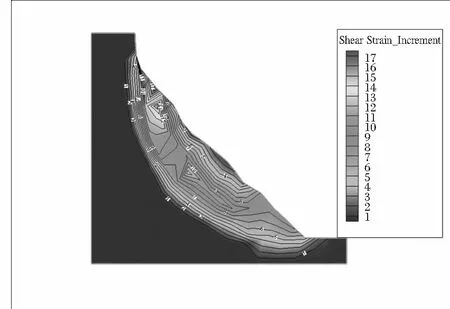
图11 剪切增量云图
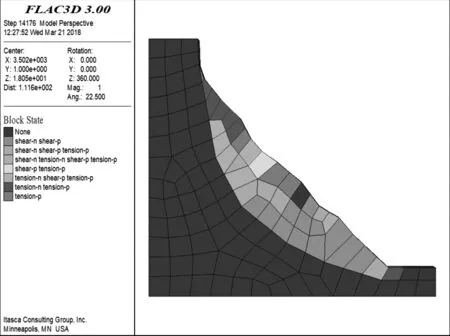
图12 块体塑性区分布图
由图11、图12可知,滑坡体在滑坡前缘与后缘上部产生横向裂缝的部位发生应力集中,产生变形最大。
3.5 滑坡机制分析
结合Flac 3D计算得到的应力分布特征与位移分布特征和Geostudio计算得到的剪应力与最大主应力曲线图,分析滑坡形成机制:滑坡体坡面较陡,雨水沿后壁进入滑坡体内,在基覆界面形成软弱带,滑体内部发生蠕变,在滑坡前缘与后缘上部产生横向裂缝的部位发生应力集中,坡顶产生竖向位移,推挤下部块体移动,最终在坡脚剪出,形成圆弧滑面的推移式滑坡。
4 处理措施建议
根据Geostudio计算结果,得出在天然工况下滑坡处于欠稳定状态,并搜索得到潜在滑面,结合Flac 3D数值模拟计算结果,验证了Geostudio计算结果正确,并由Flac 3D位移、应力与剪切塑性区云图得知,滑坡在坡脚及坡顶横向裂缝部位发生应力集中,产生最大变形。因此,在滑坡治理设计中,应当考虑坡脚抗滑与坡顶锚固相结合的设计思路。
滑坡堆积体常规治理方案主要包括抗滑桩、预应力锚索、减重和反压、挡土墙、锚索桩等[5]。结合本边坡工程特点,推荐采用挡土墙+预应力锚索框架梁的设计方案进行治理。在坡脚位置设计重力式挡土墙,后缘坡顶横向裂缝处设计一排预应力锚索框架梁。另外,降雨对滑坡稳定性具有十分重要的影响,因此,在挡土墙顶部与滑坡后缘设置截水天沟与排水沟,做好防排水设计。
5 结 论
通过采用基于极限平衡原理的Geostudio与基于有限差分原理的Flac 3D两种数值模拟软件,对某堆积体滑坡稳定性进行研究。得出以下结论:
1)Geostudio计算得到的滑坡稳定系数与Flac 3D模拟滑坡趋于平衡状态一致,均为欠稳定状态。
2)Geostudio搜索得到潜在滑面与Flac 3D模拟得到的剪切应变和塑性变形区一致。
3)结合Flac 3D计算得到的应力分布特征与位移分布特征和Geostudio计算得到的剪应力与最大主应力曲线图,分析滑坡形成机制:滑坡体在滑坡前缘与后缘上部产生横向裂缝的部位发生应力集中,坡顶产生竖向位移,推挤下部块体移动,最终在坡脚剪出,形成圆弧滑面的推移式滑坡。
4)根据分析结果,结合工程特性,提出挡土墙+预应力锚索框架梁+排水的处理方案。
5)结合Geostudio与Flac 3D两种基于不同计算原理的边坡稳定性分析方法,可以克服Geostudio无法分析应力应变过程、预测变形趋势与Flac 3D无法直接得出稳定性系数的缺点,分析过程更为简便。
