基于用户兴趣相似度与熟悉度的兴趣点推荐算法*

王 峥 张 成

（1.南京烽火星空通信发展有限公司 南京 210019）（2.武汉邮电科学研究院 武汉 430074）（3.南京烽火天地通信科技有限公司 南京 211161）

1 引言

近几年，随着智能手机的普及，基于位置的社交网络LBSN（Location-Based Social Network）发展十分迅速，国外的Foursquare、Gowalla，国内的微信、微博等社交网络平台，注册用户量已超千万，微信注册用户量更是多达9.27亿。LBSN使用户可以用一种签到的方式发布与当前位置相关的信息（如评论、照片），与其他用户分享自己的观点。通过分析LBSN的用户签到数据，可以得到用户的兴趣倾向，从而衍生出一系列的社交网络推荐服务，比较典型的应用有好友推荐、兴趣点推荐和活动推荐，本文主要针对兴趣点推荐进行算法研究。目前常用的兴趣点推荐算法可分为三类，分别是基于协同过滤的推荐算法［1］、基于矩阵特征化的方法［2］以及基于随机游走的方法［3］。其中应用最广泛的是协同过滤算法，协同过滤推荐算法主要有基于用户的User-CF算法［4］和基于项目的Item-CF算法［5］，这些方法在兴趣点推荐中主要根据用户已有的签到行为数据来预测和推荐，但这些算法在引入社交网络关系数据时运用不够充分。本文提出一种基于用户兴趣相似度和熟悉度的兴趣点推荐算法，向用户推荐一组用户感兴趣的地点（即兴趣点POI）。该方法主要特点如下：

1）该方法在一定程度上克服了用户签到矩阵的稀疏性对用户相似度计算的影响。采用非负矩阵分解将用户签到矩阵分解成用户特征矩阵和地点特征矩阵，利用用户特征矩阵来计算用户之间的兴趣相似性，使得最后的推荐结果更加精确。

2）引入六度分隔理论［6］和三度影响力规则［7］，完善用户之间熟悉度的计算，提高推荐结果的精确度。

2 相关工作

最初，Ye等［8］将兴趣点推荐引入到LBSN中，他们认为朋友关系会对用户的地点选择有很大的影响，因此，提出了一种基于好友社交关系的协同过滤方法；随后，Ye等［9］又分析了地理位置对用户地点访问行为的影响，他们假设用户更喜欢访问距离近的地点，从而建立幂分布模型来模拟地理距离与访问可能性大小的关系；除了幂分布外，Cho等［10］和Cheng等［11］通过多中心髙斯分布来模拟地理位置的影响。Zhang［12］等利用核密度估计模型，将每个用户的地理影响力建模为个性化的距离分布。

Shi Yue等［13］根据用户历史位置数据建立一个类别-正则矩阵，再基于这个矩阵进行兴趣点推荐；孙光福等［14］提出一种基于时序消费行为的最近邻建模方法，通过用户（产品）的相互影响关系，产生更为精准的推荐结果。还有一些学者在传统的推荐方法基础上进行改进并应用于兴趣点推荐中，如Berjani等［15］采用正则化奇异值分解（Singular Value Decomposition，SVD）模型对地点进行评分预测；Leung等［16］将用户、地点进行划分聚类，得到相似用户类在相似地点类上的新的签到矩阵，然后通过传统的协同过滤方法进行兴趣点推荐。

以上的研究取得了一定的成果，但是还存在着不足之处。传统的协同过滤算法关键是用户相似性的计算，但用户签到矩阵往往是高稀疏性，导致推荐结果不理想：在引入社交网络关系时上述方法都只考虑到用户间距离为二的熟悉度，这与现实生活情况不符。根据六度分隔理论［6］，一个人与任何一个陌生人的距离不会超过六个人（距离为六），在此基础上，Nicholasa A Christakis研究发现，相距三度之内是强连接，强连接可以引发行为［7］，即两个用户之间不存在共同好友时，但两个用户间的距离为三时，仍然存在着一定的熟悉度。本文提出一种基于用户兴趣相似度和熟悉度的兴趣点推荐算法，采用非负矩阵分解的方法计算用户兴趣相似度，根据三度影响力规则将用户间距为三的熟悉度融入用户熟悉度计算中，以改善用户间的信任质量，提高兴趣点推荐精度。

3 兴趣点推荐算法

用户在接受他人推荐的一个陌生地点时，两人之间的熟悉度和兴趣相似性是最主要的考虑因数。本文通过分析用户的好友关系数据来评估用户之间的熟悉度，并根据用户的签到数据来评估用户之间的兴趣相似度，结合熟悉度和兴趣相似度得到信任度，最终根据Top-N推荐得到推荐列表。推荐模型如图1所示。

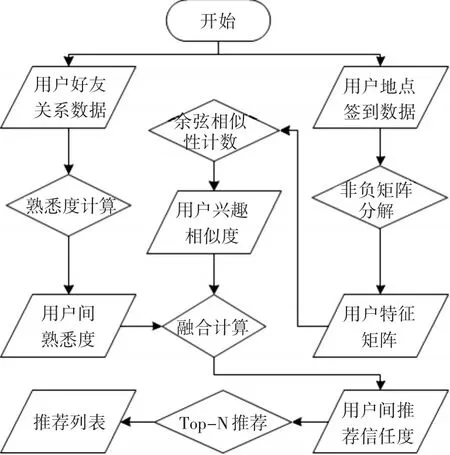
图1 基于用户兴趣相似度和熟悉度的兴趣点推荐模型

3.1 用户熟悉度计算

为用户进行兴趣点推荐时，用户之间的熟悉度是一个很重要的参考因素，且两人之间的熟悉度越高，推荐的地点越有可能被采纳。在基于社会关系的推荐算法中，“朋友的朋友也有可能是我的朋友”是一条大众普遍接受的假设。本文用户之间的熟悉度也基于共同好友数来确定。但熟悉度不能单纯地通过统计两用户间的共同好友数得到，因为熟悉度本身是非对称的。如某用户的交际范围越广，或在LBSN中越活跃，该用户越有可能与其他用户拥有很多共同好友。但一个人的精力是有限的，仅从熟悉度角度看，他们之间的熟悉度属性并不高。综上所述，本文采用的熟悉度计算公式如下：

式（1）中，Fam（u，v）表示用户u和用户v的熟悉度，|Fu∩Fv|表示用户u和v之间的共同好友数，| Fu|表示用户u的好友数。该公式表明，用户u和v之间的熟悉度与他们之间的共同好友数成正比，与用户u的好友数成反比。即活跃度越高的用户，在共同好友数相同的情况下，与其他用户的熟悉度越低。

以上情况是两用户间存在共同好友时熟悉度的计算方法，但两用户间不存在共同好友时，根据文献［15］提出的三度影响力规则，即两用户不存在共同好友时，但两用户之间的距离为三时，仍然存在着一定的熟悉度。本文两用户间不存在共同好友（距离为三）时熟悉度计算公式如下：

式（2）中，Fam（u，v）表示用户u和用户v之间的熟悉度，a为不为用户u和用户v的任一其他用户。

3.2 用户兴趣相似度计算

经典协同过滤算法的关键问题是相似性的计算，其中用户相似性准确来说是用户兴趣相似性。在度量兴趣相似性时会用到用户对项目的评分矩阵，常用的方法有余弦相似性、相关相似性等计算方法。本文采用余弦相似性，其计算公式为

式（3）中，sim（u，v）表示用户u和用户v的相似性，和v→分别表示用户u和用户v的评分向量，n为评分矩阵中的项目数，Rui和Rvi分别表示用户u和用户v对项目i的评分。

但因为用户评分矩阵的稀疏性，直接利用余弦相似性计算用户间的兴趣相似性效果不佳。本文采用非负矩阵分解（NMF）的方法，将用户地点签到矩阵 Rm×n分解成两个非负矩阵Wm×k和 Hk×n的乘积，其中k为特征数，Wm×k为用户特征矩阵，Hk×n为地点特征矩阵，使得 Rm×n=Wm×k⋅Hk×n。NMF求解过程中，假设噪声矩阵为E∈Rm×n且服从高斯分布，则E=R-WH，求解过程就是找到合适的W和H使得‖‖E最小。因为噪声服从高斯分布，那么得到最大似然函数为

假设各数据点噪声的方差一样，使对数似然函数取最大值时，以下目标函数取最小值。

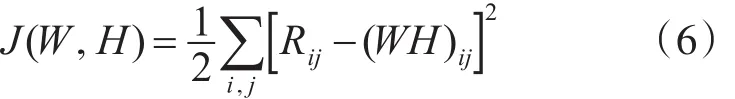
3.3 用户推荐信任度计算

将用户熟悉度和用户兴趣相似度统一起来，得到用户推荐信任度，其计算公式为

3.4 个性化兴趣点推荐

根据协同过滤的思想，基于统一后的用户推荐信任度搜索目标用户u的邻近用户集合Ts（取前S个，S即为邻近用户长度），取集合Ts中用户签到地点集合，去除目标用户u已签到的地点后作为待推荐地点集合L，然后根据邻近用户的签到信息来预测目标用户对为签到地点的偏好程度，计算公式如下：

式（14）中Int（u，i）为目标用户u对地点i的偏好程度，S为邻近用户长度，Tuv为用户v对目标用户u的推荐信任度，Cvi为用户v在地点i的签到次数。根据Int（u，i）的值进行排序，输出前Top-N个地点作为推荐地点。

4 实验分析

4.1 实验数据集

本实验使用Gowalla数据集。Gowalla数据集由 斯 坦 福 大 学 （http：∕snap.stanford.edu∕data∕loc-gowalla.html）提供。该数据集主要包括用户的签到日志记录和用户的好友关系，其中签到数据6442890条，朋友关系数据中节点（用户）有196591个，边（好友关系）950327条。我们抽取了904个用户关于8120个地点的51578条签到数据，稀疏性为99.30%。对每个用户，随机选取80%的签到数据作为训练集，其他的20%的签到数据作为测试集。表1～2分别是Gowalla数据集签到数据、好友关系数据样本。

表1 Gowalla数据集签到数据示例

表2 Gowalla数据集好友关系数据示例

4.2 评测方法

本实验选择查全率（Recall）、查准率（Precision）和F1-Measure作为评价实验结果的评价指标，其中F1-Measure为调和均值，是根据查全率和查准率得到的一个综合指标。计算公式如下：

其中，R（u）为根据训练集推荐给用户u的地点列表，T（u）为测试集中用户u签到过的地点列表。

4.3 实验结果与分析

本文将实验结果与文献［2］中的矩阵特征化MC算法和文献［14］中的奇异值分解SVD算法进行比较。本文提出的基于用户兴趣相似度和熟悉度的算法在后面的图表中用MF表示。我们首先考虑参数α对MF算法推荐结果的影响，将推荐列表长度固定为10，邻近用户数量固定为10，α在［0，1］区间内取值，以0.1的间隔进行递增，图2是参数a取不同值时对应的F1-Measure。可以看到，随着α的增大，F1-Measure的值先逐渐增大，当a为0.4时，F1-Measure值达到最大，说明此时综合推荐效果最佳；当α继续增大时，F1-Measure值逐渐减小。

图2 参数α对推荐效果的影响

图3 是取不同的邻近用户数量S时对应MF算法的F1-Measure值，实验中固定a值为0.4，推荐列表长度N为10，邻近用户长度S在2～16之间取值。从图中可以看出，随着S值得增大，F1-Measure的值逐渐增大，在S取值为10时达到最大值，说明此时的综合推荐效果最佳，随后F1-Measure经历一个短暂的下降后继续缓慢增长并趋于平稳。

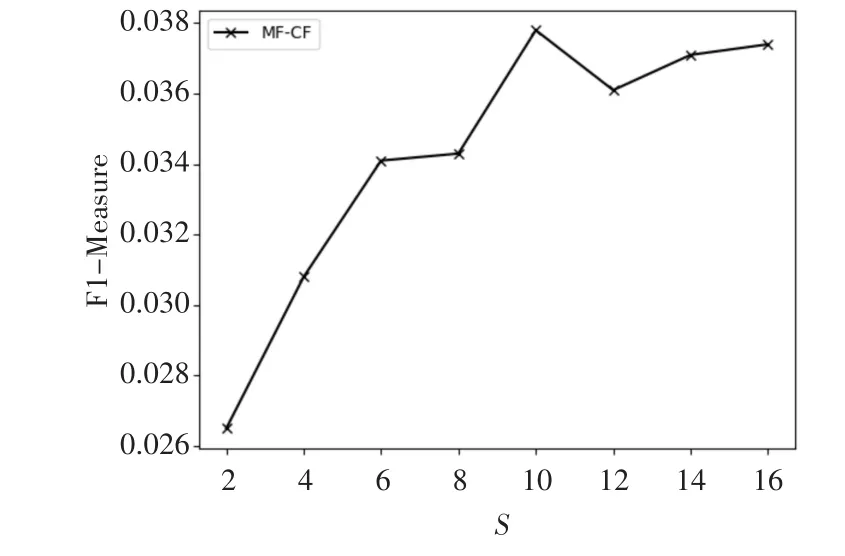
图3 邻近用户数量对推荐结果的影响

图4 Precision指标结果对比

图4 ～6是取不同推荐列表长度N时，各个算法的Precision指标、Recall指标和F1-Measure指标的对比图，实验中固定a值为0.4，邻近用户的长度为10。结果对比显示，当推荐列表长度N取值较小时，查准率较高而查全率较低；随着N值地增大，查准率逐渐下降而查全率逐渐上升；在取不同N值时，MF的各项指标都优于MC算法和SVD算法，说明相较于传统的MC算法和SVD算法，本文提出的算法邻近搜索的效果更佳。主要原因是传统的MC和SVD算法都只是利用了用户的签到信息，未能充分利用社交网络关系数据，所以推荐效果较差；而本文首先利用非负矩阵分解得到用户-特征矩阵，再利用用户-特征矩阵计算用户之间的兴趣相似性，融入用户之间的熟悉度后再进行推荐，这样算法的鲁棒性较好。

图5 Recall指标结果对比

图6 F1-Measure指标结果对比

5 结语

本文提出了一种基于用户兴趣相似度和熟悉度的地点推荐算法。该方法首先根据用户社交网络关系计算用户之间的熟悉度；然后采用非负矩阵分解的方法将用户地点签到矩阵分解成用户特征矩阵和地点特征矩阵，再根据用户特征矩阵计算用户之间的兴趣相似度；最终将用户间熟悉度和兴趣相似度融合成用户间推荐信任度，利用融合后的推荐信任度搜索邻近用户，根据邻近用户的签到信息来计算目标用户对未签到地点的偏好，并选择前Top-N个地点推荐给目标用户。经过实验对比分析表明，本文提出的方法能够获得更加理想的推荐效果。

在以后的工作中，我们将融合多源信息进行深层次的推荐，并考虑推荐地点与目标用户之间的距离，如推荐地点与目标用户活跃区域中心的距离，来调整地点推荐列表中的排序，进一步提高推荐效果。