基于RSSI测距的无线传感器网络质心定位算法优化*

2019-01-02尹亚波

计算机与数字工程 2018年12期

尹亚波徐晴

（洛阳铁路信息工程学校洛阳 471900）

1 引言

传感器节点定位是无线传感器网络的关键技术课题。1992年，剑桥大学定位系统实验室率先从局域定位技术展开探索，在技术方面取得较大成绩，并奠定传感器节点定位理论基础［1］。自20世纪90年代末开始，美国加州大学、日本早稻田大学等相继设立无线传感网络实验室，对相关技术进行理论研究和应用推广。随着研究方法及结果逐渐成熟，为确保节点自定位效果，定位算法也不断系统化［2～3］。当前，AHLOS、Active Badge等传感器定位系统应用范围较广，认可度亦较高。在这些系统中，主要运用的算法有APS、最大似然估计、三边测量以及质心算法等［4～5］。尽管不同算法内部逻辑存在差异，然而基本遵循如下优化步骤：测量未知节点与相邻节点距离；进行算法定位；对定位信息作优化处理［6］。

目前，无线传感技术已取得较大成果，其算法也愈发成熟。然而，各种算法都有其特定适用领域，相互兼容性及转化途径不足。因此，传感系统算法有待继续改进。总结而言，其主要存在定位精度、测距误差、成本较高、能耗不稳定、安全风险、节点移动性以及缺乏应用原型等方面问题或不足［7～8］。基于国内外研究现状，本文拟对无线传感器网络节点定位算法原理、优化进行研究。通过Matlab软件，对算法优化前后效果进行仿真和对比，希望对改进无限传感算法定位精度有积极意义。

2 改进的无线传感器网络节点定位算法

2.1 RSSI的测距原理

相较于测距算法，非测距算法具有可扩展性强、操作性高及运算简单等方面的优点［9］。尤其是质心算法，它不仅具有普通非测距算法的优点，而且具有成本低、使用范围广的特性。然而，在实际应用过程中，质心算法也表现出锚节点密度大、误差较高的不足。因此，有必要运用RSSI技术对质心算法进行优化，在充分发挥其优点的基础上，不断提升其定位精度，降低其成本。

一般来讲，基于RSSI测距技术的无线定位系统包含4个基本步骤，分别是信号发射、信号采集、信号转换以及定位计算［10］。其中，信号转换环节最为关键，它对信号衰减模型准确性有较高要求［11］。在研究过程中，最常用的信号衰减模型是shadowing模型，它包括pass loss模型、遮挡因子这两部分［12］。

pass loss模型表达式为［4］

式中：Pr（d）为距离为d时传感器节点所接收信号的平均能量；Pr（d0）为距离为发射中心参考距离d0状态下传感器节点所接收信号的平均能量；n为路径损耗指数。

由于信号强度单位是dB，因此可将式（1）转化为

遮挡因子是描述信号接收能力变化的随机参数，其单位是dB。将其置入shadowing模型时，可将该模型表达为

在运用shadowing模型过程中，非视距对RSSI影响十分显著。于是，通常会忽略遮挡因子，并将shadowing模型简化如下［13］：

式中：P为距离为d时传感器节点所接收信号强度值；P0为发射中心附近参考距离为d0处传感器节点所接收信号强度值。

运用时，为便于计算，将参考距离d0取值为1.0m。因此，RSSI公式可被简化为

式中：A为距离发射中心1m处传感器节点所接收信号强度值；n为路径损耗指数；RSSI单位为dBm。

依据式（5），可求得d的计算公式为

由式（5）和式（6）可知，参数n、A对RSSI、d的取值有决定性影响，并会进一步影响模型计算精度。如表1所示，A、n取值基于实际情况有特定变化区间。

表1 各种环境下的A、n经验值统计

2.2 迭代式加权质心算法

2.2.1 基于RSSI的加权质心算法

对两个相邻节点，若RSSI越大，表明信号衰减越强，未知节点受测量节点的影响就越大；相反，RSSSI越大，表明信号衰减越弱，未知节点受测量节点的影响就越小。将已知锚节点坐标记为（x1，y2），…，（xn，yn），则可得未知节点D（x，y）的加权质心算法表达式为［14］

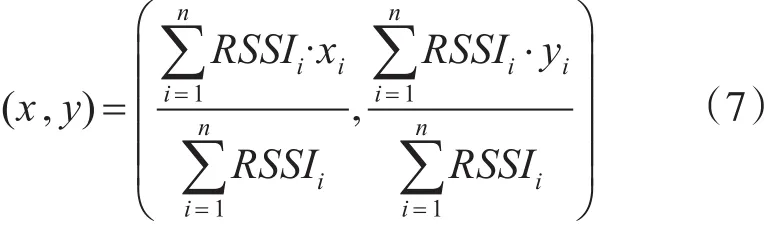
式中：RSSIi为第i个锚节点的信号强度值。

仿真结果表明，在资源既定条件下，相比传统质心算法，该加权质心算法具更佳定位精度。

2.2.2 基于RSSI测距校正值的加权质心算法

为提升质心算法对传播距离等外部环境的调整性能，需要通过实测距离值对RSSI进行校正。将已知锚节点坐标记为（x1，y2），…，（xn，yn），则可得未知节点D（x，y）的加权质心算法表达式为

式中：di为未知节点D与第i个锚节点经测距校正后的距离值。

仿真结果表明，相比RSSI质心算法，该加权质心算法具更佳定位精度。

2.2.3 RSSI迭代式加权质心算法

当锚节点密度较低时，可运用迭代式加权质心算法对已知节点进行迭代升级。基于式（8），迭代式加权质心算法表达式为

式中，qi为第i个锚节点所对应权值调整系数。

2.3 改进的迭代式加权质心算法

由信道传播模型可知，未知节点处RSSI值与锚节点间距呈负相关关系，与未知节点定位精度呈正相关关系。因此，须将RSSI测距值纳入质心算法，以对原算法坐标定位精度进行改进。基于该思路，将式（6）变形可得：

进一步地，可得改进迭代式加权质心算法表达式为

式中，t表示权值系数，其取值随着式（6）中A、n值的变化而变化。

2.4 迭代式加权质心算法权值优化

式（11）中，系数t取值变化较复杂。在运用过程中，需要对其作进一步优化。为求取最优权值系数t，取初始值t=1，以0.10为步长，对区间［0.5，2.5］内各取值作仿真分析。

2.4.1 不同锚节点密度

如表2所示，当锚节点密度由5.0%逐渐增加至10.0%、15.0%、20.0%、25.0%以及30.0%时，最优权值系数t值呈同向增加特征。

表2 不同锚节点密度下的结果

2.4.2 不同定位区域

如表3所示，当定位区域由50m×50m增加至100m×100m、150m×150m时，权值系数t值保持不变。

表3 不同定位区域大小下的结果

2.4.3 不同环境影响

为对整体环境作模拟，本文引入RSSI测距误差λ。如表4所示，由5.0%逐渐增加至10.0%、15.0%、20.0%、25.0%以及30.0%时，最优权值系数t固定为1.9。

表4 不同环境影响下的结果

经过仿真分析可知，权值系数t主要受锚节点密度影响，与定位区域、环境干扰不存在显著相关性。综上，改进的迭代式加权质心算法表达式为

式中：di为锚节点i与未知节点M校正后测距值；qi为锚节点i的权重调整系数。

3 无线传感器网络改进定位算法仿真

3.1 改进算法实现步骤

如图1所示，改进定位算法包含信息广播、测距等4个步骤。其中，在信息广播步骤中，主要完成网络初始化、锚节点信息广播的任务。在误差校正步骤中，须监听锚节点数，并对其误差进行判断；直到将定位计算结果限定在特定区间内，才可进行锚节点标记，并将其升级为已知节点，从而完成优化定位。

图1 改进的迭代式加权质心算法流程图

3.2 同类型算法定位精度仿真结果对比

为明确算法改进效果，在仿真过程中，须将原算法、常见算法与改进算法的定位性能进行对比。

3.2.1 锚节点密度的影响

如图2所示，随着锚节点数目增加，改进迭代式加权质心算法、IWCLA算法以及WCLA算法的平均定位误差均呈显著降低特征。当锚节点数量小于12时，WCLA算法平均定位误差最低；当锚节点数量超过13时，改进迭代式加权质心算法平均定位误差低于另外两类算法。

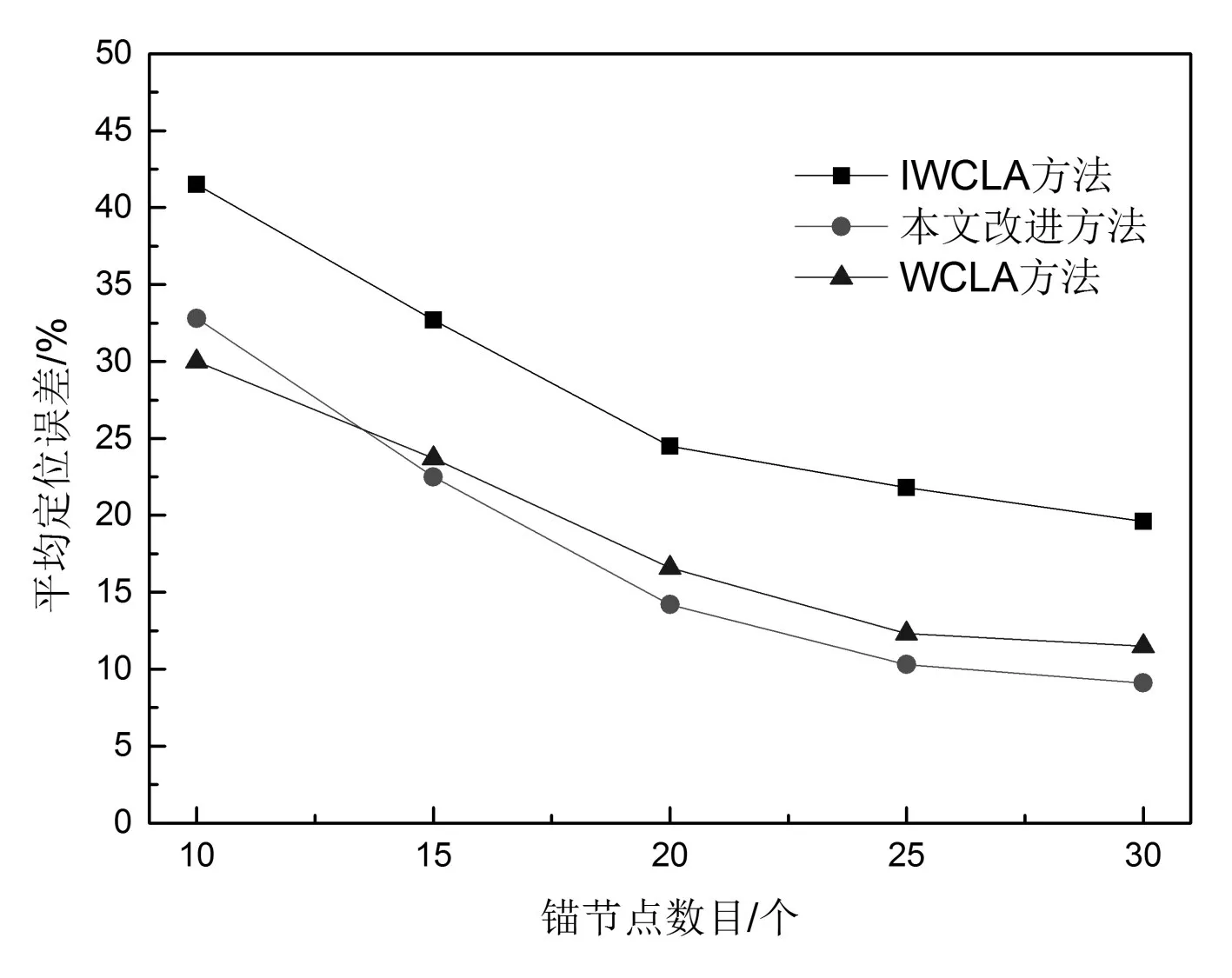
图2 锚节点密度对定位精度的影响

3.2.2 测距误差的影响

如图3所示，随着测距误差增加，改进迭代式加权质心算法、IWCLA算法以及WCLA算法的平均定位误差均呈显著增加特征。当测距误差超过2.0%时，改进迭代式加权质心算法平均定位误差低于另外两类算法；平均定位误差越大，该算法的定位精度优势越明显。

图3 测距误差对定位精度的影响

3.2.3 节点通信半径的影响

如图4所示，随着节点通信半径的增大，各算法下平均定位误差呈显著降低特征。其中，在所有通信半径条件下，改进迭代式加权质心算法的定位误差均值最低；当节点通信半径超过35m时，改进迭代式加权质心算法、WCLA算法所对应的定位误差均值较为稳定，且前者略低于后者。

图4 节点通信半径对定位精度的影响

3.3 不同类型算法定位精度仿真结果对比

在定位精度仿真过程中，选择改进迭代式加权质心算法、AHLoS算法以及DV-HOP算法，从锚节点密度影响等方面对各自定位精度进行对比。

3.3.1 锚节点密度的影响

如图5所示，随着锚节点数目增加，三类算法平均定位误差均呈显著下降特征。当锚节点数目小于6时，改进迭代式加权质心算法的平均定位误差最高；当锚节点数目大于6时，改进迭代式加权质心算法的平均定位误差低于DV-HOP算法、高于AHLoS算法，且下降速度最快；当锚节点数目超过25时，改进迭代式加权质心算法的平均定位误差最低，定位精度达最优状态。