直升机航炮对地面有生力量毁伤的数学模型探讨与修正
2019-01-02周长军肖慧鑫吴小役杨健为
周长军,肖慧鑫,吴小役,杨健为,李 勇,张 龙
(1.西北机电工程研究所,陕西 咸阳 712099;2.国防大学研究生院,北京 100091)
航炮是武装直升机的主配武器之一,可以用于对地面目标打击以及直升机空战。直升机载航炮武器系统可攻击的地面目标包括步兵班,火力点,仓库,雷达站,指挥所,通信站和轻型车辆等[1]。评估航炮武器对地面目标的毁伤效果,是航炮设计过程中的重要环节[2]。笔者主要探讨武装直升机航炮对地面有生力量的毁伤能力计算方法。
针对地面有生力量毁伤能力计算,已往文献对地面毁伤模型做了一定的研究,但笔者认为相关结论并不适用于航炮毁伤分析。文献[3]在确定破片飞散角时,未考虑人员的高度,将人员简化为一个点,因此在进行空炸引信杀伤计算时,炸高从0增大,杀伤能力单调下降,这与实际规律矛盾,为此,笔者提出了新的破片飞散角计算模型。文献[4]计算空炸射击目标的受弹面积时,对于定积分进行了近似处理,按照处理后的数学表达式进行计算,结果是受弹面积随炸高而增大,笔者采用新的方法,对定积分数学表达式不再进行近似处理,而是直接在MATLAB中进行编程计算,利用MATLAB的强大计算能力直接计算定积分,避免了近似处理带来的问题。文献[4]在确定椭圆毁伤律参数时,建立了空炸射击毁伤的计算模型,按照其空炸射击模型编程计算,结果明显不正确。笔者从等效参数计算的基本概念出发,提出了新的椭圆毁伤律参数计算模型。
笔者对上述3个关键环节的深入分析与模型修正,均未见于其他文献。
1 误差分析
为了描述射击误差,定义如下坐标系:以目标中心为原点O,x轴表示纵向,沿射击方向为正;z轴表示横向,朝右的方向为正,如图1所示。图1中,点A为射击指向点,记为(x0,z0),对应瞄准误差;点C为落点散布中心,其对点A的误差(xn,zn)为诸元误差;点P为炸点,其对点C的误差(xp,zp)为散布误差。
射击时,某次发射的弹药,由于存在弹道散布,弹着点是随机分布的。炸点对目标中心的误差,也即射击误差为(x,z)。
X=Xn+Xp+X0
(1)
(2)
(3)
式中,X、X0、Xn、Xp分别为射击误差、瞄准误差(一般情况下不予考虑)、诸元误差、散布误差。
在射击中,诸元误差、散布误差为随机量且相互独立,并且它们都是二维正态变量,期望值为0,协方差记为∑n和∑p。它们对应的分布为[2]:
(4)
(5)
射击误差的分布为:
(6)
其中,协方差阵为
∑=∑n+∑p
(7)
2 破片毁伤有关计算方法
2.1 破片飞散角及射击条件下的破片初速确定
设炸点对目标的坐标为(x,y,z),人员的躯干高为a,宽为b,厚为c,炸高为h,弹丸的落角为θ、末速为vc,爆炸时破片所获得的速度为v0。在图2中,x轴是纵向轴,z轴是横向轴,y轴是高度轴,点P为炸点,点A为人在高度方向的中心点,矢量vc为弹丸落速的方向,R是炸点对目标中心的距离。
破片命中目标时的飞散角β′为
(8)
(9)
式(8)和式(9)对文献[3]的相应表达式进行了修正,考虑了人员的高度。
破片命中目标时的飞散角为β′,则相应的静态飞散角β为
(10)
(11)
2.2 命中目标的破片平均数
根据静态飞散角β,可以得出其相对应的球带,此球带的界限角设为(β1,β2),并有:
β1≤β≤β2
考虑到弹丸具有向前的速度vc,动态界限角与静态界限角的关系为
(12)
(13)
并有


(14)
假定炮弹破片总数为N,则落入区域Ω中的破片数为NC,C为静态时在界限角β1、β2中的破片百分数,因此命中目标的破片平均数为
式中,ν为目标的受弹面积。
2.3 破片数目随散飞方向的分布规律
破片飞散密度分布函数[5]
(15)
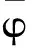
2.4 破片与目标碰撞时存速
破片飞到距离R的速度
(16)
式中:vR为距爆心R处的破片速度,m/s;v为破片初速,m/s;α为破片速度衰减系数;A为破片迎风面积,m2;m为破片质量,kg;CD为破片阻力系数,取值1.24;φ为破片形状系数,取值3.2×10-3;ρa0为海平面的标准空气密度,取1.225 kg/m3;ρa为空气密度,kg/m3;H(y)为空气密度随海拔高度的修正系数。
2.5 目标的受弹面积
目标的受弹面积与目标的姿态和朝向有关,目标的受弹面积取目标不同朝向时的受弹面积的平均值。设目标朝向角服从均匀分布,分布密度为
(17)
式中,r为目标朝向角。
设b1、c1分别为目标朝向角为r时目标的等效宽度和厚度,则:
(18)
(19)
对于空炸射击,当炸高h小于或等于目标的高a时(h≤a),有
(20)
(21)
对于空炸射击,当炸高大于目标的高a时(h>a),有
(22)
由于以上的计算表达式无法人工手动计算,文献[4]对定积分进行了近似处理,但是按照近似处理后的数学表达式进行计算,发现受弹面积随炸高而增大。笔者采用新的方法,对于空炸射击,目标受弹面积表达式中含有的定积分求解,可以利用MATLAB软件中的定积分函数进行计算,而无须对表达式进行近似处理[6]。
对于空炸射击,当炸高h=0时,则为着发射击时的受弹面积。
2.6 椭圆毁伤规律参数
决定椭圆毁伤律的参数ηx、ηz,应使曲面Gη(x,z,h)与G(x,z,0)较大程度的一致,h>0时为空炸射击,h=0时为着发射击。
按照文献[4]空炸射击模型编程计算时,毁伤的计算结果明显不正确。针对文献[4]空炸射击模型存在的问题,笔者从等效参数计算的基本概念出发,提出了新的椭圆毁伤律参数计算模型。
令:


有
解方程组得到:
(23)
(24)
3 算例
采用笔者提出的修改后的计算模型,对某30 mm弹药杀伤有生力量的能力进行计算。目标分布及射击条件参照美国阿帕奇30 mm航炮对有生力量的毁伤计算,即对人员杀伤,8名士兵稀疏分布,士兵间隔距离不小于1 m,理想的瞄准点位于目标区域的中心。取理想的瞄准点位于坐标(0,0),8名士兵的坐标分别为M1(6 m,6 m)、M2(6 m,0 m)、M3(6 m,-6 m)、M4(0 m,6 m)、M5(0,-6 m)、M6(-6 m,6 m)、M7(-6 m,0 m)、M8(-6 m,-6 m),人员的躯干高a为1.5 m、宽b为0.5 m、厚c为0.2 m。点射长度分别取5、10、20发。
通过计算,得到不同射弹量对距离1 000 m处8个立姿稀疏目标杀伤的数学期望计算结果,如表1所示。

表1 对1 000 m立姿稀疏目标杀伤的数学期望
从计算结果可以看出,炸高在1.0 m时对人员的毁伤概率最大,和定性分析的规律一致。
4 结束语
笔者针对武装直升机航炮对地面有生力量的杀伤能力进行了研究,在确定破片飞散角计算时,建立了新的计算模型,计算模型考虑了人员的高度;在计算空炸目标受弹面积时、提出利用MATLAB软件强大的计算能力进行定积分计算,消除了对计算模型进行近似处理所带来的问题;在确定椭圆毁伤律参数时,建立了新的计算模型。在解决了参考文献存在的以上3个问题之后,对地面有生力量的杀伤计算可较真实地反映武装直升机航炮实际的毁伤能力。
笔者提出的破片飞散角计算模型,目标受弹面积计算方法、椭圆毁伤律参数计算模型同样适用于其他各类火炮对地面有生力量的杀伤计算。
