一种新的广义二次相关时延估计算法

朱 超，屈晓旭，娄景艺

(海军工程大学，湖北 武汉 430033)

0 引 言

时延作为表示信号特征的一个重要参数，随着信息通信技术的飞跃式发展，时延估计在信号处理领域成为人们研究的热点问题。基本时延估计要解决的问题是对2个接收目标信号进行处理，准确快速地估计和测量接收信号之间因信号传输过程中通道的不同而引起的时间延迟[1]。广义互相关(GCC)时延估计是一种最基本、最常用的时延估计方法，该方法是利用加权函数来增加信号的有用成分，锐化了相关函数的峰值。根据其加权形式和准则的不同，有ROTH加权、SCOT加权、PHAT加权和HB加权等广义相关时延估计方法[2]。在以上加权方法中，HB加权的广义互相关时延估计性能可以达到克拉美罗界。但在低信噪比环境中，由于干扰噪声的影响，广义互相关方法的时延估计性能会急剧恶化。而二次相关时延估计算法可以利用二次相关来有效抑制噪声的干扰进而提高抗噪声性能，但二次相关时延估计的时延精度还有待提高。为此，本文基于广义互相关时延估计和二次相关时延估计，同时利用希尔伯特变换具有把偶函数转变为奇函数的特点进行相关希尔伯特差值法运算，实现对2个接收信号二次互相关函数峰值的锐化处理，改善了二次互相关函数峰值点的检测效果，增大了时延估计的精度。本文分别比较了传统互相关算法、二次互相关算法和本文提出的算法在时延估计的准确性和平稳性。仿真实验结果表明，本文提出的新算法在低信噪比环境下的时延估计性能有了明显的改善。

1 基本时延估计信号模型

在进行接收信号的基本时延估计前，首先要给定2个接收信号的模型。互相关(CC)是用来比较2个信号或函数在时域相似程度的基本方法。时延估计算法可以通过以下2个信号模型来分析：信源发射信号s(t)经2个传输通道过程中加入了噪声的信号x1(t)和x2(t)。设信号x1(t)和x2(t)满足以下方程：

(1)

式中：A1和A2为发射信号的幅度参量，表示s(t)经不同通道传输后的幅度增益和相位偏移；n1(t)和n2(t)代表未知的加性平稳高斯白噪声；τ1和τ2表示信号传输的时延，且τ1≤τ2。

为表达方便，以x1(t)为标准进行归一化，则式(1)可以重新表示成：

(2)

式(2)离散形式表示为：

(3)

式中：k=0,1,…,N-1；λ=A2/A1，表示2个接收信号的幅值比；D=τ2-τ1，表示所求时延值；N表示采样点数。

2 基本时延估计算法分析

2.1 广义互相关法

广义互相关(GCC)时延估计是一种经典的时延估计方法，其利用加权函数来增加信号的有用成分，通过计算2个接收信号的互相关函数峰值得到时延值[3-5]。其基本原理如下：x1(t)和x2(t)的互相关函数表示为：

R12(τ)=E[x1(t)x2(t+τ)]=

λRss(τ-D)+Rsn2(τ)+

λRn1s(τ-D)+Rn1n2(τ)

(4)

假设n1(t)和n2(t)是独立于s(t)平稳不相关的高斯白噪声，则2个噪声n1(t)、n2(t)与信号s(t)的互相关函数为：

Rn1s(τ-D)=E[n1(t)·s(t+τ-D)]=0

(5)

Rn2s(τ)=E[n2(t+τ)·s(t)]=0

(6)

噪声n1(t)与n2(t)的互相关函数为：

Rn1n2(τ)=E[n1(t)·n2(t+τ)]=0

(7)

则：

R12(τ)=λRss(τ-D)，-∞<τ<+∞

(8)

由自相关函数|Rss(τ)|≤Rss(0)的性质可知，当τ=D时Rss(τ-D)最大，即R12(τ)也达到最大。因此，求得R12(τ)的峰值对应的τ就是2个接收信号之间的时延。

为了克服基本互相关时延估计中易受环境噪声影响的缺陷，广义互相关时延估计算法利用加权函数增强了信号中信噪比的作用，从而提高了时延估计精度[6]。在此基础之上，通过频域加权函数对信号进行前置滤波，尽量抑制噪声的干扰，然后对加权后的函数进行互相关运算，获得其峰值。

根据维纳-辛钦定理可知，互相关函数与其互功率谱密度互为傅里叶变换对，则x1(t)和x2(t)的互相关函数又可以表示为：

(9)

式中：G12(ω)为x1(t)和x2(t)的互功率谱函数。

当x1(t)和x2(t)经过滤波之后，输出信号的互功率谱函数可以写为：

(10)

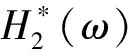
所以，信号x1(t)和x2(t)的广义互相关函数可表示为：

(11)

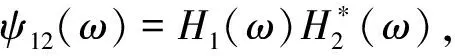
在时延估计过程中，可以通过选取不同加权函数来针对不同类型的干扰噪声进行适当的滤波处理，使噪声干扰的影响得到有效抑制[7]，然后会使得R12(τ)有一个峰值相对较大、较尖锐，其对应的横坐标即为所求时延，从而提高时延估计精度。Hassab和Boucher在期望信号峰值与输出噪声之比为最大的准则下，导出了HB加权函数[8]。利用HB加权的广义相关时延估计算法可以达到克拉美罗界，在实际应用中具有较好的性能。

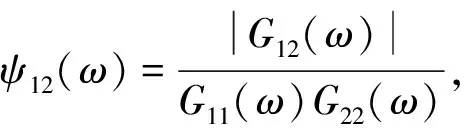
2.2 广义二次相关法

在广义互相关时延估计算法的基础上，广义二次相关法是广义互相关时延估计算法的改进，该算法先对2个接收信号进行互相关运算，再对其中一个接收信号进行自相关运算，然后利用得到的互相关和自相关函数，再进行第2次互相关运算，以提高信号的抗干扰能力[9-13]。信号x1(t)的自相关函数为：

R11(τ)=E[x1(t)x1(t+τ)]=

Rss(τ)+Rsn1(τ)+Rn1s(τ)+Rn1n1(τ)

(12)

2个接收信号的互相关函数为：

R12(τ)=E[x1(t)x2(t+τ)]=

λRss(τ-D)+Rsn2(τ)+

λRn1s(τ-D)+Rn1n2(τ)

(13)

假设忽略信号和噪声的互相关函数，噪声为非相关的高斯白噪声。根据白噪声的自相关数学特性，Rn1n1(τ)在τ=0处为冲激函数，在信噪比低的情况下需要考虑其影响，在τ≠0时幅度会剧减，可以忽略其影响。由于R11(τ)和R12(τ)依然是时间的函数，对R11(τ)和R12(τ)再做互相关，即可得到二次相关函数：

RRR(τ)=E[R11(t)R12(t+τ)]

(14)

将式(12)和式(13)代入式(14)中得到：

RRR(τ)=λRss(τ-D)+Rn1n2(τ)

(15)

式中：Rss(τ-D)表示信源发射信号做二次互相关；Rn1n2(τ)代表噪声做二次互相关。

同广义互相关法一样，根据相关函数的特性，当τ=D时Rss(τ-D)取最大值，因此找出其峰值，峰值横坐标所对应的位置即为所求时延值。

2.3 相关希尔伯特差值法

为了在相关函数峰值较为平坦时，使时延估计也能准确进行，根据对希尔伯特变换的定义和性质的了解，利用奇函数的希尔伯特变换是偶函数，偶函数的希尔伯特变换是奇函数的性质，可以把经典的广义互相关时延估计算法中峰值检测处理互相关函数用过零点检测来代替[14-15]。希尔伯特变换时延估计在一定程度上降低了干扰噪声对信号时延估计准确度的影响，但是当处在复杂环境时，信源发射信号受到噪声和其它干扰的影响较大，时延估计值在信号波形中对应的零点附近很大可能会出现波动现象，因而出现了多个过零点情况，就会很难判断出时延估计值对应的真正零点，导致时延估计误差增大。而且，当信号序列长度较长时，也会出现多个过零点情况，必须采用其它的算法加以辅助改善。

针对上面的情况，相关希尔伯特差值法的提出有效地解决了这一问题。相关希尔伯特差值法的定义就是将互相关函数与其希尔伯特变换后的函数的绝对值做差处理，即：

(16)

相关希尔伯特差值法既保留了峰值附近的值，又使峰值外其余部分值的相关性减小了，从而使接收信号相关函数波形的主峰值尖锐程度明显增加。相关希尔伯特差值算法不但起到提高时延估计精度的作用，而且算法简单，易实现。

2.4 新算法原理

总结了HB加权广义互相关时延估计和二次相关时延估计算法各自的优点与不足，在二者的基础上，同时利用相关希尔伯特差值法，本文提出了一种新的广义二次相关时延估计算法，称之为HB加权广义二次相关希尔伯特差值时延估计算法。新算法流程图如图1所示，()*表示取共轭运算，|·|代表取绝对值。

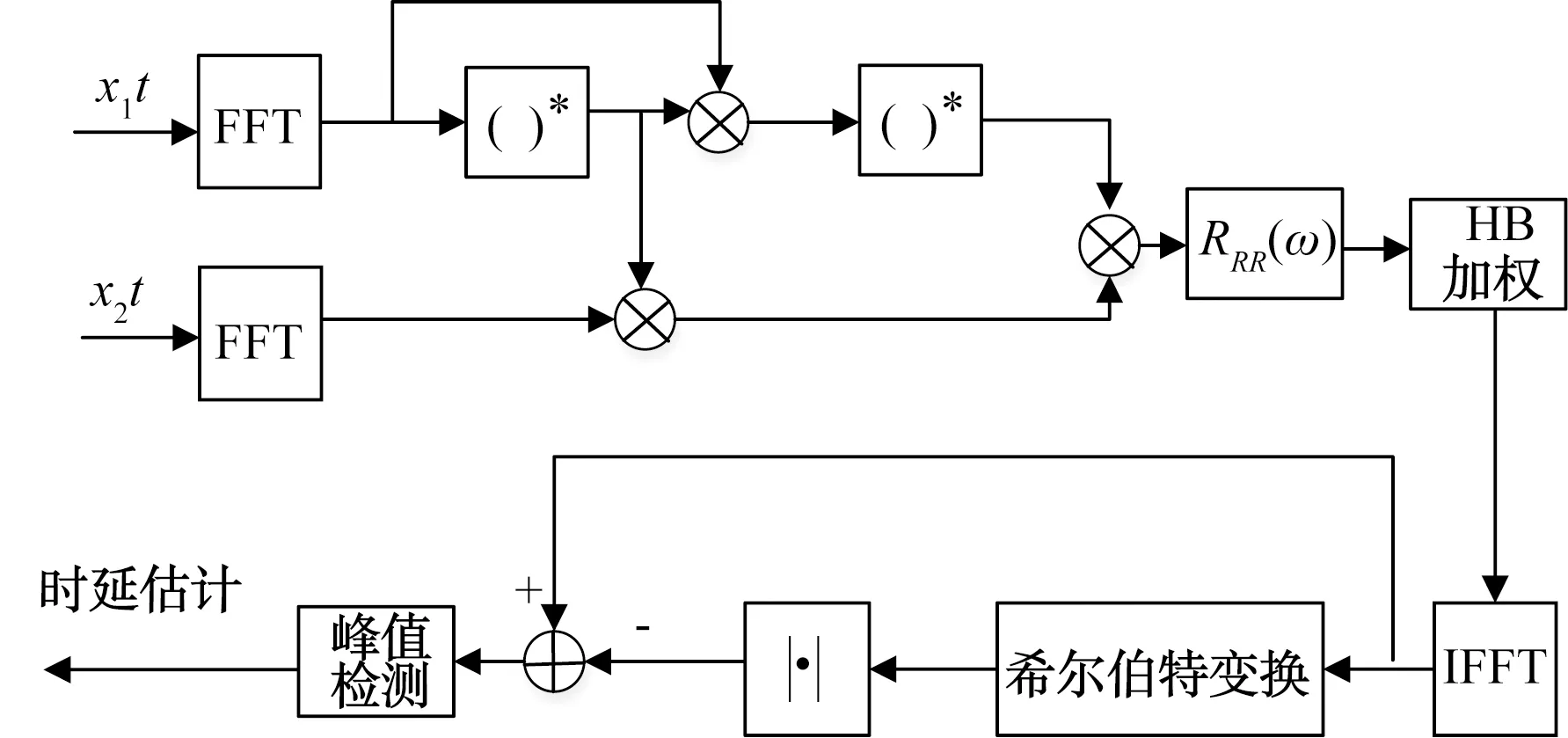
图1 新算法流程图

与传统互相关算法不同的是，在功率谱密度函数进行加权处理以前，新算法首先对接收信号x1(t)和x2(t)进行快速傅里叶变换，减少了互相关算法计算处理的时间，提高了算法的实时性，然后将得到的信号自相关与互相关看作新的信号，进行二次相关处理，从而得到二次相关互功率谱RRR(ω)函数，大大减少了噪声对信号的影响，接着HB加权处理增加了接收信号功率谱密度中的信源发射信号成分，然后进行快速傅里叶逆变换，再利用希尔伯特差值法锐化互相关函数的峰值，达到提高时延估计精度的目的，最后对得到的HB加权广义二次相关希尔伯特差值序列进行峰值检测，就获得了时延估计值。

3 仿真与分析

为了验证新算法的时延估计性能，下面通过MATLAB首先仿真了二次相关法，然后对新算法和HB加权广义互相关时延估计算法在不同信噪比环境下进行仿真对比说明。仿真构造了加有平稳高斯白噪声的2个通道接收信号，仿真中采用的接收信号幅度为10，频率为1 kHz的单频正弦波信号，采用采样频率为50 kHz，采样点数为1 024，对2个通道接收到的信号进行采样。假设2个信号之间的延迟为100个采样间隔，即延迟时间τ=2 ms的正弦波来仿真模拟2个不同通道的接收信号，其中噪声是平稳高斯白噪声。假设信号与噪声、噪声与噪声都是相互独立的，σSNR1和σSNR2为接收信号的信噪比，信噪比(SNR)的定义为σSNR=20lg(σs/σn)，其中σs和σn分别是信号和噪声的标准差。当σSNR1=5 dB，σSNR2=15 dB时，二次相关法的时延估计仿真结果如图2所示，在信噪比σSNR1=5 dB，σSNR2分别为15 dB、5 dB、-5 dB和-15 dB的环境下，HB加权广义互相关时延估计算法的仿真结果和新算法的仿真结果分别如图3、图4、图5和图6所示。

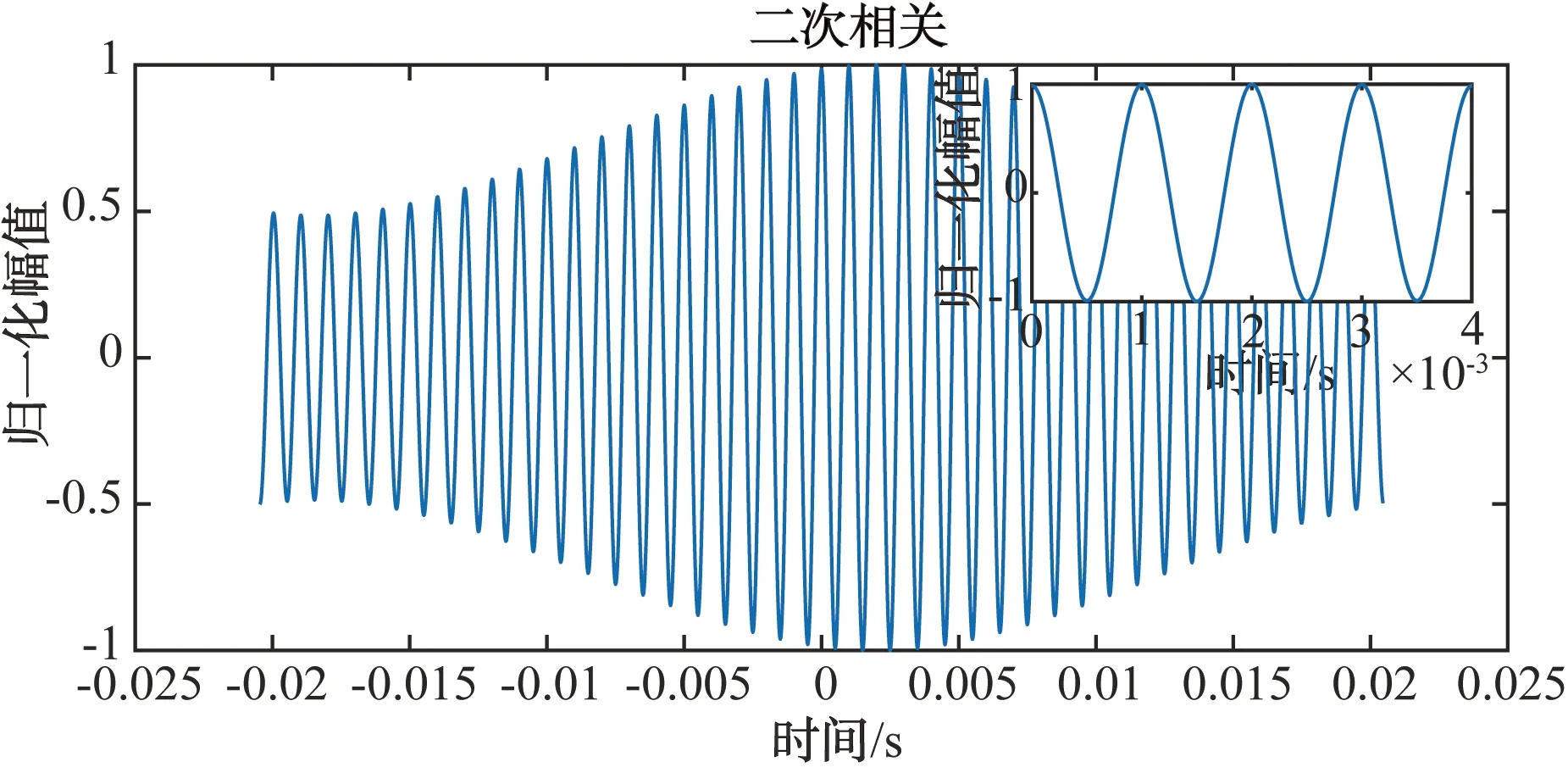
图2 σSNR2=15 dB时二次相关法的仿真结果

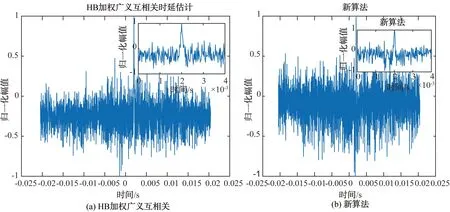
图3 σSNR2=15 dB时的仿真结果

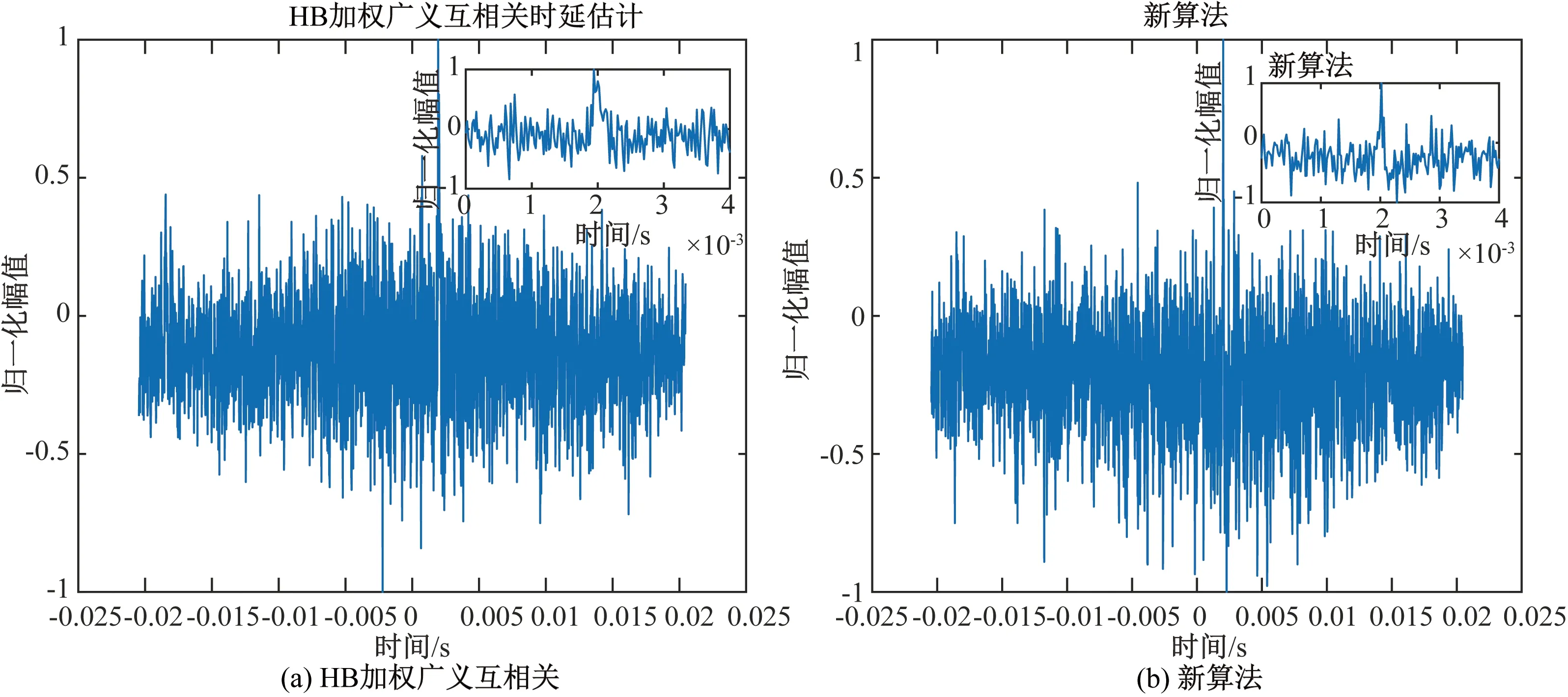
图4 σSNR2=5 dB时的仿真结果

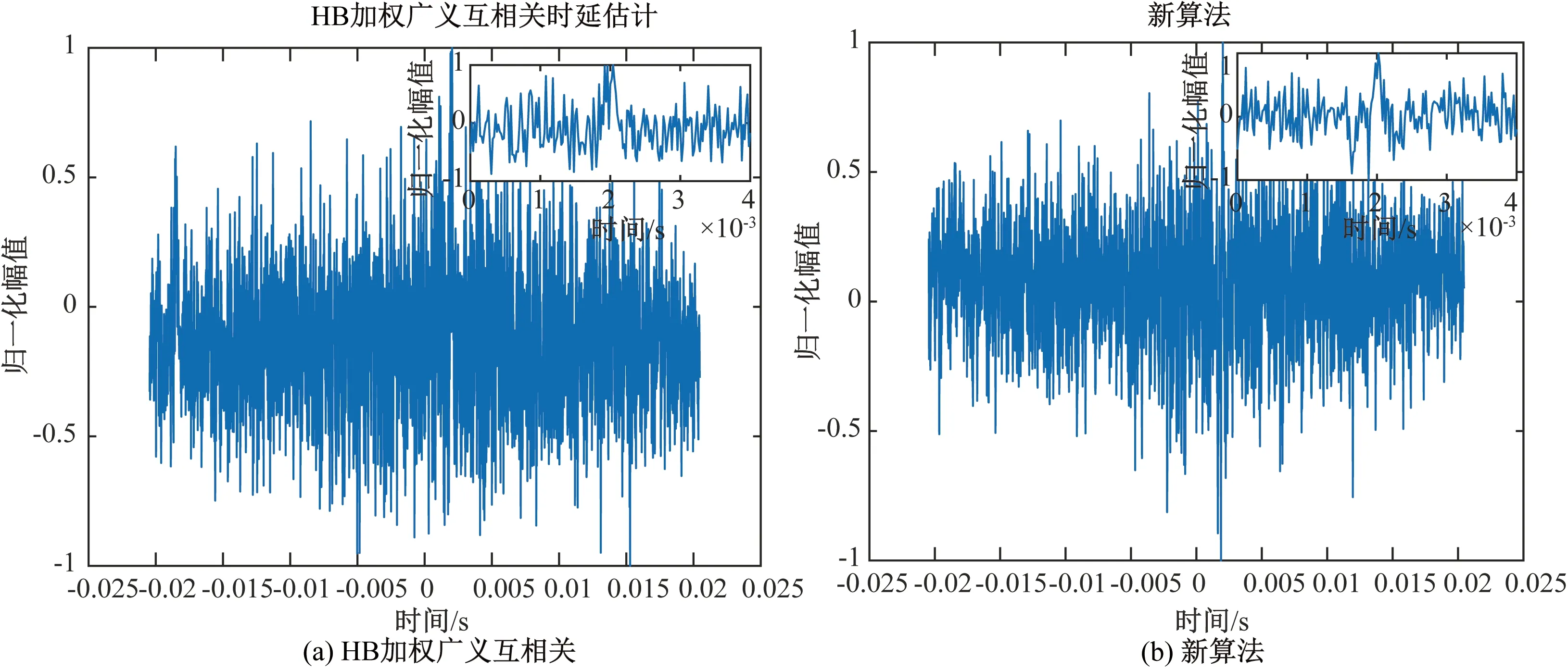
图5 σSNR2=-5 dB时的仿真结果

对比图2和图3可以看出，在信噪比σSNR1=5 dB，σSNR2=15 dB时，二次相关法的相关函数峰值受周期信号影响较大，峰值不明显，而HB加权广义互相关和新算法都具有锐化相关函数峰值的作用，信号相关函数的峰值都比较尖锐，时延估计效果也差别不大，都能准确估计出时延值。从图4中得知，在信噪比σSNR1=σSNR2=5 dB时，新算法相比较于HB加权广义互相关法的相关函数的峰值更加尖锐，具有较好的时延估计精度。从图5和图6中来看，随着信噪比σSNR2的降低，HB加权广义互相关法的时延估计峰值受噪声的影响变化变大，在信噪比σSNR2=-15时，其时延估计峰值几乎淹没在噪声之中，甚至无法进行有效的时延估计；而新算法随着信噪比σSNR2的下降，虽然时延估计性能有所下降，但还保持着较尖锐的相关函数峰值，具有一定的抗干扰能力，达到在低信噪比环境下仍可获得较为准确的时延估计值的需求。

为进一步验证所提算法的时延估计的有效性，下面对3种不同时延估计算法的性能进行仿真实验，比较不同算法在信噪比σSNR2从-20 dB到10 dB时的均方根误差(RMSE)，均方根误差定义为：

(17)

式中：τ0为真实时延值；τi为第i个时延估计值；N为时延估计总数。

本文进行N=30的仿真实验，仿真结果如图7所示。

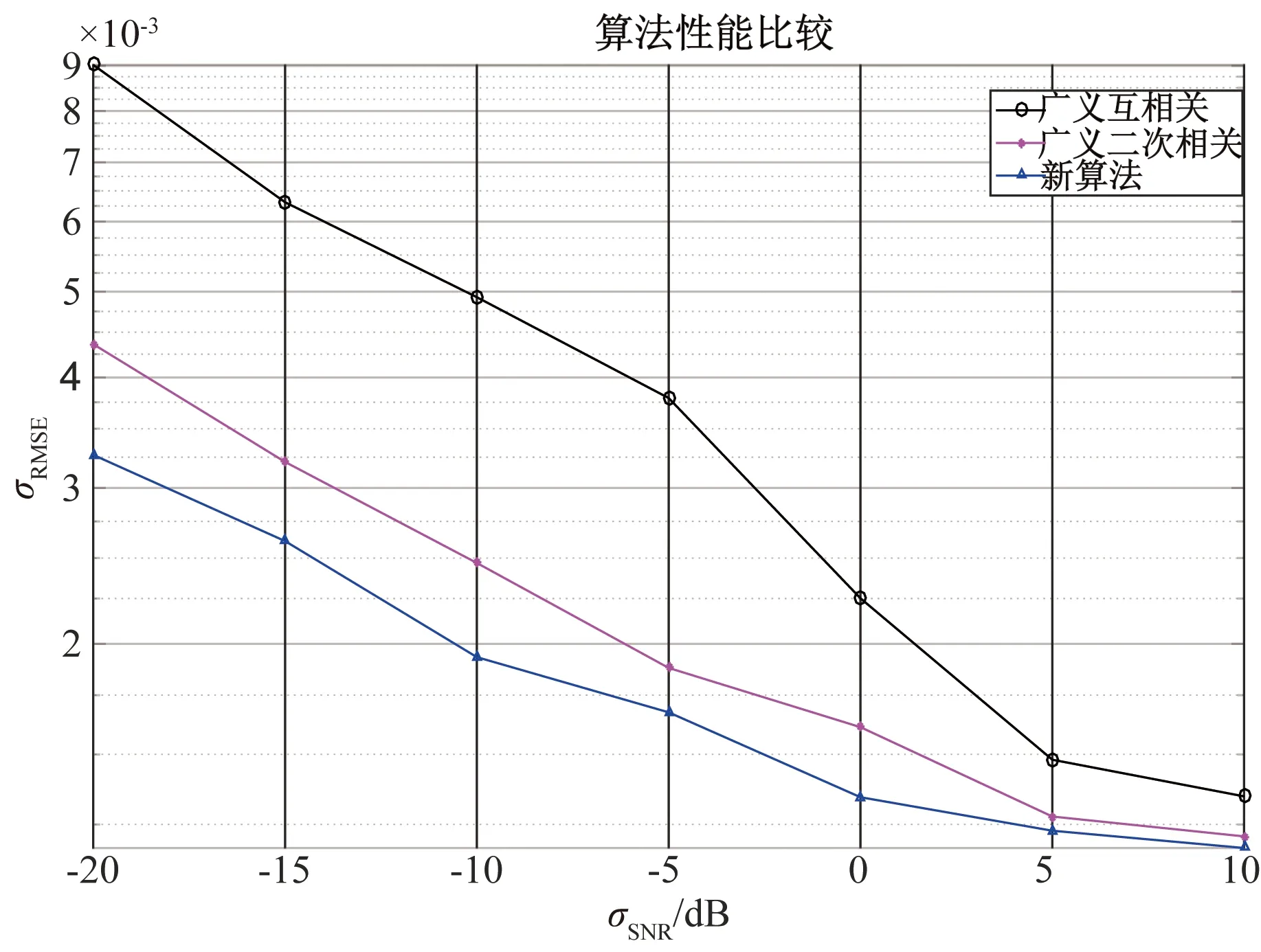
图7 不同算法估计性能比较仿真结果

从图7中仿真结果可知，随着信噪比的降低，3种算法的均方根误差RMSE都会变大。在信噪比从0～10 dB时，3种算法的估计性能差别不大；从-20～0 dB时广义互相关算法和广义二次相关算法的RMSE会随着信噪比的降低而迅速变大，而新算法变化较为缓慢，仍具有较好的时延估计性能。无论信噪比大小，新算法都比另外2种算法具有更好的时延估计性能。

4 结束语

结合广义互相关时延估计和二次相关时延估计的优点，同时利用希尔伯特变换的性质，本文提出了一种HB加权广义二次相关希尔伯特差值时延估计算法。在低信噪比下，新算法在时延估计的准确性和平稳性方面比HB加权广义互相关算法表现出更好的特性，时延估计性能有了明显的改善。