离散选择试验中试验设计步骤的实现—基于SAS宏程序的应用*

刘仲琦 郝 春△ 顾 菁 郝元涛

离散选择试验与试验设计

离散选择试验(discrete choice experiment,DCE)是基于经济学的需求理论和效用理论进行研究的,最初应用于经济学、市场营销领域,近十几年被越来越多地应用到卫生领域。DCE在卫生领域中的应用主要有两方面，一是在卫生人力政策研究中的应用,主要用于测量卫生服务人员的工作意愿[1-3]。如国内有研究者运用DCE研究乡镇卫生院护理人员的工作偏好,发现月收入、继续教育机会和住房是影响护理人员工作意愿的前三位因素[1]。二是在卫生服务利用的研究中,应用离散选择实验的方法研究目标人群对某项卫生服务的使用偏好或需求。如利用DCE研究人们对于大肠癌筛查的意愿偏好[4]或用于研究居民对服务提供者的选择偏好[5]、疫苗接种偏好及需求等[6-7]。

DCE假设某项商品或服务可以由几个特性(如月收入、工作负荷等)进行描述,每个特性可以定义不同的水平(如报销比例的水平可为30%、60%、90%),根据几种特性不同水平的变化,可组合成一系列假设的选择集问卷。由受访者通过对选择集中的替代方案做出选择,而这些选择结果被假设为是受访者经过权衡后,认为能对其产生最大效用的选项。通过整理和统计分析,可以定量分析出服务或商品的某一特性对受访者选择意愿的影响程度,从而体现出受访者从自身角度出发的意愿、偏好[8-10]。

与一般常用的单因素和多因素分析研究影响意愿的因素的方法不同,DCE通过设计选择集,模拟一个合理、直接、近似现实的决策权衡过程,从而定量测量受访者接受服务前的自述偏好，即从患者自身的角度出发,通过受访者自身的理解和权衡其所需的医疗服务的效用价值,以便卫生政策制定者与医疗服务提供者明确了解“消费者”的需求。另一方面,DCE中纳入的属性和水平既可以是实际存在的,也可以是根据政策设想而设计的,但传统的影响因素调查只能基于现实条件,说明了DCE能更真实准确地反映受访者的需求和意愿。此外,若属性中包含有连续型变量,可以由此测量各个属性之间的替代关系。如个人愿意为一个较近的社区医院而多花费的价钱等[6,11]。

DCE的实施步骤主要包括:(1)确定研究因素及各因素不同水平的设置。(2)试验设计,即将不同因素的各个水平组合成不同的选项方案,然后每两个或多个选项方案组合成一个选择集,最终形成有多个选择集的选择试验问卷。(3)数据收集整理。(4)数据分析与解释。确定研究因素及各因素不同水平的设置和试验设计是DCE实施的两个关键步骤[3,12]。

本文主要基于SAS 9.4宏程序介绍DCE中试验设计步骤的实现。

试验设计的原理

确定了研究因素和相应的水平后,各个因素和水平将被整合成不同选项方案。研究者将向研究对象逐一展现这些选项,并让他们从中做出选择。试验设计关注的内容就是如何以统计学有效的方式将各个因素的水平组合成不同的选项,并最终形成选择集[3,11-12]。

总的来说,试验设计的方法可以分为完全因子设计和部分因子设计。完全因子设计包含各个因素所有水平的组合,它的优点是可以估计所有因子的主效应、两两交互效应、以及更高阶的交互效应。但是,在实际研究中,完全因子设计会产生大量的选项。因此,实际应用中通常只选择所有可能组合的一部分进行试验,即部分因子设计[11]。

部分因子设计(factional factorial design)是指从完全因子设计中挑选一部分组合来进行数据收集。而仅取一部分的代价是,在部分因子设计中,一些效应会被混杂。例如,在市场研究中,最常用的是分辨度Ⅲ的部分因子设计,在该设计中,各个主效应不与任何其他主效应混杂,但是可能与二因子交互作用混杂。在部分因子设计中,最常用的是正交设计和D-optimal设计[11,13-14]。

正交设计是在早年的DCE研究中应用较多的一类部分因子设计。它是基于正交表设计的,具有正交、平衡的性质。正交性是指两因素之间相关性较低或为零,表现为任意两个因素的所有水平对在整个试验设计中出现的次数相等或者成比例。平衡是指每个因素的各个水平在整个试验设计中出现的次数相同,例如,假设有一个2水平的因素A,在正交设计中,两个水平出现的次数各为50%。一个4水平的因素B,它的4个水平在正交设计出现的次数各为25%。Huber和Zwerina提出,一个好的试验设计除了要具备正交、水平平衡的性质外,还要做到最小重叠,即在每个选择集内因素水平重复的概率要尽可能小[15]。

但近年来,从统计学角度出发研究的更有效的试验设计得到发展[11]。这一类的设计称为D-optimal设计。这类设计的目的是牺牲一定的正交性,使得自变量的协方差矩阵的行列式最小化,即通过参数的标准误最小化来确保参数估计值的变异最小化,从而使得模型的参数估计精确度更高[11,15-16]。假设在一个试验中有i个因素,x1,…,xi,则y与各因素间的关系可以表示为y=β1g1(x1,…,xi)+…+βmgm(x1,…,xi)+ε

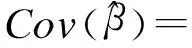
SAS宏程序

SAS 9.2以上的版本可以使用宏程序实现DCE的试验设计，最常用到的宏程序之一是%ChoicEff。这个程序可以为选择试验寻找有效的试验设计,并可对设计进行评价。%ChoicEff采用调整的Fedorov备选集寻找算法。首先向宏程序提供一个完全因子设计或部分因子设计或从%MktEx宏程序产生的正交设计作为备选集。然后%ChoicEff宏将从备选集中随机构建一个初始设计(也可指定初始设计)。接着程序会用备选集中的每个方案去替换初始集中的每个方案,只有能够提高试验设计效率的交换才会被执行。这个过程会持续直到设计功效稳定在最大值,最后输出最优设计[16]。试验设计的效率通常用D-efficiency和相对D-efficiency来衡量。D-efficiency是信息矩阵的逆阵的行列式的几何均值，其值会随设计过程中对因素水平的编码方式不同而不同。因此,有相对D-efficiency这一指标。相对D-efficiency为两种设计方案的D-efficiency的比值,用以比较两种试验设计方案。也有部分文献直接将D-efficiency定义为两个设计的信息矩阵的行列式之比[17]。

示 例

本文采用WHO的DCE应用指导书中的例子,来展示利用SAS宏程序实现选择试验中试验设计步骤。

该例子是在坦桑尼亚进行的关于卫生人力资源的研究。坦桑尼亚在实现向大部分人口提供关键卫生服务这一目标时,所面临的严重问题是卫生人员的地域分布不平衡。为此,设计DCE的研究目的是:(1)探索临床工作人员在工作选择时工作的不同属性的影响。(2)探索受访者在这些属性之间的权衡,即“受访者愿意放弃多少薪水来获得其他因素的改进？”。希望以此为政策制定者提供有价值的信息,考虑不同的激励措施,为农村偏远地区招募更多卫生工作者。经过前期的文献综述和对临床学生进行半结构化深入访谈,最终确定了7个纳入研究因素,其中3个4水平因素,4个2水平因素[11]。如表1所示。

表1 坦桑尼亚研究中的因素和其水平

根据所确定的因素与水平,如果实施完全因子设计,将产生43×24=1024个可能的工作组合。若将这些组合两两配对成一个选择集,则将产生(1024×1023)/2=523776个选择集。因此,我们采用部分因子设计,利用%ChoicEff宏程序来创建一个含16个选择集,每个选择集里有2个备选方案的选择设计。

首先,%MktRuns宏会输出建议备选集的大小:

%mktruns(4 4 4 2 2 2 2),/*一个替代方案的因素水平列表*/

其结果显示如图1。

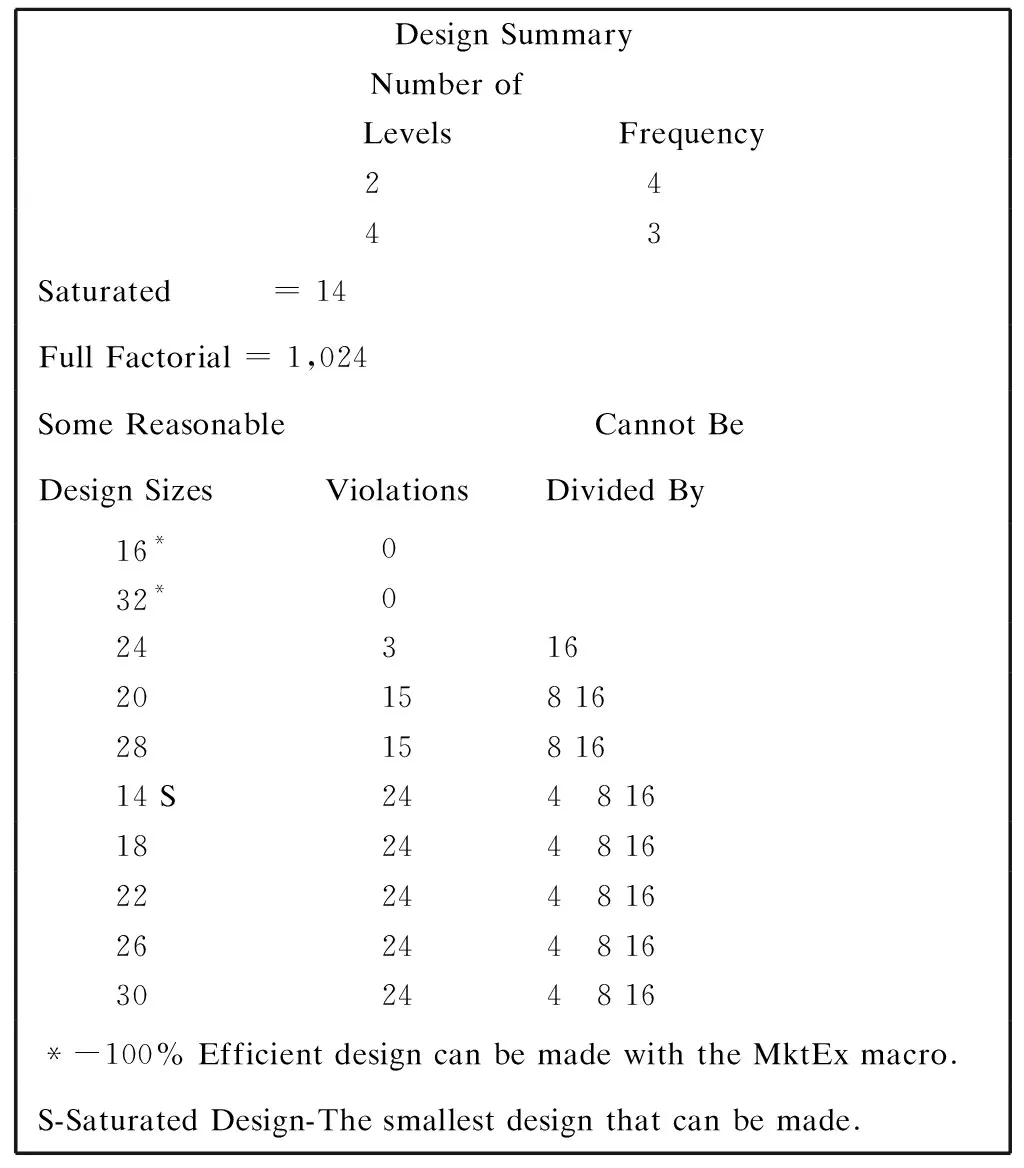
Design SummaryNumber of Levels Frequency2 4 4 3Saturated = 14Full Factorial = 1,024Some Reasonable Cannot BeDesign Sizes Violations Divided By16*032*02431620158 1628158 1614 S244 8 1618244 8 1622244 8 1626244 8 1630244 8 16*-100% Efficient design can be made with the MktEx macro.S-Saturated Design-The smallest design that can be made.

图1%MktRuns宏程序运行结果

结果报告饱和的设计只需要14次运行(一次运行即一个因素水平的组合,也就是一个选项方案),而16次和32次运行是可以产生最优设计的运行次数。我们也可以选择128、256甚至完整的1024次,这样可以给宏程序更大的自由度去找到一个好的设计。

然后,通过%MktEx创建一个备选集合:

%mktex(4 4 4 2 2 2 2,/*一个替代方案的因素水平列表*/

n=1024)/*备选方案的数量*/

接下来,通过%ChoicEff搜索备选集并创建有效的设计。

%choiceff(data=design,

model=class(x1-x7 / sta),/* 用standardized orthogonal contrast coding拟合模型*/

nsets=16,/*选择集的数量*/

maxiter=100,/* 迭代次数 */

seed=145,/* 随机数种子 */

flags=2,/* 每个选择集里有2个备选方案 */

options=relative,/* 显示relative D-efficiency */

beta=zero)/* 假定beta,Ho:b=0 */

model=class(x1-x7 / sta)选项指定了分析时考虑的最常用的模型。这是一个标准正交对比编码下的主效应模型。如果想看到一个在0～100之间的相对D-efficiency,就要使用该编码方式。maxiter=100选项是要求做基于100个随机初始设计的100个设计(该选项的默认值是maxiter=2)。

最终输出的设计来自第28次迭代的结果,相对D-efficiency为73.40。程序运行的部分结果如图2所示。

Final ResultsDesign28Choice Sets16Alternatives2Parameters13Maximum Parame-ters16D-Efficiency11.7439Relative D-Eff73.3993D-Error0.08521/Choice Sets0.0625

图2%ChoicEff宏程序运行部分结果

将变量水平对应具体的意义,则最终的选择集如表2所示。考虑版面原因,仅显示前2个选择集。检验这16个选择集的设计的正交性、水平平衡，结果如表3所示。表3所示,各因素间相关系数都很小,且没有统计学意义。至于水平平衡的性质,月薪等4水平因素的每个水平应占25%,其他2水平因素的每个水平应各占50%,通过简单计数可发现该设计的水平平衡虽然不是完美,但也较平衡(见表4)。

表2 最终的部分选择集(显示前2个)

表3 相关系数矩阵

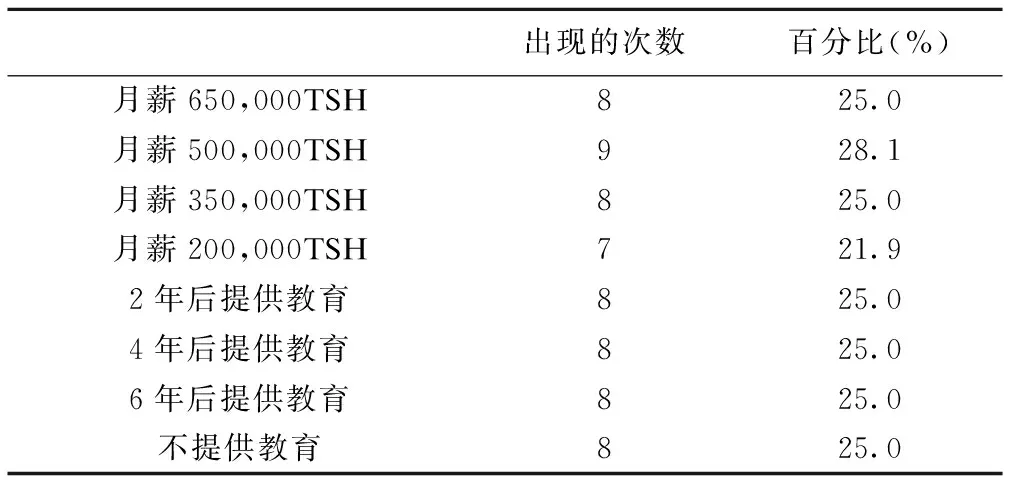
表4 部分因素各水平的频率分布表

讨 论

以往在DCE试验设计中最常用的方法是先通过电脑软件获得一个正交的主效应设计(orthogonal main effect plans,OMEP),然后将产生的方案随机配对成若干选择。而本文介绍了基于SAS 9.4的宏程序进行D-optimal试验。在这个方法中,正交性和水平平衡不是最重要的考量,我们更多地关注设计的功效,通过D评分来衡量。D-efficiency可以分为绝对D-efficiency和相对D-efficiency。具体在设计中采用的编码方式不同会使得绝对的D-efficiency 值发生变化,而相对D-efficiency 是设计与设计间D-efficiency的比值,因此不随编码方式发生变化。大多数软件包中都默认给出相对D-efficiency,这对于大多数研究者来说已经足够了。由于对最佳设计的功效分值没有一个确切的阈值,因此在评价一个设计的好坏时,研究者应该结合相对D-efficiency和其他试验设计的标准[16]。

本文介绍的利用SAS的宏程序实现离散选择试验的设计,只是其中一种方法。其他实现DCE试验设计的方法还包括:人工计算构建试验设计、R语言程序包、Sawtooth软件包、Ngene软件包等可供研究者选择[11,18]。