化归与转化思想在解高考数学题中的应用

李 川

五华县棉洋中学 广东梅州 514459

陕西师范大学数学系罗增儒教授曾说过，如果要用一句话回答“怎样解答高考数学题？”我认为最实用也最重要的是：化归为课本已经解决的问题。众所周知数学高考命题的宏观依据是数学课程标准，数学高考命题的直接依据是数学考试大纲，数学高考命题的最具体、最方便依据是现行数学教材．在近年的全国考试大纲以及各省的考试说明中均说到对数学思想方法的考查，是对数学知识在更高层次上的抽象和概括的考查，考查时必然要与数学知识相结合，通过对数学知识的考查，反映考生对数学思想方法的掌握程度．考查时，应从学科整体意义和思想含义上立意，注重通性通法，淡化特殊技巧。高考主要考查的有七个基本数学思想方法：函数与方程的基本数学思想（通过函数题）、数形结合的基本数学思想（通过函数题，解析几何综合题，构造图形等）、分类与整合的基本数学思想（通过综合题，排列组合题，参数讨论题）、化归与转化的基本数学思想（通过综合题）、特殊与一般的基本数学思想（通过综合题）、有限与无限的基本数学思想（通过极限、微积分函数题）、或然与必然的基本数学思想（通过概率、统计题）。罗增儒教授所说的化归为课本已经解决的问题就体现出化归与转化思想在解决高考题的作用。本文将结合历年的高考题探讨一下化归与转化思想在解高考数学题中的应用。

一、什么是化归与转化的思想

化归与转化的思想是在研究和解决数学问题时采用某种方式，借助某些知识，将问题进行等价转化，使抽象问题具体化，复杂问题简单化、未知问题已知化等，进而达到解决问题的数学思想。这种化归思想在一套高考卷中都是适用的。

二、用化归与转化的思想解高考题实例

1、化归成教材上的题解高考题

题型一：（2006年陕西省理科21题）如图1，三定点A（2，1），B(0，-1)，C(-2,1)；三动点 D，E，M 满足

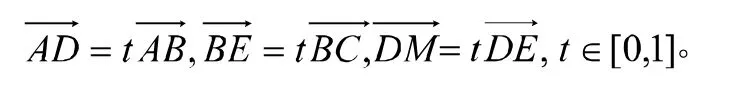
（1）求动直线DE斜率的变化范围；

（2）求动点M的轨迹方程。

评析：该题目对应的教材背景为：

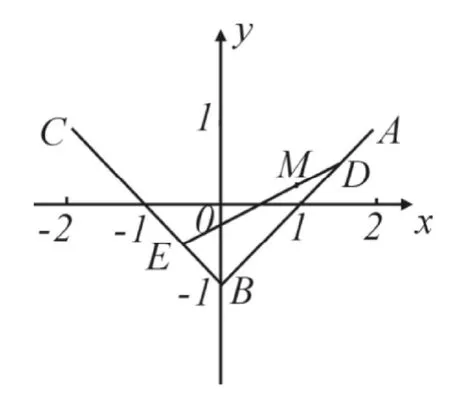
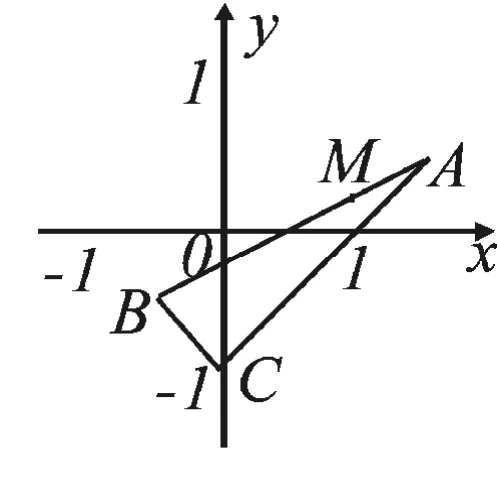
人教版高中《数学》第一册（下）第109页例5为通过该题的背景我们要明白课本是学生知识资源的基本来源，也是学生解题体验的主要引导。课本是高考命题的基本依据。很多高考题目都是直接取自教材，或为原题、或为类题。

其形式可以是课本概念、例题、习题的改编．也可以是教材中的几个题目、几种方法的串联、并联、综合与开拓．甚至少量难题也是按照课本内容设计的，在综合性、灵活性上提出较高要求。

（Ⅰ）求轨迹的方程；

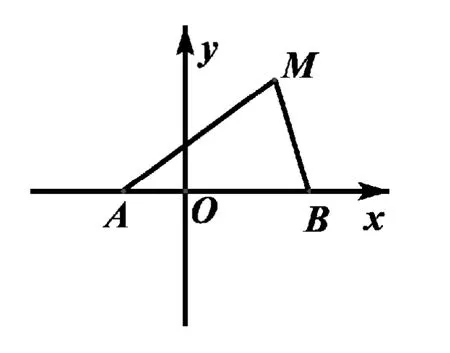
评析：该题完全取之于教材上的原体（1）问没有变化，（2）问有所改变。

2、化归成定义解高考题

评析：本小题考查抛物线的定义、点到直线的距离，属于综合题。而该题的核心就是要让学生明白直线l2：x= 1为抛物线y2=4x的准线，从而将问题化归到抛物线的定义中解题。即化为在抛物线y2=4x上找一个点P使得到点F 1,0和直线l2的距离之和最小，最小值为F 1,0到直线l1:4x3y+6=0的距离，即故选择A。

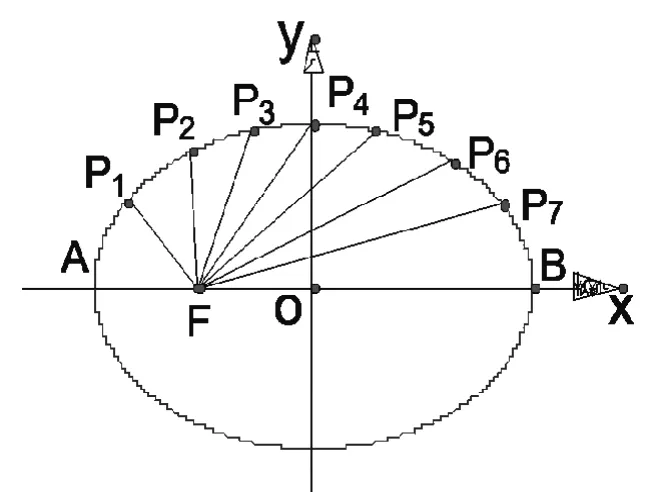
评析：该题是一道典型的用椭圆定义解题的题目，同时又兼顾考查椭圆的对称性。把椭圆的长轴AB分成8等份，过每个分点作x轴的垂线交椭圆的上半部分于七个点，F是椭圆的一个焦 点，则 根 据 椭 圆 的 对 称 性 知，同理其余两对的和也是2a，又

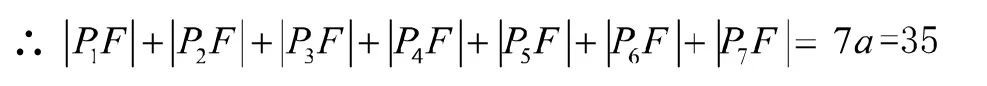
3、化归成基本数学模型处理

题型五：（2009年四川高考17题）在 中，A,B为锐角，角A,B,C所对应的边分别为a,b,c，且求A+B的值；（II）若，求a,b,c，∵的值。 、为锐角，

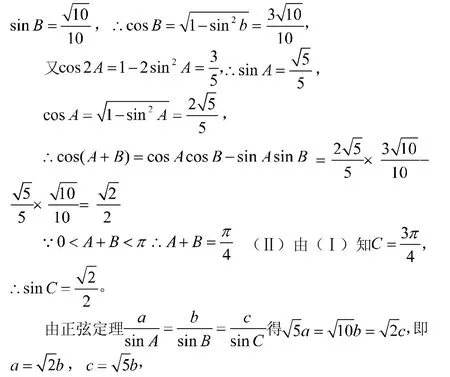
评析：改题是文科选择题压轴题，本题处理方式就是要将其化归成函数这一数学模型处理。利用函数中导数这一解决函数的基本工具处理。