本是同“根”生
2018-12-28张瑜
张 瑜
南京市第十二中学 江苏南京 210011
一、提出问题
我们知道,将两个相交的圆的方程相减,得到两圆公共弦所在直线方程,如果将两个不相交的圆的方程相减,会得到什么呢?它具有什么性质呢?
很明显,这个方程表示的是一条直线l。它有什么性质呢?设点 为直线上的任意一点,由(*)式可得:
即,所以
,可知 。
这说明,将两圆的方程作差可以得到一条直线方程l,过l上的任意一点作两圆的切线,则两切线长相等,这条直线叫做两圆的“根轴”。利用这一结论,我们可以方便地解题。
二、根轴的由来和相关性质
1.根轴的定义和方程
平面几何中有一条著名的定理——圆幂定理:过平面上一定点M,任作一直线与半径为R的定圆O交于A、B两点,则MA MB为定值k(这里MA、MB、表示有向线段的数量),并且 。定值k为点M对圆O的幂,简称“圆幂”。可以证明:对于不同心的两定圆等幂的点的轨迹,是垂直于连心线的一条直线,该直线称为两圆的根轴,也称等幂轴。
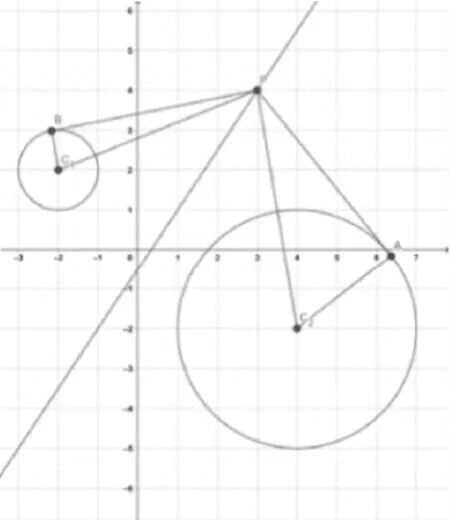
当点在圆内时,点对圆的幂小于零;当点在圆上时,点对圆的幂等于零;当点在圆外时,点对圆的幂大于零(其值等于该点到圆的切线长的平方)。因此,对两圆等幂的点或者同在两圆内,或者同在两圆上,或者同在两圆外(此时该点到两圆的切线长相等)。特别的,当两圆相交时,根轴即两交点的连心线;当两圆相切时,根轴即为过切点的公切线;当两圆外离或内含时,根轴与两圆均不相交。

2.根轴的性质和相关结论
根轴的性质如下:
(1)平面上任意两圆的根轴垂直于它们的连心线;
(2)若两圆相交,则两圆的根轴为公共弦所在的直线;
(3)若两圆相切,则两圆的根轴为它们的内公切线;
(4)蒙日定理(根心定理):平满上任意三个圆心不共线的圆,它们两两的根轴或者相互平行,或者交于一点,这一点叫做它们的根心。
三、根轴的应用
由于根轴有明显的几何意义,其方程又很容易直接构造获得,因此利用它解决问题,很多时候非常方便有效。下面把考试中常考的几个题型利用根轴的性质来解答,拓宽我们的视野。
1.求切线的方程


2.求圆方程问题3.求对称圆的方程

这些经典的题目,换了一种思路来做,开拓了思维,带给我们更多的思考和启发,让教师们的解题思路多维且具有一定的高度。
要给学生一碗水,教师得是自来水。教师虽然面对的知识没有变化,但自己要善于学习,丰富自己的知识,拓宽自己的眼界,做一个研究型的教师。
圆和直线题,有“轴”不要急,本是同“跟”生,构造来解题。
