轴压和扭转复合载荷作用下氮化硼纳米管屈曲行为的分子动力学模拟∗

曾强 张晨利

(上海交通大学工程力学系,上海 200240)

(2018年4月10日收到;2018年9月10日收到修改稿)

采用分子动力学方法模拟了氮化硼纳米管在轴压和扭转复合荷载作用下的屈曲和后屈曲行为.在各加载比例下,给出了初始线性变形阶段和后屈曲阶段原子间相互作用力的变化,确定了屈曲临界荷载关系.通过对屈曲模态的细致研究,从微观变形机理上分析了纳米管对不同外荷载力学响应的差异.研究结果表明,扶手型和锯齿型纳米管均呈现出非线性的屈曲临界荷载关系,复合加载下的屈曲行为具有强烈的尺寸依赖性.温度升高将导致屈曲临界荷载的下降,且温度的影响随加载比例的变化而变化.无论在简单加载或复合加载中,同尺寸的碳纳米管均比氮化硼纳米管具有更强地抵抗屈曲荷载的能力.

1 引 言

将碳纳米管中的碳(C)原子交替替换成氮(N)和硼(B)原子,即可得到氮化硼纳米管(boron nitride nanotubes,BNNTs)[1].1994年,Rubio等[1]通过理论计算预测BNNTs可以稳定存在.1995年,Chopra等[2]通过等离子电弧放电法成功制备出了单壁BNNTs.由于同碳纳米管(carbon nanotubes,CNTs)具有极为相似的结构特征,BNNTs同样表现出优异的力学、物理和化学等特性[3−5],因而引起众多科研工作者的关注.

关于纳米管在不同荷载作用下的力学变形特性和非典型屈曲行为一直是纳米力学领域研究的热点之一[6−15].Liao等[6]借助分子动力学方法(molecular dynamics,MD)模拟给出扶手型BNNTs的拉伸断裂应变约为26.7%.Wang等[7]通过研究发现,在BNNTs中填充铜原子,可以有效提高其抵抗压缩屈曲的能力.纳米结构物的几何尺寸常对其力学行为有显著影响,这是其区别于宏观结构物的一个重要特征.通过对扭转变形的模拟研究,Ajori和Ansari[10]指出,单壁BNNTs的临界扭矩随管长的增大而减小,随管径的增大而增大.Xiong和Tian[11]也发现了类似规律.另一方面,温度升高引起的原子热振动也会对纳米结构物的力学行为产生重要影响.近期的研究表明,温度升高将导致BNNTs在轴压变形中的临界荷载下降13%左右[12,13].

总体来说,目前关于BNNTs力学变形行为的研究主要围绕简单加载的情况展开.实际上,BNNTs无论在制备过程中,还是在具体应用阶段,都不可避免地处于各种简单荷载同时作用的复合受力状态,并可能经历温度的变化[16].因此研究复合荷载作用下BNNTs的力学行为,对于进一步理解其微观变形机理有重要意义.本文采用非平衡态的MD研究BNNTs在轴压和扭转复合荷载作用下的变形屈曲行为,考虑温度变化对屈曲行为的影响,获取临界关系曲线,并与相应CNTs的结果进行比较,力图为深入理解纳米微管在复合荷载作用下的形变机理提供有价值的理论参考依据.

2 模拟方法

本文借助通用的MD模拟软件Lammps[17]实现对BNNTs原子层次的模拟.原子间相互作用势函数的选择是MD模拟的关键所在.基于量子力学键级观念发展起来的Tersof f多体势[18−20]可以考虑B—N共价键的sp2杂化作用,能正确模拟共价键的形成与破坏,已经成功应用于BNNTs变形行为的模拟计算[9−11,14,15,21,22].Tersof f多体势是原子间距离、键角等的函数,在极低温度的模拟计算中也能正确反映BNNTs原子间的相互作用.文献[9,11]用该势分别在0.01和1 K的低温下进行了MD模拟计算.

MD模拟中需要对系统温度进行合理的控制.本文分别在50,300,700和1200 K四种不同温度下进行BNNTs复合加载行为的模拟计算,以探索温度对屈曲行为的影响,因此选取合适的温控机理直接关乎模拟结果的正确性.目前Nose-Hoover温控机理在BNNTs的MD模拟中得到了广泛应用[9−11,15].该机理可以把任何数量的原子与一个热浴耦合起来,消除局域的相关运动,形成一个负反馈机理,已被证明可以产生真实的正则系综[23].本文采用Nose-Hoover温控机理控制模拟系统的温度达到目标温度.

为了探索几何尺寸对力学行为的影响,选取了三组纳米微管进行研究.首先选用一对具有相近几何尺寸而螺旋性不同的微管,扶手型(8,8)-BNNT和锯齿型(14,0)-BNNT,长度约为6.00 nm,半径约为0.56 nm.第二组为具有不同半径的扶手型(6,6),(8,8)和(10,10)-BNNT,长度均为6.00 nm.第三组是长度分别为4.00,6.00和8.01 nm的(8,8)纳米管.每个纳米管两端都被刚化,中部为可以自由运动的调温原子.一端的刚化端被固定,另一端在适当的约束下施加按特定比例增加的轴压和扭转位移,如图1所示.加载开始前首先对纳米管进行结构优化并在确定的温度下自由弛豫,以达到稳定的平衡态.然后采用准静态的加载方式,每次施加微小的复合位移增量,使纳米管充分弛豫达到变形后的稳定态,通过记录MD模拟的结果,获取原子间相互作用力、应变能以及形变量等数值.

图1 (8,8)-BNNT MD模拟计算模型Fig.1.Snapshot of the MD simulation system for(8,8)-BNNT.

3 结果与分析

在复合加载情况下,BNNTs同时发生轴向压缩和扭转变形,因此处于轴向正应力和剪应力同时存在的复合应力状态.定义复合荷载的加载比例为

其中σ和τ分别代表正应力和剪应力.根据弹性理论,无量纲量µ与轴向内力F和扭矩M的关系为

(2)式中R为氮化硼纳米管的半径.改变加载比例,对MD模拟结果进行统计整理,根据B—N键合力计算得出轴向内力F与扭矩M,根据纳米管变形情况计算出轴向应变ε和转角φ.进而可以获得轴向内力F与轴向应变ε的关系,以及扭矩M与单位长度扭转角φ的关系.图2给出了室温300 K下,扶手型(8,8)-BNNT在轴压和扭转复合荷载作用下的屈曲和后屈曲行为,包括4种不同的加载比例µ值,分别为5.59,2.48,0.98和0.48.为进行比较,纯轴压和纯扭转情况下的力学响应也同时给出.可以看出,无论在简单加载或复合加载中,纳米管在初始变形阶段都表现出线性力学行为,内力随着变形量的增加而线性增大.到达临界点时,纳米管的内力达到最大值.观察纯轴压对应的曲线A,轴向内力F在临界点之后出现了突然的下降,之后基本稳定在某一低值附近,随应变的增大没有出现很明显的变化.对于µ值较大的1和2曲线,屈曲和后屈曲行为与纯轴压情况类似.轴向内力在达到最大值(临界点)之后都有明显的下降,之后随应变的增大没有大幅度的增减.曲线2对应的扭转荷载相对较大,引起了内力F略有减小.轴向内力在临界点之后的突降是由于纳米管发生结构失稳,呈现管壁内陷的屈曲模态,引起B—N键合力突然减小造成的.对于扭转荷载占较大比例的曲线3和4,扭矩在临界点之后先是逐渐减小,然后由于扭转屈曲变形加剧再缓慢增大,与纯扭转的情况有一定相似性,而轴力并没有出现非常明显的突降.

图2 (8,8)-BNNT在轴压和扭转复合荷载作用下的屈曲和后屈曲行为(T=300 K) (a)轴力-应变曲线;(b)扭矩-扭转角曲线 (曲线A和B分别代表纯轴压和纯扭转加载情况;曲线1—4代表复合加载情况,1,µ=5.59;2,µ=2.48;3,µ=0.98;4,µ=0.48)Fig.2.Buckling and postbuckling behavior of(8,8)-BNNT under combined axial compression and torsion(T=300 K):(a)Axial force-strain curves;(b)torquetwist angle curves(the notations A and B stand for mechanical loads of pure axial compression and pure torsion,respectively. Curves 1 to 4 correspond to combined loading cases,1,µ=5.59;2,µ =2.48;3,µ=0.98;4,µ=0.48).

图3给出了复合荷载作用下,(8,8)-BNNT的平均应变能随应变的变化曲线,临界点处以小圆点标出.首先,在结构失稳之前,应变能与应变之间基本符合二次关系,这与初始阶段的线性变形行为相对应.到达临界点时,加载比例分别为5.59和2.48的曲线1与2出现了应变能的突降,而曲线3和4的应变能基本无变化.说明对于加载比例较大的曲线1与2情况,纳米管由于结构屈曲而释放了部分应变能,致使应变能突然有所减小.而对于扭转荷载占较大比例的曲线3和4,结构的屈曲模态与纯扭转情况有一定相似性,没有引起应变能的突降.临界点之后,四种加载比例下的应变能基本都随应变线性增加.

图3 (8,8)-BNNT在轴压和扭转复合荷载作用下应变能随应变的变化(T=300 K;曲线1,µ=5.59;曲线2,µ=2.48;曲线3,µ=0.98;曲线4,µ=0.48;临界点用小原点标出)Fig.3.Variation of strain energy as a function of axial strain for(8,8)-BNNT under combined axial compression and torsion(T=300 K;curve 1,µ=5.59;curve 2,µ =2.48;curve 3,µ =0.98;curve 4,µ =0.48;the critical points are marked by solids dot).

借助MD模拟,可以观察不同荷载作用下屈曲的产生细节和发展过程,对于理解BNNTs复杂的微观变形机理有重要意义.在轴压屈曲中,管壁处于轴向压应力状态,当压应力增大到一定数值,管壁会发生突然的局部内陷而诱发屈曲,纳米管呈现出扁平屈曲面.在扭转变形中,管壁中拉应力区域和压应力区域各呈螺旋分布,即同一横截面既有受拉区,又有受压区.失稳发生时,受压区原子向内侧移动,而受拉区原子向外凸出,横截面由圆形变成椭圆形,扭转失稳是逐渐发生的,并没有突然的局部管壁内陷.在轴压和扭转复合荷载作用下,管壁中应力状态比较复杂,既有拉应力,也有压应力.随加载比例不同,拉、压应力占的比例也不同.当外荷载增大到一定数值,结构失稳由压应力区管壁的内陷而诱发,同时拉应力区原子向外凸出,结构出现屈曲面,由于扭转荷载作用,屈曲面略呈扭曲.随着变形加深,结构将呈现出典型的屈曲模态.

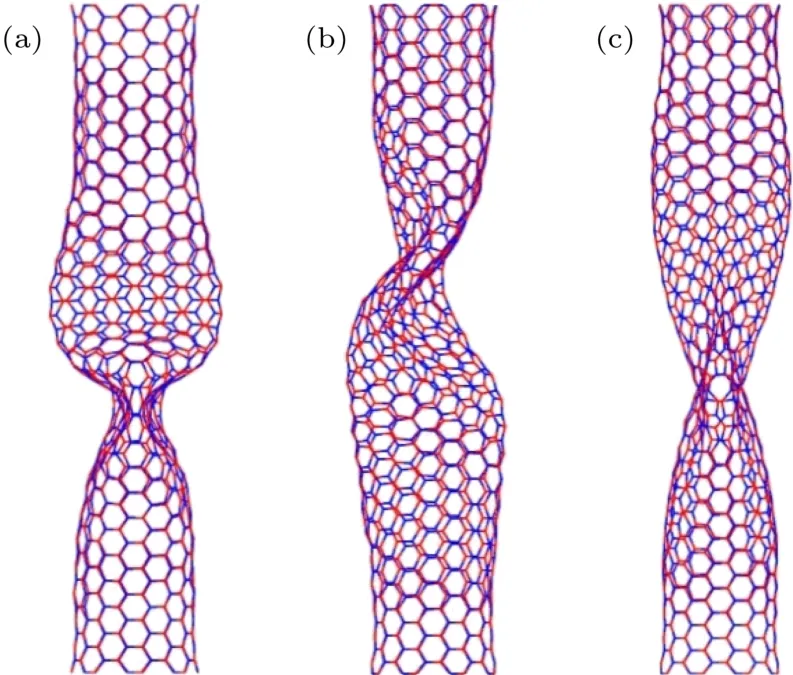
图4(8,8)-BNNT的屈曲模态(T=300 K)(a)纯轴压状态,ε=0.086;(b)复合加载状态,µ=2.48,ε=0.070,φ =10.84(◦)/nm;(c)纯扭转状态,ϕ =11.70(◦)/nmFig.4.Buckling modes of(8,8)-BNNT(T=300 K):(a)Pure axial compression,ε=0.086;(b)combined axial compression and torsion,µ=2.48,ε=0.070,φ =10.84(◦)/nm;(c)pure torsion,φ =11.70(◦)/nm.

图4 给出了扶手型(8,8)-BNNT在三种不同加载情况下的典型屈曲模态.图4(a)和图4(c)分别对应纯轴压和纯扭转情况,图4(b)对应µ值为2.48的复合加载情况.观察图4(b),屈曲模态兼具图4(a)和图4(c)的特征.一方面,BNNT由于管壁内陷形成两个屈曲面,与图4(a)中的两个扁平的屈曲面类似;另一方面,图4(b)中的两个屈曲面并不像图4(a)那样相互垂直,而是沿轴向扭转成斜交,这又与图4(c)中的屈曲模态有一定类似性.图4(c)中,纳米管管壁变形为扭曲的屈曲面.轴压屈曲或类似轴压屈曲中的管壁内陷会引起BNNTs应变能突然释放,同时B—N键合力也随之减小,引起轴向内力突降[9].纯扭转屈曲中基本没有突发的管壁内陷,应变能和B—N键合力也不会发生急剧地变化.BNNTs在不同的荷载作用下,会表现出不同的变形过程和屈曲模态,这是引起原子间相互作用力及应变能变化趋势不同的主要原因.

图5反映了温度变化对复合加载下锯齿形(14,0)-BNNT屈曲和后屈曲行为的影响,对应加载比例值为2.48,模拟温度分别为50,300,700和1200 K.很明显,屈曲临界荷载随着温度的升高而降低,Ali等[12]也通过MD模拟计算得出了类似的结论.这主要是由于高温下原子剧烈地热振动致使管壁上出现许多小的点缺陷,显著降低了纳米管抵抗屈曲的能力.当温度从300 K升高到1200 K时,锯齿形(14,0)-BNNT的临界轴力下降了19%,临界扭矩下降量为13%.通过计算两种简单加载情况,得到纯轴压下屈曲荷载的相应减小量为29%,纯扭转下的相应减小量仅为5%.因此模拟结果表明,温度变化对BNNTs临界轴力影响较大,而对临界扭矩影响较小.高温下原子剧烈地热振动会造成原子间距和键角发生变化,引起原子间相互作用势增大,原子间相互作用力也随之增大,形成局部应力集中.这种应力集中易诱发局部管壁凹陷,而轴压失稳始于局部管壁凹陷,所以高温下轴向屈曲荷载值下降明显.对于扭转变形,屈曲发生不是由管壁凹陷诱发,但局部应力集中也会促使屈曲面的形成,所以温度对扭转屈曲的影响不如对轴压屈曲影响大.

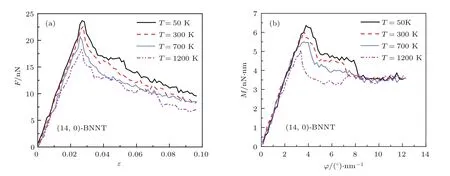
图5 轴压和扭转复合荷载作用下温度对(14,0)-BNNT屈曲和后屈曲行为的影响(µ=2.48) (a)轴力-应变曲线;(b)扭矩-扭转角曲线Fig.5.Effect of temperature change on buckling and postbuckling behavior of(14,0)-BNNT under combined axial compression and torsion(µ=2.48):(a)Axial force-strain curves;(b)torque-twist angle curves.

分析结构在组合荷载作用下的屈曲行为时,一个重要的问题是确定屈曲临界荷载关系.为了探索这一问题,定义两个无量纲参数,

其中和分别为300 K下BNNTs分别在纯轴压和纯扭转下的临界正应力和剪应力,σcr和τcr为纳米管在复合荷载作用下的临界屈曲应力.注意到应力的计算要用到纳米管等效壁厚值,而(3)式中两个参数是应力的比值,所以与壁厚值无关.(8,8)和(14,0)-BNNTs在50,300,700和1200 K四种不同温度下的临界荷载关系曲线如图6所示.对于本文给出的各临界荷载关系曲线,仅图6(b)中和采用的是(14,0)-BNNT在300 K下的临界荷载值,其余曲线均采用(8,8)-BNNT在300 K下的临界荷载值.观察图6,对于两种螺旋性的纳米管,温度效应都随加载比例的增大而增大.即轴压荷载相对越大,温度对屈曲行为的影响越显著.对比两种螺旋性的BNNTs,扶手型纳米管的关系曲线在加载比例较大时表现为非线性,当RS>0.6时,曲线近似呈现线性关系.锯齿型(14,0)-BNNT的曲线仅在RS>0.85时呈现线性关系,其余均为非线性.说明纳米管的螺旋性对临界荷载关系曲线的形状略有影响.

图7(a)给出了三个不同半径扶手型(6,6),(8,8)和(10,10)-BNNT的临界荷载关系曲线,纳米管长度均为6.00 nm;图7(b)比较了不同长度(8,8)-BNNT的临界荷载关系.可以看出,在复合加载的情况下,BNNTs的力学行为也表现出强烈的尺寸效应.在长度相同的情况下,临界正应力和剪应力都随半径的增大而减小.对同一种纳米管,两种临界应力都随长度的增大而减小,且扭转荷载相对越大,长度的影响越显著.这与已有文献报道中给出的变化规律一致[10−12].尺寸效应是纳米结构物区别与宏观物体的重要特性之一,借助MD的大量模拟结果,可以获取BNNTs的力学行为随其尺寸变化的一般规律.

图6 轴压和扭转复合荷载作用下温度对BNNTs屈曲临界荷载关系的影响 (a)(8,8)-BNNT;(b)(14,0)-BNNTFig.6.Effect of temperature change on the interactive buckling loads curves of BNNTs under combined axial compression and torsion:(a)(8,8)-BNNT;(b)(14,0)-BNNT.

图7 轴压和扭转复合荷载作用下尺寸对BNNTs屈曲临界荷载关系的影响(T=300 K) (a)纳米管半径的影响;(b)纳米管长度的影响Fig.7.Effect of nanotube size on the interactive buckling loads curves of BNNTs under combined axial compression and torsion(T=300 K):(a)Effect of nanotube radius;(b)effect of nanotube lengths.

众所周知,BNNTs和CNTs具有非常相似的原子连接结构,将CNTs中的碳(C)原子交替替换成氮(N)和硼(B)原子,即可得到BNNTs.目前已经开展了关于CNTs和BNNTs杂化或嵌套结构的研究[15,22,24,25].杂化或嵌套结构可以使两种管优势互补,发挥各自的长处.因此有必要对两种管的力学性能进行充分对比分析[21],以指导杂化或嵌套结构的优化设计,得到性能更加出色的纳米微管.

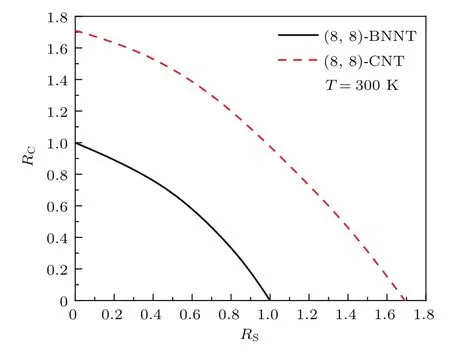
图8 轴压和扭转复合荷载作用下BNNTs和CNTs屈曲临界荷载关系曲线的比较(T=300 K)Fig.8.Comparisons of the interactive buckling loads curves between BNNTs and CNTs under combined axial compression and torsion(T=300 K).

图8 比较了室温300 K时,在轴压和扭转复合荷载作用下,同尺寸、同螺旋性的单壁BNNTs和CNTs的临界荷载关系曲线.可以看出,无论在轴压、扭转还是复合加载条件下,CNTs均比BNNTs具有更强地抵抗屈曲荷载的能力,这种差异可能是由于两种管中原子不同的键合方式引起的.BNNTs中的B—N键具有离子键的特性,而碳纳米管中的C—C键为共价键,C—C键较B—N键表现出更强的键合力.另一方面,两条曲线特征具有一定形似性,反映出两种纳米管在不同荷载作用下的力学响应相似,它们抵抗屈曲能力的差异不随加载比例的变化而变化,因此两种管的杂化或嵌套结构可以协同工作,发挥更加优异的力学性能.Xiong和Tian[11]借助MD方法,得出同尺寸CNTs的临界扭矩高于BNNTs.Wei等[9]也发现,低温下同螺旋性的CNTs比BNNTs具有更高的临界轴向屈曲应力,与本文的研究结论一致.

此外,BNNTs具有良好的热稳定性.实验表明,BNNTs可以耐受1200—1400 K的高温,而CNTs在400◦C即发生氧化,在700◦C左右即可能燃烧[26].因此当环境温度较高时,两种管的杂化或嵌套结构可以充分发挥各自的优势,取长补短,形成性能更加优异的纳米微管结构,从而具有更加广泛的应用前景,这也是目前纳米力学中方兴未艾的研究课题之一.

4 结 论

本文研究了轴压和扭转荷载共同作用时,几何尺寸和环境温度对BNNTs变形和屈曲行为的影响.借助MD获取了纳米管原子间相互作用力及应变能随形变的变化规律、典型的屈曲模态以及屈曲临界荷载关系.并将BNNTs和CNTs的模拟结果加以比较,以探索两种纳米管力学行为的差异.分析研究表明,加载形式不同,BNNTs表现出不同的变形屈曲模态,从而引起原子间相互作用力的变化趋势也不相同.温度升高将导致屈曲荷载和后屈曲平衡路径的下降,且加载比例越大,温度效应越明显.复合加载情况下的临界应力随长度和半径的增大而减小.两种螺旋性的BNNTs均基本呈现出非线性的屈曲临界荷载关系.无论在轴压、扭转还是复合加载条件下,同尺寸的CNTs均比BNNTs具有更强地抵抗屈曲荷载的能力.可以预测,BNNTs与CNTs的杂化或嵌套结构将拥有更加优异的力学性能,应用前景更加广泛.