基础水平运动的弹簧摆的周期解与稳定性∗

张利娟 张华彪 李欣业

1)(河北工业大学机械工程学院,天津 300130)

2)(天津商业大学机械工程学院,天津 300134)

(2018年9月8日收到;2018年10月22日收到修改稿)

针对基础水平运动的弹簧摆的非线性动力学响应进行研究,利用拉格朗日方程建立了系统的动力学方程.将离散傅里叶变换、谐波平衡法以及同伦延拓方法相结合,对系统的周期响应进行求解,避免了传统方法计算中使用泰勒展开引起的小振幅的限制,与数值计算结果的对比表明该求解方法具有较高的精确度.利用Floquet理论分析了周期响应的稳定性,给出了基础运动振幅和频率对系统周期响应的影响.研究发现:对应某些基础频率和振幅,系统的周期响应可能发生Hopf分岔;利用数值计算研究了Hopf分岔后系统响应随基础频率和振幅的变化,发现系统出现了倍周期运动、拟周期运动和混沌等复杂的动力学行为.研究表明系统进入混沌的主要路径是拟周期环面破裂和阵发性.

1 引 言

弹簧摆作为一个典型的两自由度非线性系统,在许多关于非线性振动的专著中都有所论述[1,2],它既可以看成是单摆的推广,也可以看成是单自由度弹簧质量系统的推广.由于人们对这两类单自由度系统非常熟悉,所以弹簧摆特别适合于说明非线性振动系统中的内共振以及其他动力学现象.事实上,在研究大型起重船或吊车作业时悬吊物的摆振问题时就可以将此简化为弹簧摆模型,因此其非线性动力学问题一直得到研究者的关注.

Eissa等[3]用多尺度法研究了六次非线性模型弹簧摆在两个模态都受到简谐激励时主共振、亚谐共振、超谐共振、组合共振响应的四阶近似解,发现参数的变化会导致频响曲线的侧弯.Alasty和Shabani[4]研究了1:2内共振弹簧摆沿呼吸和摆动模态都受简谐激励时主共振响应的混沌运动,发现除了奇怪吸引子外还有多个共存的规则吸引子,且后者的吸引域边界是分形的.Starosta等[5]研究了内共振弹簧摆受不同频率简谐激励时的参数激励共振-主共振响应,结果表明频响曲线既可以呈硬特性也可能呈软特性.Awrejcewicz等[6]对摆锤沿摆动的径向及切向分别受简谐激励的弹簧摆,利用多尺度法研究了弹簧的非线性和耦合强度对稳态和瞬态共振响应的影响,得到了稳态共振响应的频响特性方程以及非稳态响应的近似渐近解.Klimenko等[7]研究了弹簧摆和一个单摆吸振器系统的动力学响应,计算了系统的非线性模态,并通过稳定性分析给出了不同非线性模态的稳定和不稳定区域.萧寒等[8]基于多尺度法研究了在单频激励下1:2内共振平方非线性模型弹簧摆主共振响应鞍结分岔的控制问题,设计的反馈控制器不仅能使系统的振幅得到有效的控制,还可以将弹簧摆的扰动控制到一条稳定的周期运动轨道上.全局响应方面,Sousa等[9]提出了一种用于研究非线性耦合系统能量交换方式以及系统参数对能量交换影响的方法,并将其应用于弹簧摆系统,分析了系统的摆动和呼吸运动之间的能量转换,给出了弹簧摆系统能量分布的全局特征.Lee[10]利用插值映射法研究了平方非线性模型弹簧摆存在1:2内共振关系时在简谐激励下主共振稳定周期响应的全局吸引域问题,发现在四维状态空间中存在一个特殊的平面,包含了全部吸引子.Lee和Park[11,12]利用多尺度法分别研究了同时含有平方和立方非线性并具有1:2内共振关系的弹簧摆在简谐激励下主共振响应的一阶和二阶近似解的混沌运动,分岔图和李雅普诺夫指数结果表明,二阶近似解比一阶近似解能更好地与原系统吻合.Zaki等[13]利用数值方法讨论了只沿切线方向受简谐激励的弹簧摆非主共振响应的分岔和通向混沌的道路,发现弹簧的非线性对其有重要的影响.Tian等[14,15]研究了具有无理式和分式形式非线性恢复力的弹簧摆,利用多尺度法分析了泰勒展开后的系统的周期响应,利用改进的Melnikov方法给出了系统出现混沌的阈值,并进行了数值验证.Awrejcewicz等[16]研究了同时有两个方向外激励的弹簧摆的非稳态响应,利用多尺度法给出了系统非稳态响应的包络线和极限相轨迹.Digilov等[17]建立了弹簧摆上变质量阻尼振荡模型,该模型的质量以恒定速率衰减,讨论了质量损失率对阻尼参数大小的影响.Eissa等[18]将横向调谐吸振器应用于多参数激振的弹簧摆系统的振动控制中,研究了次谐共振和内共振情况下的周期解及其稳定性,讨论了吸振器和系统参数对响应的影响.

除了简谐激励外,受基础激励的弹簧摆也是研究的热点之一.Gitterman[19]对悬挂点做竖直方向简谐运动和受到外加激励的弹簧摆进行了比较研究,为此将运动微分方程中的三角函数做泰勒展开后截取到四次项,用多尺度法求取了四阶近似解.结果表明,当外激励和黏性阻尼为同阶小时,二者的低阶近似解是一样的,但当阻尼力比外激励更小时,低阶近似解是不同的.Amer等[20,21]分别对沿圆形轨迹和椭圆轨迹移动的弹簧摆进行研究,采用多尺度法求得了系统的周期解,并进行了稳定性分析,同时利用数值计算分析了周期解失稳后的响应.他们又将摆球由质点改为刚体开展研究[22],对系统的共振情况进行分类,给出了稳态解的可解条件.

工程中很多弹簧摆系统在工作时其基础是水平运动的,可能是在平衡位置附近的左右往复运动,也可能是行进过程中的变速运动,然而针对基础水平运动弹簧摆的研究并不多见.同时对于已有的弹簧摆甚至单摆的研究,特别是周期解的计算中,由于动力学方程中存在摆角的三角函数项,传统解析方法无法处理,只能对摆角进行泰勒展开后再进行研究.众所周知,泰勒展开只在展开点附近是相对精确的,因此泰勒展开后的动力学方程只适用于摆动角度很小的情况,而在摆动角度很大时,其所得的分析结果往往是不准确,甚至错误的.特别是对于基础激励的情况,其动力学方程中除回复力外,在激励项中也含有摆角的三角函数,泰勒展开不仅改变了回复力的大小,还改变了激励的形式.因此针对未经泰勒展开的弹簧摆系统的动力学方程开展研究,特别是研究大摆角情况下的周期解及其稳定性具有更高的理论价值.

基于上述问题,本文针对基础水平运动的弹簧摆的响应开展研究.第2部分利用拉格朗日方程建立了基础水平运动的弹簧摆的动力学方程;第3部分将谐波平衡法、离散傅里叶变换以及同伦延拓方法相结合,直接对未经泰勒展开弹簧摆系统的动力学方程进行求解,求得了系统的周期响应;第4部分针对系统周期解的稳定性进行研究;第5部分分析了基础频率和振幅对系统响应的影响;最后对本文的主要结论进行总结.

2 基础水平运动弹簧摆的动力学模型

图1 基础水平运动的弹簧摆Fig.1.Spring pendulum with base motion in the horizontal direction.

图1 为基础水平运动的弹簧摆模型,其中x1为摆球沿弹簧长度方向的位移,x2为弹簧摆的角位移,m和k分别表示摆球的质量和弹簧的刚度,l为摆长,有l=l0+mg/k,其中l0为弹簧的原长.我们定义o为坐标系原点,建立如图1所示x-o-y坐标系,则摆球的位置可表示为

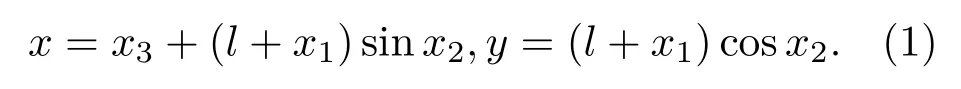
因此摆球的速度可写作:

图2 弹簧摆响应的相图和频谱 (a)Ab=0.3 m,ω=4 rad/s,初值(1.09,1.43,1.26,0.11),仿真时间τ=0—800π;(b)Ab=0.3 m,ω=2.22 rad/s,初值(0.25,0.93,−0.33,0.98),仿真时间τ=0—800πFig.2.Phase diagram and spectrum of spring pendulum:(a)Ab=0.3 m,ω=4 rad/s,initial value(1.09,1.43,1.26,0.11),simulation time τ =0–800π;(b)Ab=0.3 m,ω =2.22 rad/s,initial value(0.25,0.93,−0.33,0.98),simulation time τ =0–800π.

摆球的动能、势能、瑞利耗散函数分别为利用拉格朗日方程可得系统的运动方程,有

本文主要考虑基础做简谐运动的情况,因此有x3=Abcosωt.定义X1=x1/l,X2=x2,τ=ωt,对方程进行无量纲化并化简,有

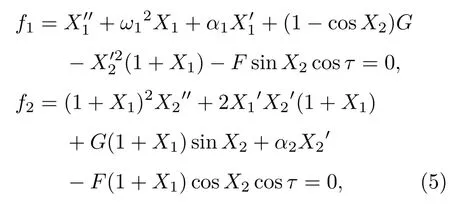
其中

对方程(5)进行数值求解,如无特殊说明,本文设定计算参数为m=0.5 kg,k=20 N/m,l=1 m,g=10 m/s2,c1=0.1 Ns/m,c2=0.1 Ns.

图2给出了弹簧摆运动的相图和频谱,可以看到系统周期响应的频率成分非常复杂,采用传统方法求1次或者几次谐波解无法准确地描述周期解的响应特性,因此本文将谐波平衡法和同伦延拓方法相结合对系统进行高次谐波求解.

3 基础水平运动的弹簧摆的周期解

设方程的解为

其中A和B分别为各次谐波的系数,n为所求解的最高次谐波数.将(7)式代入方程(5),利用傅里叶变换提取各次谐波系数,可得关于振幅的代数方程如下:

下面将利用同伦延拓方法对(8)式进行求解,为了便于说明求解过程,令z=[z1,z2,···,zh],其中h=4n+3,z1=A0,z2=B0,z4i−1=A1i,z4i=A2i,z4i+2=B2i,z4i+1=B1i,zh为所要研究的系统参数,则方程(8)可写作

其中,H(z)=[H1,H2,···,Hh−1]T. 设定zj(zj∈Rh)为解曲线上的一个正则点(z0可以通过给定系统参数,利用牛顿拉普森法求得),沿该点的切线方向预估,下一个预测点可写作

式中δj为第j部的步长;uj为预测方向,满足下列要求

从p=1开始迭代,直到满足∥yp+1−yp∥6ε时停止,下一个点zj+1=yp+1.

理论上利用上述方法可以求得系统参数对各次谐波振幅的影响.但实际计算中,H(yp)和H′(y0)的计算需要对(8)式中的积分进行直接解析求解,考虑到f1,f2中含有X2的三角函数项,这是非常困难的,特别是当谐波数较多,即n较大时,解析求解几乎是不可能的.因此我们采用数值方法求取H(yp)和H′(y0),将τ在一个周期2π内等分成q份,则τ变为一个等差序列[0,2π/q,4π/q,6π/q,···,2(q−1)π/q],给定yp的值,代入到(7)式中,则X1,X2都变成了时间序列,然后将X1,X2代入方程(5),则f1,f2变为(h−1)×q的序列,对该序列进行离散傅里叶变换可以求得H(yp)的值.对于导数矩阵H′(y0),有

矩阵中各项可以通过差分形式求得,有

利用上述方法对方程进行求解时,理论上n取值越大,所得解的精度越高,然而n取值过大,则会影响计算效率.我们对系统的周期解进行了大量的数值计算,发现系统的周期解的主要频率成分在20次以内,因此本文设解的谐波次数n=20.图3给出了基础激励的弹簧摆系统的计算结果,其中实线为20次谐波解,圆点为龙格-库塔方法的计算结果,可以看到两者吻合得非常好,特别是图3(b)中摆动方向的振幅已经达到了1.5(角度值约85.9◦),远远超出了微幅振动的范围,因此本文的方法不仅具有较高的求解精度,而且适合于弹簧摆大幅振动的情况.

图3 20次谐波解和数值解的对比(HB,谐波平衡法的结果;RK,龙格-库塔法结果) (a)ω=4 rad/s,Ab=0.3 m;(b)ω=2.22 rad/s,Ab=0.3 mFig.3.Comparison of 20th harmonic solution and numerical solution(HB,the solution of harmonic balance method;RK,the solution given by Runge-Kutta method):(a)ω=4 rad/s,Ab=0.3 m;(b)ω=2.22 rad/s,Ab=0.3 m.

4 周期解的稳定性分析

下面利用Floquet理论研究周期解的稳定性,将方程(5)写作状态方程形式:

其中M=DF().显然M为时变参数矩阵,利用Hsu方法求解,以单位阵为初值,在一个周期内进行数值积分,可求得Floquet乘数矩阵,其特征值为Floquet乘子.当Floquet乘子从1处穿出单位圆时,系统发生静态分岔,Floquet乘子从−1处穿出单位圆时,系统发生倍周期分岔,Floquet乘子从其他位置穿出单位圆时,系统发生Hopf分岔.

5 基础运动频率和振幅的影响分析

图4 基础运动频率对系统振幅的影响(SP,静态分岔点;HP,Hopf分岔点)(a)Ab=0.02 m;(b)Ab=0.05 m;(c)Ab=0.25 m;(d)Ab=0.3 m;(e)Ab=0.4 m;(f)Ab=0.6 mFig.4.Influence of base frequency on the amplitude of system(SP,the static bifurcation point;HP,the Hopf bifurcation point):(a)Ab=0.02 m;(b)Ab=0.05 m;(c)Ab=0.25 m;(d)Ab=0.3 m;(e)Ab=0.4 m;(f)Ab=0.6 m.

图4 给出了对应不同基础幅值时基础运动频率对系统振幅的影响曲线,这里的振幅是20次谐波叠加后振动位移的最大值,表1是对应图4中各分岔点的分岔形式和Floquet乘子的变化,可以看到随着基础频率的变化,系统的振幅出现了两个峰值,当基础幅值Ab=0.02 m时,系统的响应在整个频率范围内都是稳定的周期解.随着基础幅值的增大,响应的两个峰值分别向两个方向发生偏斜,两者之间的距离越来越远,同时系统出现了不稳定周期解.图4(b)—(f)的变化趋势是一致的,随频率的变化先发生两次静态分岔,基础频率在两静态分岔点之间时系统具有两个稳定的周期解,即系统具有双稳态现象.然后随着基础频率的增大,系统将发生两次Hopf分岔.而当ω>3.5 rad/s时,图4(b)的下一个静态分岔点出现在转折点处,而图4(c)—(f)中下一个静态分岔点出现在曲线的中段.图4(c)和图4(d)在ω=5 rad/s附近有稳定的周期解,然后在ω=6 rad/s附近通过静态分岔失稳,而图4(e)中当ω>4.8 rad/s,系统不存在稳定的周期解,图4(f)中系统在ω=5 rad/s附近没有稳定的周期解,然而在ω=6 rad/s附近又出现了稳定的周期解.利用数值计算对图4(c)—(f)中通过静态分岔点P1后的动力学行为进行研究,发现图4(c)中通过P1后系统的响应发生跳跃,跳到下方的周期解轨道上,而图4(d)—(f)通过P1后系统的响应不再是周期运动,稳定的运动中摆动方向的位移随着时间变化持续增大,如图5所示.此时弹簧摆的运动表现为一种旋转运动,称之为旋转解,同时还可以看到此时呼吸运动的最大无量纲振幅超过了1010,由此可知旋转解出现后弹簧摆必然会被破坏,这是工程中必须要避免的.数值计算发现在图4(d)和图4(f)中周期解通过P2点后也会变成旋转解.

表1 对应图4的分岔类型和Floquet乘子的变化Table 1.Bifurcation type and change of Floquet multiplier corresponding to Fig.4.

图5 旋转解的时间历程(Ab=0.3 m,ω=4.81 rad/s;初值(1.133,1.503,1.273,0.113);(c),(d),(e)为(a)的局部放大;(f),(g),(h)为(b)的局部放大)Fig.5.Time process of the rotational solution(Ab=0.3 m,ω=4.81 rad/s;initial value(1.133,1.503,1.273,0.113);panels(c),(d),(e)are the partial enlargement of panel(a),and panels(f),(g),(h)are the partial enlargement of panel(b)).

图6 弹簧摆响应随基础运动频率变化的分岔图和李雅普诺夫指数(Ab=0.3 m;ω=2.8 rad/s时的初值为(−0.27,0.34,−0.63,0.50);仿真时间τ=0—800π) (a)分岔图;(b)李雅普诺夫指数;(c),(d),(e),(f)分岔图(a)的局部放大Fig.6.Bifurcation diagram and Lyapunov exponent of spring pendulum with the change of base frequency(Ab=0.3 m):(a)Bifurcation diagram;(b)Lyapunov exponent;(c),(d),(e),(f)enlargement of the bifurcation diagram(a).The initial value is(−0.27,0.34,−0.63,0.50)when ω =2.8 rad/s.Simulation time is τ=0–800π.

图7 弹簧摆随基础运动频率变化的典型动力学响应的庞加莱映射 (a)周期1运动,ω=2.91 rad/s;(b)拟周期运动,ω=2.92rad/s;(c)拟周期运动,ω=2.93 rad/s;(d)混沌运动,ω=2.9325 rad/s;(e)周期9运动,ω=2.9346 rad/s;(f)混沌运动,ω=2.9348 rad/s;(g)周期6运动,ω=2.9632 rad/s;(h)混沌运动,ω=2.9646 rad/s;(i)拟周期运动,ω=2.992 rad/s;(j)混沌运动,ω=3.002 rad/s;(k)周期7运动,ω=3.17 rad/s;(l)混沌运动,ω=3.172 rad/s;(m)周期27运动,ω=3.1806 rad/s;(n)拟周期运动,ω=3.182 rad/s;(o)拟周期运动,ω=3.48 rad/sFig.7.Poincare map of typical dynamic behavior of spring pendulum with the change of base frequency:(a)Period 1 motion,ω=2.91 rad/s;(b)almost periodic motion,ω=2.92rad/s;(c)almost periodic motion,ω=2.93 rad/s;(d)chaos,ω=2.9325 rad/s;(e)period 9 motion,ω=2.9346 rad/s;(f)chaos,ω=2.9348 rad/s;(g)period 6 motion,ω=2.9632 rad/s;(h)chaos,ω=2.9646 rad/s;(i)almost periodic motion,ω=2.992 rad/s;(j)chaos,ω=3.002 rad/s;(k)period 7 motion,ω=3.17 rad/s;(l)chaos,ω=3.172 rad/s;(m)period 27 motion,ω=3.1806 rad/s;(n)almost periodic motion,ω =3.182 rad/s;(o)almost periodic motion,ω =3.48 rad/s.

对两个Hopf分岔点之间的动力学行为进行数值计算,图6给出了系统响应随基础运动频率变化的分岔图和李雅普诺夫指数,图7给出了系统出现的典型动力学响应的庞加莱映射,可以看到系统在基础运动频率ω=2.91 rad/s时,响应为周期1运动,随着频率的增大,周期1运动发生Hopf分岔变为拟周期运动(见图7(b)),频率继续增大后,拟周期运动发生环面倍化(见图7c)),进而拟周期环面破裂,系统的响应进入混沌(见图7(d)).随后系统的响应在ω=2.933 rad/s附近退出混沌,变为周期9运动(见图7(e)),然后在ω=2.935 rad/s附近通过阵发性再次进入混沌.在ω=2.963 rad/s附近,系统退出混沌,响应为周期6运动,在ω=2.964 rad/s附近重新进入混沌,此时系统的响应在相平面上表现为6个小的吸引子,随着频率的增大,6个小的吸引子很快变成了一个大的吸引子.在ω=2.972 rad/s附近系统再次退出混沌,变为周期9运动,在ω=2.984—2.994 rad/s时系统响应为拟周期运动,其庞加莱映射为9个不变环,在ω=3.002 rad/s附近周期9运动通过阵发性回到混沌.在ω=3.168—3.215 rad/s之间,系统响应在周期运动、混沌和拟周期运动之间发生多次切换,典型的响应包括周期7运动、周期27运动、27不变环的拟周期运动和混沌(见图7).然后系统在ω=3.4715 rad/s附近响应变为环面倍化的拟周期运动(见图7(o)),进而回到一个不变环的拟周期运动,随着转速的增大重新转化为周期1运动.需要注意的是,图7(b)、图7(c)、图7(i)、图7(n)和图7(o)都是拟周期运动,然而其运动的本质是不同的,图7(b)的拟周期运动中含有激励的无量纲频率1和Hopf分岔产生的不可约的频率成分ωH及其线性组合,在图7(c)中系统响应发生了环面倍化,其实质是ωH频率成分发生了倍周期分岔,即响应中出现了含ωH/2频率的成分,图7(o)的响应形式和图7(c)类似.而图7(i)和图7(n)的响应实质是由倍周期运动通过Hopf分岔产生的拟周期运动,其频率成分为1/N与Hopf分岔的频率成分ωH及其线性组合,其中N是倍周期运动的周期数.

我们同样研究了基础振幅对响应的影响,图8给出了对应不同基础运动频率时,基础振幅对弹簧摆振幅的影响曲线,表2是与之对应的各分岔点的分岔形式和Floquet乘子的变化.可以看到对应于ω=2.3 rad/s和ω=4.6 rad/s两种情况,曲线都出现了两个静态分岔点,当基础振幅取某些值时,系统出现了两个稳定解和一个不稳定解,随着基础振幅的变化,响应的振幅将发生跳跃现象;而在ω=6 rad/s时,系统在Ab=0.2 m附近的静态分岔点失稳后将进入旋转状态,在Ab=0.53—0.6 m之间稳定周期解和旋转解共存,系统的响应将取决于初始状态;在ω=2.9 rad/s时,当基础振幅较小时,系统响应随基础振幅的变化将发生跳跃,而在Ab=0.328 m附近系统将发生Hopf分岔,响应由周期运动变为拟周期运动.

图8 基础振幅对系统响应振幅的影响(SP,静态分岔点;HP,Hopf分岔点) (a)ω=2.3 rad/s;(b)ω=2.9 rad/s;(c)ω=4.6 rad/s;(d)ω=6 rad/sFig.8.Influence of base amplitude on the amplitude of system(SP,the static bifurcation point;HP,the Hopf bifurcation point):(a)ω=2.3 rad/s;(b)ω=2.9 rad/s;(c)ω=4.6 rad/s;(d)ω=6 rad/s.

图9 弹簧摆响应随基础振幅变化的分岔图和李雅普诺夫指数(ω=2.9 rad/s,Ab=0.3 m时的初值为(−0.30,0.34,−0.54,0.43),仿真时间τ=0—800π)Fig.9.Bifurcation diagram and Lyapunov exponent of spring pendulum with the change of base amplitude(ω=2.9 rad/s;the initial value is(−0.30,0.34,−0.54,0.43)when Ab=0.3 m;simulation time is τ=0–800π)

图10 弹簧摆随基础振幅变化的典型动力学行为的庞加莱映射 (a)周期1运动,Ab=0.32 m;(b)拟周期运动,Ab=0.34 m;(c)拟周期运动,Ab=0.366 m;(d)混沌,Ab=0.368 m;(e)周期4运动,Ab=0.372 m;(f)拟周期运动,Ab=0.374 m;(g)周期16运动,Ab=0.3752 m;(h)周期11运动,Ab=0.38 m;(i)混沌,Ab=0.384 m;(j)拟周期运动,Ab=0.4454 m;(k)周期7运动,Ab=0.45 m;(l)混沌,Ab=0.485 mFig.10.Poincare map of typical dynamic behavior of spring pendulum with the change of base amplitude:(a)Period 1 motion,Ab=0.32 m;(b)almost periodic motion,Ab=0.34 m;(c)almost periodic motion,Ab=0.366 m;(d)chaos,Ab=0.368 m;(e)period 4 motion,Ab=0.372 m;(f)almost periodic motion,Ab=0.374 m;(g)period 16 motion,Ab=0.3752 m;(h)period 11 motion,Ab=0.38 m;(i)chaos,Ab=0.384 m;(j)almost periodic motion,Ab=0.4454 m;(k)period 7 motion,Ab=0.45 m;(l)chaos,Ab=0.485 m.

表2 图8中的分岔类型和Floquet乘子的变化Table 2.Bifurcation type and change of Floquet multiplier corresponding to Fig.8.

为了了解系统响应在Hopf分岔后随基础振幅的变化,我们利用龙格-库塔方法对系统进行数值求解.图9给出了响应随基础振幅变化的分岔图和李雅普诺夫指数图,可以看到系统响应随基础振幅的变化出现了倍周期运动、拟周期运动和混沌等复杂的响应形式.图10给出了典型动力学响应的庞加莱映射,可以看到当系统发生Hopf分岔后,响应从周期1运动变为拟周期运动,随着基础振幅的增大,拟周期运动出现环面倍化(见图10(c)),进而环面发生破裂,系统响应进入混沌(见图10(d)).随着基础振幅的进一步增加,系统响应退出混沌,变为周期4运动(见图10(e)),然后通过Hopf分岔成为4个吸引不变环的拟周期运动(图10(f))和周期16运动(图10(h)).基础振幅继续增加,系统响应出现了周期11运动,然后通过阵发性进入混沌(见图10(i)).当基础振幅继续增大时,系统的响应以混沌为主,只是在Ab=0.445—0.485 m之间,系统响应在周期7运动、7个吸引不变环的拟周期运动和混沌之间出现了两次切换.

综合上面的分析,我们给出了基础运动频率-振幅平面上周期解的转迁,可以看到静态分岔边界、Hopf分岔边界和旋转解边界将参数平面分成了7个保持域,其中参数域②是拟周期运动、混沌以及复杂周期运动的分布域,参数域①内系统是唯一的周期运动,而参数域⑥内为旋转解.图中阴影部分,即区域③,④,⑤,⑦,是初值敏感区域,即通常所说的双稳态区域,对应不同的初值,系统可能收敛于不同的稳态运动.其中区域③和④对应不同的初值,系统将收敛到振幅不同的周期解,而对于参数域⑤和⑦,当初值较小时,系统的响应为振幅较小的周期运动,当初值较大时,系统的响应将会是连续的旋转运动.

图11 基础运动频率-振幅平面上周期解的转迁集(BS,静态分岔边界;HF,Hopf分岔边界;BR,旋转解边界)Fig.11.Transition sets of the response on the base motion parameters plane(BS,boundary of static bifurcation;HF,boundary of Hopf bifurcation;BR,boundary of continuous rotational motion).

6 结 论

本文针对基础水平运动的弹簧摆开展研究,利用拉格朗日方程建立了系统动力学方程.将离散傅里叶变换、谐波平衡法以及同伦延拓方法相结合对系统的周期响应进行求解,突破了传统方法使用泰勒展开导致的小振幅的限制,与数值计算结果的对比表明本文的求解方法具有较高的精确度.

研究了基础运动的频率和振幅对系统周期响应的影响,发现基础频率对系统振幅的影响表现为双峰,当基础振幅较大时,在两个峰值附近会发生跳跃现象.周期解振幅随基础振幅的增大而增大,对应某些基础频率,周期解的振幅随基础振幅的变化也会发生跳跃.对应某些基础频率和振幅,弹簧摆可能出现连续旋转运动,同时呼吸方向的振幅极大.基于上述结果,给出了基础运动参数平面上响应形式的转迁.

对应某些基础频率和振幅,系统的周期响应可能发生Hopf分岔,利用数值仿真研究了Hopf分岔后响应的变化,发现系统出现了倍周期运动、拟周期运动和混沌等复杂响应形式.研究表明系统进入混沌主要是通过拟周期环面破裂和阵发性.