基于自适应阈值方法实现迭代降噪鬼成像∗

周阳 张红伟 钟菲 郭树旭

1)(吉林大学电子科学与工程学院,集成光电子学国家重点实验室,长春 130012)

2)(长春工程学院电气与信息工程学院,长春 130012)

(2018年6月27日收到;2018年8月29日收到修改稿)

为了有效降低传统鬼成像中相关噪声对成像质量的影响,本文提出一种基于最佳阈值的迭代降噪鬼成像.首先在迭代降噪鬼成像的基础上,采用自适应阈值迭代法,在不需要目标先验信息的前提下,找到一个逼近传统鬼成像中相关噪声的阈值,根据得到的阈值构造噪声干扰项.为了每次迭代初值更接近原始目标的透射系数,对其进行二值化,降低重构图像背景噪声对迭代性能的影响.仿真以及实验结果表明,本文提出的方法与传统方法相比,视觉效果以及峰值信噪比值有明显提高.

1 引 言

关联成像又被称为鬼成像(ghost imaging,GI),是一种新颖的成像技术,利用两束光的强度关联性实现目标重构.其中一束光作为探测光束,包含目标信息,由无空间分辨率的桶探测器接收,另一束光作为参考光束,直接被有空间分辨率的探测器接收.与传统光学成像技术相比,GI的突出特点在于可实现无透镜成像以及抗湍流干扰,在信息安全、遥感、生物医学等领域有广泛的应用价值[1−6],是近年来量子光学[7−10]以及经典光学成像中的研究热点[11−13].

最早由Klyshko[8]提出基于纠缠光子对的方案,随后由Pittman等[9]完成第一个GI实验.随着GI技术的发展,相关理论以及实验证明,纠缠光源并不是关联成像的必要条件,通过经典的热光源也能实现GI.然而,庞大的测量次数以及低信噪比制约了传统GI技术在实际中的应用.近年来,为了改善GI质量,提出了许多改进方法,如差分鬼成像(differential ghost imaging,DGI)[14],归一化鬼成像(normalized ghost imaging,NGI)[15],压缩感知鬼成像(compressive ghost imaging,CGI)[16−19]以及其他改进方法[20−27].在相同的测量次数下,相比DGI,NGI等方法,CGI在提高成像质量方面优势明显,然而CGI自身的优化过程是耗时的,并且对处理器性能要求较高.伪逆关联成像(pseudoinverse ghost imaging,PGI)[21,22]虽然能够快速实现高分辨率成像,但在实际应用中,抗噪性能较差,不能获得稳定的重构目标.文献[23]提出了一种迭代降噪鬼成像(iterative denoising of ghost imaging,IDGI)方法,该方法能够获得高信噪比图像,但是阈值的选取方法并不具有实际通用性.文献[24]提出伪逆迭代降噪鬼成像(pseudo-inverse iterative denoising of ghost imaging,PIGI),较PGI效果有一定提升,但PIGI方法的实现,须以PGI能够获得更接近于目标的透射系数为前提,由于PGI重构结果易受噪声干扰,因此会影响迭代降噪性能,并且PIGI的阈值选取方法同样不具普适性.文献[25]在NGI的基础上提出了一种自适应阈值迭代降噪的思想,但是在阈值选取的过程中,仍需要参考目标验证合适的阈值.文献[26]在对应NGI的基础上提出迭代降噪归一化鬼成像(iterative normalized correspondence ghost imaging,INCGI),呈现了较好的重构效果,但是没有讨论阈值对迭代降噪性能的影响.

与上述方法不同,为了降低测量次数以及提高成像信噪比,本文提出一种自适应阈值方法实现IDGI方案,在不需要目标先验知识的基础上,通过自适应阈值方法完成GI中与相关噪声有关的阈值计算,根据得到的阈值完成噪声干扰项的构造,结合IDGI的降噪模型,经过3次迭代降噪即可抑制相关噪声对GI质量的影响,最终实现重构目标信噪比的提高.同时,为了使每次迭代值更接近目标的透射系数,对归一化后的目标透射系数进行二值化,可进一步提高迭代降噪的性能.仿真以及实验结果表明,本文提出的方法相对于传统GI方法,重构图像的背景噪声被明显抑制.

2 方法理论以及仿真分析

图1为本文采用的GI实验示意图,激光器发出的光经过透镜L2以及L3放大后,通过缓慢旋转的毛玻璃,产生赝热光源.赝热光经过分束棱镜(beam splitter,BS)后,被分为参考光束以及探测光束两束相同的光.参考光束直接被电荷耦合器件(charge coupled device,CCD)接收,记为IR,探测光束被物体调制后,再经过透镜L1后,被无空间分辨率的桶探测器接收,记为IB.

根据文献[11],在传统关联成像系统中,去除背景的关联函数公式为

其中,M代表总测量次数;(x)表示第i次测量中,参考探测器CCD上点x处的光强;=为第i次测量时,桶探测器得到的

光强值;O(x)表示目标的透射系数/反射系数.对进行进一步分析,如(2)式:

其中,δ2(x,x)表示自相关系数,δ2(x,x1)表示互相关系数.

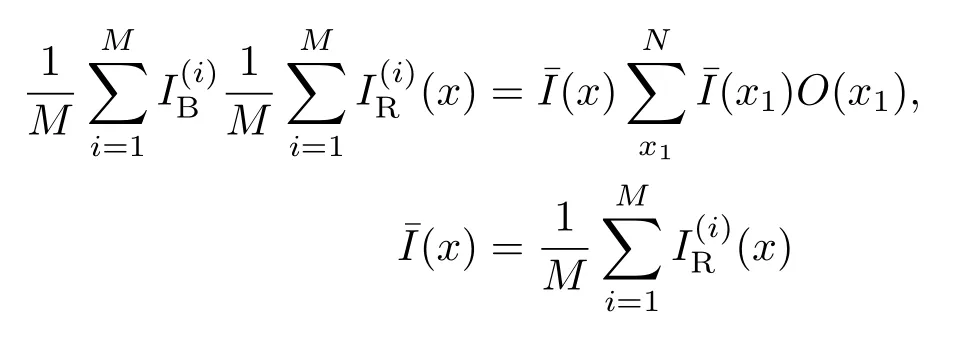
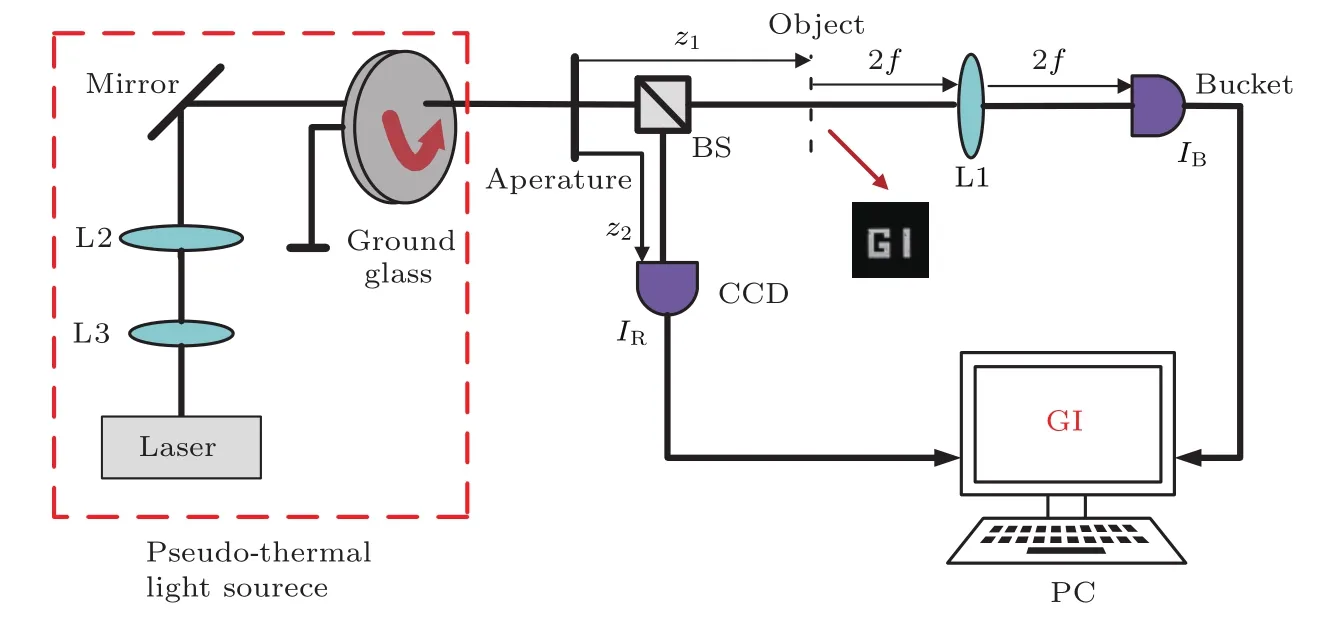
图1 基于赝热光的GI实验示意图(BS,分束棱镜;PC,计算机;z1,目标与光源之间的距离;z2,CCD与光源之间的距离)Fig.1.Experimental schematic of GI with pseudo-thermal light.BS,beam splitter;PC,personal computer;z1,the distance between the light source and the object;z2,the distance between the light source and the CCD.

表示在像素点x处的平均光强值,总像素点的大小为N.假设像素各点的光强是相互独立变化的,则有δ2(x,x1)=0,因此,成像公式可以简化成∆G(2)(x)=δ2O(x),其中δ2(x,x)=δ2.但是在实际的应用中,由于有限的测量次数以及噪声等因素的影响,导致各像素点之间存在相关性噪声,即δ2(x,x1)=0.

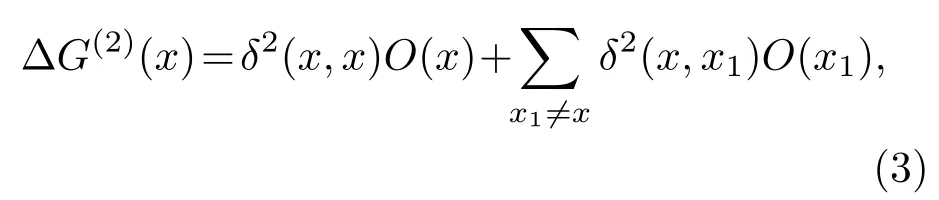
其中,δ2(x,x1)的存在是造成GI重构图像信噪比低的关键因素,虽然相关噪声值很小,但是会最终影响GI效率.正如IDGI方法以及文献[27]所描述的,去除δ2(x,x1)较小值,能够提高成像信噪比.根据IDGI,迭代降噪公式为

其中,δ′(x,x1)为通过设定阈值构造的噪声干扰项;s表示迭代次数,当s=1时,IDGI(s−1)(x1)为传统方法重构出的目标透射系数/反射系数.由于NGI以及DGI效果近似,为了与IDGI算法原理一致,本文同样以DGI重构出目标的透射系数作为初始迭代值.下一次迭代时,则以上一次的迭代结果作为目标透射系数继续迭代降噪,一般经过3次迭代后可获得高信噪比图像.在IDGI方法中,δ′(x,x1)构造过程如下:

其中,t′为归一化后的阈值,取值范围[0,1].但是,t与t′是未知的两个变量,需要设定初始阈值t′,通过已知参考目标,确定与噪声干扰项逼近的阈值t的大小.如何在不需要先验知识的基础上,实现噪声干扰项的构造,是IDGI方法满足工程实际应用的关键.本文采用一种自适应阈值的方法,在不需要参考目标的情况下,实现噪声干扰项有关阈值的选取.为了方便说明,首先对(4)式进行重新改写.

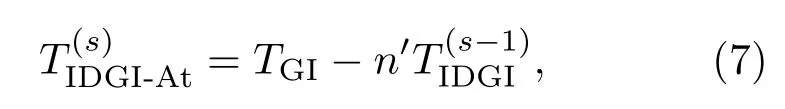
其中,TGI为GI重构的目标系数,以列向量的形式表示;n′为构造的噪声干扰项;当s=1时,为DGI重构的目标透射系数,同样以列向量的形式表示.在M次测量下,获得的散斑场逐行排列可得到测量矩阵Φ:

这里,协方差矩阵COV(Φ)的对角以及非对角元素分别对应自相关系数δ2(x,x)以及互相关系数δ2(x,x1).进一步对协方差矩阵的非对角元素进行归一化:

其中,Φ′c表示协方差矩阵COV(Φ)非对角元素,δ2max表示max{δ2(x,x1)}. 假设,n(x,x1)是n在(x,x1)上的值,求出n中的最大值nmax以及最小值nmin,将nmax以及nmin相加求平均,求得初始迭代阈值T0,即T0=(nmax+nmin)/2.通过T0将n分为大于T0以及小于T0两部分,分别求出两部分的期望值,取两部分期望值的均值为新的阈值T1.经过k次迭代后,|Tk+1−Tk|足够小时,此时t′′=Tk+1为最佳阈值.

当阈值为Tk时,小于阈值以及大于阈值两部分的期望值求解如下:

其中,nb(Tk)与nc(Tk)分别为小于阈值Tk以及大于阈值Tk两部分的期望值,p(x,x1)表示(x,x1)点处值为n(x,x1)的概率

其中,ψ[·]和φ[·]分别为计算协方差矩阵中协方差系数等于n(x,x1)的元素个数和协方差矩阵的整体元素个数.

为了降低迭代次数,当满足条件|Tk+1−Tk|<0.001时,停止迭代计算,Tk为最佳阈值. 将t′′=Tk代入(13)式中,实现点(x,x1)处噪声干扰项n′(x,x1)的构造.

通过(13)式,可以将相关噪声从协方差矩阵COV(Φ)中分离出来,实现噪声干扰项的构造.因此(4)式重新定义为

为了验证本文提出方法的有效性,在5400次仿真测量次数下,采用不同重构方法对二值图像“Z”进行重构,归一化结果如图2所示.

图2(b)—(e)分别对应GI,DGI,IDGI以及IDGI-At方法的重构图像.如果直接设t′=0.5,在视觉上,基于IDGI-At的重构图像分辨率要好于IDGI方法,这说明本文提出的阈值方法对于相关噪声干扰项的选取是有效的.正如图2(f)所示,IDGI-AT的重构图像的背景噪声相对于IDGI-At被进一步去除,这说明对于数字掩膜目标,透光部分的像素点对应为1,不透光部分像素点对应为0,对每次迭代初值进行二值化,可更接近原始目标的透射系数,这是重构图像背景噪声被进一步移除的根本原因.为了更好地对比成像效果,将采用峰值信噪比(peak signal-to-noise ratio,PSNR)衡量重构图像质量,其定义如下:

其中,MAXI表示图像颜色的最大数值,8位采样点表示255.MSE为原始目标图像与重构目标图像的均方误差.

图2 目标字母“Z”的仿真结果对比 (a)原始目标;(b)GI的重构图像,PSNR=10.72 dB;(c)DGI的重构图像,PSNR=13.54 dB;(d)t′=0.5时,IDGI的重构图像,PSNR=15.44 dB;(e)IDGI-At的重构图像,PSNR=16.92 dB;(f)IDGI-AT的重构图像,PSNR=19.0227 dBFig.2.Simulation demonstration of reconstruction results for letter “Z”:(a)Original object;(b)GI reconstruction image,PSNR=10.72 dB;(c)DGI reconstruction image,PSNR=13.54 dB;(d)t′=0.5,IDGI reconstruction image,PSNR=15.44 dB;(e)IDGI-At reconstruction image,PSNR=16.92 dB;(f)IDGI-AT reconstruction image,PSNR=19.0227 dB.

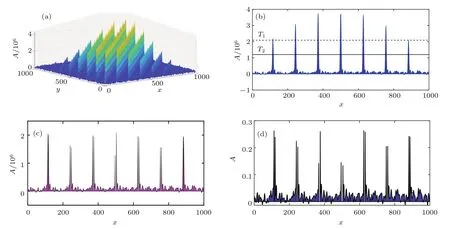
图3 不同阈值方法下噪声干扰项构造 (a)矩阵部分三维图,x与y分别表示矩阵的横坐标以及纵坐标,A表示的幅值;(b) 矩阵的部分截面图,y=500,x=1,2,···,1000;(c)T1=t,小于阈值 T1 的截面图;(d)T2=t′′×,小于阈值T2的截面图Fig.3.Noise interference construction based on di ff erent thresholds:(a)Calculated results for the part region of matrix.The x and y represent the row and column coordinate respectively.The A denotes the amplitude of;(b)the partial sectional view of the matrix,y=500,x=1,2, ···,1000;(c)T1=t,corresponding to the part less than T1in(b);(d)T2=t′′× ,corresponding to the part less than T2in(b).

图4 目标字母“Y”的仿真结果对比 (a)原始目标;(b)GI的重构图像,PSNR=12.94 dB;(c)DGI的重构图像,PSNR=15.44 dB;(d)t′=0.5时,IDGI的重构图像,PSNR=16.06 dB;(e)IDGI-At的重构图像,PSNR=18.07 dB;(f)IDGI-AT的重构结图像,PSNR=20.8274 dBFig.4.Simulation demonstration of reconstruction results for letter“Y”:(a)Original object;(b)GI reconstruction image,PSNR=12.94 dB;(c)DGI reconstruction image,PSNR=15.44 dB;(d)t′=0.5,IDGI-At reconstruction image,PSNR=16.06 dB;(e)IDGI-At reconstruction image,PSNR=18.07 dB;(f)IDGI-AT reconstruction image,PSNR=20.8274 dB.

图2 (b)—(f)中图像对应的PSNR值分别为10.72,13.54,15.44,16.92以及19.0227 dB.IDGIAt重构图像的PSNR值高出阈值为0.5的IDGI方法1.48 dB,同时,IDGI-AT重构图像PSNR值要高出IDGI-At方案2.1027 dB.

图3为不同阈值方法下噪声干扰项构造,沿着图3(a)的箭头方向,取矩阵的截面图,如图3(b)所示,图3(c)对应图3(b)中小于虚线的部分,图3(d)对应图3(b)中小于实线的部分.正如图2(d)和图2(e)所示,IDGI-At重构图像的PSNR值要高于IDGI方法,主要原因是采用的自适应阈值方法在噪声干扰项构造过程中,有效地去除了{δ(x,x1)}值较大的部分,因此构造的噪声项更接近于GI中的噪声项,通过迭代消去有效地移除重构图像背景噪声.

为了证明本方法对不同目标的有效性,下面更换重构目标,对二值图像“Y”进行仿真,基于不同方法的重构图像结果如图4所示.

图5 不同测量次数下重构图像的PSNR值拟合曲线对比(黑色带方角形的实线代表IDGI-AT的PSNR值拟合曲线,紫色带棱形的实线代表IDGI-At的PSNR值拟合曲线,绿色带星形的实线代表IDGI-0.5的PSNR值拟合曲线,红色带圆形的实线以及蓝色带三角形的实线分别代表DGI以及GI重构图像PSNR值拟合曲线)Fig.5.The PSNRs of GI,DGI,IDGI-0.5,IDGI-At and IDGI-AT for different number of measurements.Black solid curve with squares shows IDGI-AT reconstruction results.Purple solid curve with diamonds indicates IDGI-At reconstruction results.Green solid curve with stars shows IDGI-0.5 reconstruction results.Red solid curve with rings and blue solid curve with triangles correspond to DGI and GI reconstruction images respectively.

如图4所示,在5400次测量次数下,基于IDGI-At方法重构出的图像较阈值为0.5的IDGI方法具有更好的清晰度,图像的背景噪声被进一步去除,基于GI,DGI,IDGI以及IDGI-At方法的重构结果的PSNR值分别为12.94,15.44,16.06以及18.07 dB.IDGI-At方法相对于DGI方法提高2.63 dB,较IDGI方法提高2.01 dB.正如图4展示的结果,IDGI-AT重构图像的背景噪声明显被去除,相对于IDGI-At方法,PSNR值提高2.7574 dB.为了分析本文提出方法的可靠性,下面对不同测量次数(2000—5400)下GI,DGI,IDGI-0.5,IDGI-At以及IDGI-AT五种成像方法重构图像的PSNR值进行定量比较,结果如图5所示.

如图5所示,在2000—5400次测量次数下,IDGI-AT方法要好于IDGI-At,IDGI-0.5,DGI以及GI方法.如IDGI-0.5在低测量次数(M=2500)时,成像质量较DGI变差,而IDGI-At较DGI以及IDGI-0.5提高明显.而IDGI-AT(M=2000)重构图像的PSNR值要明显高于IDGI-At(M=5400),基于IDGI-AT方法重构图像的PSNR值为18.76 dB,而IDGI-At重构图像的PSNR值为18.04 dB.这些定量的仿真结果表明,IDGI-AT的PSNR值有所提升.虽然本文方法在阈值计算过程中可能消耗更多时间,但是与相关噪声有关的阈值可直接通过散斑场的信息求取.因此,在5400次测量次数下,实际成像时间仅高出IDGI方法约0.8 s,多出的微小时间差可以通过提高实验电脑的配置而进一步缩小.表1列出了DGI,IDGI以及IDGI-AT方法性能的比较.

表1 三种成像方案的性能比较Table 1.Performance comparison of three imaging schemes.

3 实验平台测试以及结果分析

为了验证本文提出方法的实际可行性,根据图1的GI实验原理图完成实验系统的搭建.激光器(波长λ=532 nm)发出的光束经过透镜L2,L3后,通过缓慢旋转的毛玻璃形成赝热光源,赝热光被分束棱镜50:50分成两束相同的光,一部分为探测光束,经过物体调制后,经过透镜L1被物臂上的桶探测接收.另一部分光为参考光束,被参考臂上的探测器直接接收.赝热光源与目标以及与参考探测器之间的距离分别由z1以及z2表示,这里z1=z2=200 mm.f表示透镜的焦距,f=150 mm.参考探测器采用的CCD(Stingray F-504,AVT,Germany)分辨率约为3.45µm×3.45µm.因为对CCD采集的光强度分布进行求和可获得总光强度,所以实验中采用等同的CCD代替桶探测器.成像目标“GI”大小为128×128 pixels.在本次实验中,用于图像重构的计算机为华硕台式电脑(CPU:Intel core is i7-7700,3.60 GHz,16 GB),总测量次数为5400次,图6为不同方法下目标“GI”的重构结果对比.

如图6所示,实验结果与理论的仿真结果一致,在视觉上,IDGI-At的重构图像要好于GI,DGI以及IDGI方法,基于IDGI-At的重构图像的背景噪声在一定程度上被去除.在5400次测量次数下,IDGI-At方法重构图像的PSNR值为15.37 dB,DGI的PSNR值为13.09 dB,IDGI-At的PSNR值较DGI提高2.28 dB,相对于GI提高3.83 dB.同时,IDGI-AT的PSNR值可达17.0783 dB,与视觉观察效果一致,与其他几种成像方法相比,重构图像的背景噪声被明显抑制.

图7给出了2000—5400次测量次数下,GI,DGI,IDGI-0.5,IDGI-At以及IDGI-AT五种重构方法的PSNR值曲线拟合结果.本文提出的方法在相同测量次数下,明显高出GI,DGI,IDGI-0.5以及IDGI-At方法图像的PSNR值,随着测量次数的增加,PSNR值逐渐提高.

图6 目标“GI”实验结果对比 (a)原始目标;(b)GI方法的重构图像,PSNR=11.54 dB;(c)DGI的重构图像,PSNR=13.09 dB;(d)t′=0.5时,IDGI的重构图像,PSNR=14.24 dB;(e)IDGI-At的重构图像,PSNR=15.37 dB;(f)IDGI-AT的重构图像,PSNR=17.0783 dBFig.6.Experimental demonstration of reconstruction results for letter “GI” object:(a)Original object;(b)GI reconstruction image,PSNR=11.54 dB;(c)DGI reconstruction image,PSNR=13.09 dB;(d)t′=0.5,IDGI reconstruction image,PSNR=14.24 dB;(e)IDGI-At reconstruction image,PSNR=15.37 dB;(f)IDGI-AT reconstruction image,PSNR=17.0783 dB.

图7 不同测量次数下重构图像的PSNR值曲线拟合结果(黑色带方形的虚线代表IDGI-AT的PSNR值拟合曲线,紫色带棱形的虚线代表IDGI-At的PSNR值拟合曲线,绿色带星形的虚线代表IDGI-0.5的PSNR值拟合曲线,红色带圆形的点线以及蓝色带三角形的虚线分别代表DGI以及GI重构图像PSNR值拟合曲线)Fig.7. The PSNR of GI,DGI,IDGI-0.5,IDGIAt and IDGI-AT for different number of measurements.Black dashed curve with squares represents IDGI-AT reconstruction results.Purple dashed curve with diamonds indicates IDGI-At reconstruction results.Green dashed curve with stars shows IDGI-0.5 reconstruction results.Red dashed curve with rings and blue dashed with triangles correspond to the DGI and GI reconstruction results.

4 结 论

综上所述,本文在IDGI的基础上,提出基于最佳阈值的IDGI方案.采用最佳阈值的方法,在不需要目标先验信息的前提下,找到与噪声干扰项有关的最佳阈值,在迭代降噪方法的基础上,将每次迭代初值进行二值化,再进行进迭代降噪,经过三次迭代后,可获得高质量重构图像.仿真以及实验结果表明,本文提出的方法是可行的,相对于GI,DGI以及IDGI方法,IDGI-AT重构图像具有更高的分辨率以及PSNR值.但本文只对二值图像进行仿真以及实验验证,对于灰度图像实现迭代降噪GI方法将会是我们未来的研究任务.