基于异构模型的铁路出发旅客衔接时间价值

朱 海，罗 霞*,b，陈 欣，刘永红

(西南交通大学a.交通运输与物流学院；b.综合交通运输智能化国家地方联合工程实验室，成都611756)

0 引言

铁路出发旅客衔接时间是旅客从出发地前往铁路客运站乘车过程中所花费的时间，可包括衔接交通等候时间和车内时间，是旅客衔接方式选择的重要影响因素，也是枢纽衔接系统供给与旅客衔接服务需求交互的重要媒介.衔接时间价值作为单位衔接时间的货币化描述，在枢纽建设与管理的成本—效益分析中有着较为广泛的应用.因此，开展衔接时间价值研究对实现铁路枢纽衔接系统精细化管理有着十分重要的意义.

时间价值的求解多结合非集计模型和支付意愿法进行[1].理论方面，Wardman等[2]采用元分析法对1963—2011年间欧洲地区389篇时间价值相关文献进行了研究，发现时间类型、GDP、出行距离、出行目的、交通方式、标定方法等因素对时间价值测算结果具有影响；Small[3]回顾了1965—2012年间通勤时间价值的相关研究，梳理了收入、出行目的、出行时刻、行程计划、可靠性、出行信息等因素对时间价值测算的影响；Hess等[4]讨论了ML模型参数分布对时间价值求解结果的影响，指出影响主要源于其参数分布假设的尾部差异.实证方面，Landau等[5]基于MNL模型研究了航空旅客在不同出行目的和收入分组下的出发衔接时间价值、机场内部时间价值及与航班行程相关的其他时间价值；陈旭梅等[6]采用考虑了收入变量的MNL模型对北京市公共交通出行时间价值进行了估计；李晓津等[7]采用ML模型测算了京津冀地区的旅客区域出行时间价值.

总结发现，现有研究多采用单一模型，少有的异构模型时间价值比较研究对各类偏好异质性非集计模型的求解结果比较不够充分；同时，现有研究多面向城市通勤交通、航空枢纽，专门针对铁路出发旅客衔接行程时间价值的研究较少.鉴于此，本文建立铁路出发旅客衔接方式选择的异构模型，结合成都东客站SP调查数据，在相同数据环境下对不同模型结构下的旅客个人和样本总体衔接行程等候时间价值和车内时间价值进行求解和比较，以期为铁路枢纽衔接系统优化提供支撑.

1 时间价值模型

1.1 支付意愿法

从消费行为理论看，衔接行程时间消耗和费用支出可视为具有相互替代性的“效用”.令xk表示衔接行程时间的相关属性，对应参数为βk；xm为费用属性，对应参数为βm；Vnsi为试验情景s中选择枝i对受访者n的可观察效用.则受访者n在情景s下选择第i个选择枝时的个人时间支付意愿和样本总体时间支付意愿分别为

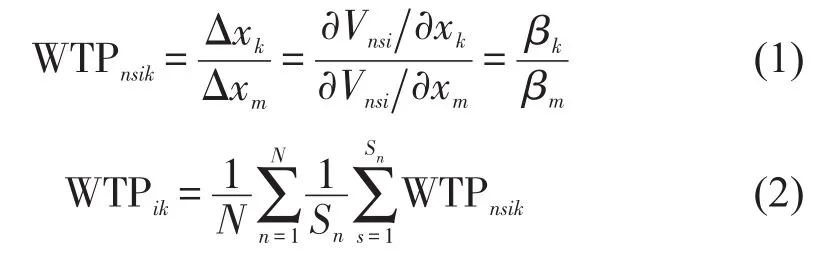
1.2 异构模型

式(1)中βk与βm的求解多基于非集计模型.设旅客n对选择枝j的效用函数可通过不可观测项εj、选择枝j中第k个可观测属性Xjk(包括选择枝属性、个人经济属性等)及其对应参数βnjk的线性关系表示.进一步通过属性k的期望参数值βjk、围绕βjk的离差σjk，以及根据βnjk先验分布的随机抽样vnjk对βnjk进行展开，可得Unj的表达式为

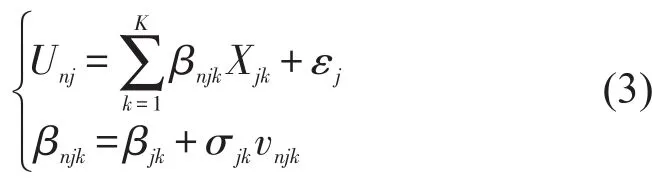
假设εj在不同选择枝间相互独立且服从I型极值分布可导出Logit模型.根据vnjk的不同假设可进一步导出同质、连续异质、离散异质3类属性偏好模型.近年来有研究人员尝试在离散异质偏好模型中添加旅客对于Xjk处理异质性的表达，演变出复合异质模型.具体地：

(1)同质偏好MNL模型.

假设vnjk≡0，即旅客对选择枝属性具有相同偏好，此时βnjk退化为βjk，从选择枝备选集中选择第i个选择枝的概率为[8]

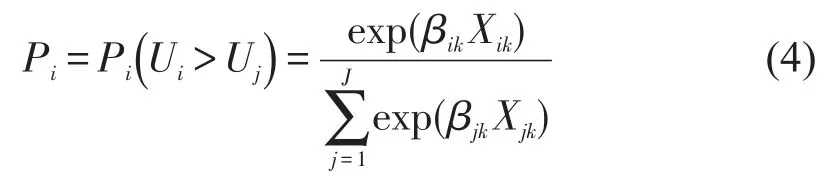
(2)连续异质偏好ML模型.

假设vnjk服从连续型分布，此时不同旅客的属性偏好满足对应分布假设下的随机抽样，选择枝i的概率Pni是MNL选择概率在参数联合密度函数上的积分.将可观察属性及其参数以向量形式表示，得到Pni的表达式[9]为

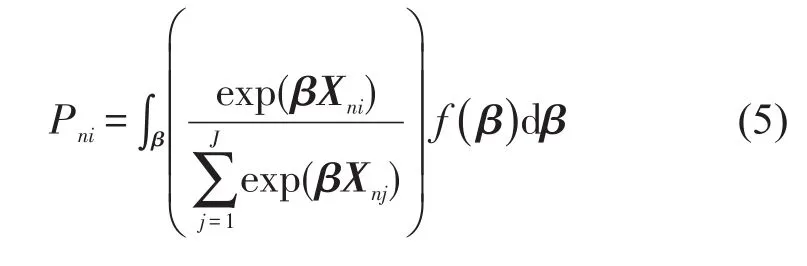
(3)离散异质偏好潜在类别模型(LCL).

假设vnjk服从离散型分布，此时旅客对各属性的异质偏好存在于有限个的潜在类别c中.c对于模型而言属于非参数，需在建模时予以假设.选择枝i的选择概率Pni是各类别c中MNL选择概率Pni|c与相应潜在类别概率Hnc乘积的离散加和，如式(6)[10]所示.属性参数β(β1,β2,…,βc)为各潜在类别属性参数的集合，Hnc的先验分布假设采用MNL概率形式.

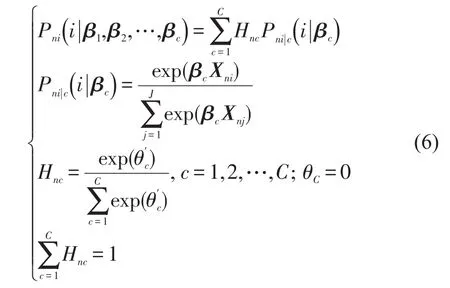
(4)复合异质性模型(Hybrid).

模型属性Xjk是建模人员根据经验的假设，旅客可能根据自身属性信息接收能力和处理习惯的不同对属性采取差异化处理.譬如，只考虑Xjk中的某些属性(属性忽略处理规则，ANA)，或将等候时间和车内时间的总和作为衔接方式比选标准(同量纲属性合并处理规则，ACMA).将拥有不同处理规则的旅客划分为全属性(FAA)、忽略属性(ANA)、全属性且合并处理(ACMA)、忽略属性且合并处理(ACMA-ANA)等4个潜在类别，各自分类数为R、G、Q、W，式(3)中Unj可进一步表示为

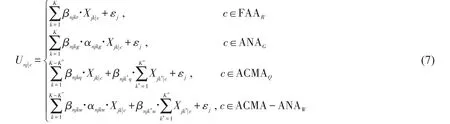
式中：|c表示隶属分类；K∗为具有ACMA特征的属性标号；为合并处理后属性对应的参数；αnjk为旅客n对选择枝j中属性k的考虑指示变量，考虑时取1，否则取0.

将式(7)带入式(6)，即在LCL中加入旅客对Xjk处理异质性的表达，可得到复合异质性模型.上述模型的参数估计均可采用极大似然函数估计法并结合Newton-Raphson算法求解.

2 SP调查与模型标定

2.1 问卷设计与回收

面向成都铁路东客站出发旅客开展SP调查，考虑“常规公交、城市轨道交通、出租车、私家车、网约车”5种衔接方式，属性及取值如表1所示.采用基于真实水平的属性水平设置技术，结合《成都市交通发展年报》等统计数据对具体试验情景下的各方式现状水平值进行取值.属性编码方面，Deptime以夜间时刻为基础水平，引入虚拟变量Depta和Deptb进行效应编码(Effects Coding)，有高峰(1,0)，平峰(0,1)和夜间(-1,-1)；Purp和Ttype保留原变量名进行效应编码，有商务(1)，非商务(-1)；高速(1)，普通(-1)；其他属性均采用线性编码.

为提高调查效率采用均匀—效率两阶段小样本试验设计法，将SP情境设计与非集计模型极大似然函数求解进行结合，使得该方法与传统正交设计法相比，在相同样本量下可获得更好的标定效果[11].预调查使用48情景均匀设计表，在DPS软件(版本7.05)中采用定向优化算法编程实现；第2阶段使用的24情景D-efficient效率设计表，在Ngene软件(版本1.1.2)中采用swap算法编程实现.预调查阶段通过网络平台共收集30套、120位受访旅客的1 440条有效决策信息，用于效率设计所需参数先验值标定；选取第2阶段获得的170套来自510位受访旅客的4 080条决策信息用于模型正式标定.

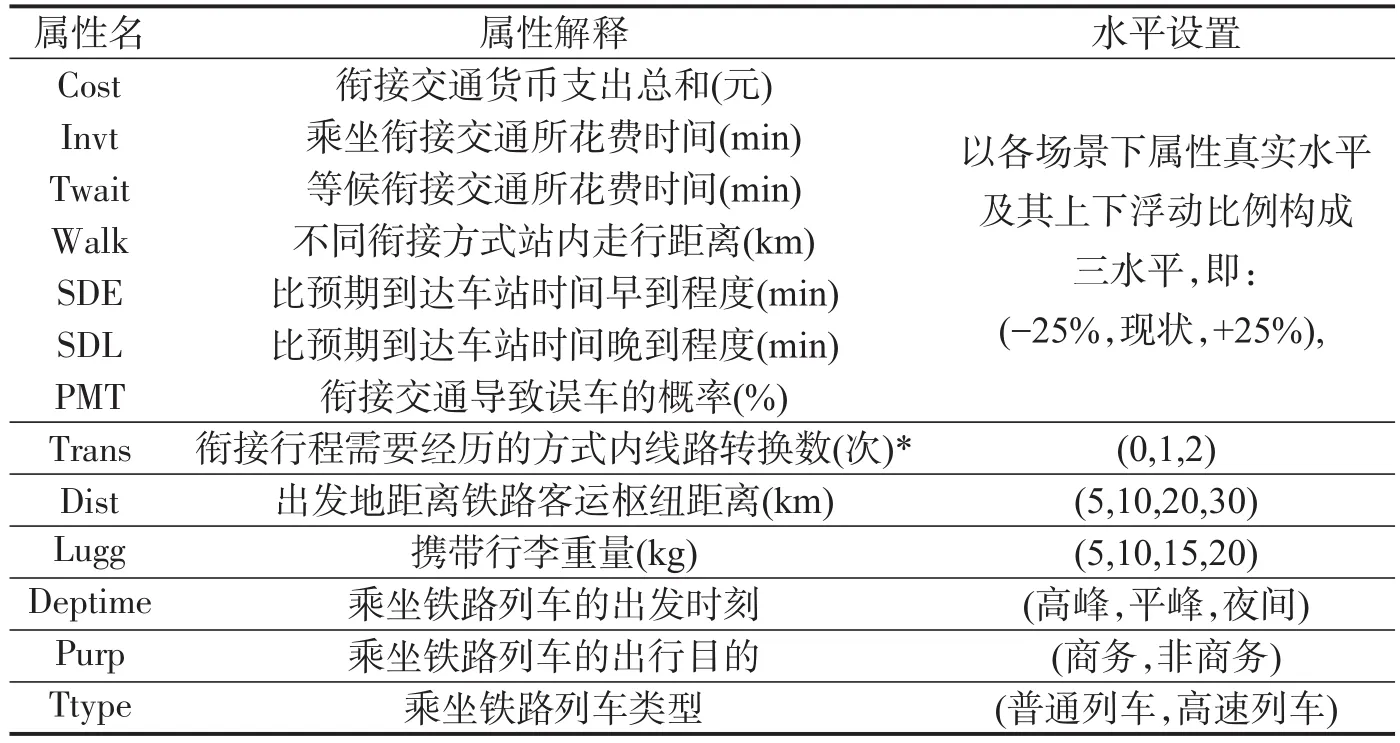
表1 SP试验设计属性水平设置Table 1 Attributes explanations and levels in SP design

第2阶段中对受访旅客的社会经济特征数据(SDC)进行了采集，如表2所示.女性受访人数略多于男性，比例约为1.22∶1.00；年龄分布主要集中在中青年段；月收入主要集中在3 000元以下和[3 000,6 000)元两个区段；本市居民与非本市居民分别占比42.75%和57.25%.由于SDC均为分类变量，引入虚拟变量(g end),(a g ea,ageb,agec),(r e si),(incoa,incob,incoc)进行了效应编码.

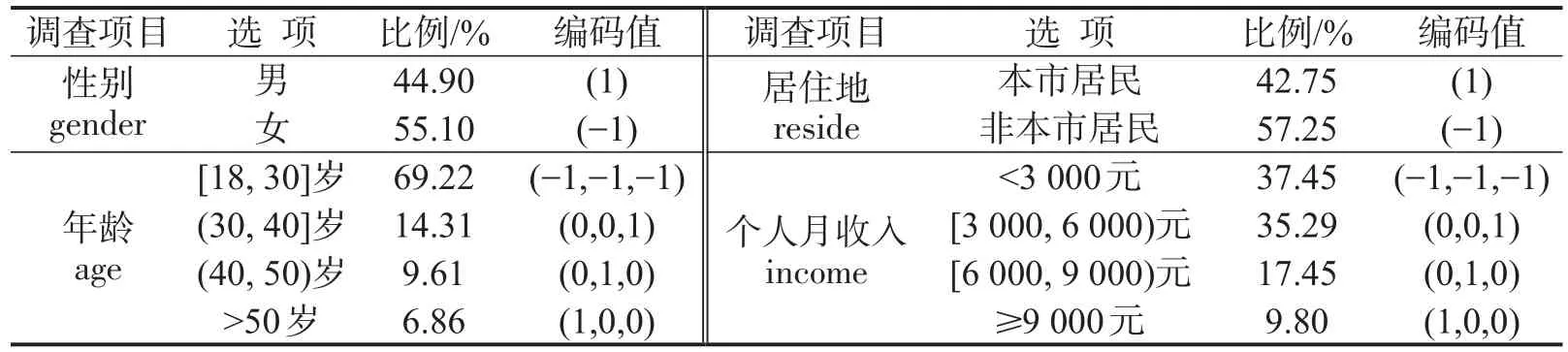
表2 受访旅客SDC属性结构比例与效应编码值Table 2 SDC structure and its effects coding values of railway passengers in survey

2.2 模型设置与标定

根据1.2节建立8种异构模型如表3所示.模型1为MNL；模型2～模型6为以βTwait、βCost、βInvt、βTrans、βSDE、βSDL、βPmt、βWalk、βDist、βLugg为随机参数，具有不同参数分布结构假设的ML；模型7为LCL-2；模型8为基于LCL-2及拟合测试，选取以Dist和Ttype为ANA，βTwait=βInvt为ACMA的Hybrid.

采用第2阶段SP调查数据对模型1～8进行参数标定，整理用于拟合效果分析的调整R2、赤池信息指数(AIC/N)N及求解所需时长，如表4所示.发现5种ML及MNL的调整R2和AIC N值相近，但求解时长差异较大.离散模型相较于ML能够在消耗更少求解时间的同时得到更好的拟合效果，Hybrid较ML(O T)在调整R2方面提升了25.52%，且求解时长仅为ML(OT)的1/6；同时，Hybrid通过对属性处理异质性的表达，在相同异质层数(均为2)下使调整R2在LCL-2基础上提升了5.94%.

3 结果分析

3.1 个体时间价值

根据式(1)计算受访旅客个体等候时间价值(VOWT)和车内时间价值(VOIT)并绘制累计频率分布(CDF)如图1和图2所示.MNL的CDF为对应时间价值处的单点未予以展示.

表3 出发旅客衔接方式选择异构模型设置Table 3 Structures of access mode choice models for railway departure passengers

表4 异构模型标定测试统计量比较Table 4 Comparisons on statistical criterions of variation structure models

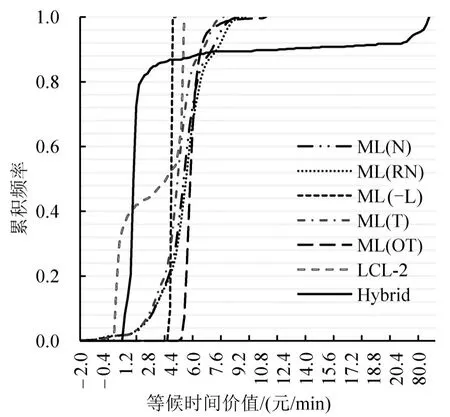
图1 异构模型等候时间价值累计频率分布Fig.1 Cumulative distributions of value of waiting time with variation structure models

从图1看，基于N、RN、T分布的ML模型具有相似的VOWT-CDF形态，且头部均存在负值.这可能与上述分布在坐标原点的对称性有关，即参数抽样可正也可负；从CDF尾部看，ML(T)尾部最短，ML(RN)次之，ML(N)尾部最长；三者首尾以外80%左右的VOWT均介于3.5～7.0元/min.ML(OT)和ML(-L)由于单一的参数符号约束使得求解结果均为正值.ML(OT)有着与ML(T)相似的VOWT-CDF形态但尾部更长；其90%左右的VOWT介于5.0～7.0元/min.ML(-L)所得VOWT集中在4.0～4.5元/min，对应CDF十分陡峭.LCL-2的结果中50%介于0.0～3.5元/min，而另外50%介于3.5～5.0元/min.Hybrid所得VOWTCDF则呈现出较为明显的长尾特性，具有较强的偏态分布特征；约90%的VOWT介于1.0～5.0元/min，而尾部近10%的VOWT介于6.0～80.0元/min及以上.

从图2看，基于N、RN、T分布的ML模型具有相似的VOIT-CDF曲线形态，所得VOIT大致介于2.0～2.6 元/min.ML(OT)求得VOIT中近90%介于2.2～3.0元/min，其CDF曲线有着比ML(T)对应CDF更长的尾部特性.ML(-L)所得VOIT介于2.8～4.0元/min之间，其CDF相较于图1结果较为缓和.LCL-2和Hybrid对应的VOIT-CDF均表现出较为明显的分组特性：LCL-2前50%VOIT介于1.2～1.4元/min，而后 50%VOIT介于1.4～1.8元/min；Hybrid中前50%VOIT介于1.0～1.6元/min，而后50%VOIT介于1.6～2.0元/min.

比较图1和图2可以发现，VOIT总体上小于VOWT，且VOIT在样本总体中的分布更为集中，表明VOWT具有更强的异质性.从各类ML求解结果看，N、RN、T、OT这4种分布分别在图1和图2中呈现出相似形态的曲线特征，说明它们在时间价值求解上具有一定的稳定性.而ML(-L)则表现出较大的差异，这可能源于ML(-L)对参数符号的预先假设与实际结果之间存在偏差.事实上，本文在采用ML(-L)建模时关于βSDE的预先假设为负值，但Hybrid在实际标定中得到了关于βSDE的正值显著结果，反映出旅客认为“提前到达车站能够确保衔接成功”“早到程度具有正向效用”的观点.同时，考虑到ML(N)、ML(RN)、ML(T)在VOWT-CDF曲线头部的负值现象，在5种ML假设中使用ML(OT)求解时间价值较为理想.该发现也与表4中ML(OT)拟合效果优于其他ML模型的结果一致.

3.2 总体时间价值

根据式(2)求解各模型的样本总体时间价值总均值，并计算LCL-2和Hybrid各潜在类别的均值及样本总体中位数值，结果如表5所示.在括号内对LCL-2与Hybrid的潜在类别占比进行了标注，而ML(-L)由于前文提到的βSDE符号问题此处不再研究.

ML中ML(N)、ML(RN)、ML(T)计算结果较为接近：VOWT约5.2元/min，VOIT约2.24元/min，均略高于MNL求解结果.ML(OT)的VOWT和VOIT分别为6.0元/min和2.55元/min，略高于前述3种ML模型.LCL-2和Hybrid在各潜类别的VOWT之间呈现出较为明显的层级化分，表明潜在类别分组与旅客时间价值之间可能存在关联性.Hybrid中Class2和Class4分别描述了两个具有ACMA属性处理规则的旅客群体；部分旅客的VOWT表现出的极大或极小值，使得中位数与总均值之间差异较大，呈现较强的偏态特征；而其VOIT的中位数与均值较为接近，表现出较强的对称性.此外，LCL-2的VOWT中位数与MNL计算结果接近，Hybrid的VOWT总均值结果大于其他模型，且LCL-2和Hybrid的VOIT中位数和总均值均小于其他模型.

4 结 论

本文以成都东客站出发旅客衔接方式选择的SP数据为依托，对MNL模型、不同连续分布假设的若干ML模型，以及离散分布假设的LCL和Hybrid模型进行了参数估计，采用支付意愿法从旅客个体和样本总体两个方面对异构模型的等候时间价值和车内时间价值结果进行了比较.结果表明，异构模型求解时间价值间存在较大差异，具体结论如下：

(1)参数分布假设对ML模型的时间价值结果具有较大影响.综合考虑时间价值CDF曲线和模型拟合效果，基于单侧三角分布的ML求解结果较为理想.

(2)离散分布模型中推荐使用能同时表达旅客属性偏好和处理异质性的新型Hybrid模型.但Hybrid在时间价值计算结果上可能表现出较为明显的偏态性，给样本总体的描述统计带来一定困难.

(3)MNL、ML、LCL和Hybrid模型在时间价值异质性表述上各有特点，目前尚无明确的比选方法.需要单独使用时间价值时可考虑取异构模型计算结果的均值.

本文时间价值测算源于SP数据环境，需要注意可能存在的主观特性.利用大数据环境下的RP数据展开模型分析将是论文下一步的研究内容.