基于振动信号盲源分离的船用空压机故障诊断

邵梦麟，员钦升，王 丽，杨文强，吴诗谦

（1. 中国船舶重工集团公司第七一一研究所，上海 201108；2. 海军工程大学 武汉 430033）

0 引言

船用往复式空压机主要用于为船舶主机和发电机提供起动能源，是船舶辅机系统的重要组成设备之一，具有运动部件多、结构复杂、噪音大、工作环境恶劣的特点，且由于一般运转在连续满载荷工况下，零部件较容易出现故障，一旦故障发生，将会对整船的正常运转产生不同程度的影响。通常情况下，选择在机体表面对空压机进行振动测试诊断，但是由于存在激励源众多、信号传递路径复杂、各运动部件产生的信号相互叠加干扰等现象，导致往复式空压机表面的振动信号频率分布范围广，且具有非线性和非平稳性的特点，给空压机振动信号的采集、提取、故障分析和测试诊断带来许多困难。

现有的信号分析系统通常使用快速傅里叶变换（Fast Fourier Transform，FFT）和自带的滤波方式对振动信号进行处理，但考虑到船用往复式空压机自身的结构组成和工作特点，仅利用上述方法，将难以去除背景噪声并判断其激励源。独立分量分析（Independent Component Analysis，ICA）和经验模态分解（Empirical Mode Decomposition，EMD）技术被广泛运用于旋转机械（尤其是航空发动机）上，但在往复式机械上运用较少。基于ICA优化算法进行盲源分离具有迭代次数少、计算复杂度低、稳定等优点，而且复原源信号很有效[1]，但是需要满足观测信号数大于等于源信号数这一假设条件。EMD算法将振动信号的时域图分解成一组本征模函数（Intrinsic Mode Function，IMF），对于非线性、非稳态信号分析具有很好的适应性，但是其求本征模态函数时并非用的数据局部平均值，不能确保IMF分量完成正交，即在处理后可能仍然有信号混叠，不能保证分离出来的振动激励源独立[2]。本文结合EMD和ICA算法[3]，利用 EMD算法处理单个观测信号，再利用 ICA分离，可以得到降噪性更好的振动信号，让故障定位准确性提高，从而解决复杂往复式机械在特殊环境下的故障诊断问题。

1 独立分量分析原理及数据验证

1.1 独立分量分析流程和算法选用

独立分量分析的根本目的是求矩阵W，满足U(n)=WX(n)相互独立，即U(n)为源信号S(n)的估计，其中X(n)是待分析信号，n为观测点数。为简化独立分量分析计算，需将数据进行预处理，分为两步，分别为去均值和白化。去均值也称为中心化，即将待分析信号X变成为0均值信号向量，令X=X－E[X]，式中E[.]为均值；白化是将待分析信号通过其协方差矩阵的特征分解进行线性变换，使得白化处理后的信号X~为单位方差、互不相关的信号，即满足式式中：I为单位矩阵。

首先建立ICA算法模型的目标函数L(X;W)，为

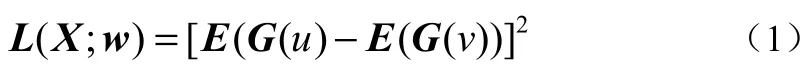
式中：wi为分离矩阵W的第i行；u为白化数据，u=wiX；v为0均值、单位方差的高斯随机变量。

再选用快速定点算法[4-5]作为化算法，该算法由Hyvarinen提出，具有快速、稳定、高效的优点，实际上是将N个源信号的独立分量分析问题变成了N个优化问题，即L(X;w)变为L(wi)(i=1,2,…,N)。定点算法步骤如下：

为防止wi向同一个值收敛，必须保证ui都互不相关，且提取第l+1个分量时必须满足wl+1与wl正交。其中非二次函数G(u)分为3种，如式（2）～式（4）所示。式（2）适用于超高斯与亚高斯源并存的情况。式（3）适用于峭度较大的超高斯信号的情况。式（4）适用于亚高斯源的情况。

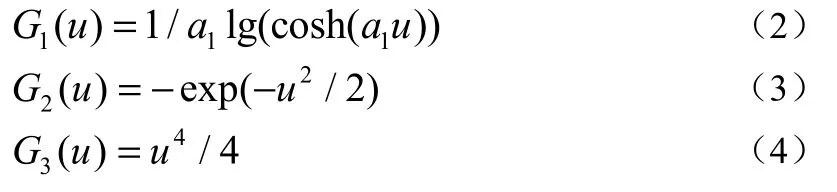
1.2 独立分量分析数据验证

为了验证所选用ICA优化算法的可用性，设置各种已知信号进行论证。分别设置正弦波、矩形波、锯齿波和随机信号共 4种已知源信号进行验证，采样点数均为500，且这4种信号相互统计独立，源信号波形如图1所示。

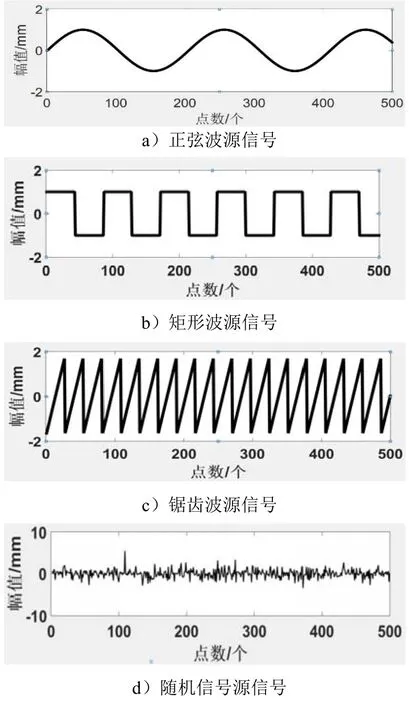
图1 源信号波形

根据盲源分离原理，对源信号进行处理，得到观测信号X(500)。X(500)是由源信号S(500)以式（5）的方式混合而成的。

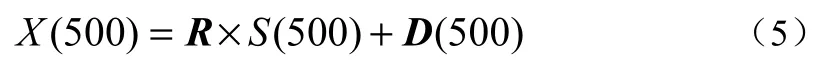
式中：R为随机正态分布的混叠矩阵，如式（6）；D(500)为噪声向量，。

本文噪声向量提取自船用往复式空压机正常运行时的测试数据，提取出工作状况下 4条明显的噪声信号，分离出来形成噪声向量，按比例减小了幅值，得到式（5）中D(500)，具体信号如图2所示。按上式混合后的信号如图3所示。

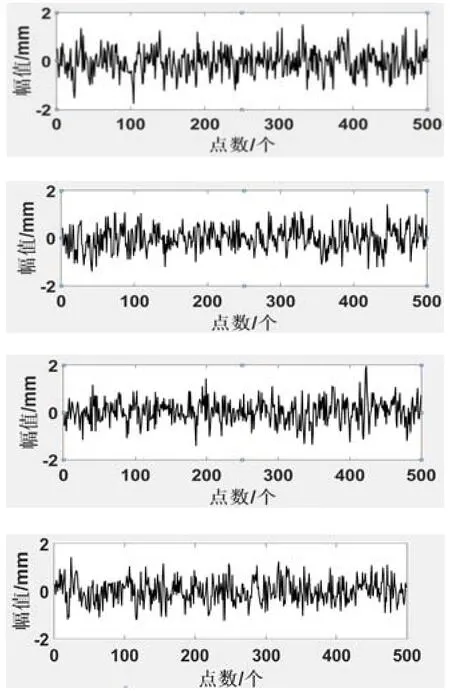
图2 噪声信号

图3 混合信号

采用对大峭度信号适应性好的G2(u)函数对混合信号进行分离，分离后的信号向量记为Y1、Y2、Y3、Y4，分离结果如图4所示。

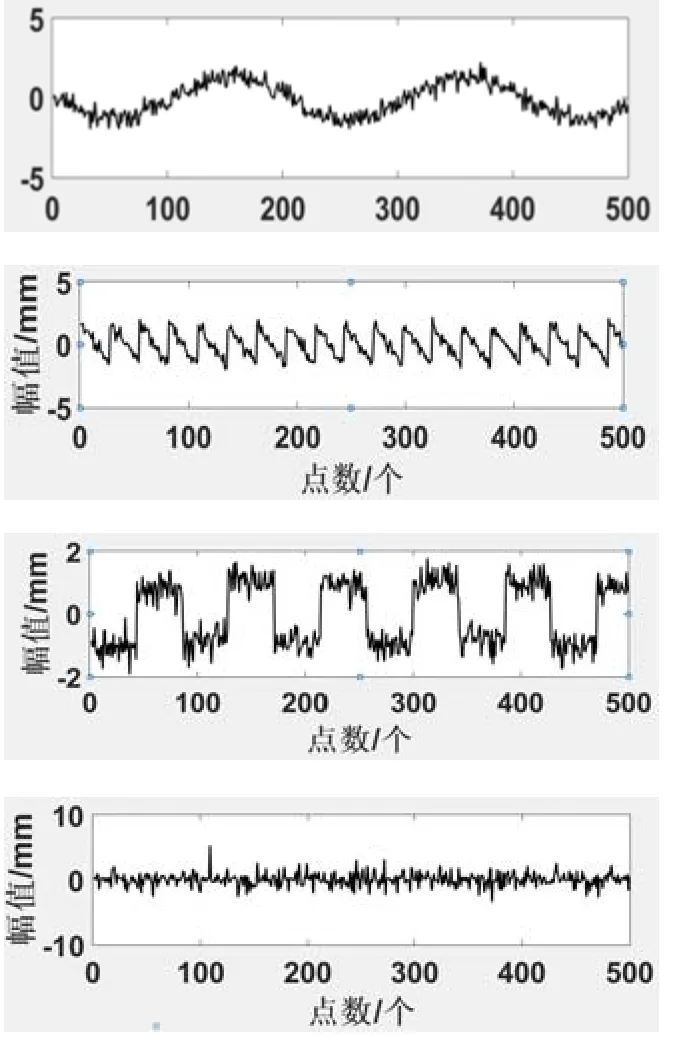
图4 ICA处理后信号

为了检验ICA优化算法对往复式机械噪声处理后效果，将图 1中源信号和图 4中估计源信号进行相关性分析，结果如表1所示。

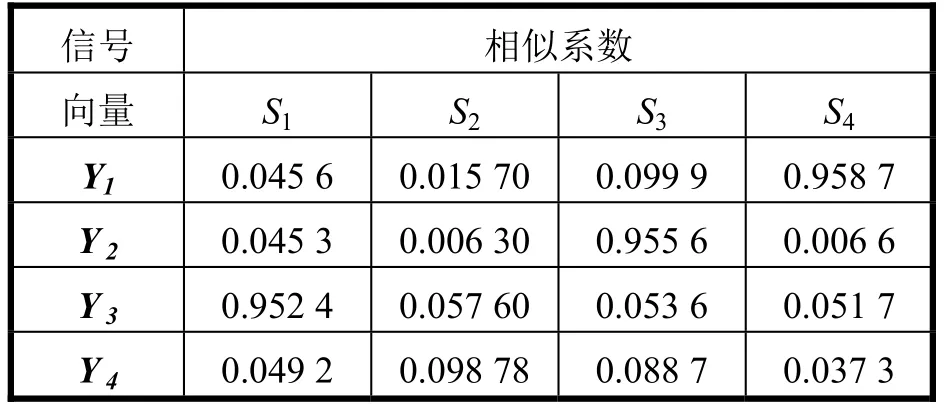
表1 源信号与分离信号的相似系数

取其中相似系数最大值[6]，分析可得：估计源信号与源信号相似度高于95%，选用的ICA优化算法可以运用于工程实际中。

2 空压机检修前振动测试与分析

2.1 待检修空压机性能参数与振动测点布置

由于船用往复式空压机工作环境恶劣，且船舱空间狭小，通常选择在空压机机体表面布置振动测试的测点。现以某船用V型、四级电动、双作用往复式空压机为对象，对其展开振动测试研究。该空压机电压为320 V时转速为1450 r/min，电压为280 V时转速为1330 r/min，电压为220 V时转速为1 150 r/min，需要功率（转速为1 330 r/min时）不大于75 kW，旋转方向从电动机方向看是顺时针。该空压机在运转过程中存在振感强烈、噪声过大且尖锐刺耳的问题，需通过对该空压机进行振动测试分析，定位故障源，为出现的上述问题提供维修技术方案。

测试所用仪器为东华 DH5901动态信号分析仪和DH186压电加速度传感器。采样参数设置为线性平均，平均次数4次，采样频率2.56 kHz，连续采样。按照振动测试标准规定[7-8]，每1个测点需测量3个相互垂直的方向，即与机器安装面垂直的方向（垂向），用Z标记；沿机器轴线的方向（纵向），用X标记；垂直XZ平面的方向（横向），用Y标记。测点布置位置为：自由端机脚（测点1）、自由端机体上部（测点2）、中部机脚（测点3）、输出端机脚（测点4）、输出端机体上部（测点5）、自由端机脚对称侧（测点6）。隔振器简化为弹簧，振级落差测试点布置位置为：空压机机体底部自由端（测点 7）与输出端（测点 8），这 2点垂直向下对应的船体上点分别为测点9和测点10。具体测点布置如图5所示。

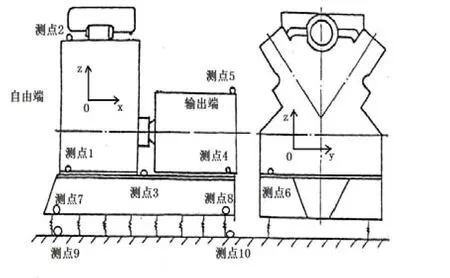
图5 空压机测点布置示意图

2.2 检修前空压机振动数据分析

空压机的整机振动烈度整理数据如表 2所示。通过表2数据和《往复式机器整机振动测量与评级方法》对比可知：该空气空压机的振动烈度值为10.92 mm/s，振动等级处于 A/B级临界边缘。为确定振动烈度的过大是否与隔振器有关，对隔振器数据进行处理，隔振器的振级落差处理数据如表3所示。

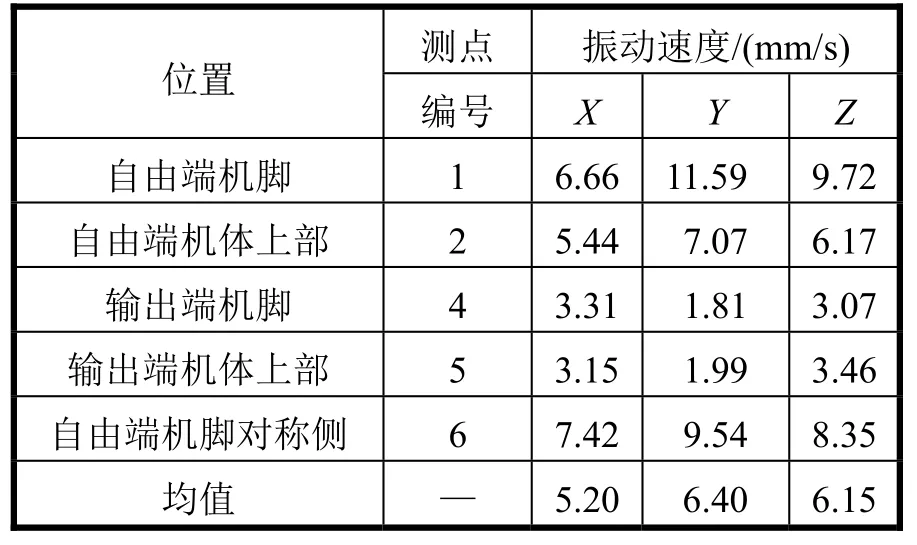
表2 空压机振动烈度测试结果

表3 空压机隔振器实验记录及评价表

由表 3可知：隔振器工作正常，能够成功起到减少空压机振动传递到船体的作用。因此，振感过大是由于空压机自身运行时振动过大，原因可以分为惯性力、气体力和机械冲击 3个方面。为进一步提取振动的特征数据以找到故障根源，对各测点 3个方向的时域波形进行研究，下面以自由端机脚X方向时域波形为例进行分析，利用传统方法仅做平滑处理的波形如图6所示。

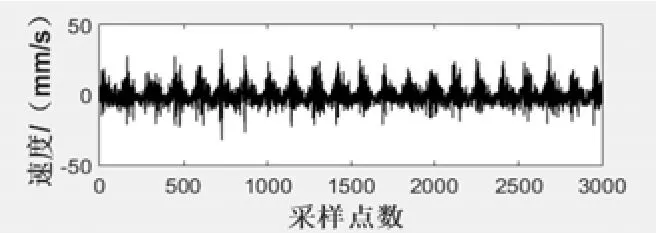
图6 空压机自由端X方向时域波形

2.3 利用 EMD和 ICA结合的方法对测试信号进行盲源分离

对采集到的信号进行预处理，然后进行经验模态分解，结果如图 7所示，通过观察结果可以发现：空压机振动信号通过EMD分解后得到的IMF分量具有一定的周期特性，IMF阶数与对应分量的中心频率和能量成负相关，与特征时间尺度成正相关。分量IMF1和IMF2的幅值最大，波形特征与测试所得信号相似，有显著局部冲击特性和非平稳的周期特性[9]。观察时域波形和波峰可知：2个冲击之间时间间隔为0.11 s，测试中空压机转速在1 100 r/min上下浮动，测试频率为2.56 kHz，由这些信息可以推算出对应的频率，如式（7）所示。

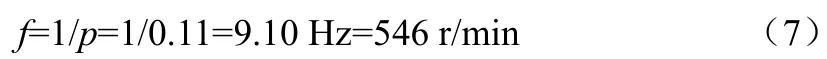
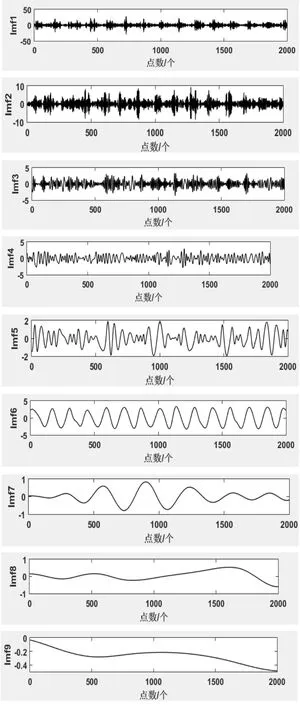
图7 EMD分解结果

这说明冲击的频率为 0.5×r/min，且冲击明显。这种情况可能由以下2种原因导致：1）当活塞磨损时，活塞和缸套间存在间隙，导致活塞在缸套中的往复运动产生摇摆，从而对缸套形成撞击，撞击为瞬时突加载荷；2）连杆小头磨损严重时，产生的间隙过大会导致往复运动时发生机械冲击。这两种情况下，振动信号的时域波形中可以发现冲击成分，且一般会激起气缸-活塞系统或者连杆-活塞系统的固有频率振动[10]。

由于往复式机械激励源众多、环境噪声强烈，加上 EMD算法本身分解时有可能产生模态混叠，同一IMF分量有可能存在多个噪声源，所以根据相关性准则对 9个分量进行相关性分析。得到相关系数依次为0.857 7、0.301 2、0.075 0、0.078 9、0.107 1、0.314 9、0.000 18、0.003 7、0.005 0。可以得到 IMF1、IMF2、IMF4、IMF5相关性较好，所以可以使用这4个分量建立4通道，利用ICA算法进行盲源分离，得到比较突出的故障频率、噪声以及其他传动部件的频率，其频谱如图8所示。

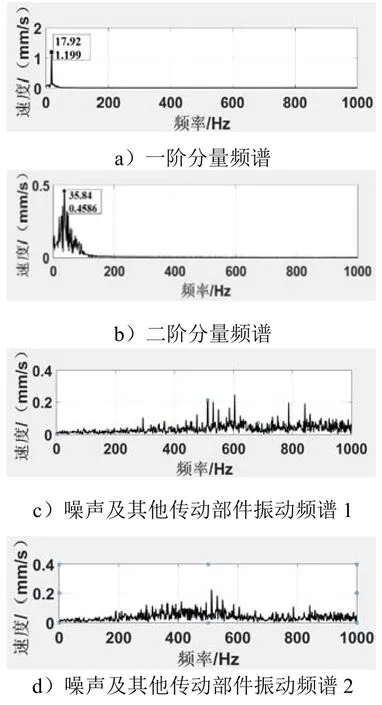
图8 ICA进行盲源分离结果

图8a）中，频率17.92 Hz比较突出，可知是1×r/min频率；图8b）中，35.84 Hz频率比较突出。综合其他测试部位和测点可知，整机中X、Y向均伴有2×r/min频率。

根据往复式压缩机运动机理，假定往复部件的总质量为ms（包括活塞组件、十字头和连杆小头部分的转化质量），计算得到往复运动的惯性力为

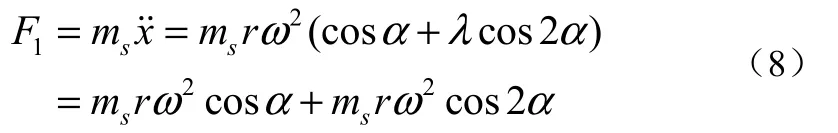
式中：α曲柄转角，α=ωt+φ。由式（8）可知往复惯性力由2部分组成：1）一阶往复惯性力，曲柄旋转一周的时间即为力的变化周期，因此曲柄的转动频率即为一阶往复惯性力引起的振动频率；2）二阶往复惯性力，曲轴旋转半周的时间即为力的变化周期，因此曲轴转动频率的二倍即为二阶惯性力引起的振动频率[11]。

该机在运行过程中曾出现过I、IV级气阀损坏、III级活塞脱落1次、IV级活塞脱落2次、IV级缸套拉缸等故障，对应上述不同故障现象进行了数次零配件更换与修理。所以，本次测试对该空压机的检修建议是进行平衡组件的检查和活塞部件的更换。

3 检修后数据整理与分析

通过拆检发现空压机活塞有磨损情况，将其更换。该空压机平衡主要依靠布置在曲轴箱两侧的 2个平衡机构部件，压缩机工作时，I级平衡铁转速等于曲轴转速，而 II级平衡铁转速为曲轴转速的两倍，分别起到平衡压缩机 I阶和 II阶往复力的作用。根据原理对平衡部件进行了重新平衡。检修完成后，对机器振动进行了第二次测试，振动烈度如表 4所示，振动烈度值为6.49 mm/s，振动等级为A级，结果表明振动烈度已经有显著减小并达到要求。

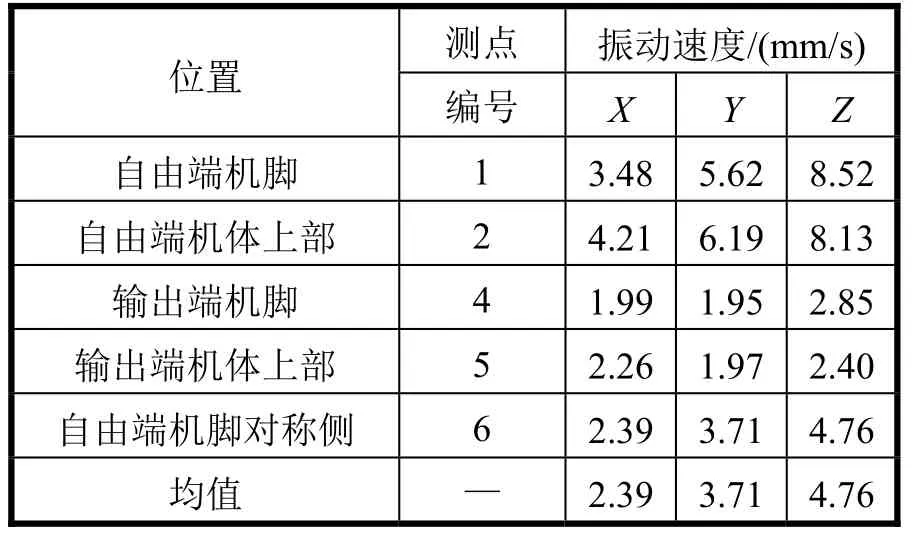
表4 空压机二次测试振动烈度测试结果

为了确定故障被排除，对各测点的时间波形再次进行分析。以自由端机脚测点为例，自由端机脚X方向修理后波形如图 9所示，由图 9可知：振动幅值大幅下降，冲击现象明显减缓。

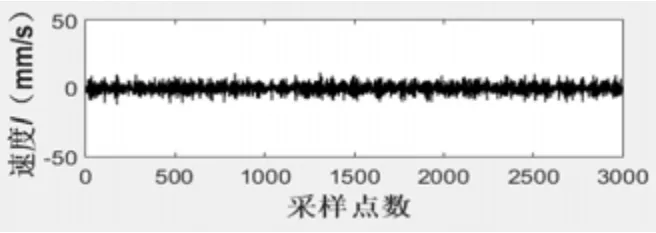
图9 空压机修理后自由端机脚时域波形

4 结论

ICA和 EMD算法对机械振动信号有很好的适用性，但是在往复式机械上，EMD和ICA的联合算法运用还较少。本文通过ICA优化算法的仿真和对实际信号的测试诊断，得到如下结论。

1）在ICA优化算法的仿真验证中，加入往复式机械的背景噪声信号向量，弥补了以往只对源信号进行矩阵变化而不添加噪声分离的缺陷。验证结果表明在有往复式机械背景噪声信号的干扰下，分离的相似度仍有95%，所选ICA算法可以运用到往复式的振动信号处理中。

2）实测的某船用空压机工作环境特殊，测试环境狭小且空压机周围布置紧凑，测试点数很难达到 ICA运行的前提要求，将EMD和ICA算法联合使用，对EMD的IMF分量进行剔除并构成虚拟通道能够解决这一问题。

3）对测试前后空压机振动幅值和信号谱线进行比较，发现故障已经排除，验证了检修方案的正确性。本文介绍的算法具有简单、高效的特点，在对船用往复式空压机的振动信号进行分析时，其可在一定程度上满足工程应用的需求。