几何画板（GSP）辅助高中数学圆锥曲线教学的实践研究——以吉林省前郭县第五中学为例

（前郭县第五中学，吉林前郭131100）

一、研究意义

教育部发布的《普通高中数学课程标准（2017年版）》指出“数学承载着思想和文化，是人类文明的重要组成部分，是自然科学的重要基础。”由此可见，数学不仅是一门科学，更是一种普遍运用的技术。从古至今，数学产生的作用都是不可估量的，它的地位也是不可代替的。

而作为高中数学选修（文）1-1，（理）2-1第二章重要模块的圆锥曲线，不管是在高考中还是在生活中，从不缺乏压轴的分量。圆锥曲线模块是各省、直辖市高考考察的重点内容，从高考数学学科占比来说，其中存在着考点较多的情况，这些考试所涉及的知识点覆盖了离心率、准线方程等诸多方面。笔者专门就2018年我国各地数学高考试卷中圆锥曲线问题考察情况进行统计分析（如表1）。

表1 2018年各省、直辖市高考试卷中圆锥曲线问题考察情况汇总表

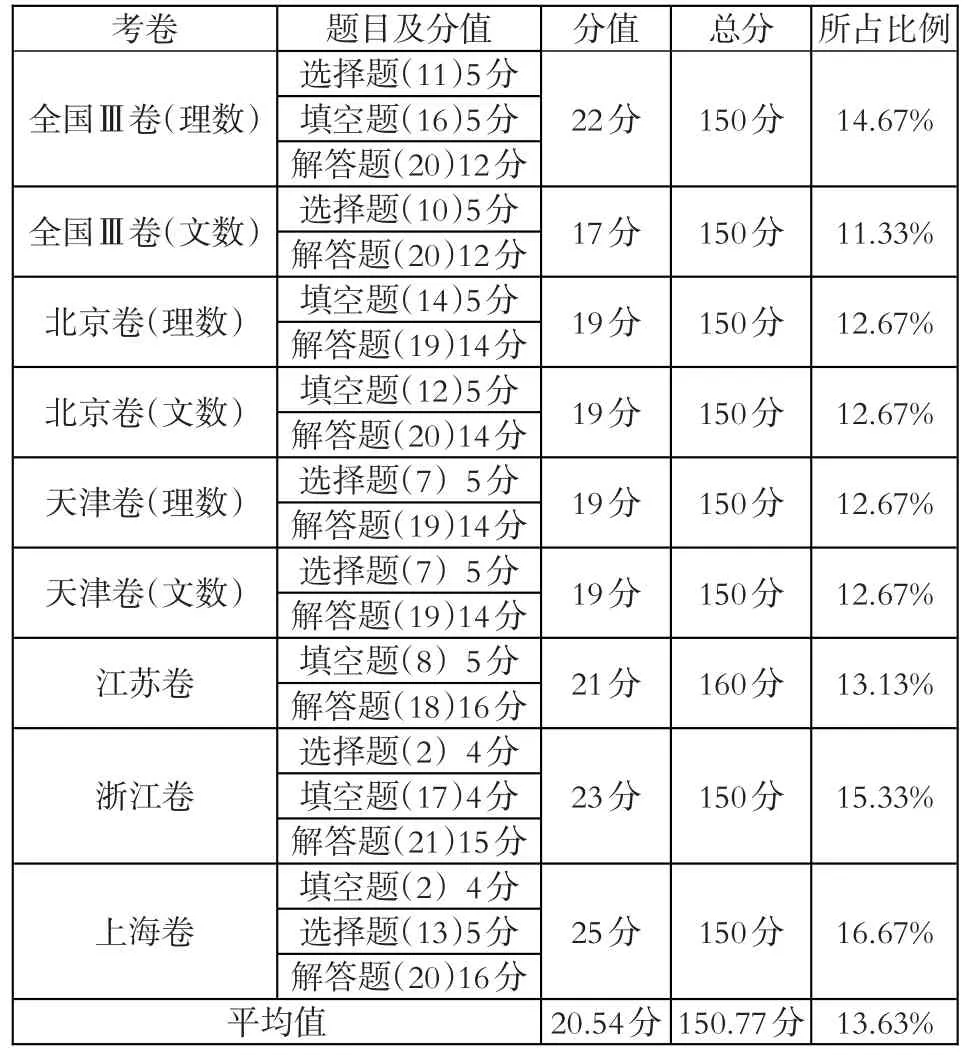
考卷全国Ⅲ卷（理数）分值22分总分150分所占比例14.67%全国Ⅲ卷（文数）17分150分11.33%北京卷（理数）北京卷（文数）天津卷（理数）天津卷（文数）19分19分19分19分150分150分150分150分12.67%12.67%12.67%12.67%江苏卷21分13.13%150分浙江卷15.33%上海卷题目及分值选择题（11）5分填空题（16）5分解答题（20）12分选择题（10）5分解答题（20）12分填空题（14）5分解答题（19）14分填空题（12）5分解答题（20）14分选择题（7）5分解答题（19）14分选择题（7）5分解答题（19）14分填空题（8）5分解答题（18）16分选择题（2）4分填空题（17）4分解答题（21）15分填空题（2）4分选择题（13）5分解答题（20）16分平均值25分20.54分23分160分150分150.77分16.67%13.63%

图1 2018年各省、直辖市高考数学试卷中圆锥曲线问题考察所占分值雷达图

从表1中可以清楚地看到，数学高考试卷中必定有一部分涉及圆锥曲线的考点，通常情况下都是以解答题形式出现。也有不少地区高考数学试卷中除解答题之外，还会附带一道选择题或是填空题，甚至还会出现该考点覆盖三种题型的情况。从图1中可以发现，在满分为150分的高考卷中（江苏为160分），涉及圆锥曲线的考点所占分值占较大比重，基本上在11%-16%区间，这也就意味着，一张150分的卷子中，圆锥曲线大概占17-25分。全国各省、直辖市的高考试卷中圆锥曲线考察平均分数达到了20.54分，所占比例为13.63%。

2017年，我国教育部在发布的《普通高中数学课程标准（2017年版）》中首次提出了数学区别于其它学科的核心素养具体为：一是数学抽象；二是逻辑推理；三是数学建模；四是直观想象；五是数学运算；六是数据分析。本次课标修订坚持结合时代要求并着力发展学生的核心素养。其中，“直观想象”作为高中课标修订组精心提炼的六大核心素养之一，主要表现为学生的数形结合能力，几何直观和空间想象能力。

有直观，可想象，正是几何画板软件自身的特点。几何画板软件的使用既可以达到为学生形象地展示动态几何问题的形成过程，也可以令学生体会到数与形相结合的数学美，最重要的是可以辅助学生系统地学习知识。

可见，研究此课题是教师教学、学生学习迫切需要的，同时，也推动了信息技术与数学学科融合的力度和进度，对数学教育改革中充分运用多媒体教学，及更有效地利用几何画板也有着重要的实际意义。

二、几何画板辅助圆锥曲线教学实践研究设计

（一）研究对象

研究对象选择吉林省松原市前郭县第五中学高二年级的任意四个平行班级。将其分为两个对照班和两个实验班，下文中我们分别标记为D班和S班。D班在接触圆锥曲线的新知识以及课堂练习中采用传统的教学模式，即数学教师使用静态的图片或板书引入课堂教学当中；S班授课时采用几何画板绘图软件，能够将圆锥曲线的构造过程动态的显示出来。我们通过考试测验以及问卷调查的方法对比对照班、实验班的学习效果。

（二）研究内容设计

吉林省松原市前郭县第五中学作为省级示范高中，该校引入几何画板的时间较早，在每个班级中均配备多媒体教学设备，学生对什么是几何画板已经具有一定的认识，且会简单操作及绘图。四个班级的授课教师均相同，时间跨度方面为两周，共计为70课时。其中选定D班作为对照班，并在该班级采用的是传统教学模式来进行教学，而S班则为实验班，在该班的教学则采用几何画板教学方式。

三、基于案例研究的教学效果对比分析

（一）利用定义解题的案例教学效果对比分析

在使用不同教学方法讲解利用圆锥曲线定义解题的方法后，给出了关于圆锥曲线用定义解题方面的考试试题，同时对D班和S班进行了分班级、排考场、拉单桌的专门模拟考试。结果显示，D班的很多学生圆锥曲线的测试卷成绩明显要低于S班学生的成绩。考试成绩在95分以下，D班人数明显多于S班，而95-115分、115-135分、135分以上的三个区间当中，D班人数明显分别少于S班人数（如图2）。

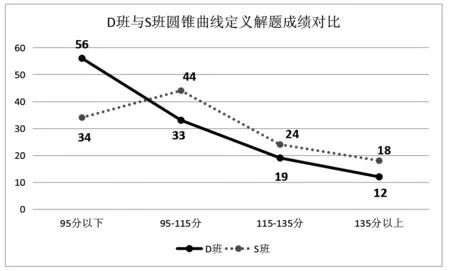
图2 D班与S班圆锥曲线定义解题成绩对比图

（二）求标准方程问题的案例教学效果对比分析

同理，在实施不同教学方法讲解求圆锥曲线标准方程问题后，给出了关于求圆锥曲线标准方程方面的考试试题，同时对D班和S班进行了分班级、排考场、拉单桌的专门模拟考试。结果显示，D班的很多学生圆锥曲线的测试卷成绩明显要低于S班学生的成绩。在95分以下，D班人数明显多于S班，而95-115分、115-135分、135分以上的三个区间当中，D班人数明显分别少于S班人数（如图3）。

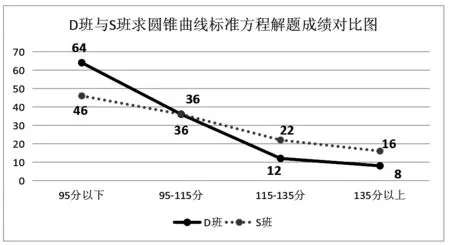
图3 D班与S班求圆锥曲线标准方程解题成绩对比图

（三）问卷调查数据结果分析

本次问卷调查共发放问卷248份，回收240份，其中，有效问卷240份，有效率达97.56%，其中，两个对照班级的学生共发放各124份调查问卷，两个实验班的学生共发放124份调查问卷。其中，收回D班有效问卷119份，S班有效问卷121份，两份调查问卷的有效度各为：95.97%、97.58%，均符合问卷调查的效度要求，所以，调查结果成立，以此为基础展开分析研究。

在研究对象的248人中挑选出有效问卷的240人，对其圆锥曲线相关测试进行学业成绩的排名，前27%即总排名前65人作为高分组，后27%即总排名后65人作为低分组。

1.不同学业成绩学生在两种教学模式上的差异分析

对于高中生在几何画板辅助教学模式和传统教学模式的使用上进行差异性检验。结果发现，在方差齐性的条件下，不同学业成绩的学生在几何画板辅助教学和传统教学的得分上存在显著性差异，进行事后检验，发现在选择几何画板辅助教学模式上，优等生高于困难生，在选择传统教学模式上困难生高于优等生（如表2）。

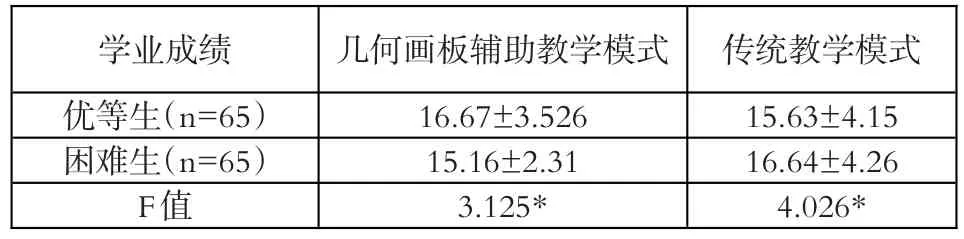
表2 不同学业成绩学生在几何画板教学和传统教学模式上的差异结果（M+SD）

2.两种教学模式与学业成绩之间的相关分析

本研究对几何画板辅助圆锥曲线教学和传统圆锥曲线教学模式对学业成绩的影响进行了相关分析。由表3可知，几何画板辅助圆锥曲线教学与学业成绩的高低之间存在显著的正相关。说明，几何画板的使用越多越主动，学习成绩就会越高；反之，不主动使用几何画板，也就不会取得好的学业成绩（如表3）。

表3 几何画板辅助教学和传统教学模式与学业成绩的相关结果（n=240）

四、结论与建议

将几何画板（GSP）引入高中数学圆锥曲线的教学对提高学生学习效果是有一定作用的。

（一）运用GSP可以提高圆锥曲线课堂教学效率

几何画板作为备受认可的重要教学工具，在数学教学中引入该工具之后能把过去较难解释清楚的圆锥曲线等数学概念直观地展示出来，能使得学生对该知识更加容易理解，进而促使课堂教学效果实现有效提升。

在S班进行课堂教学时，学生均非常积极，学习兴趣也极为浓厚，非常乐于和教师等进行互动。在D班开展教学活动时，尽管学生也都非常认真，不过整个课堂较为沉闷，基本上教师问什么，学生就答什么，在主动性方面较为薄弱，学习兴趣也无法和S班相比拟。综合来说，在实验班S班开展的课堂教学效果更为理想，相比之下对照班D班的课题教学效果则要差一些。

（二）利用GSP创设情境更能激发学生的求知欲

在D班开展课堂教学活动时，涉及新知导入这部分的教学采用了PPT图片静态展示方式，未能有效吸引学生注意力，使得学生对相应知识点的掌握并没有明确，甚至不了解这些内容知识。学生在思考时有的也直接提出测量方法，但由于PPT未有互动性，加上授课时间本身就有限，这就很难激发学生的学习积极性。

教师在S班开展课堂教学活动时，涉及新知导入这部分内容就可借助几何画板的动态演示功能进行展示，能抓住学生关注点，这在奥苏贝尔提出的学习动机理论也有相应阐述，能有效激活学生学习积极性。之后教师就可以把构成圆锥曲线的图形进行分离，并引导学生进行思考，学生据此就能初步发现圆锥曲线中有关焦点、定点、焦距等的相关规律。三种圆锥曲线椭圆、双曲线、抛物线因为其构成的不同其图像规律等也有很大的差别。

综合以上分析可以得知，几何画板在激发学生学习兴趣与激活其学习欲望方面的效果非常明显，进而促使教学质量也获得相应提升。

（三）GSP可提高学生独立思考和动手实践能力

在D班教师也给学生进行独立思考的机会，且还安排其进行自主探究，然而在作图过程中很难避免不出现偏差，这与数学这门学科具有严谨性特点不符合，即在对相应问题进行说明时，需要借助精准的图形来进行说明。从学生这个层面上而言，其存在这种误差猜想自然无法获得有效验证，这对提升其学习质量非常不利，这种情况下进行的独立思考自然无法获得相应效果。

而在S班则不同，教师先是结合学生实际并给其进行自主探究以及独立思考的机会，学生在这个过程中则借助几何画板来进行精确作图，当存在疑惑时，可在教师的引导下解决这些问题，使得其独立思考能力获得提升。由此能说明的是，在数学课堂中利用几何画板这个工具，能有助于培养学生独立思考以及动手实践的能力。

（四）GSP辅助教学有助于学生数学核心素养的培养

几何画板给学习困难的学生带来极大帮助，能为其提供进行反复学习的重要机会。而借助几何画板制作出来的文件非常小，便于学习者携带。当学生需要反复认识相应的概念时，就可以把文件复制回家，之后在家里进行反复学习，据此来达到掌握这些知识的目的。此外，这还能促进学生“数学抽象”以及“逻辑推理”能力的培养。

而且新课标中提到的“直观想象”作为高中课标修订组精心提炼的六大核心素养之一，主要表现为学生的数形结合能力，几何直观和空间想象能力。有直观、可想象正是几何画板软件自身的特点。几何画板软件的使用既可以达到为学生形象地展示动态几何问题的形成过程，而且可以令学生体会到数与形相结合的数学美，最重要的是可以辅助学生系统地学习知识。