基于VSG的光伏发电系统建模与仿真研究
2018-12-28樊然然唐文星
孟 超,赵 咪,樊然然,唐文星
(石河子大学机械电气工程学院,新疆 石河子 832000)
0 引言
近年来,随着环境污染和化石能源短缺等问题的日益严重,新能源的利用已成为人们关注的焦点[1]。其中,光伏发电以其清洁、经济等优点,得到了大力发展[2]。光伏并网发电具有很大的随机性和波动性,会造成电压幅值和频率的严重波动,影响电网的稳定运行[3]。光伏并网采用电力电子逆变器接口,导致系统中的旋转惯量减少,系统缺乏惯性、阻尼等特性,耐冲击能力差。因此,当系统负荷波动或内部出现故障时,会造成系统频率失稳和内部不稳定。在此背景下,如何通过控制变流器以实现光伏发电高效、友好的并网,是亟待解决的关键问题[4]。
同步发电机具有对电网天然友好的优势,若借鉴传统电力系统运行经验,使并网逆变器具有类似同步发电机的特点,则可实现光伏发电的友好接入,并提高发电系统的稳定性[5]。为此,虚拟同步发电机(virtual synchronous generator,VSG)技术应运而生[6],改善了逆变器的并网特性,向电网提供了必要的频率和电压支撑。其中,文献[7] 研究了VSG控制对改善微电网频率稳定性的作用,但未详细介绍底层矢量并网控制算法。文献[8] 设计了在负荷扰动条件下,自动改变惯性系数以消除功率波动的方案,但功率的波动幅值依然很大。
鉴于此,本文针对光伏发电系统,提出了一种电压型VSG控制策略。首先,阐述了目前常用的两种VSG类型及其原理;并分析了VSG的有功频率控制和无功电压控制原理,建立电压型VSG的二阶数学模型。然后,利用MATLAB/Simulink,搭建了基于VSG的光伏发电系统模型。最后,对光伏阵列的输出特性、VSG控制策略和光伏发电系统的运行特性进行了仿真试验。
1 VSG控制方法
1.1 VSG类型
现有VSG技术主要包括两种技术路线。一种由鲁汶大学和克劳斯塔尔工业大学提出,通过控制逆变器输出电流dq轴分量,使新能源发电设备具备调频调压功能的电流控制型VSG,可以等效为一个电流源[9],难以为系统提供电压和频率支撑。另一种由利物浦大学等机构提出,通过控制逆变器内电势的幅值和相角,使新能源发电设备具备调频调压功能的电压控制型VSG[10],实现了VSG和同步发电机在物理和数学模型上的较好等效,并可实现VSG无锁相环的自同步运行,能较好地提升母线电压稳定性。本文选用电压控制型VSG实现光伏发电系统的仿真分析。
1.2 VSG的本体算法
根据不同阶次的同步发电机模型,可建立不同的VSG数学模型。在众多模型中,二阶模型可以完全消除同步发电机复杂的电磁耦合关系,进而实现对输出功率的良好控制。经典二阶同步发电机等值模型如图1所示。
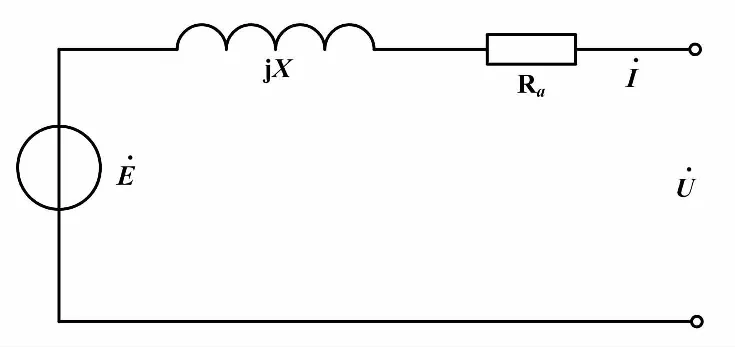
图1 经典二阶同步发电机等值模型
从图1可得同步发电机的二阶机电暂态模型[11],如式(1)所示。
(1)
式中:E为VSG的感应电动势;I、Ra和U分别为电枢电流、电枢电阻和电枢电压;X为同步电抗;θ为功角;Tm和Te分别为机械转矩和电磁转矩;D为阻尼转矩系数;Δω为额定角频率与实际角频率之差;Pm和Pe为机械功率和电磁功率;ω为额定角频率;J为转动惯量。
1.3 有功频率控制
频率是衡量电能质量的一个重要指标,因此控制系统的频率在允许的范围内波动,是保证电力系统稳定运行的一项基本任务。VSG的有功频率控制实际上是模拟同步发电机的调速器来表征有功功率和系统频率的下垂特性,使得系统的有功功率保持平衡。其控制方程如式(2)所示。
(2)
式中:P0为VSG的有功功率参考值;ω0为角速度参考值;R为下垂系数;Pe为额定有功功率。
根据式(2)可得虚拟同步发电机的有功频率控制原理框图,如图2所示。
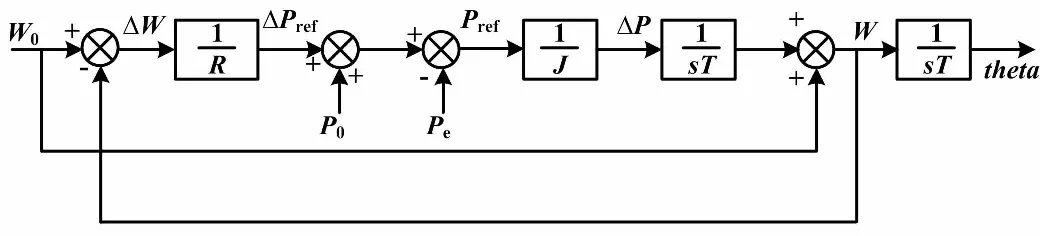
图2 有功频率控制原理框图
从图2可知,当调速器动作时,将设置的角速度参考值与系统的额定角速度进行比较,所得的角速度差值乘以调差系数后转化为系统缺少的有功功率,再与有功功率参考值和额定有功功率作简单运算,即可得有功功率差ΔP。调速器通过检测ΔP来控制虚拟机械转矩输出,从而调节频率。
1.4 无功电压控制
电力系统中,电压过高或过低都将对人身和用电设备产生重大影响。因此,保证用户的电压接近额定值是电力系统的另一项基本任务。VSG的无功电压控制实际上是模拟同步发电机的励磁控制器来实现无功功率和电压幅值的下垂特性,使得系统的无功功率保持平衡。其控制方程如式(3)所示。
Emag=U0+K(Qn-Qe)
(3)
式中:Emag和U0分别为VSG的输出电压和参考电压;K为调差系数;Qn和Qe分别为VSG的无功功率参考值和输出的无功功率。
虚拟同步发电机的无功功率电压控制原理如图3所示。
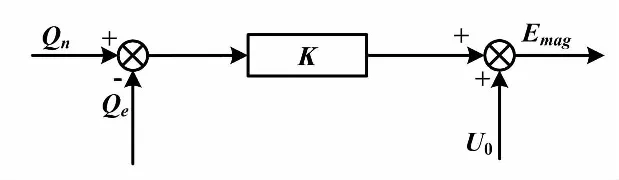
图3 无功功率电压控制原理框图
通过测量得到系统某时刻的无功功率,并与设置的无功功率参考值进行比较,即可求出一个无功功率差。其差值乘以调差系数K后,可得系统的电压差额。该差额与电压参考值进行求和后,可得调整电压。
2 基于VSG的光伏发电系统仿真分析
2.1 基于VSG的光伏发电系统
基于VSG的光伏发电系统主要包括:光伏阵列、BOOST电路、最大功率跟踪(maximum power point tracking,MPPT)、脉冲宽度调制(pulse width modulation,PWM)、调速器、励磁控制器、VSG算法、正弦脉冲宽度调制(sinusoidal pulse width modulation,SPWM)、滤波电路和负载等模块。基于VSG的光伏发电系统结构如图4所示。
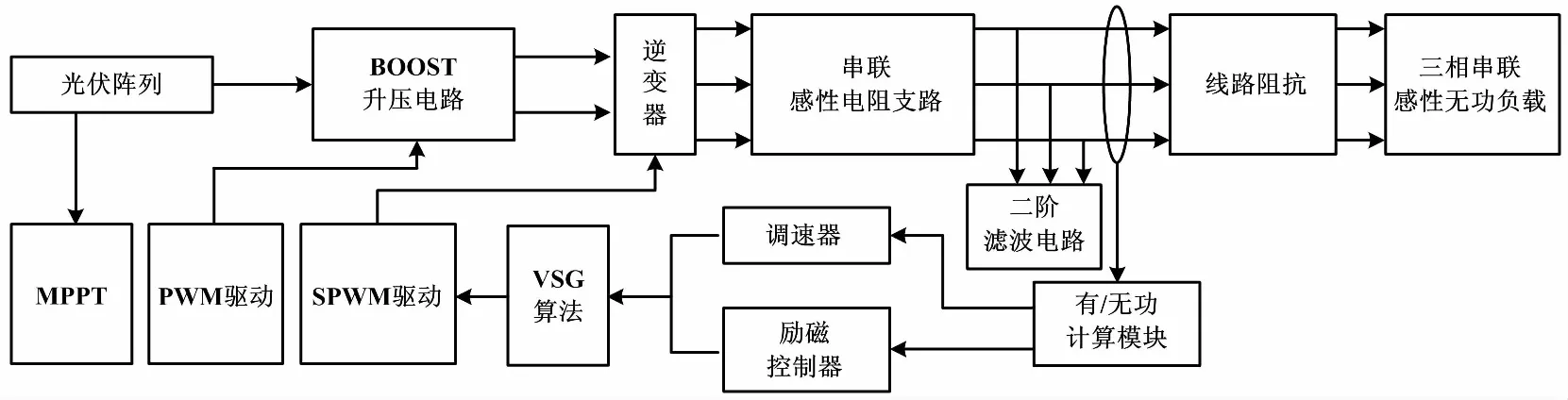
图4 基于VSG的光伏发电系统结构图
为了验证控制算法的有效性,基于MATLAB/Simulink仿真平台搭建系统仿真模型。仿真参数为:Isc=59.8 A;Im=55.6 A;Uoc=438 V;Um=360 V;直流侧逆变电压为766.5 V;额定频率为50 Hz;滤波电感为8 mH;滤波电容为40 μF。
2.2 光伏阵列输出特性分析
光伏阵列的输出特性随一天内的环境温度(T)和光照强度(S)的变化,按照一定的规律变化[12]。
设T为25 ℃恒定不变,而S分别为1 000 W/m2、750 W/m2和500 W/m2。则当S等差减小时,光伏阵列输出I-U和P-U特性曲线如图5所示。
从图5的仿真结果可知:①光伏阵列的Isc与S成正比关系,S每增加250 W/m2则Isc约增加1 A,S对开路电压Uoc的影响不大;②电池的输出功率P与S成正比关系,S对P的影响显著,尤其是功率峰值点处。
设S为1 000 W/m2恒定不变,而T分别为15 ℃、25 ℃和35 ℃。则当T等差增加时,光伏阵列输出I-U和P-U特性曲线如图6所示。
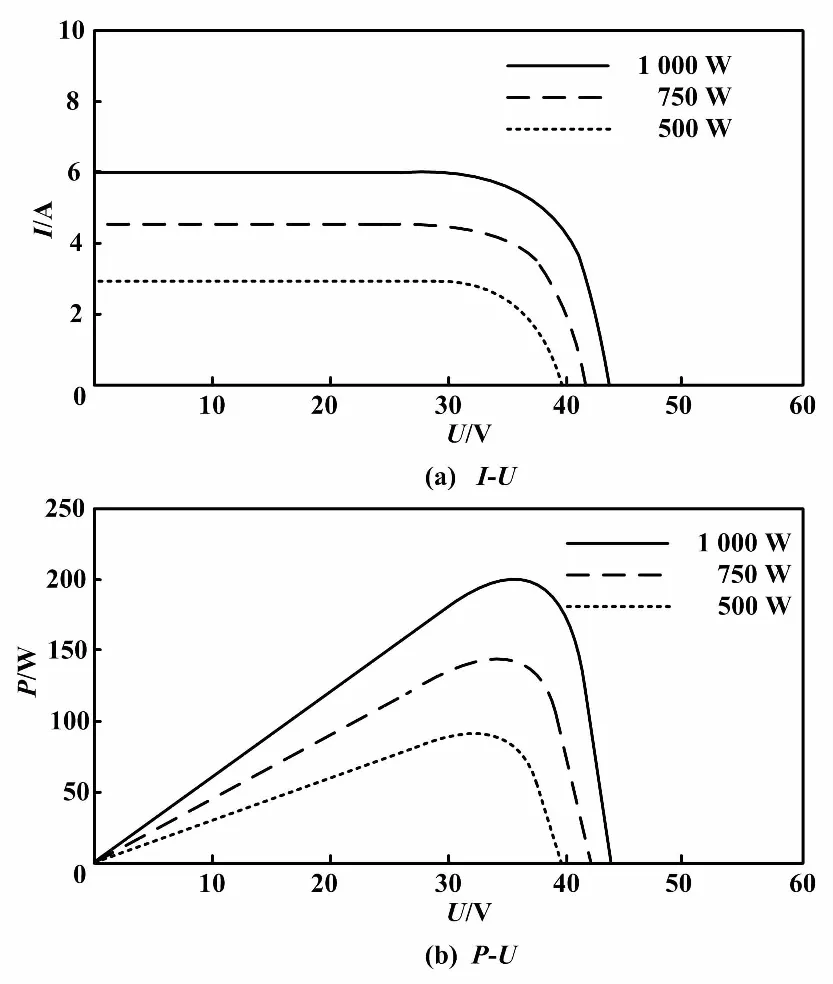
图5 光伏阵列输出特性曲线(S等差减小)
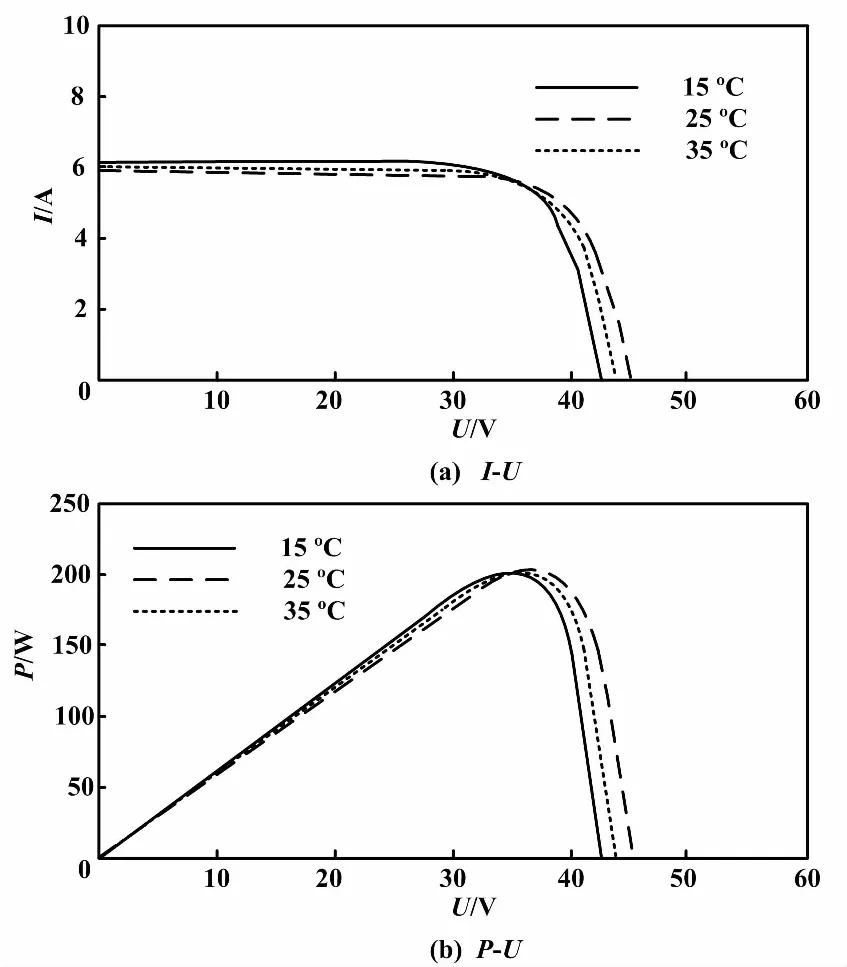
图6 光伏阵列输出特性曲线(T等差增加)
从图6的仿真结果可知:①光伏阵列的Uoc与T成反比,T每升高1 ℃则Uoc约下降2~2.3 mV,Isc与T成正比关系,但T对Isc的影响不明显;②电池的输出功率P与T成反比关系,T每升高1 ℃,P损失0.35%~0.45%。
综上所述,T对电压影响很大,S对电流影响很大。随T和S的改变,光伏阵列的输出特性成非线性关系变化,其最大功率点(maximum power point,MPP)也是随时变化的。当条件改变时,每条功率特性曲线都有唯一的MPP与之对应。
2.3 光伏发电系统运行特性分析
保持T为25 ℃恒定不变,初设S为1 000 W/m2,在0.5 s时升为1 500 W/m2,0.7 s时降为500 W/m2。利用电导增量法MPPT控制算法,得到的光伏阵列仿真波形如图7所示。仿真结果表明:当S改变时,光伏阵列输出电压基本不变,输出电流变化较明显且与S成正比变化,与光伏阵列的输出特性规律相一致。光伏阵列输出功率在最大功率处无规律波动,在系统运行时始终工作在最大功率跟踪状态,使系统输出功率最大,有效提高了光伏发电系统的利用率,由此证明了VSG控制策略的有效性。
初始时刻系统带额定负荷,有功功率5 400 W,无功功率3 200 Var,在0.33 s时有功功率负荷增加940 W,0.5 s时有功功率减少2 270 W,0.667 s后有功功率又增加1 330~5 400 W,整个过程中无功功率保持不变,系统的仿真波形如图8所示。
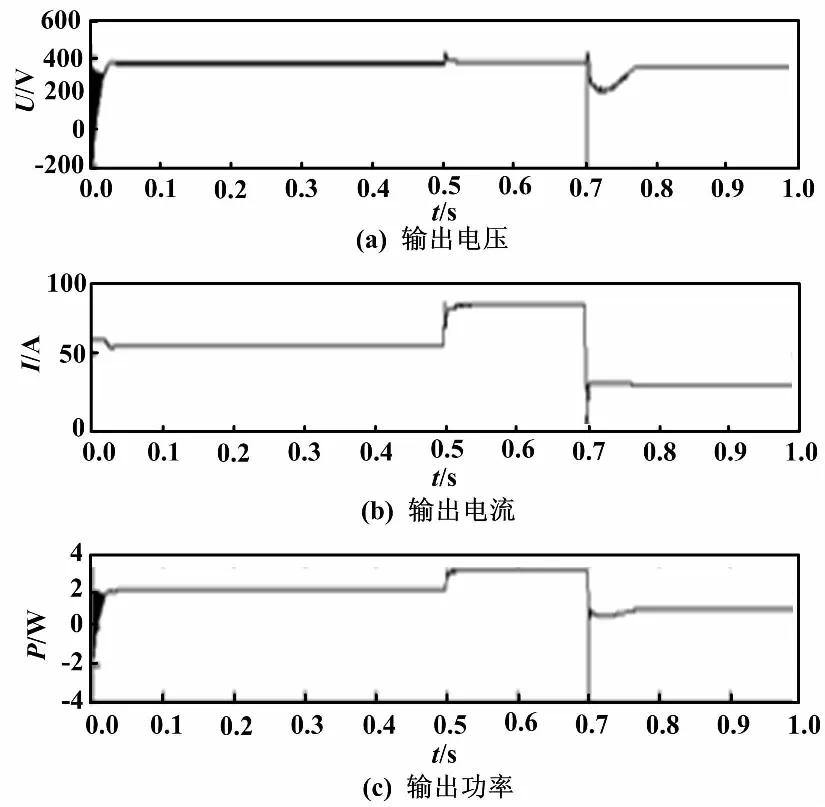
图7 仿真波形(光照强度变化)
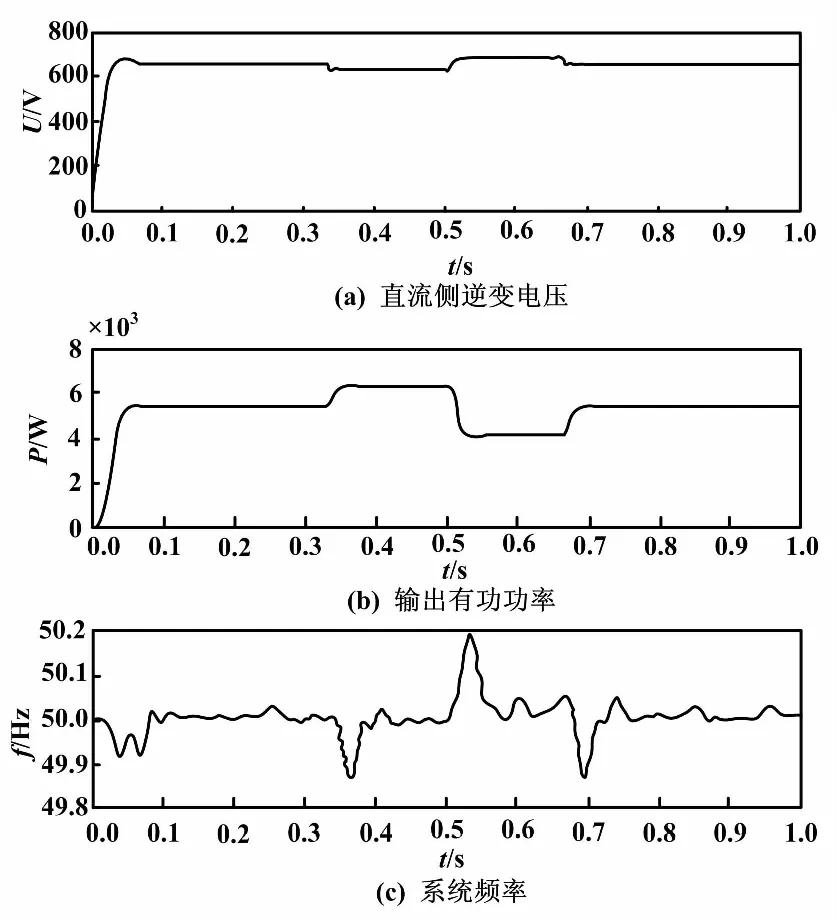
图8 仿真波形(无功功率保持不变)
从图8可知,光伏发电系统较容易受到负荷变化等因素干扰,出现运行波动的情况,波动的激烈程度取决于负荷变化大小等多种因素的影响。VSG控制策略能保证直流侧逆变电压和VSG输出有功功率快速响应负荷变化,维持系统功率平衡,频率稳定。直流侧电压和系统频率与负荷成相反趋势变化,体现VSG控制策略的下垂特性。
3 结束语
VSG具有同步发电机的外特性,对提高电网对光伏阵列发电的消纳能力、改善电网变流器接口特性具有重要意义。本文首先介绍了VSG的基本原理,然后建立有功频率控制和无功电压控制方法,最后利用MATLAB/Simulink搭建了光伏发电系统的整体仿真模型。试验验证了基于VSG的控制策略能根据系统负荷的波动而调整输出特性,自动维持系统功率平衡,具有很好的调频功能;同时,其控制结构简单,同步速度快,实用性强,有效提高了光伏发电系统的输出效率。
综上所述,VSG控制在光伏发电系统中极为重要,今后可考虑在VSG故障穿越和VSG并网小干扰稳定控制与暂态稳定控制等方面展开研究。
