T形钢管混凝土柱与H型钢梁节点性能研究
2018-12-28赵滇生严航洋
赵滇生,严航洋
(浙江工业大学建筑工程学院,浙江 杭州 310014 )
钢管混凝土结构已经在很多领域中有了广泛的应用,不仅具有承载能力高、韧性塑性好、耐火性能优良的特点,而且施工简便,节约人工费用,降低工程造价,经济效益好[1]。钢管混凝土异形柱,可有效避免房间棱角,而且截面尺寸也可以减小。
近年来,国内外专家学者的研究方向大多集中在圆钢管混凝土柱以及方钢管混凝土柱的节点上,而钢管混凝土异形柱的节点研究相对较少。我们运用有限元软件分析竖向加劲肋对T形钢管混凝土柱与H型钢梁的连接节点力学性能的影响。
1 有限元分析模型
1.1 节点尺寸
我们参考一栋钢结构建筑,节点上下柱的长度取1/2的柱高,节点左右梁的长度取梁跨度的反弯点位置。柱上下各取1 800 mm,截面尺寸为600 mm×400 mm×200 mm×200 mm,柱壁的厚度为12 mm,梁反弯点长度取1 500 mm,截面尺寸为400 mm×200 mm×8 mm×12 mm。
竖向加劲肋的形状见图1。厚度和柱壁厚度和钢梁翼缘厚度一致,为12 mm。

图1 竖向加劲肋形状
竖向加劲肋的高度取值满足[2]:
hs≥tbfbbf/(2ts)
(1)
式中:hs为竖向加劲板高度;
tbf为梁翼缘厚度;
bbf为梁翼缘宽度;
ts为竖向加劲肋厚度。
由式(1)可计算得出,hs≥100 mm。
竖向加劲肋与梁翼缘的连接长度l1取值满足[3]:
l1≥M/(2hbtbffy)
(2)
式中:M为节点承受的梁端弯矩;
hb为钢梁截面高度;
fy为钢材抗拉强度设计值。
式(2)中,可计算得到,l1≥126.44 mm。
竖向加劲肋与柱壁采用搭接连接,在搭接连接中,搭接长度不得小于焊件最小厚度的5倍,并不得小于12 mm[4]。由此可以计算出竖向加劲肋与柱壁的搭接长度不小于60 mm,并且需要保证焊缝与柱壁焊缝的距离不小于100 mm,则本文取150 mm。
竖向加劲肋的l1取25 mm,h1取50 mm。节点的正视图和俯视图见图2、图3。

图2 节点正视图
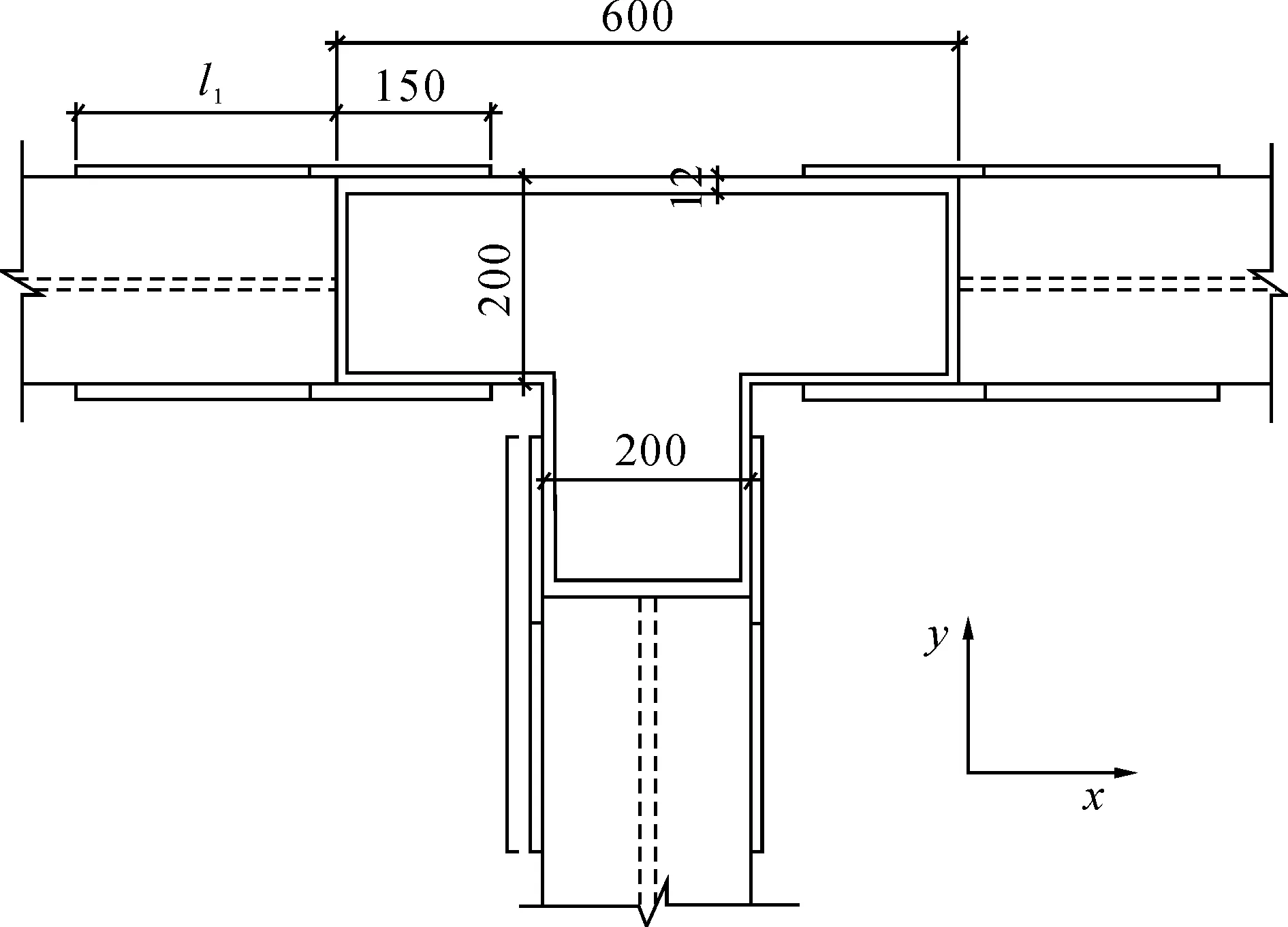
图3 节点俯视图
1.2 材料属性
柱钢管内灌注C35混凝土,其应力应变关系采用韩林海[5]约束混凝土本构关系模型,并通过有限元软件ANSYS计算得出混凝土的弹性模量E=2.251×104MPa,泊松比μ=0.2,采用多线性等向强化准则。钢材采用Q345钢,屈服强度标准值fyk=345 N/mm2,弹性模量E=2.06×105MPa,泊松比μ=0.3,采用理想弹塑性模型,双线性随动强化准则。
1.3 单元类型网格划分
节点模型中,钢管、钢梁以及竖向加劲肋选用Shell181单元进行模拟,核心混凝土采用Solid65单元进行模拟,焊缝位置采用节点耦合的形式进行模拟。节点有限元分析模型中焊缝不采用单独的单元模拟,焊缝连接节点彼此耦合。忽略钢管壁和混凝土之间的滑移影响。
网格采用映射法来划分,所有单元为六面体,为了能够提高分析效率以及较好精度,在节点区域的网格进行加密处理。具体的网格划分见图4、图5。

图4 混凝土网格划分图5 钢材网格划分
1.4 边界约束条件和加载方式
模型中钢管混凝土柱底部的x、y、z三个方向的平移自由度进行约束,对柱顶端边界的x、y方向平移自由度进行约束。梁端的约束则是两侧的梁端面弱轴约束y方向的水平平移自由度,中间梁端面弱轴约束x方向的水平平移自由度,这是为了防止梁在荷载作用下出现局部的侧扭屈曲。
模型加载是在柱顶端施加2 500 kN轴向压力,在梁端逐级施加z轴负方向位移荷载至100 mm。
2 节点受力性能的影响因素分析
通过改变竖向加劲肋的几何尺寸,分析其变化对于节点受力性能的影响,从中得出影响节点受力性能的因素以及竖向加劲肋合适的几何尺寸。
2.1 竖向加劲肋的高度对节点性能的影响
在本组模型中,仅改变竖向加劲肋高度hs,竖向加劲肋在高度上对称贴焊于柱壁与钢梁翼缘上。模型的竖向加劲肋尺寸见表1。
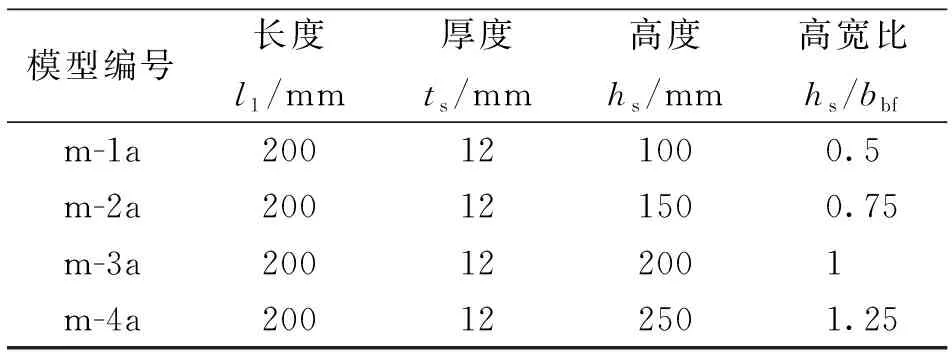
表1 模型竖向加劲肋尺寸表
本文采用倾角差值法[6]来计算节点转角θ,将荷载位移曲线斜率发生明显变化的点定为节点的屈服荷载。模型m-1a~m-4a左侧梁节点的弯矩-转角(M-θ)曲线见图6,以及节点的屈服荷载和初始刚度见表2。模型节点的中间梁的弯矩-转角曲线形状与图6类似,只是其开始阶段的斜率略小于图6所示的斜率。
从表2可以看出,随着竖向加劲肋高度hs的增加,不管是左侧梁还是中间梁,节点的屈服荷载和初始刚度均呈现先增长后减小的趋势,最大屈服荷载与最小屈服荷载的比值均为1.03倍,节点的最大初始刚度与最小初始刚度的比值大约为1.13倍。综合以上,竖向加劲肋的高度不宜过小,也不宜过大,略大于钢梁翼缘宽度的0.75倍,与钢梁翼缘宽度一致为宜。
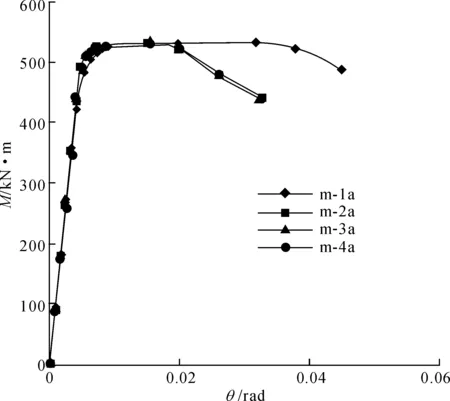
图6 模型m-1a~m-4a中左侧梁的弯矩-转角曲线

模型编号左侧梁屈服荷载/kN初始刚度/(kN·m/rad)中间梁屈服荷载/kN初始刚度/(kN·m/rad)m-1a319.9589 536.85323.8465 136.64m-2a328.2298 486.6331.5670 779.18m-3a329.33100 508.55332.8872 321.02m-4a330.30102 133.89334.0573 671.06
2.2 竖向加劲肋的厚度对节点性能的影响
在本组模型中,仅改变竖向加劲肋厚度ts。竖向加劲肋尺寸见表3。
模型m-1b~m-5b中左侧梁的弯矩-转角(M-θ)曲线见图7,以及节点的屈服荷载和初始刚度见表4。模型节点的中间梁的弯矩-转角曲线形状与图7类似,只是其开始阶段的斜率略小于图7所示的斜率。

表3 模型竖向加劲肋尺寸表
从表4可以看出,随着竖向加劲肋厚度ts的增加,左侧梁和中间梁的节点屈服荷载和初始刚度先增加后减小。尤其是当竖向加劲肋厚度从8 mm增加至12 mm时,节点的屈服荷载和初始刚度均有一个较大的增加,随后增长趋势渐渐变缓。最大屈服荷载与最小屈服荷载的比值均为1.07倍,节点的最大初始刚度与最小初始刚度的比值大约为1.16倍。综合以上,竖向加劲肋的厚度应略大于钢梁翼缘的厚度,其ts/tbf略大于1比较合适。

图7 模型m-1b~m-6b中左侧梁的弯矩-转角曲线
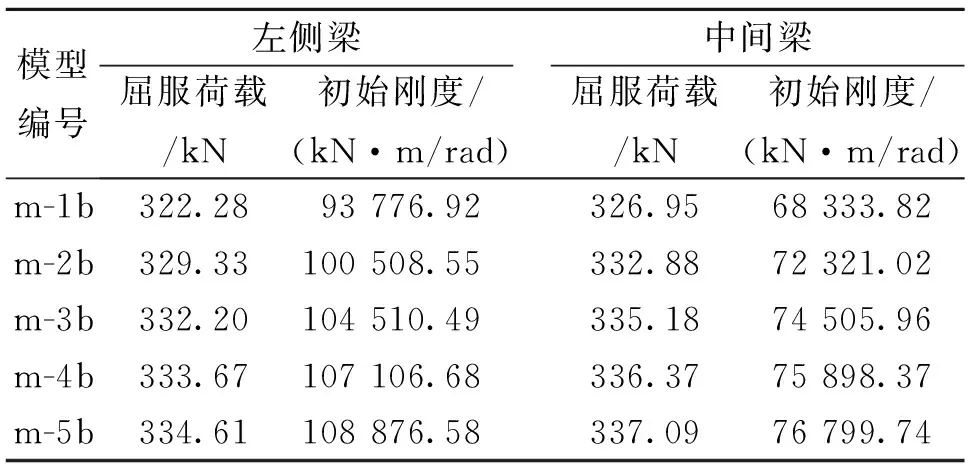
模型编号左侧梁屈服荷载/kN初始刚度/(kN·m/rad)中间梁屈服荷载/kN初始刚度/(kN·m/rad)m-1b322.2893 776.92326.9568 333.82m-2b329.33100 508.55332.8872 321.02m-3b332.20104 510.49335.1874 505.96m-4b333.67107 106.68336.3775 898.37m-5b334.61108 876.58337.0976 799.74
2.3 竖向加劲肋与钢梁翼缘的连接长度对节点性能的影响
在本组模型中仅改变竖向加劲肋与钢梁翼缘的连接长度l1。取竖向加劲肋的几何尺寸参数见表5。
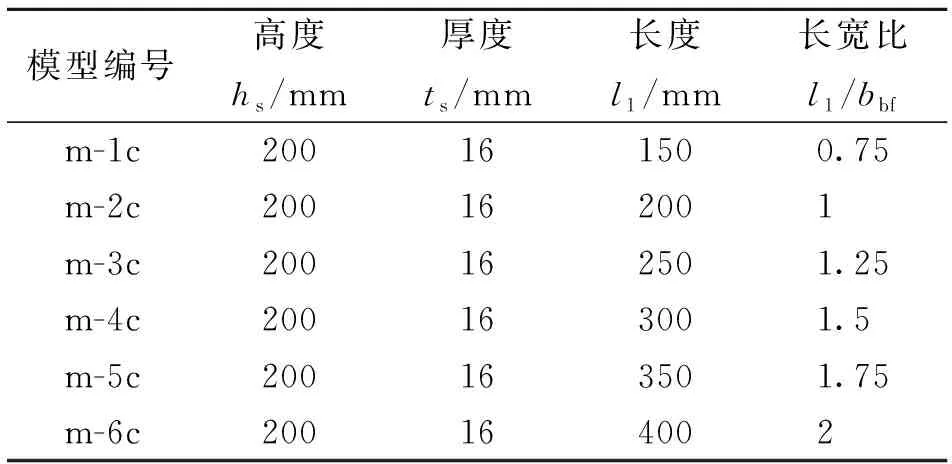
表5 模型竖向加劲肋尺寸表
模型m-1c~m-6c中中间梁的弯矩-转角(M-θ)曲线见图8,以及节点的屈服荷载和初始刚度见表6。模型节点的中间梁的弯矩-转角曲线形状与图8类似,只是其开始阶段的斜率略大于图7所示的斜率。

图8 中间左侧梁的弯矩-转角曲线
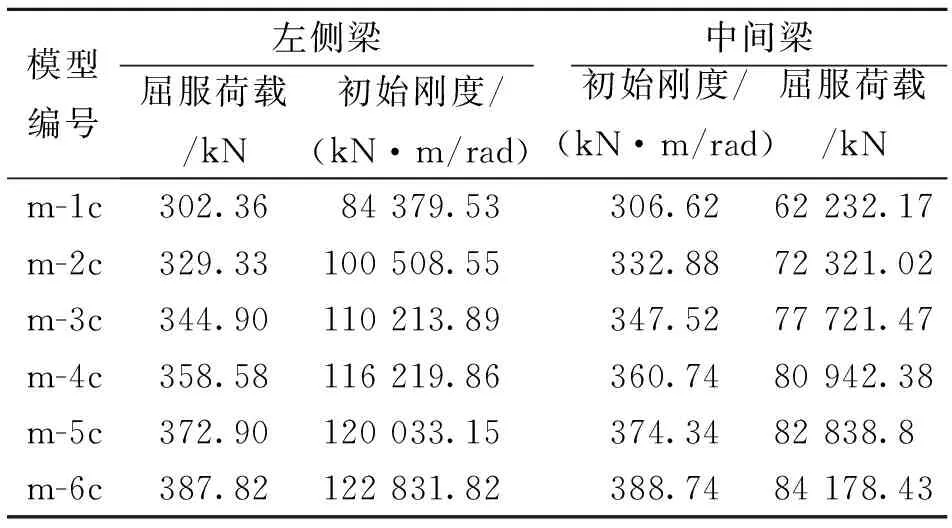
模型编号左侧梁屈服荷载/kN初始刚度/(kN·m/rad)中间梁屈服荷载/kN初始刚度/(kN·m/rad)m-1c302.3684 379.53306.6262 232.17m-2c329.33100 508.55332.8872 321.02m-3c344.90110 213.89347.5277 721.47m-4c358.58116 219.86360.7480 942.38m-5c372.90120 033.15374.3482 838.8m-6c387.82122 831.82388.7484 178.43
从表6可以看出,随着竖向加劲肋与钢梁翼缘的连接长度l1的增加,节点的屈服荷载和初始刚度先是有较大的增加,然后增长趋势渐渐变缓。最大屈服荷载与最小屈服荷载的比值均为1.28倍,节点的最大初始刚度与最小初始刚度的比值大约为1.46倍。
模型m-1c~m-6c中节点的延性系数见表7。节点的延性系数由极限位移与屈服位移的比值来确定。

表7 模型延性系数表
从表7可以看出,随着竖向加劲肋与钢梁翼缘的连接长度l1的增加,节点的延性系数逐渐下降,最大延性系数与最小延性系数的比值大约为1.45倍。
综合以上,竖向加劲肋与钢梁翼缘的连接长度l1应略大于钢梁翼缘的宽度,其l1/bbf应该在1.0~1.5比较合适。
3 结 语
通过分析竖向加劲肋的各尺寸对节点性能的影响,得出结论:竖向加劲肋的高度、厚度和与钢梁翼缘的连接长度的增加,都能对节点的屈服荷载和初始刚度起到提高作用;相比较于竖向加劲肋的高度和厚度,与钢梁翼缘的连接长度对于节点的屈服荷载和初始刚度提升最为明显。竖向加劲肋合理的尺寸为:高度略大于钢梁翼缘的0.75倍,厚度略大于钢梁翼缘厚度,与钢梁翼缘的连接长度应略大于钢梁翼缘宽度。
