平原混合圩区排涝模数理论模型的研究与改进
2018-12-28果利娟管桂玲张玉兰贾本有
陈 璇,果利娟,管桂玲,张玉兰,贾本有
(1.南京市水利规划设计院股份有限公司,南京 210022;2.宁波市水利水电规划设计研究院,浙江 宁波 315192;3.南京水利科学研究院水工水力学研究所,南京 210029)
在平原河网或沿江滨湖等低洼地区,河湖的洪水位往往高于两岸农田的地面高程,为了防止外洪倒灌淹没农田,人们常采用筑堤成圩的方式挡水于圩外,随着联圩并圩的发展,圩田规模不断扩大,河网、湖泊、滩地、城镇及农村等均被圈入圩内,从而形成现在的圩区。圩区的建设达到了围田于内,挡洪于外的效果,同时圩区内部通过开沟渠,设涵闸,建泵站实现排水利田的目的。合理的配置圩区的排涝动力是圩区排涝体系构建的重要内容之一,罗文兵等[1]采用经验公式法和平均排除法计算不同排涝标准下的排涝模数,并分析了2 种计算方法中排涝天数、排涝模数及排涝重现期之间的关系;周建康等[2]以太湖流域圩区为实例,分析了圩区设计排涝模数计算的数学模型,得出设计排涝模数与水面率之间的二次抛物线关系。
随着圩区内社会经济的发展,许多圩区从传统的农业圩演变为城市圩、半城市圩,圩内的保护对象、排涝标准、排涝要求均发生了变化,而现有的排涝计算方法多适用于传统的农业圩区,已不能满足现阶段圩区排涝计算的需要。吕刚[3]等分析了城市圩区与农业圩区在排涝标准、排涝流程及计算公式等方面的差异,利用表解法探讨了二者排涝计算方法;崔韩[4]等以常熟市为例对城市圩区、农业圩区排涝模数进行计算,并分析了两种圩区不同的排涝要求对排涝模数计算方法的影响。
本文在现有圩区排涝计算方法的基础上,综合考虑城市圩区及农业圩区排涝特点,对水量平衡法进行了改进以满足混合圩区的排涝计算需要。
1 现有排涝计算方法
1.1 平均排除法
根据《灌溉与排水工程设计规范》(GB50288-99),平均排除法公式如下:
(1)
式中:q为泵站向外河机排的设计排涝模数,m3/(s·km2);P为历时为T的设计暴雨量,mm;A为排水区总面积,km2;Aw为水田面积,km2;A1为河网、沟塘及水面面积,km2;A2为河网、沟塘水面面积,km2;A3为旱地及非耕地面积,km2;h1为水田蓄滞水深,mm;h2为河网、沟塘蓄滞水深,mm;h3为旱地及非耕地初损与稳渗量,mm;Ew为历时为T的水面蒸发量,mm;F为历时为T的水田渗漏量,mm;t为泵站1 d内的运转时间,h;T为排涝历时,d。
该方法主要用于农业圩区泵站设计排涝模数[5],排涝模数计算值主要影响因素为设计暴雨量、泵站运行时间和河网沟塘调蓄能力,调蓄时间一般取1~2 d对应的泵站开机时间,计算排涝模数值较小,且要求圩区应具备一定的耐淹能力。
1.2 峰值平均排除法
城市治涝标准一般要求在排除时间内最高内涝水位控制在设计水位以下;农田治涝标准为从作物受淹起,经济作物和旱作物在排除时间内排至田面无积水,水稻田在排除时间内排至作物耐淹水深[6]。由于城市圩区与农业圩区在排涝标准、排涝历时要求不同,且圩区的下垫面组成、河网沟塘调蓄能力亦不同,不能直接利用平均排除法计算城市圩排涝模数,目前江苏、安徽等地区常用峰值平均排除法作为城市圩排涝模数计算方法[7]。该方法针对城市圩要求涝水及时排出的特点假设圩区沟塘调蓄能力只在洪峰期间发挥作用,通过沟塘调蓄后的峰值时段出流量即为圩区所需的排涝流量。具体公式如下:
(2)
式中:q为泵站向外河机排的设计排涝模数,m3/(s·km2);m为内河入流过程峰值时段长,h;Ri为峰值i时段内河入流水量,mm;k为圩内可调蓄水面率;h为圩内沟塘调蓄水深,mm。
1.3 混合圩计算方法
目前常用的混合圩排涝计算方法为面积权重法,公式为:
(3)
式中:qp为圩区综合排涝模数,m3/(s·km2);qd为城镇区域的设计排涝模数;qw为农村区域的设计排涝模数;Ad为城镇面积,km2;Aw为农田面积,km2。
该方法以圩区内城镇面积与农村面积作为权重推算整个圩区的综合排涝模数,该方法原理相对简单,便于理解,目前广泛使用。
1.4 现有排涝计算方法存在的问题
农业圩和城市圩排涝特点不同,主要体现在以下几方面:
(1)排涝标准不同,农业圩一般要求圩内涝水1~2 d排出,排涝重现期多为10~20 a一遇;而城市圩一般要求圩区涝水24 h内及时排出,排涝重现期多为20~30 a一遇;
(2)排涝要求不同,农业圩一般要求排涝期末涝水排至农作物耐淹水深,且允许短时间内的淹没,城市圩要求排涝期内涝水不超过圩区最高涝水位,涝水要及时排出[8]。
目前混合圩区排涝计算常用的面积权重法虽然原理简单,计算方便,但该法不能反映农业圩和城市圩的排涝特点,当圩区内城镇布局较为集中,建成区地面高程明显高于圩内水田高程,排涝期农田受淹不会影响城镇区域的正常排水时,采用该法计算结果相对合理;当圩区内城镇布局较为分散,农田与城镇之间无明显高差时,采用面积权重法往往会造成建成区的排水不畅,间接的降低了圩内城镇区域的排涝标准。
2 混合圩区排涝模数计算方法的改进
本文在总结现有排涝计算方法优缺点的基础上,综合考虑城市圩区及农业圩区排涝特点,对水量平衡法进行了改进以满足混合圩区的排涝计算需要。
2.1 水量平衡法
水量平衡法原理如下:
(4)
式中:Vt+1、Vt分别为t+1时刻与t时刻的圩区调蓄水量,m3;Qt+1、Qt分别为t+1时刻与t时刻的圩区产流量,m3/s;qt+1、qt分别为t+1时刻与t时刻的外排流量,m3/s;Δt为计算时间步长,h。
该法按照来多少排多少的原则进行排涝调度,即当圩区产流量小于圩区排涝能力且圩内无待排涝水时按来水量抽排涝水,当圩区产流量大于圩区排涝能力或圩内有待排涝水时增大外排流量,控制qt≤qmax,qmax为圩区排涝能力。设计洪水过程按照水量平衡法计算后得到各时刻圩内最高水位Zt,当圩内设计水位Zc 圩区排涝规模即要能够保证圩内保护对象的安全,同时又不能过大,造成排涝动力的浪费,即以工程效益最大化为目标函数,其目标函数通式可写成: maxF=max(f1-f2) (5) 式中:F为工程效益;f1为工程运行期间减少的灾害损失值;f2为工程的前期投资费用。 排涝工程在其设计标准下应该要确保保护对象的防洪安全,亦可认为排涝工程建成运行后遭遇设计标准洪水时,保护对象损失值基本为0,目标函数可简化为: maxF=min(f2) (6) 排涝工程的前期投资费用与工程选址、工程工艺、工程规模关系密切,工程选址、工程工艺往往受其他客观条件影响较大,本文不做研究,本文假设排涝工程的前期投资费用与工程规模呈线性相关关系,目标函数可写成: min(q)=min(a1q1+a2q2) (7) 式中:q为圩区总设计排涝模数;q1为圩内城镇范围的设计排涝模数;q2为圩内农田范围的设计排涝模数;a1、a2分别为城镇范围及农田范围权重。 城镇部分计算时主要约束条件为最高涝水位约束: Z1max≤Zmax (8) 式中:Z1max=max(Z11,Z12,…,Z1t),即计算过程中最高水位;Zmax为圩区允许控制的最高水位,其取值应根据城镇范围内最低高程处的设计最高涝水位及农田范围内考虑允许淹没的设计涝水位,二者取小值。 农田部分计算时主要约束条件为时段末水位约束: Z2end≤Zend (9) 式中:Z2end为农田范围内计算时段末水位;Zend为农田范围内计算时段末允许最高水位,其取值主要取决于农田高程及时段末农田耐淹深度。 在满足时段末水位约束条件的同时,为了适应城市圩排涝要求,确保农田排涝不影响圩区内的城镇排涝,农田部分排涝计算也需要满足最高涝水位约束: Z2max≤Zmax (10) 混合圩区排涝目标函数的求解,可借助计算机程序采用迭代计算,逐步逼近最优解,具体步骤如下(图1)。 图1 模型结构示意图Fig.1 Schematic diagram of model structure (1)确定圩区允许控制的最高水位Zmax和时段末水位Zend,其中Zmax一般以城市排涝允许最高水位为依据,Zend一般以农田耐淹水位为依据; (2)给定Q1和Q2初始值,为减少程序迭代次数可采用平均排除法等公式法的计算结果作为初始值; (3)城镇地区水量平衡计算,通过迭代计算,直至满足最高涝水位约束; (4)农田地区水量平衡计算,通过迭代计算,直至满足时段末水位约束; (5)农田地区水量平衡计算,通过迭代计算,直至满足最高涝水位约束。 同样的内涝发生在不同的地区,导致的结果可能会有所不同,说明洪涝灾害具有自然和社会双重属性。一般认为,社会经济条件发达的地区,由于人口和城镇密集以及产业活动频繁,区域内受内涝灾害影响时,人员伤亡和经济损失比较大,其排涝要求就高,排涝计算时权重就应该高,而人口、经济载体较少的农村地区由于受灾损失较小,影响有限,其排涝要求可以适当降低,对应的排涝计算时的权重就相对较小。本次采用层次分析法确定排涝计算权重,采用地区固定资产、地区人口数、地区二、三产业总产值、地区第一产业总产值四个指标因子反映该区域的经济、人口的特征。构建指标因子判断矩阵,在各因素之间两两比较时,为进行量化,引入标度1~9,分别表示两因素之间的相对重要性,1表示两者一样重要,9表示前者绝对重要于后者,判断矩阵见表1。 表1 损失判断矩阵Tab.1 Judgment matrix of waterlogging loss 求解损失判断矩阵最大特征值,其对应特征向量即为指标因子间的权重,结果见表2。 表2 指标因子权重计算成果表Tab.2 Results of Index factor weight 指标因子标准化后进行加权得到城镇范围与农田范围的排涝计算权重。 考虑到各指标因子量纲差别较大,为消除各指标的量纲效应,采用下式对指标因子进行标准化: uij=xij/[max(xi)+min(xi)] (11) 式中:uij为第j区第i个指标的标准化值;xi为第i个指标的原始值。 周岗圩位于南京市江宁区东南部,属秦淮河流域中下游地区,北、西、南三面被句容南河、溧水河、二干河所环抱。圩区总面积42.5 km2,其中耕地面积3 313.33 hm2,圩内地面高程基本在5.0~10.0 m。周岗圩现建有涵洞9座。建有固定排涝站14座50台,排涝流量33.9 m3/s。 圩区原为农业圩,以水田为主,随着江宁区城市化发展的加快,周岗镇面积不断增大,圩区由传统的农业圩逐渐演变为半城半农的混合圩区,圩内原有排涝泵站规模是按照农业圩排涝标准建设,已不能适应周岗圩内社会发展的需要。 采用层次分析法计算周岗圩城镇范围与农田范围的排涝计算权重,结果见表3。 (1)排涝标准。周岗圩作为混合圩区,其城镇范围按照20 a一遇最大24 h降雨,圩内最高水位不超过设计水位要求控制,农田范围按照20 a一遇最大24 h降雨,雨后一日排至耐淹水深要求控制。 表3 城镇范围与农田范围排涝权重计算表Tab.3 Weight of drainage in urban area and farmland area (2)设计暴雨。采用临近的前垾村雨量站1960-2017年最大一日降雨资料进行频率分析,得到研究区20 a一遇设计降雨为224.7 mm,采用《江苏省暴雨图集》最大24 h典型降雨过程进行雨型分配,最终得到设计暴雨过程,并采取径流系数法推求设计产流过程,结果见表4。 表4 20年一遇设计暴雨及设计产流过程Tab.4 Design rainstorm and design runoff process in 20 years (3)水位蓄量曲线。采用arcgis软件对周岗圩地形数据进行统计分析,结果见表5。 表5 周岗圩水位蓄量关系Tab.5 Zhougangyu water level storage relationship (4)约束条件。根据高程统计结果分析,城镇范围内最低点地面高程约为5.8 m,考虑0.5 m安全超高,最高控制水位确定为5.3 m。水田范围内最低点地面高程约为5.0 m,水稻耐淹水深3~30 cm,本次按照3 cm取值,因此期末控制水位取5.03 m。 (5)初始值。由于周岗圩水系间相互串联,综合考虑城镇排水安全及水田地区灌溉需要,初始水位不宜降低太多,汛期按照城镇范围内最低点0.5 m调蓄水深考虑,河道初始水位取4.8 m。 (6)水量平衡计算。采用改进后的混合圩区水量平衡法计算周岗圩20年一遇设计排涝流量,城镇范围计算过程见表6,混合圩区排涝计算结果见表7。 从结果看,当仅考虑圩内涝水位约束条件不考虑受灾区淹没损失差异性时,周岗圩总排涝流量需62 m3/s,若按照保护对象受灾损失情况进行加权,其排涝流量为73 m3/s。 表6 城镇范围水量平衡计算过程Tab.6 Calculation process of urban area water balance 表7 水量平衡计算结果统计表Tab.7 Statistical table of water balance calculation results 采用常用的面积权重法对周岗圩排涝模型进行分析计算,并与本文提出的改进水量平衡法计算成果进行比较,结果见表8。从结果看,传统的面积权重法中城镇范围排涝流量是采用2 h峰值排除法计算得到,其结果与水量平衡法较接近,而农田范围采用的平均排除法的计算结果小于改进后的水量平衡法的计算结果,从前文计算可知,该流量偏小,会造成排涝期圩内水位超最高控制水位,间接的降低了城镇范围的排涝标准。 表8 不同排涝计算方法结果对比表Tab.8 Comparison table of results of different drainage calculation methods 本文在总结国内常用的混合圩区排涝计算方法的原理、特点和适用范围的基础上,从混合圩不同保护对象排涝要求出发,以水量平衡法为基础,对该法进行了改进以适应混合圩区排涝计算要求,并以周岗圩为算例,对模型实用性进行了验证,得出以下结论。 (1)国内混合圩区排涝计算多采用面积权重法,该法往往忽略了城镇地区与农田地区排涝标准及排涝要求的区别以及保护对象的受灾损失的差异,其计算成果往往偏低,间接降低了城镇地区的排涝标准。 (2)本文对水量平衡法进行了改进,在农田地区的排涝计算中引入了最高控制水位及期末水位等约束条件,使得农田地区排涝计算中不仅考虑了本地区的排涝同时兼顾了城镇地区的排涝要求,同时引入排涝权重的计算方法,定量的反映了保护对象的重要性。采用该法对周岗圩排涝动力进行了复核,成果基本合理。 □2.2 混合圩区水量平衡法
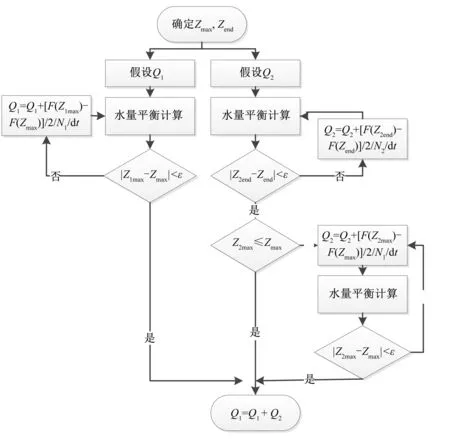
2.3 城镇范围及农田范围排涝计算权重确定


3 算 例
3.1 排区概况
3.2 排涝权重计算
3.3 排涝模数计算

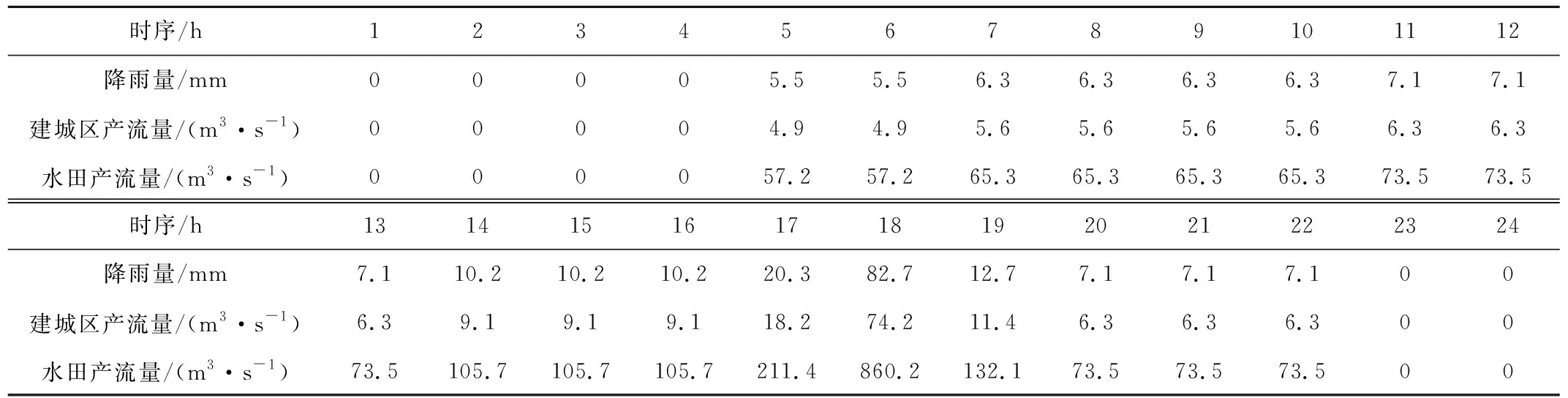



3.4 不同方法对比分析
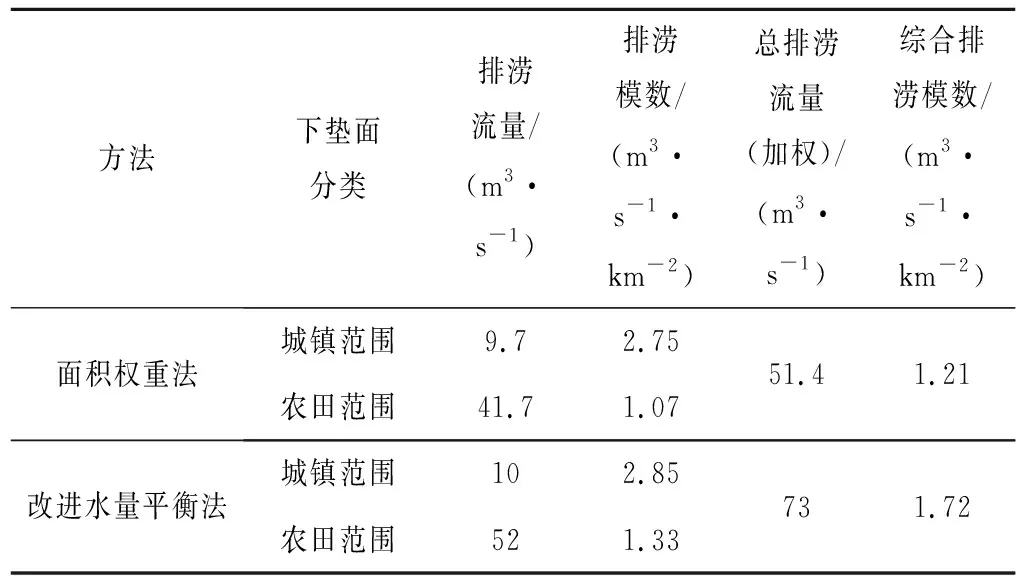
4 结 语
