一类时滞网络病毒传播模型局部Hopf分支
2018-12-28胡笑梅华纯良王有刚张子振
胡笑梅,华纯良,王有刚,张子振
(安徽财经大学管理科学与工程学院,安徽蚌埠233030)
随着计算机技术和网络技术的不断发展,网络信息系统已经成为推进一个国家、乃至整个人类社会发展前进的重要手段,与此同时,信息安全问题也为日常工作过程中的信息共享带来了挑战,最典型的一个信息安全威胁便是计算机网络病毒传播。为了有效防止网络病毒的传播,国内外不少学者基于微分方程理论提出了多种利用网络病毒传播模型,并取得了一定的研究成果[1-4]。文献[2]研究了一类具有非线性免疫率的SIRS计算机网络病毒传播模型,文献[5-7]研究了不同形式的具有分级感染率的计算机网络病毒传播模型。但是,以上多数模型并未考虑反病毒软件的免疫作用。最近,文献[8]研究了如下具有直接免疫的SIRSA计算机网络病毒传播模型的稳定性:其中,S(t)、I(t)、R(t)和A(t)分别表示易感主机、已感染主机、恢复状态主机和免疫状态主机(安装有反病毒软件)在时刻t的数量,C表示网络中主机的常数接入率,αSA表示易感主机转化为免疫主机的几率,αIA表示已感染主机转化为免疫主机的几率,β表示易感主机的感染率,μ表示主机的自然“死亡”率,δ和σ均为状态转移率。但是,文献[8]并未考虑网络病毒在传播过程中的时滞因素。众所周知,时滞对动力系统的稳定性有着非常重要的影响,它可以使得一个动力系统由稳定变得不稳定,从而引起系统产生Hopf分支。

Hopf分支是一种非常重要的非线性现象,对于计算机网络病毒传播模型而言,这种现象表明模型所描述的网络中几类主机数量将由一种理想的稳定状态进入周期震荡状态,这将不利于网络中计算机病毒传播的有效控制。因此,研究计算机网络病毒传播模型的Hopf分支现象,对于计算机网络病毒传播的控制具有重要的理论指导意义[9]。同时,考虑到计算机网络病毒的潜伏期,本文在模型(1)中进一步引入计算机网络病毒的潜伏期时滞,得到下列具有时滞的SIRSA计算机网络病毒传播模型:

其中,τ为计算机网络病毒的潜伏期时滞。
1 Hopf分支的存在性
求解下列方程,
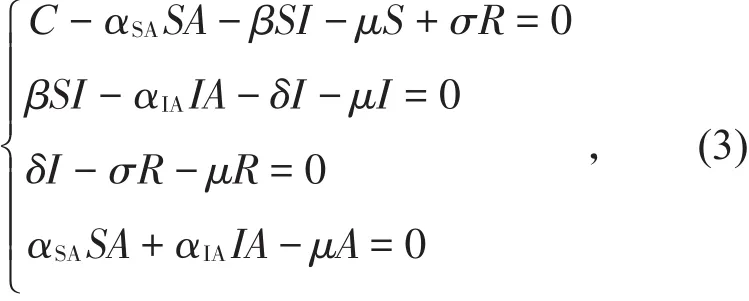
直接计算可得,如果条件(H1):

成立时,模型(2)存在唯一有病毒平衡点E*(S*,I*,R*,A*),其中,
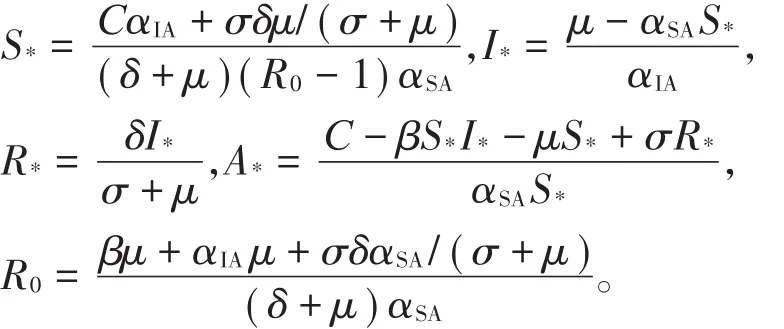
定理1对于模型(2),如果条件(H1)~(H3)成立 ,则 当 τ∈[0,τ0)时 ,有 病 毒 平 衡 点E*(S*,I*,R*,A*)是局部渐近稳定的;当τ=τ0时,模型(2)产生局部Hopf分支。
证明 模型(2)在E*(S*,I*,R*,A*)处的线性化部分特征方程为

当τ=0时,方程(4)变为
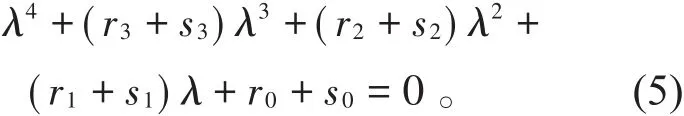
因此,根据赫尔维茨定理以及文献[8]分析可知,当1<R02<R03时,方程(5)的根均具有负实部,即模型(2)局部渐近稳定,其中,
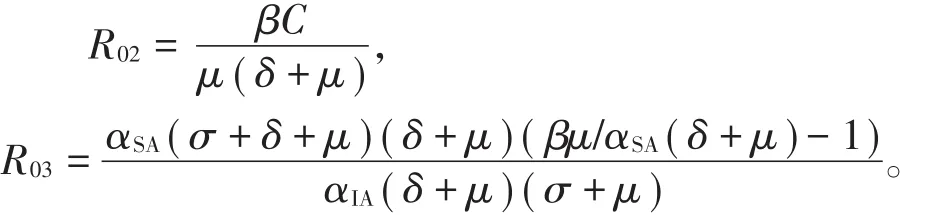
当τ> 0时,令λ=iω(ω > 0)为方程(4)的根,则

进而,有
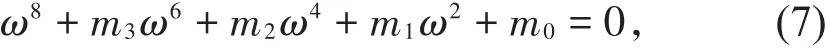
其中,

令 ω2=v,则方程(7)变为
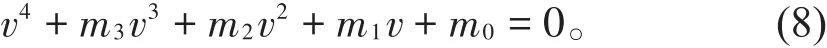
根据文献[10]中对方程(8)根的分布情况的讨论,我们假设
条件(H2):方程(8)至少存在一个正实根v0,则方程(7)存在正实根ω0=,进而方程(4)存在一对纯虚根±iω0= ±i。对于ω0,根据方程(6)可得
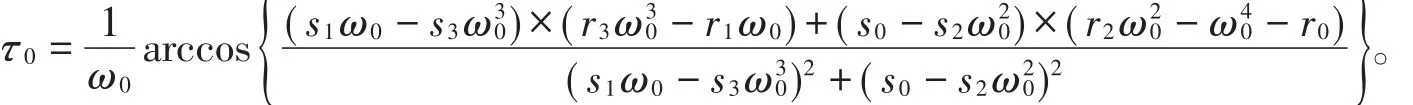
对方程(3)左右两边同时求λ关于τ的导数:
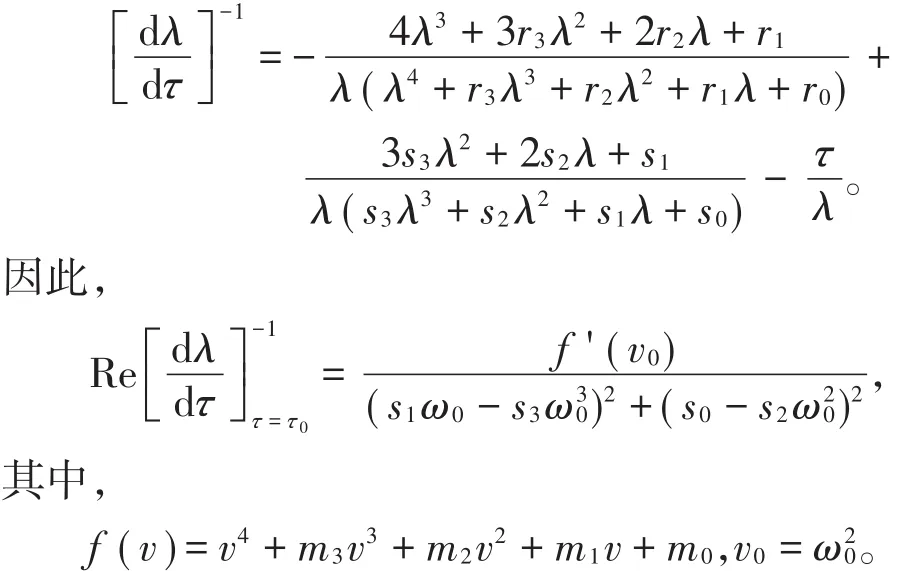

2 仿真示例
选取下列参数C=10,αSA=0.000 45,αIA=0.002 5,β=0.2,μ=0.05,σ=0.8,δ=10,则模型(2)变为
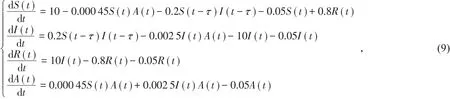
经过计算可知,系统(9)存在唯一有病毒平衡点E*(50.376,10.932 3,128.615 3,10.072 3),进而计算得到ω0=0.966 8,τ0=0.458 7。根据定理1可知,当τ∈[0,τ0)时,系统(9)渐近稳定,仿真效果如图1,图2所示。当τ>τ0时,系统(8)失去稳定并在τ0=0.458 7附近产生局部Hopf分支,仿真效果如图3,图4所示。

图1 τ=0.35时,S-I-R相图
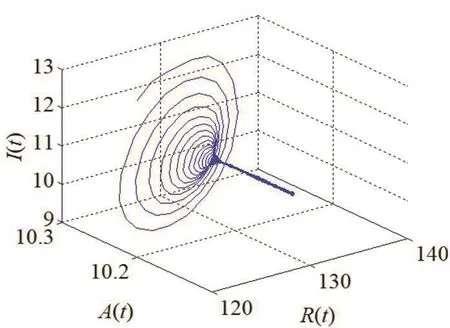
图2 τ=0.35时,I-R-A相图

图3 τ=0.525时,S-I-R相图
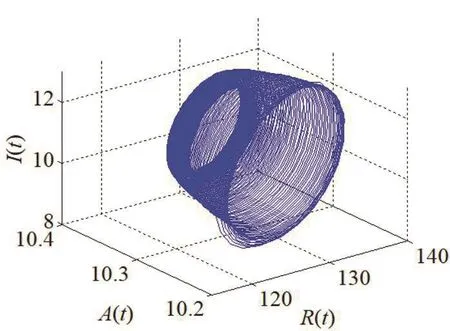
图4 τ=0.525时,I-R-A相图
3 结论
本文在文献[8]提出的SIRSA网络病毒传播模型的基础上,进一步引入了计算机网络病毒的潜伏期时滞。相对于文献[8],本文所研究的模型更具一般性,主要研究了时滞τ对模型稳定性的影响,所得结果是对文献[8]研究工作的补充。研究表明,当时滞τ的取值足够小时,可以更好地对计算机网络病毒的传播进行有效控制。一旦时滞τ的取值超越临界点τ0,模型将失去稳定,并在τ0附近产生局部Hopf分支。这种情况下,将不利于计算机网络病毒传播的控制。因此,应该对于模型的Hopf分支进行有效控制,以便保证模型处于理想的稳定状态。但是本文并没有对局部Hopf分支的性质进行研究,这个问题我们今后将作进一步研究。。
