初中数学动态几何问题教学研究
2018-12-27周海涛
周海涛
(江苏省如东县洋口镇初级中学 226400)
几何部分知识是初中数学教学的重要组成部分,是培养学生良好数学思维的重要内容,其中动态几何部分是几何部分的重点,也是数学新课程改革以来几何部分课程改革的重点.初中数学动态几何问题主要是以几何变换为主,是通过运动的观点去探究几何图形的变化规律.通过该部分知识的学习,不仅能够加强学生对唯物主义观念的理解,还有助于学生空间想象能力和抽象思维能力的发展,有助于学生对数形结合、分类讨论、转化与化归等多种数学思想的理解.
一、初中数学动态几何问题概述
初中数学动态几何问题涉及内容较为丰富,其中包含图形的性质、数量关系等内容,对学生数学思想方法的应用和探究能力要求较高.随着教育改革的发展与实施,初中数学动态几何问题成为了考查初中学生综合素质能力的重要题型,也是中考数学的一个重要考点,该部分知识涉及的题型较为广泛,不管是选择题、填空题还是解答题都能够看到动态几何的影子.其中,动态几何问题都是作为最后一题来出现,是整个试卷中难度系数最高的题目,它不仅考查学生对基础知识和基本技能的掌握情况,还考查学生的数学思想和数学能力的情况,是中考数学考试中令学生最为头疼的一类题目.很多数学基础稍微差点的学生会直接选择放弃该部分题目的求解,基础较好的学生也只是完成其中的部分问题的求解.从总体上来说,学生对于该类型题目往往存在一种逃避的心理,往往成为初中数学容易丢分的知识点.因此,研究如何提高学生动态几何问题的解题能力,提高动态几何部分内容的课堂教学效果,是数学教师需要研究的重点问题.
二、动态几何部分考点分析
通过对近些年中考数学试题的统计分析发现,动态几何问题是中考数学的热门考点,它往往是以压轴题的形式出现,并且考查的形式和题型灵活多样.具体来说,常考题型主要涉及到填空题、选择题和解答题以及综合题,考查知识形式分为点动问题、线动问题、图形运动问题和函数动点问题.虽然每年对动态几何考查的形式在变,但是整体的数学思想和题目结构几乎没有发生变化.从考查的知识形式来看,点动问题是常考的知识点,例如,苏州市近几年中考数学试卷中的动态几何问题,其中多是动点问题,因为该部分知识最接近数学考试大纲的要求.
三、初中数学动态几何部分教学建议
1.提高学生数学阅读能力
在中考数学中,考试时间一直是影响学生发挥的重要因素,提高学生的审题效率是关键.在中考中,学生面对阅读量较大的题目时,就会出现畏惧心理,从内心深处就不愿意在上边下功夫.在中考数学试卷中,动态几何问题往往是以大题的形势出现,阅读量相对加大,因此,提高学生数学阅读能力是提高学生动态几何解题能力的保障.
首先,要注重对基础知识的理解,对于基本概念、基本定理和数学公式要做到理解于心,能够在数学语言、符号语言、几何语言之间灵活转化,不能够死记硬背,这样才能够对所学的知识做到灵活应用.
其次,要培养学生精读题目的习惯,要看清题干中的每一个字,养成边看题目条件,边推导结论的习惯,根据题目中所给的已知条件,能够得出什么样的结论,需要在什么地方添加辅助线才能够向结论靠拢.同时,寻找题目中的隐含条件,对重点词语做好圈示.
第三,要带着数学思想去解题,这样便于学生寻找解题方法,提高解题效率.例如:如图所示,∠AOB=90°,OM为∠AOB的角平分线,在OM上有一点C,直角三角板的直角顶点与C点重合,OA与OB分别交直角三角板的两条边与点D、E,绕C点旋转三角板,使得CD与OA垂直,此时可以证明CD=CE.继续旋转三角板,使得CD与OA不垂直时(如图所示的位置),上述结论是否成立?如果成立请加以证明;如果不成立,请说明原因.
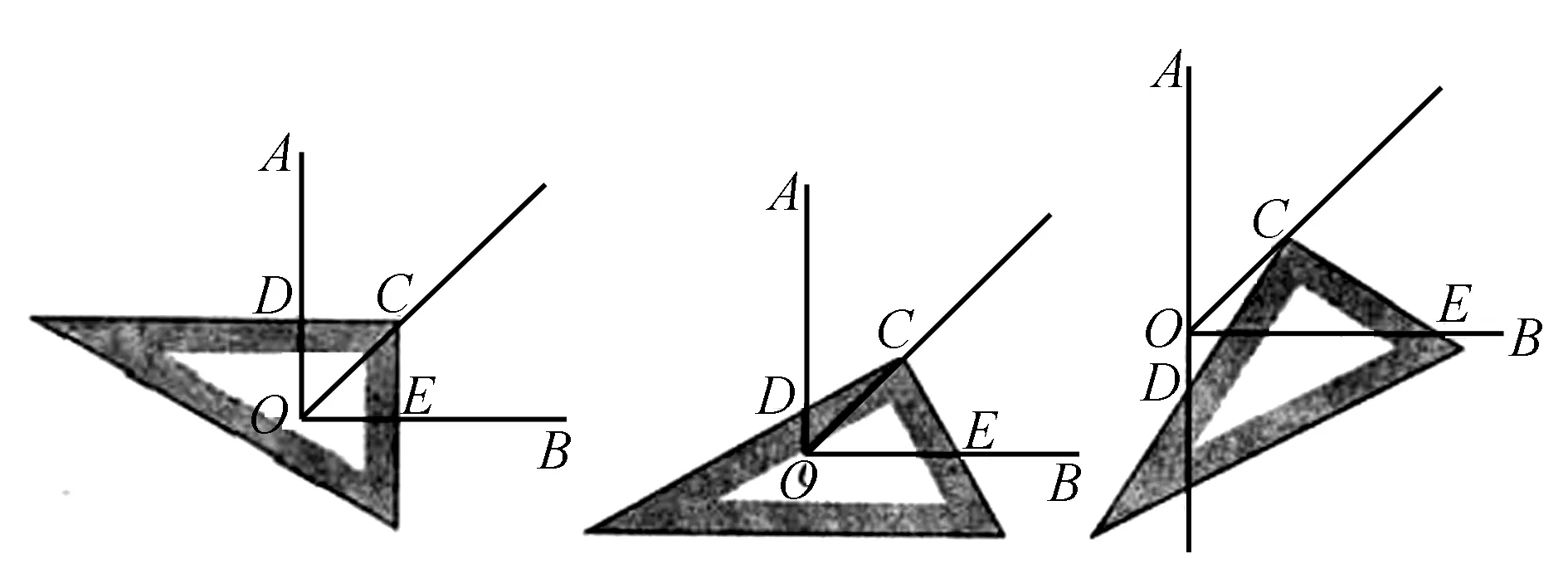
这道题题目看似很长,给人的第一感觉就是难以解决,导致学生产生畏惧心理,找不出图中所对应的全等三角形,但是利用类比的思想,就能够轻易地找到解题的突破口.
2.提高学生分类讨论思想意识
分类讨论思想是解决动态几何中动点问题的重要思想,在解决动点问题时必须要考虑是否需要进行分类讨论,找出题目中隐藏的所有可能性.通过平时的教学我们发现,很多学生出现动点问题解题错误的原因就是在于分类讨论时的漏解,这主要因为学生的分类讨论意识不高,不能够灵活地加以运用.因此,要提高学生在动点问题中的解题能力,提高学生分类讨论思想的应用意识是关键.
从数学教材上来看,蕴含着数学分类讨论思想的知识主要包括以下几个部分:第一,出现分类讨论思想情况存在于符号不确定的部分,主要在数与式中.例如,面对含有绝对值的有理数时,就需要对这一有理数进行正有理数、负有理数、0三种情况的讨论;涉及到有理数加法法则的运算时,就需要进行同号两数相加、异号两数相加和互为相反数的两数相加的分类讨论;涉及到带括号的运算时,还要根据去括号法则对正负数进行分类讨论.第二,分类讨论思想出现在方程或不等式中数量关系不确定的情况下,例如,不等式两侧同时乘以或除以一个正数或一个负数时;一元二次方程根的判别式大于0、等于0或小于0时,这些都需要进行分类讨论.第三,分类讨论思想出现在函数部分各项系数不确定的情况下,例如,对于二次函数y=ax2+bx+c(a≠0)的图象与性质会随着a,b,c的符号不同而发生变化,因此在分析该部分问题的时候,需要根据a,b,c的符号不同进行分类讨论.第四,分类讨论的思想还出现在图形性质部分的知识中.例如,在证明圆周角定理时,就需要对同一条弧线所对应的圆心角和圆周角之间的3种位置关系加以讨论.还有些通过问题表述就可以看出需要进行分类讨论.
例如,P点在从A点出发,沿着AB的方向运动.这种情况下,P点可以是在线段AB上运动,也有可能是在AB的延长线上运动,需要对它进行分类讨论.这些都需要教师在平时的教学中,有意识地向学生渗透这方面的思想.
3.提高学生的作图能力
在几何点动问题的解决中,很多学生之所以找不到解题突破口,主要原因就是作不出相应的图形,有些能够做出大体图形,但是作得不够标准,导致做题错误.这就要求教师在平时的教学活动中,要求学生不仅要学会作图,还要能够写出图形的画法,规范他们的语言表达和转化能力,提高学生作图的规范性.
初中数学动态几何部分是初中数学教学的重点,也是难点,同时也是近年来中考数学的热点,这就要求我们教师要结合自身专业知识,积极研究动态几何问题教学,提高学生解决动态几何问题的能力.
