城市扩展极限学习机模型

王 鹤，曾永年

1. 中南大学地球科学与信息物理学院，湖南 长沙 410083； 2. 中南大学空间信息技术与可持续发展研究中心，湖南 长沙 410083

进入21世纪，我国的城市化水平得到大幅度的提高，目前已进入城镇化快速发展时期。城市化的快速发展在带来巨大经济、社会效益的同时，也引发了社会与环境的问题。城市生活用地、工业生产用地的扩展与农业生产用地、生态用地的矛盾日益突出[1-2]，城市作为对生态环境影响最为深刻的区域，城市化过程对区域生态环境产生很大的影响[3]。为促进城市化过程的健康、可持续发展，城市土地资源的科学规划与管理就显得尤为重要。而城市空间结构及其扩展的科学模拟与预测是城市科学管理与规划的重要前提。为此，城市空间扩展过程的模拟与预测成为当前研究热点之一。

元胞自动机(CA)模型作为一种时间和空间都离散的网格动力型模型，能基于局部行为模拟复杂的全局变化。因此，CA模型具有模拟地理复杂系统演化的能力[4]。利用CA模型能够顾及城市区域宏观自然经济环境和土地利用局部变化[5]，从而实现对复杂城市化过程的模拟与预测。

在CA模型的构建与城市扩展模拟应用中，转换规则的确定是CA模型的关键，在CA模型中，有许多代表着经济或自然约束的变量，这些变量对应的参数代表着对应变量的贡献值，如何求取这些参数，是CA模型的难点[6-13]。逻辑回归较早的应用于元胞转换规则的提取，文献[14]基于线性Logistic回归获得CA模型转换规则并成功应用于广州城市的扩展模拟；文献[15]将逻辑回归、马尔科夫链和CA模型结合，有效地提高了模拟的精度；文献[16]利用逻辑回归探索了城市扩展驱动力对于城市发展的影响，以沈阳市1997—2010年城市建成区变化作为因变量，Logistic回归分析得到影响沈阳城市扩展的前几位驱动因子依次是开发区、距1997年城区距离、DEM、距高速公路和铁路距离、人口密度。已有研究表明逻辑回归较多元分析更能充分的揭示城市扩展规律，但在处理复杂的变量关系时难以表达研究区域的非线性变化。为了有效解决复杂城市系统模拟的问题，文献[17]将神经网络引入CA模型，利用神经网络获取土地利用转换规则，获得了比逻辑回归更高的模拟精度；文献[18]将神经网络与元胞自动机结合，从不同时相的遥感数据中挖掘城市扩展的演变规律，并对义乌市作了实证分析和模拟预测，与同期义乌市的发展基本吻合；文献[19]将神经网络与CA模型结合获取了理想的模拟结果。然而，已有的研究表明神经网络属于黑箱操作，且存在容易陷入局部最优解和收敛慢的问题。为此，将智能算法与CA模型结合的研究成为当前研究的热点之一，文献[20—21]提出了将蚁群智能算法和遗传算法等智能算法和元胞自动机相结合的模型，成功地应用于城市的模拟并取得了较好的结果；文献[22]利用多智能体与元胞自动机相结合的方法并成功模拟了上海市2005年城市扩展动态；文献[23]构建了一个基于博弈论的Cellular模型，并模拟了武汉市城市的发展进程，研究表明城市开发进程中不同利益相关者的权益冲突可以用博弈论来解决，相比于纯粹的CA模型，基于博弈论的Cellular模型拥有更高的模拟精度。智能算法所提取的规则不需要数学式表达，能方便地描述土地利用复杂的关系。然而，利用智能算法提取转换规则的过程相对复杂，算法复杂度较高，从而影响CA模型应有的简洁性。因此，构建结构简单，又能充分挖掘元胞转换规律的城市扩展模型是值得进一步探讨的问题。

近年来，在传统神经网络的基础上发展的极限学习机能够较好地解决神经网络算法速度慢、易陷入局部最优解等问题[24-25]。相比于智能算法，极限学习机的结构更为简单，能有效降低模型的复杂度；相比于神经网络，极限学习机不需要迭代求解，运行速度高且不易陷于局部最优解。因此，本文基于极限学习机，构建城市扩展的CA模型(ELM-CA)。在城市元胞结构设计的基础上，基于极限学习机自学习特性，有效挖掘城市空间扩展转换规则，以期为城市空间扩展模拟与预测提供更为准确、客观的技术方法。

1 ELM-CA城市扩展模型

1.1 极限学习机(ELM)理论基础

极限学习机是一种简单有效的单隐层前馈神经网络学习算法，能逼近复杂的非线性函数，具有泛化性能好、学习速度快等特点[26]。

极限学习机的网络结构如图1所示，其网络模型分为输入层、隐藏层和输出层。输入层有n个输入神经元，对应着输入数据的n个属性值；隐藏层有L个隐藏神经单元；输出层有m个输出神经单元，对应着数据的m个标签。Wij是第i个隐藏层神经单元与第j个输入层神经单元的链接权值，bi是第i个隐藏层神经单元的偏置值，βij是第i个隐藏层神经单元与第j个输出层神经单元的链接权值。假设有N个不同的样本(Xi,Yi)，其中i=1,2,…,N，Xi是属性数据，Xi=[xi1xi2…xin]，Yi是标签，Yi=[yi1yi2…yim]。极限学习机的网络可以表示为

(1)

式中，g(·)为激励函数，在极限学习机中激励函数要求无限可微。本文选择Sigmoid函数，上述方程用矩阵可以表示为

Hβ=Y

(2)

式中

(3)

(4)

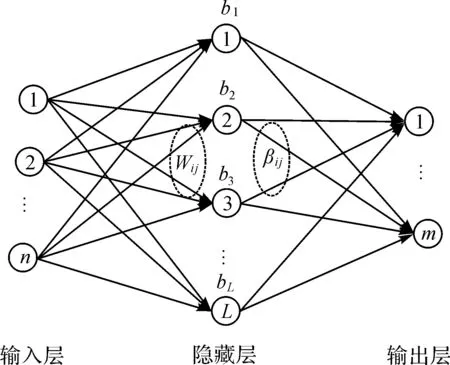
图1 极限学习机结构网络Fig.1 The structure of ELM

在极限学习机中，权值Wij和偏置bi被随机确定，所以上述矩阵方程中矩阵H是确定的，只有β是未知量。因此，极限学习机中参数的求解转换为解方程组Hβ=Y，可以得出

(5)

式中，Ht是H的Moore-Penrose广义逆，经过证明得到的解是唯一的。可以看出极限学习机的求解不需要迭代，所以非常高效，而且克服了传统基于梯度法所带来的局部最小解与过拟合的弊端。

1.2 ELM-CA模型

1.2.1 元胞状态及转换概率

以30 m×30 m分辨率的栅格空间作为元胞空间，元胞状态设置为：城市用地、耕地、林地、水域、裸地。在元胞的转换过程中，作如下假定：河流、湖泊等水域不发生转化，城市用地不向非城市用地转化。

非城市用地转换为城市用地的概率(P)一般取决于元胞转换为城市用地的潜力(PELM)、元胞邻域影响(Pneighbor)、随机因素(Prandom)影响。为此，本模型中元胞转换概率(P)可表达为

P=PELM·Pneighbor·Prandom

(6)

元胞转换潜力(PELM)：极限学习机能够很好解决复杂的非线性问题，非常适合地理等复杂现象。因此，本文利用极限学习机分别提取各主要非城市用地(耕地、林地、裸地)元胞转换为城市用地的潜力(PELM)。

每一个模拟的元胞单元有n个驱动因子(空间距离变量、自然属性要素)，对应于输入层的n个神经单元，而极限学习机的输出层对应于该元胞单元转化为城市的潜力。由式(1)可得，元胞的转化潜力PELM为

(7)

为了充分考虑不同用地类型转化为城市用地的差异，按主要非城市用地(耕地、林地、裸地)的历史数据分别采样，获得不同用地类型转换为城市用地的数据，并分别计算出各用地类型对应的模型参数，这样在计算中心元胞城市化潜力的时候，就用与中心元胞用地类型相同的模型参数，这样就可以充分考虑不同用地类型带来的影响。

邻域影响(Pneighbor)：Pneighbor是邻域城市元胞对中心元胞城市化的贡献值，Pneighbor由公式得出

(8)

关于中心元胞邻域的定义，本研究采用扩展摩尔型，其中con是条件函数，Sij是该元胞的状态。

随机因素影响(Prandom)：Prandom是0～1之间的随机值，用来模拟实际中的随机因素的影响，使模拟结果更加符合真实情况。

1.2.2 模型流程

CA模型通过多次的循环迭代，将邻域元胞的影响纳入模型，体现出元胞间局部相互作用，因为每次循环城市用地都会增加，所以邻域影响每次循环后也会改变。假设从初始年份到目标年份，城市元胞数目增加数量Q，总的循环次数为N，则每次循环增加的城市元胞个数为Q/N，模型的运行过程如下：

(1) 首先利用训练好的极限学习机根据驱动因子计算出每个元胞的转换潜力值(PELM)，基于初始年份的城市用地空间分布计算出邻域影响值(Pneighbor)，随机生成随机因素影响值(Prandom)，然后将三者相乘得到转化概率(P)。根据转化概率的大小，选择前Q/N个元胞作为新的城市元胞。

(2) 根据新的城市用地空间分布计算新的邻域影响值(Pneighbor)，随机生成新的随机因素影响值(Prandom)，转换潜力值(PELM)不变。然后根据得到的新的转化概率(P)，按大小选择前Q/N个元胞作为新一轮迭代增加的城市元胞。

(3) 重复第(2)步，直到总共新增的城市元胞等于Q，或者循环次数达到N。

模型运行的流程如图2所示。

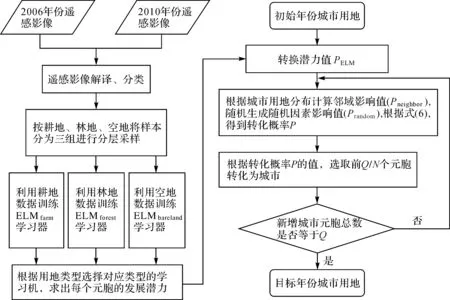
图2 模型运行流程Fig.2 The flow chart of the model

2 应用实例

2.1 试验区

本文的研究区域是长沙市主城区。长沙市位于中国东南部，湘江下游地区，是湖南省政治、经济、文化中心。地理区域为111°53′E—114°15′E，27°51′N—28°41′N。长沙市气候温和、降雨充沛，属于亚热带季风性气候。长沙市地形起伏大，东西部山地环绕，中部较为缓和；地貌类型多样，以山地、丘陵、平原为主；土壤以红壤和水稻土为主，适合多种农作物生长。试验区如图3所示。

2.2 试验数据及处理

利用2006、2010年两个时相的LandsatTM遥感影像监督分类得到的土地利用数据，该土地利用数据中将土地利用类型划分为城市用地、耕地、林地、水域和裸地。两期遥感影像的分类精度都达到80%以上，满足模拟试验的要求。本文试验使用的交通道路数据为1∶400 000的湖南省城市电子地图(2006年)，DEM数据来源于中国科学院计算机网络信息中心国际科学数据镜像网站。

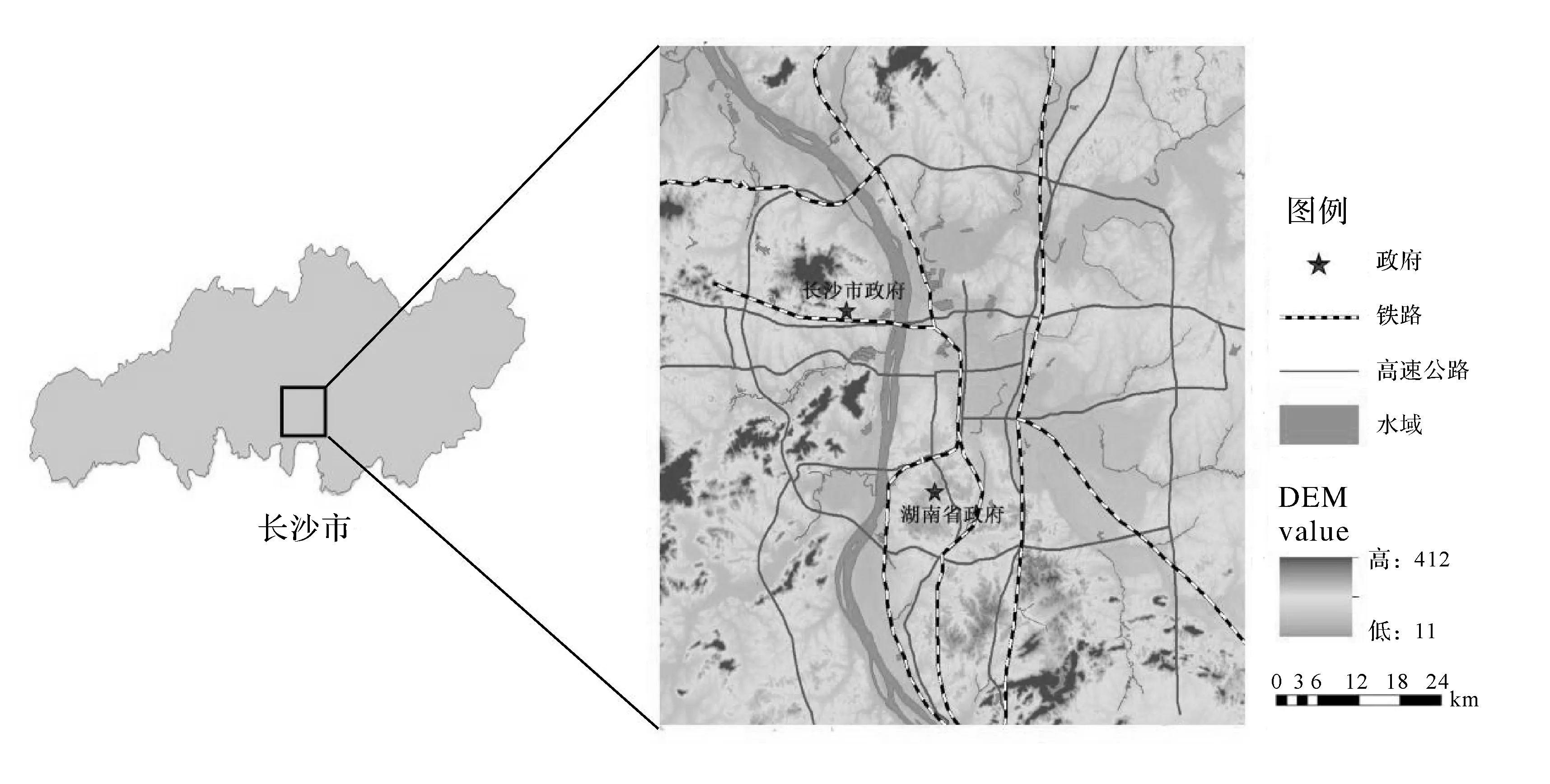
图3 试验区示意图Fig.3 Location of the research area

为了确定城市的扩展因子对中心元胞城市化潜力的影响大小，本模型选择了空间距离、自然属性两大类城市扩展驱动因子(表1)作为极限学习机的输入变量，各空间距离变量利用ARCGIS软件中的“距离分析”工具获得；自然属性变量中的坡度数据基于DEM数据，利用ARCGIS软件中的“坡度”计算模块获得；地形起伏度数据基于DEM数据，利用式(9)通过移动网格计算获得

R=H+[ΔH×(1-S/A)]

(9)

式中，R为中心单元的地形起伏度；H为网格内的平均高程；ΔH为网格内的高差；S为网格内的平地面积；A为网格面积。

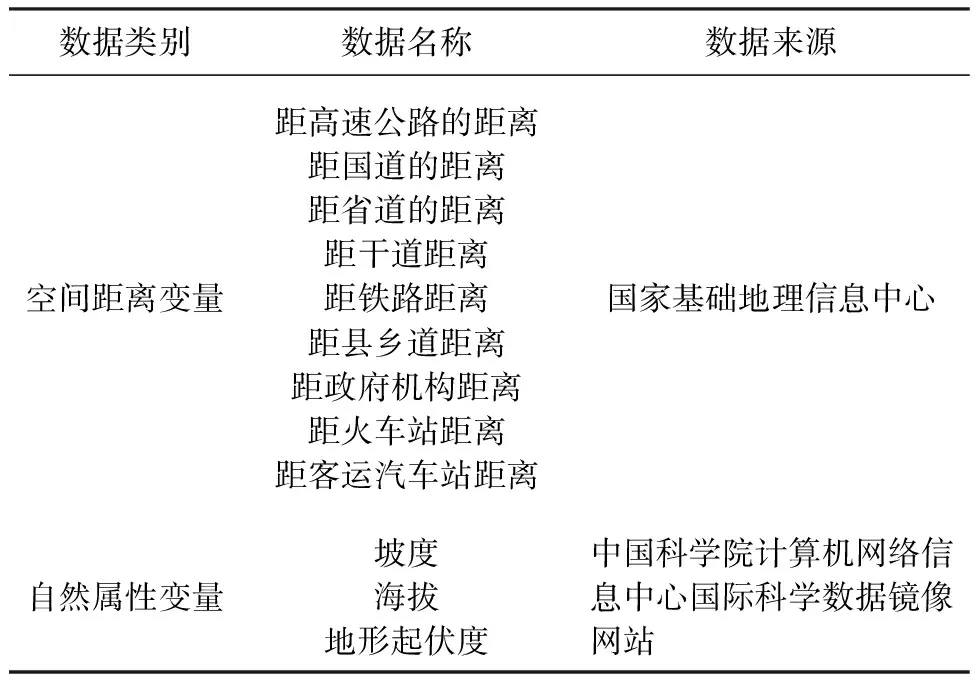
表1 城市扩展驱动因子

在输入极限学习机之前，对上述驱动因子进行归一化处理，以消除量纲的影响，同时也加快模型的训练速度。

2.3 模型训练与参数校准

为了构建ELM-CA模型，首先，基于历史数据对极限学习机进行训练，将2006—2010年期间转变为城市用地的元胞编码为1，没有发生转变的元胞编码为0，作为模型预测的目标变量。其次，利用随机分层采样的方法，从转变为城市用地的元胞和没有转变为城市用地的元胞中随机选择20 000个元胞作为样本，获取这些样本对应的归一化处理后的驱动因子和目标变量，由此构成样本数据集。然后，把样本数据集分为训练数据和测试数据，比例约为7∶3，训练数据用于训练模型获取学习器参数，测试数据用于测试所训练的学习器的泛化能力。

极限学习机有两个比较重要的参数。一个参数是隐藏层单元个数，该参数决定了学习器的复杂度，隐藏层单元个数越多，学习器的复杂度就越高，也就能更有效地捕捉数据所蕴含的信息；但隐藏层单元数越多，就越容易受噪声的影响，从而增加过拟合的风险。如图4所示，可以看出随着隐藏层单元个数的增加，训练集和测试集的精度不断增高，但增高的幅度越来越小，综合考虑计算机运算性能和试验精度，本文选取900作为隐藏层单元个数。另一个参数是极限学习机的正则化项系数λ，该参数可以降低模型的过拟合程度。但从图4中可以看出学习器并没有发生过拟合，所以λ设置为0.000 1。本文选用的驱动因子有12个，目标变量是取值为0或1的二值变量，由此确定极限学习机的网络结构是输入层为12个单元，隐藏层900个单元，输出层1个单元，正则化系数λ设置为0.000 1。

图4 隐层单元个数与精度的关系Fig.4 Relationship between number of hidden layer units and accuracy

作为对比，本文也用同一批数据对逻辑回归和神经网络(单隐层)进行训练。表2是各学习器在训练集上耗费的训练时间以及在测试集上的总体精度和AUC指标。从训练时间可以看出逻辑回归的平均用时最短，因为其模型的复杂度最低，而极限学习机的训练时间明显低于同为单隐层的神经网络，体现了极限学习机在训练速度上的优越性。从整体精度上来看，极限学习机也要好于逻辑回归和神经网络。相比于逻辑回归，极限学习机将输入数据映射到高维特征空间中，解决了线性不可分的问题，从而可以学习更复杂的函数，而逻辑回归是线性分类器，在面对复杂的数据关系时表现不好；相比于神经网络，极限学习机可以化简为求解一个线性系统，从而求出全局最优唯一解，而神经网络是基于梯度下降算法迭代求解，不仅训练时间长，而且可能陷入局部最优解，要得出满意的解需要做更多的尝试。

表2极限学习机、逻辑回归和神经网络的训练耗时及在测试集上的总体精度和AUC指标

Tab.2Extremelearningmachine,logisticregressionandneuralnetworktrainingtime-consumingandoverallaccuracyandAUCindicatorsontestsets

参数极限学习机神经网络逻辑回归训练耗时/s376.81168.4254.5总体精度0.82050.79240.7339AUC0.90340.85300.8164

极限学习机、逻辑回归和神经网络会为每个测试样本产生一个实值概率预测，这个实值概率预测的好坏，直接决定了学习器的泛化性能，ROC曲线根据实值概率预测的结果，将测试样本进行排序，预测概率值最高的排在前面，概率值低的排在后面，排序本身质量的好坏，体现了综合考虑学习器在不同任务下“期望泛化性能”的好坏。AUC(area under ROC curve)是衡量不同学习器ROC曲线质量的一个重要指标，因此本文用AUC衡量不同学习器的泛化能力。图5即为不同学习器的ROC曲线及其对应的AUC值，可以看出极限学习机的AUC指标高于逻辑回归和神经网络。

图5 极限学习机、逻辑回归和神经网络在测试集上的ROC曲线及对应的AUC指标Fig.5 Extreme learning machine, logistic regression and neural network ROC curves on test sets and corresponding AUC indicators

上述试验是在样本较多的情况下进行的，作为对比，采用小样本数据(上述试验样本数量的1/3)以和上述相同的方法进行试验，试验结果表明极限学习机的测试精度为0.798 4，逻辑回归为0.718 1，神经网络为0.720 4，说明了极限学习机在小样本的情况下仍然具有较高的精度，而神经网络的性能却大幅下降，具体情况见表3。

表3小样本情况下不同学习器在测试集上的总体精度和AUC指标

Tab.3OverallaccuracyandAUCindicatorsofdifferentlearnersonthetestsetinsmallsamplecases

参数极限学习机神经网络逻辑回归总体精度0.79480.72040.7181AUC0.87700.80680.8034

2.4 城市扩展模拟与预测

使用ELM-CA做城市扩展的模拟时，首先利用训练好的极限学习机学习器求出试验区每个元胞转化潜力，在此基础上根据式(6)计算出元胞受邻域影响和随机因素影响的综合转化概率，模拟以2006年遥感影像分类数据作为初始状态开始循环迭代，每轮迭代中选取综合概率最大的前若干个元胞转化，每轮迭代后由于城市用地发生变化，需要重新计算邻域影响。当模型转换量达到实际2006—2010年间的城市转换总量时，则停止迭代，输出结果见图6。

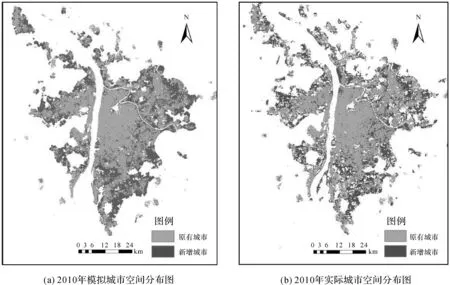
图6 2010年模拟城市空间分布图与实际城市空间分布图Fig.6 Simulated urban spatial distribution map and actual urban spatial distribution map in 2010

作为检验，根据从2006—2010年提取的转换规则，以2006年作为起始年份，预测2010—2013年间的城市扩展。当模型转换量达到实际2006—2013年间的城市转换总量时，则停止迭代，输出结果见图7。

图7 2013年模拟城市空间分布图与实际城市空间分布图Fig.7 Simulated urban spatial distribution map and actual urban spatial distribution map in 2013

2.5 模型检验与对比

城市扩展模型检验的方法有两种，一种是逐点对比的方法，即将模拟的结果与实际的图层叠加，逐点对比计算模拟的精度，假设2006年到2010年实际新增城市用地元胞个数为Q，模拟的新增城市元胞与实际新增城市元胞在空间上位置一致的元胞个数为S，即正确模拟元胞数为S，则精度P=S/Q，这里只讨论城市的模拟精度；另一种是整体比较，即比较模拟结果的空间格局与实际的空间格局的符合程度，这里使用Kappa系数。

为了进一步的验证模型，用逻辑回归和神经网络模拟同一地区2006—2010年时间段的城市扩展。将从遥感影像解译得到的实际用地与极限学习机、逻辑回归与神经网络的模拟结果进行比较，得到混淆矩阵表4，从表中可以看出，极限学习机模型的城市模拟精度70.30%，Kappa系数0.669 7，Logistic模型的城市模拟精度68.09%，Kappa系数0.645 0，神经网络模型的城市模拟精度68.76%，Kappa系数0.652 8。极限学习机模型相比于逻辑回归和神经网络，城市模拟精度分别提高了2.21%和1.54%，说明极限学习机模型有更好的精度，而Kappa系数分别提高了0.024 7和0.016 9，说明ELM模型模拟结果与实际城市拥有更好的一致性。同时进一步的比较了不同模型的FoM(Figure of Merit)系数，ELM模型的FoM系数为0.542 1，分别比Logistic(0.516 2)模型和神经网络(0.524 2)模型分别提高了0.025 9和0.017 9，说明了ELM模型拥有更好的模拟能力。FoM系数的计算公式如下

(10)

式中，A为实际中发生转化但模拟中没发生转化的错误区域面积；B为实际中和模拟中都发生转化的正确区域面积；C为实际中未发生转化但模拟中发生转化的错误区域面积。

本文增加了2006—2013年时间段的城市扩展预测，来检验模型的有效性。根据2006—2010年时间段提取的转换规则，以2006年土地利用为初始状态，预测2010—2013年城市扩展，将预测结果与实际用地比较，得到混淆矩阵见表4，极限学习机模型的城市预测精度分别高于逻辑回归和神经网络模型1.87%和1.2%，Kappa系数分别高于逻辑回归和神经网络模型0.023 3和0.015 9，FoM系数分别提高了0.022 2和0.015 7，证实了极限学习机模型的可靠性。

表4 极限学习机、逻辑回归和神经网络模拟结果的混淆矩阵

试验的结果与2.3节中的对学习器的精度评价一致。值得指出的是，本文在模拟城市扩展过程中，每次迭代会选择本轮中综合转化概率最高的前若干个元胞转化为城市用地，因此，城市扩展模拟结果的好坏高度依赖于学习器给出的预测概率的排序的好坏，在图5中可以看出极限学习机的ROC曲线的AUC值明显高于逻辑回归和神经网络，而模拟试验的结果也验证了这一观点。

另外，本文也计算了实际结果与模拟结果的形态指数，以检验模拟结果与实际情况空间格局的一致性。本文采用Moran I指数反映试验结果的空间聚集与分散程度，计算结果见表5。从表中可以看出，极限学习机的试验结果的Moran I指数较逻辑回归和神经网络更接近于实际值，这说明极限学习机模型模拟结果的空间格局都与实际情况比较接近。

表5 Moran I指数对比

为了考察样本数据量大小对模拟结果的影响，利用在2.3节中在小样本情况下训练的不同模型，分别对2010年和2013年的城市用地进行模拟和预测，试验结果见表6。

表6小样本情况下不同学习器的性能表现

Tab.6Performanceofdifferentlearnersinsmallsamplecases

年份参数极限学习机逻辑回归神经网络2006—2010年精度0.68640.62790.6270Kappa0.65110.58610.5851FoM0.52250.45760.45662006—2013年精度0.68450.62870.6035Kappa0.61180.54310.5130FoM0.52040.45850.4321

在2006—2010年的城市扩张模拟中，小样本相比于大样本的情况下，极限学习机模拟精度、Kappa系数和FoM系数分别下降了1.6%、0.018 6、0.001 6，而逻辑回归和神经网络分别下降了5.3%、0.058 9、0.058 6和6.09%、0.067 7、0.067 6(表4、6)。

在2006—2013年的城市扩张预测中，极限学习机的预测精度、Kappa系数和FoM系数分别下降了1.75%、0.021 7、0.020 7，而逻辑回归和神经网络分别下降了5.46%、0.067 1、0.060 4和8.5%、0.104 8、0.093 9(表4、6)。

可以看出，样本数据量的大小对极限学习机的影响较小，逻辑回归次之，对神经网络的影响最大。因为神经网络的模型较为复杂，在数据量较少时容易发生过拟合，需要正则化机制来防止过拟合，而极限学习机算法内嵌良好的正则化机制，在样本较少时仍可以较好地工作。极限学习机的这一特点使其在样本较少或样本获取困难的情况下，仍然可以获取相对较高的模拟精度。

3 结论与讨论

(1) 本文提出的基于极限学习机的城市扩展元胞自动机模型(ELM-CA)，有效地简化了CA模型的复杂度，极限学习机通过历史数据训练得到CA的转化规则，减少了人为主观因素的影响，适合复杂的土地利用变化模拟，能够模拟出复杂的城市空间形态及其变化。

(2) 本文模型充分考虑了不同土地利用类型转换为城市用地的差异和强度，分别求出耕地、林地、水域三种主要用地类型所对应的转换参数，在获取中心元胞城市化潜力的时候，就用中心元胞用地类型对应的转换参数，这样就减小了用地类型的不同所带来的影响。

(3) 对比试验分析表明，ELM-CA模型的城市模拟精度和预测精度均高于逻辑回归和神经网络，能有效模拟与预测城市扩展的空间形态及其变化，而且ELM模型的训练时间仅为神经网络的1/3左右，体现了ELM学习速度快的优势。

(4) 对比大样本和小样本情况下不同学习器的性能表明：在小样本情况下，逻辑回归和神经网络的性能受到较大的影响，而极限学习机仍能保持较为良好的性能，使其在样本难以获取的情况下具有明显优势。

(5) 本文模拟过程分为两个阶段，第一阶段通过学习器对采样数据进行学习，获取驱动因子与城市发展潜藏的复杂关系，第二阶段利用训练好的学习器进行城市扩张模拟与预测。不难发现，虽然在第一阶段的样本数据学习中，极限学习机的性能表现明显好于逻辑回归和神经网络，但在第二阶段的城市扩张模拟与预测中，极限学习机的试验结果相对于逻辑回归和神经网络提高的并不显著。其中一个重要原因是，在第一阶段中，利用学习器对采样数据进行学习的时候并没有将空间关系考虑在内，而仅是在第二阶段的模拟与预测中，通过式(6)将空间相关性纳入模型中，这样会导致学习器并没有学习到样本数据中所蕴含的空间关系，而空间相关性在城市扩张中具有重要的影响，从而使得学习器在城市空间分布模拟与预测的表现有一定的折扣。所以在后续的研究中，将进一步试验直接利用学习器学习样本数据的空间相关性，以期使得试验方法更为科学，减少主观因素的影响。