基于理论分析与仿真验证的船用空压机平衡轴设计*

胡甫才 魏志威* 徐 阳 薛厚强 高 硕

(武汉理工大学高性能船舶技术教育部重点实验室 武汉 430063) (武汉理工大学能源与动力工程学院 武汉 430063)

0 引 言

往复式空气压缩机通过曲柄连杆机构将活塞的往复运动转变为曲轴的旋转运动，曲柄连杆活塞机构的运动会产生不平衡惯性力,从而产生振动[1]，这不仅会使运动部件产生磨损和疲劳破坏甚至断裂，降低设备的使用寿命，而且也会产生噪声污染，影响工作人员的健康.为了减小了空压机的激励力从而降低整机的振动，最终降低整机的噪声水平，提升舒适性和延长机器的使用寿命,本文以某船用往复式空压机为研究对象，从减小或消除空压机的振动源这一根本措施出发，以结构动力学分析为基础，设计平衡轴[2]机构，从而达到平衡空压机内部各种不平衡力(矩)的目的.

本文研究某船用往复式空压机的理论价值是通过ADAMS软件对结构振动进行仿真分析对比，权衡加装平衡轴机构的可行性与优缺点，对实践有一定指导意义.

1 空压机动力学分析与求解

本文研究的船用空压机的型号为CZ60/30，其运动部件的参数见表1.

表1 曲柄连杆机构材料的主要参数

由于连杆的运动方式较为复杂，根据等效质量分解法可简化运动部件达到简化动力学分析[3]的目的，可求出等效连杆小端质量为m1=1.52 kg；等效连杆大端质量为m2=4.10 kg.

1.1 惯性力求解

空压机中的惯性力[4]主要有两种，一种是曲柄和连杆大端做旋转运动的旋转惯性力；另一种是活塞组件和连杆小端直线来回运动产生的往复惯性力.

往复式空气压缩机的旋转惯性力由以下两方面构成，主要部分是曲柄旋转产生的惯性力；次要部分是连杆大端及一部分等效质量旋转产生的惯性力.

由牛顿力学离心力公式可求旋转惯性力为

Fx=mxrxω2=mqrqω2+m2rω2=1 452.68 N

(1)

式中:mq为曲轴质量；m2为等效连杆大端质量；rq为曲轴的旋转半径.

往复惯性[5]力大小跟往复运动的部件产生的加速度a大小成正比，且具有相反的方向，根据牛顿第二定律F=ma，得出其计算公式为

Fw=-ma=-(mh+mx+m1)×

rω2(cos (ωt)+λcos 2 (ωt))

(2)

式中：mh为活塞组件质量；mx为活塞销质量；m1为等效连杆小端质量；r为曲柄半径；a为加速度；λ为连杆比；ω为曲柄角速度，根据ω=2πn，(h为曲轴转速)n取750 r/min.

以上公式中包含前两阶的往复惯性力，忽略了高阶的往复惯性力.两阶往复惯性力可分解为

一阶往复惯性力：

FwⅠ=-(mh+mx+m1)×

rω2cos (ωt)=FⅠcos (ωt)

(3)

二阶往复惯性力：

FwⅡ=-(mh+mx+m1)r×

ω2λcos2 (ωt)=FⅡcos2 (ωt)

(4)

式中：FⅠ为一阶往复惯性力幅值大小；FⅡ为二阶往复惯性力的幅值大小；代入各已知参数的数据分别计算得到FⅠ=-2 698.09 N；FⅡ=-562.01 N.

由于曲轴箱大小的限制，无法同时平衡两阶往复惯性力，一阶的力占总往复惯性力的80%以上，因此，文中只研究平衡一阶往复惯性力.

1.2 气体作用力

往复式空气压缩机CZ60/30的气体力[6]除了作用在活塞顶部外，还对活塞底部有作用力，即存在低压级和高压级的气体压力.根据气体力计算公式，将高压级和低压级气体力合并可得到气体力随时间变化的曲线图，见图1.

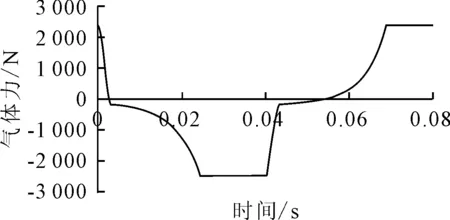
图1 气体力变化曲线图

1.3 倾覆力矩计算

由于活塞组件产生的往复惯性力及气体力对气缸和连杆施加力，使其产生的侧推力对曲柄旋转中产生倾覆力矩和沿连杆的分力对曲柄旋转中心产生转矩.曲柄连杆机构受力分析图见图2.

图2 曲柄连杆机构受力分析图

作用在活塞上面的力F主要有气体力和惯性力，通过连杆力的传递作用，在A处把力F分解为两个侧推力，再在B点分解侧推力，指向圆心的力不产生力矩，与圆相切的力产生力矩.根据力矩公式得到倾覆力矩T的计算公式为

T=FcX=Ftanβ(rcos (ωt)+lcosβ)=

(5)

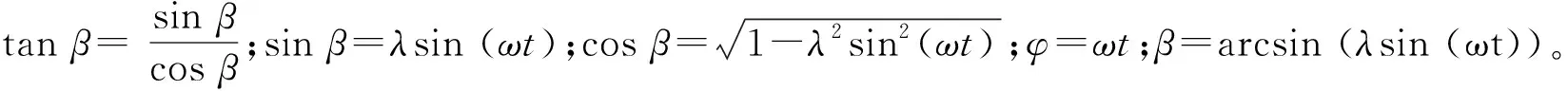
2 平衡轴设计

2.1 平衡轴参数计算

首先假设两根平衡轴的位置、质量和质心旋转半径一致，由于双平衡轴的旋转方向相反[7-8]，两根平衡轴水平方向的旋转惯性力相互抵消，垂直方向分力相互叠加用来平衡一阶往复惯性力.图3为双轴平衡轴的受力分解图，根据算得的一阶往复惯性力的幅值为2 698.09 N，可以计算一根平衡轴在竖直方向需平衡的惯性力为

m1)rω2=-1 349.05 N

(6)

图3 双轴平衡轴受力分解图

由于曲轴没有采用过量平衡法，连杆等效大端质量旋转运动形成的惯性力无法平衡，因此两根平衡轴参数相同不可行，要额外考虑连杆等效大端质量旋转惯性力，需要在其中一根平衡轴增加部分质量，此部分旋转惯性力为

FE=mrω2=mqrqω2+m2rω2=1 452.68 N

(7)

因此，两根平衡轴大小不相同，其旋转惯性力为

Fx=mxrxω2=1 349.05 N

(8)

Fd=mdrdω2=FY+FE=2 801.73 N

(9)

式中：Fd为大平衡轴旋转惯性力；Fx为小平衡轴旋转惯性力；md为大平衡轴质量；mx为小平衡轴质量；rd为大轴旋转半径，rx为小平衡轴旋转半径.

通过UG软件建立初步的三维模型，根据平衡轴旋转惯性力的大小，采用实体分析模块计算出实体的体积、回转半径、质心和旋转惯性力等参数，从而得到平衡轴的实体参数见表2.

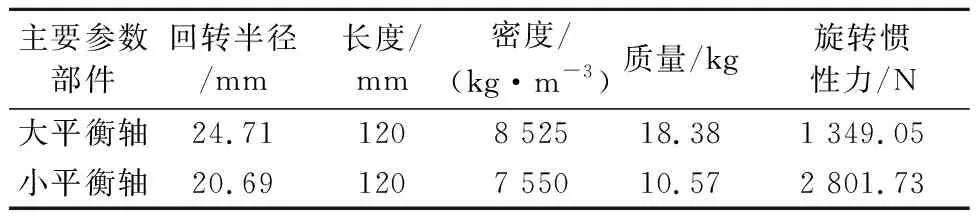
表2 大小平衡轴的主要参数

2.2 平衡轴位置分析

在平衡轴布置时，要达到既可以平衡一阶往复惯性力和旋转惯性力，又能平衡部分倾覆力矩的效果.由1.3的计算表明，倾覆力矩不是标准的正弦或余弦函数，是由正余弦函数相加和相乘得到的非标准周期函数形式，而平衡轴产生的力矩是周期的正弦或余弦函数形式，两者不能完全抵消，只能采用理论计算，寻找最佳的平衡轴位置.

经对比分析，本文采用粗细双轴平衡机构对称布置方式为最佳.图4为粗细双平衡轴机构对称布置示意图，由图4可知，两根平衡轴是对称布置但大小不一样，产生的旋转惯性力大小也不同，且旋转方向相反.根据受力分解，在Y轴方向的分力是同向相叠加，效果是与一阶往复惯性力相抵消；虽然力臂大小相同，但正因为力的大小不同，对机体而言，两者对O点的力矩相叠加成附加力矩；在X轴方向的力大小和方向不一致，效果是部分相抵消且会在X轴方向产生附加的不平衡力，虽然力臂大小一致，但最终在X轴方向也会产生附加力矩.通过合理调整平衡轴的安装位置，使其在X轴和Y轴方向产生的力矩大小不同，形成一个合力矩，最终平衡部分倾覆力矩.

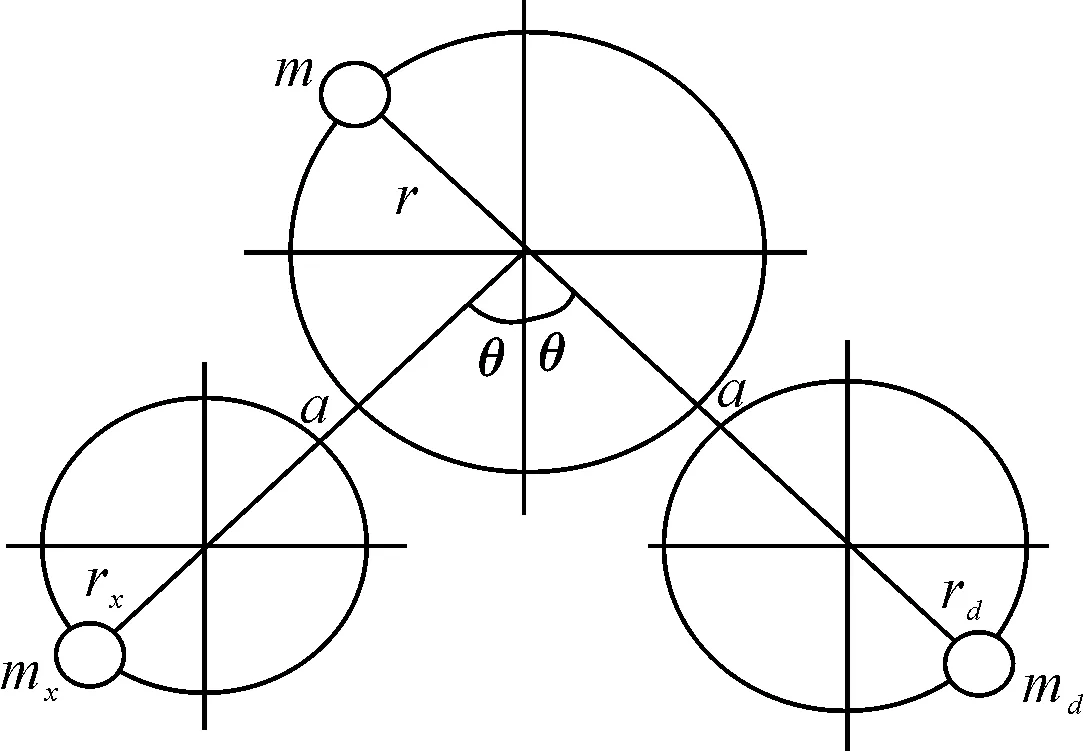
图4 粗细双平衡轴机构对称布置示意图

2.3 倾覆力矩对比分析

气体力和活塞组件的往复惯性力的水平分力均可以产生倾覆力矩，1.3中推导出了倾覆力矩的计算公式.通过Matlab编程画出活塞组件的往复惯性力和气体力的合力及倾覆力矩的曲线见图5.

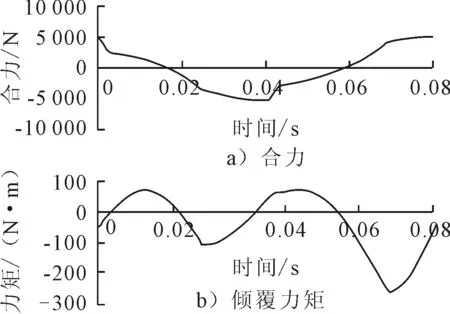
图5 往复惯性力和气体时域图

加装平衡轴前后倾覆力矩的时域图见图6.

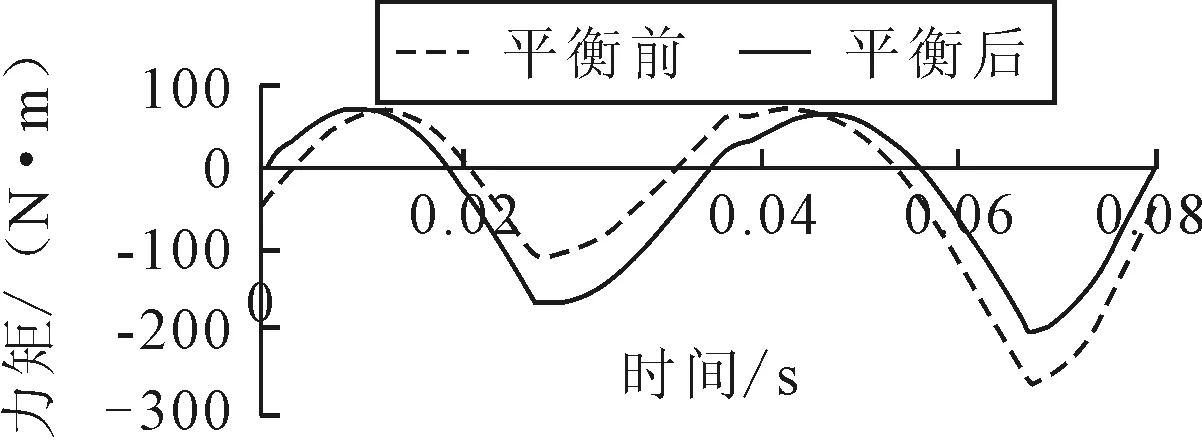
图6 平衡前后倾覆力矩对比时域图

由图6可知，上述方法可以平衡部分倾覆力矩，由于有效平衡倾覆力矩是建立在平衡二阶往复惯性力上的，而本文设计的目的是平衡一阶惯性力且能部分平衡倾覆力矩，已经达到了设计的初衷.

3 空压机动力学仿真分析

首先，使用UG软件对CZ60/30空气压缩机和平衡轴机构进行三维建模.使用ADAMS软件对空压机模型进行多刚体动力学仿真[9-10]，其目的是验证运动部件的往复惯性力和旋转惯性力的理论计算的正确性及加装平衡轴的效果.对仿真模型设置驱动转速为750 r/min，周期0.08 s，步长800步，在去除重力影响的前提条件下，大小平衡轴和曲轴的仿真结果见图7.

图7 Y方向旋转惯性力曲线

由图7可知，大小平衡轴和曲轴各自两端的惯性力在Y方向上的变化规律是一致的，图中也求出了轴两端的合力在Y方向上的变化，从而可以得到惯性力的仿真值与理论计算值的对比，见表3.

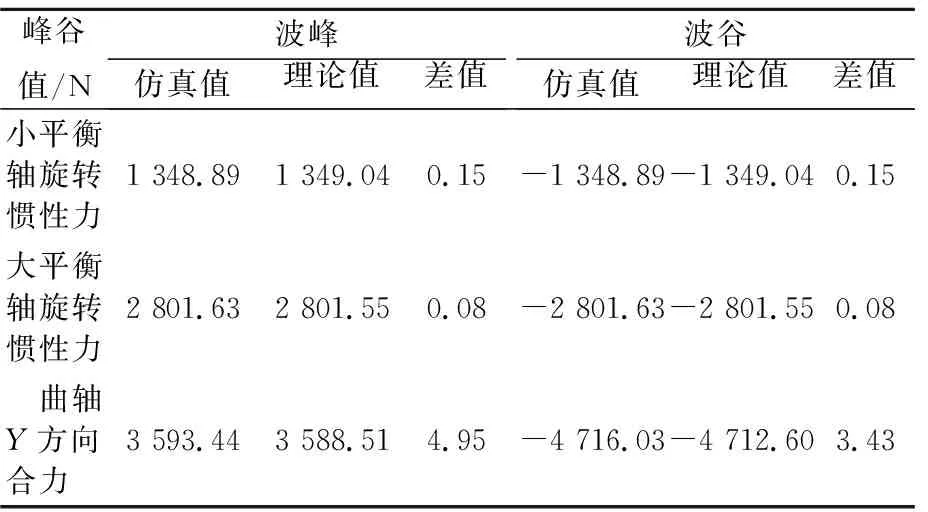
表3 惯性力极值对比

由表3可知，仿真值与理论计算值的波峰与波谷值几乎一致，误差小于0.01%.因此，有理由认为多刚体动力学仿真过程和理论计算均合理正确.图8为空压机Y方向惯性力曲线图.

由图8可知，以正向为起点的点画线为大小平衡轴在Y方向的旋转惯性力合力曲线，以负向为起点的实曲线是曲轴轴承在Y方向的惯性力曲线，中间的点画曲线是两者合力曲线.图8可以清晰的看出平衡轴对曲轴惯性力的平衡作用.表4为加装平衡轴后的仿真合力与曲轴惯性力的极值对比，可以得到，在Y方向的激励力峰谷差值从8 309.77 N减小为1 196.64 N，理论上能有效平衡了85.60%的Y方向的激励力.因此，根据仿真结果与理论计算的一致性，充分验证了平衡轴的参数理论计算与模型设计均合理正确，能有效平衡整机竖直方向的激励力.

表4 合力极值对比

4 空压机瞬态响应分析

通过平衡轴的设计计算，理论上平衡了较大部分不平衡力和力矩，有效减小了机体内部产生的激励力，从而达到减弱振动的目的.采用瞬态响应分析方法，重点分析机体位移，对比有无平衡轴对空压机结构瞬态响应的优化效果.

本文使用MSC Patran&Nastran软件进行瞬态响应分析[11]，在空压机的实体模型和有限元模型建立之后，定义材料属性，对有限元模型施加边界条件并加载激励力，然后进行计算.选取振动最复杂的缸盖顶部中心节点的Y方向的位移时域图进行分析，见图9.

图9 节点在Y轴方向的位移时域图

由图9可知，加装平衡轴前后其位移幅值变化较大，幅值范围从-0.6～0.8 mm变为-0.31～0.49 mm，且加装平衡轴后曲线变化规律较为平缓.根据振动瞬态响应位移时域图对比分析结果可知，机体的位移与受力变化趋势具有一致性特点，通过平衡轴的平衡作用，能有效平衡空压机机体内部产生的不平衡力和力矩，达到优化机体振动动态特性的目的.

5 结 论

1) 使用ADAMS软件进行动力学仿真计算，对比理论与仿真计算得到的惯性力值，误差在0.01%以内，验证了动力学仿真过程和理论计算均合理正确.

2) 对比仿真计算得到的加装平衡轴前后空压机惯性力的值，理论上能有效平衡了85.60%的Y轴方向的惯性力，有充分理由说明平衡轴的参数理论计算与模型设计均合理正确，能有效平衡Y方向的激励力.

3) 选取缸盖中心节点做瞬态响应分析，对比此节点加装平衡轴前后Y方向位移，有大幅度减小，证明通过平衡轴的平衡作用，能有效平衡空压机机体内部产生的不平衡力和力矩，达到优化机体振动动态特性的目标.